NSGA-Ⅱ算法与能量法相结合的舰艇居住舱室布局优化研究

冯青，张承嫄，余隋怀，陈登凯

（1.西安科技大学，西安 710054；2.西北工业大学 现代设计与集成制造技术教育部重点实验室，西安 710072）

舰艇设计具有其特殊性及复杂性，随着智能设计的发展，智能化的布局优化方法已经渗透到船舶设计的各个领域，从舱室整体划分到管道布局都有所涉及[1-3]。舰艇居住舱室作为士兵生活娱乐的主要场所，属具合理的空间布局决定着船员生活休息状态，其布局优化研究也显得尤为重要。

目前对于布局问题的求解，主要应用的方法有遗传算法[4]、粒子群算法[5]、鲁棒优化等[6]。如王运龙等[7]将能量法与遗传算法结合求解客舱室内布局。熊炳旭[8]结合模拟退火算法和遗传算法求解，缩小了局部最优解范围。随着遗传算法研究的深入，部分学者也将改进遗传算法应用于布局研究，突破传统遗传算法壁垒，如应用多目标遗传算法求解载人潜水器舱内布局[9,10]、电动牵引车总成布局[11]等。但针对舰艇居住舱室布局优化的研究尚少，方法创新性低，制约舰艇整体设计效率的提升。

现阶段针对舰艇居住舱室内部布局优化的研究尚存在以下问题：1）居住舱室内的布局研究多仅限于邮轮豪华舱室、作业舱室等。针对舰艇居住舱室的研究较少，如何考虑其特殊性，将自动化的布局设计方法应用于舰艇居住舱室设计，还有待深入。2）目前对舱室布局问题求解多应用传统遗传算法，在编码方式和选择运算上都存在一定的局限性，限制了运算速度，整体求解过程自动化程度低，且对多目标优化问题存在求解困难。本文综合考量了舰艇居住舱室的特殊性，提出一种结合能量法与NSGA-Ⅱ算法的求解方法，量化舰艇布局中的特殊需求，简化计算方式，并实现方案的自动布局及优选。

1 结合能量法的NSGA-Ⅱ算法设计

舰艇室内布局设计相对于普通居住环境更为复杂，由于舰艇的外板线型、舱室总体布局划分、结构层高，房间中风、管、电走向的影响，船上居住舱室普遍具有整体空间低矮、狭窄、密闭等特点[12]。如图1所示。

图1 某舰艇士兵居住舱室实景图Fig.1 Real picture of the living quarters of soldiers on a ship

舱室内属具摆放遵循特定的规则，如船舶居住舱室中的属具设备一般都是紧贴舱室四壁进行布置的，这样可以有效地利用舱室空间，不会显得舱室狭小，令居住人员心情舒畅[13]。床铺需布置在靠船舷一侧，方向与船长一致，保证船员的睡眠舒适性。为满足布局优化中属具摆放的特殊要求，本文采用能量法的思想对待布空间进行数学模型量化。

1.1 能量法量化舱室布局规则

能量法原是固体力学中的一种方法，是功与能量相关方法的统称，通过能量的叠加与转化来解决弹性构件的静力学问题[14]。能量法方程固定，形式统一，更适用于计算机编程计算。在舱室布局优化中，借助能量法在思想，结合人工势场法[15]，将待布空间划分为若干个能量区域，根据适宜布置属具的程度为区域赋予能量值，最终通过对比属具覆盖区域能量值和的大小筛选方案。

由于舰船居住舱室中属具大都紧贴舱壁进行布置，在建立舱室能量空间时，可以通过对舱室四壁赋值建立舱室数学模型。赋值的大小反应舱壁适宜布置属具的程度，当属具紧贴舱壁布置即可获得能量值。图2以某空间为例说明能量法的赋值计算过程。

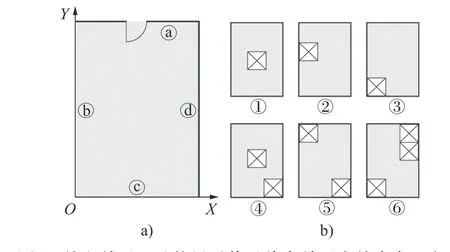
图2 舱室单元四壁能量赋值及待布单元在舱内布置方案Fig.2 Energy assignment of four walls of cabin unit and arrangement scheme of unit to be distributed in cabin

图2 a）依据布置需求为待布空间四壁赋予a、b、c、d这4个能量值，属具紧贴舱壁布置即可获得对应的能量值，未贴舱壁布置则能量值为0。图2 b）中①～⑥布局方案表示了待布单元在舱室中的布置情况。待布单元即需要布置的属具，如床铺，桌椅，衣柜等。这些属具设备一般为不规则图形，为方便计算，且考虑到设备的功能要求和使用人员舒适度，为待布置的属具设备建立姿态空间[7]，即包含实现使用功能的属具空间。姿态空间相较于原有属具单元更大，一般几何化为矩形进行计算。例如④方案表示舱内有两个待布单元，一个不贴四壁，一个贴合两个舱壁，以此类推。方案①到⑥获得的总能量值的大小为待布单元贴合舱壁数量对应能量值的叠加，各方案具体获得能量值见表1。

表1 舱室单元能量值求解Tab.1 The energy value of the cabin unit is solved

在为舰艇舱壁赋值过程中，需综合考虑舱室人员中心活动区域，动线及门等特殊单元的位置。图2中Y轴为船长方向，指向船首，X轴为船宽方向，指向船舷。因床铺需沿船长方向布置，Y轴赋值普遍高于X轴。由于门等固定单元的限制，有门的一侧赋值低于没有门的一侧，依据以上舱室布局需求，图2舱壁赋值大小关系为b=d>c>a。为方便计算，a、b、c、d的取值以舱壁数量而定，一般取10以内的整数，按适宜布置程度呈依次递减。本例舱室有四面舱壁，a、b、c、d可取1～4的整数进行计算。依据能量法量化待布舱室布局规则，建立NSGA-Ⅱ算法中的目标函数。

1.2 NSGA-Ⅱ算法求解布局问题

布局问题的研究起始于1831年Gauss 对“格（Lattice）”装填布局问题的研究，在理论上是属于切段装填问题和约束满足问题[16]。舰艇居住舱室布局设计属于布局优化中的装填问题，即在给定的舱室空间中对属具设备进行随机排布。其布局约束主要处理待布空间内待布物体的摆放及物体间的相互关系问题。求解过程中以一种形式化的符号描述待布舱室及待布属具，经过数学模型计算后再转化为布局方案输出，布局求解属于多项式复杂程度的非确定性问题（Non-deterministic polynomial，NP）问题，遗传算法在其中应用广泛。

遗传算法[17]是一种基于生物遗传和进化机制的随机搜索算法，具有较强的全局搜索能力，适用于解决复杂系统优化问题，缺点是运行速度较慢，且容易受参数的影响[18]。布局问题往往涉及多目标求解，即优化目标在两个及以上的遗传算法。以最大化目标值为例，设有n个决策变量，m个目标变量，以及多个约束条件。多目标遗传算法优化模型可描述为[19]：

式中：F(x) 为目标函数；x为维数为n的决策变量，构成决策空间；fm(x) 为维数为m的目标变量，构成目标空间；gj(x)为维数为j的不等式约束；hk(x)为维数为k的等式约束。

NSGA-Ⅱ算法是基于Pareto 改进的多目标遗传算法，2000年由Deb 等人提出，相较于在传统遗传算法在运算速度和算法鲁棒性得到进一步提高[20]，计算复杂度降低。NSGA-Ⅱ算法在选择操作中加入了精英策略，使父代中的优秀个体保留在子代，保证最优解不被淘汰。并采用了拥挤度的概念，通过判断同一非支配层中个体周围的拥挤程度，改善同一支配层面的种群多样性，在全局搜索上优于传统遗传算法算法[21]。NSGA-Ⅱ算法求解多目标优化问题的基本运算流程为：对随机产生初始种群N 进行非劣（Pareto）前沿分级，通过交叉变异得到新一代种群（父级与子集合并的种群）；再次通过Pareto 前沿分级并进行拥挤度计算，选择合适个体组成新种群后进行交叉变异；以此类推，直到最优解产生。

1.3 算法的实现流程

基于能量法的NSGA-Ⅱ算法求解舰艇居住舱室布局流程如图3所示。输入待布空间和待布属具的基本参数，即明确待布空间的大小和方向，待布属具的姿态空间大小；再利用能量法对待布空间的四壁赋值，准备运算；依据遗传算法编码方式进行编码，进入NSGA-Ⅱ算法流程求解最优解；得到Pareto最优解集后选取点并将其转化为布局方案并输出；经方案筛选与评价，如不符合需求则返回Pareto 最优解集进行重新选择；得到满意的方案后，还需经人工调整，输出最优布局。

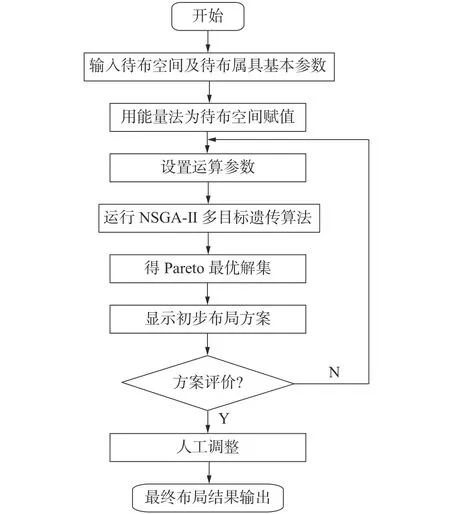
图3 NSGA-Ⅱ算法实现流程图Fig.3 NSGA-Ⅱ algorithm implementation flow chart

2 居住舱室布局优化模型构建

在进行二维平面的舱室布置计算时，需对待布空间和待布属具建立数学模型。能量法确定待布舱室四壁的能量值，待布空间经姿态空间计算后简化为矩形单元进入算法流程，NSGA-Ⅱ具体算法设计如下：

1）设计变量

布局设计主要是对属具单元在空间中的位置进行排列组合，因此，选择待布属具中心点位置坐标作为位置参数Xi(i=1,2,···,n)进行计算，即

式中：xi为待布单元i中心点的x坐标；yi为待布单元i中心点的y坐标；n为待布单元的数量。

2）目标函数

（1）多人士兵舱室中，人员活动干扰较大。为保证舱室内人员活动空间错开，动线产生的干扰较小，同一类型的属具之间距离越远越好，用F1(X)来描述，越大越好，在运算过程中求解最大值。

式中：mi为待布单元优先布置权系数，按属具排布的重要度赋值。赋值以属具种类数量而定，10以下为宜。

（2）中心活动区域是属具摆放后的剩余空间，因属具摆放占地面积一定，剩余空间面积也固定。但剩余空间是否具有整体性，方便人员活动，还需判断。为保证舱室布置中心活动区域最大，用F2(X)表示各属具中心点到舱室中心点的距离之和，F2(X)越大越好。在运算过程中该目标函数求解最大值。

式中Xa为活动区中心点位置参数

（3）能量法对属具单元摆放的方向、位置进行了规范，为满足约束条件，待布属具所获整体能量值越大越好，此处用F3(X)表示。在运算过程中，求解最大值。

式中：exi为待布单元沿X轴的能量值；eyi为待布单元沿Y轴的能量值；si为待布单元沿X轴方向的长度；qi为待布单元沿Y轴方向的长度；L为待布空间沿X轴方向的长度；W为待布空间沿Y轴方向的长度；a,b,c,d为图2中四壁的能量值。

3）约束条件

建立舱室优化布置的约束条件时，主要考虑以下几类约束。

（1）属具布置不能超出舱室边界，即

（2）属具之间，彼此不干涉，即

3 实例验证

以某舰艇靠近船艏区域的两个20人居住舱室（居住舱A、居住舱B）为例进行布局优化设计，舱室布局如图4所示。利用MATLAB 编程软件对能量法改进的NSGA-Ⅱ算法进行验证，因居住舱靠近船艏，存在角度不大的斜面，为方便计算，将待布空间处理为矩形，如图5所示。

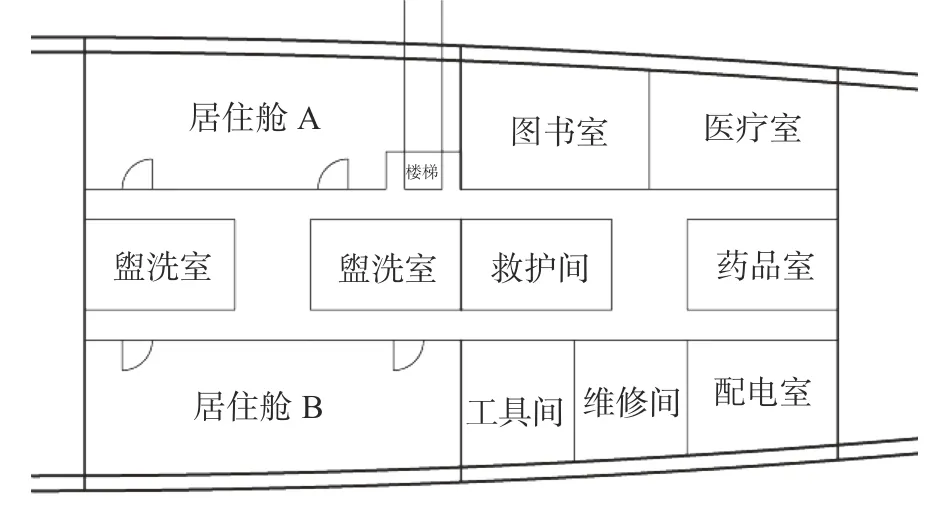
图4 船艏舱室能量值图Fig.4 Bow room energy value diagram

图5 居住舱室几何化图Fig.5 Geometric diagram of accommodation

舰艇士兵舱室的布局应满足相应规范及人机工程学原则，如床铺长度 ≥ 1 900 mm，宽度650 mm，单人床铺需配置照明灯及床帘。床铺之间无障碍宽度为76.2 cm。每10个人应当配备一张写字台。每个士兵需要配备不小于0.1 m3的储物空间等。依此规划舱室内待布属具（床、书桌、储物柜）的数量和大小，并对各类属具加入姿态空间处理，见表2。

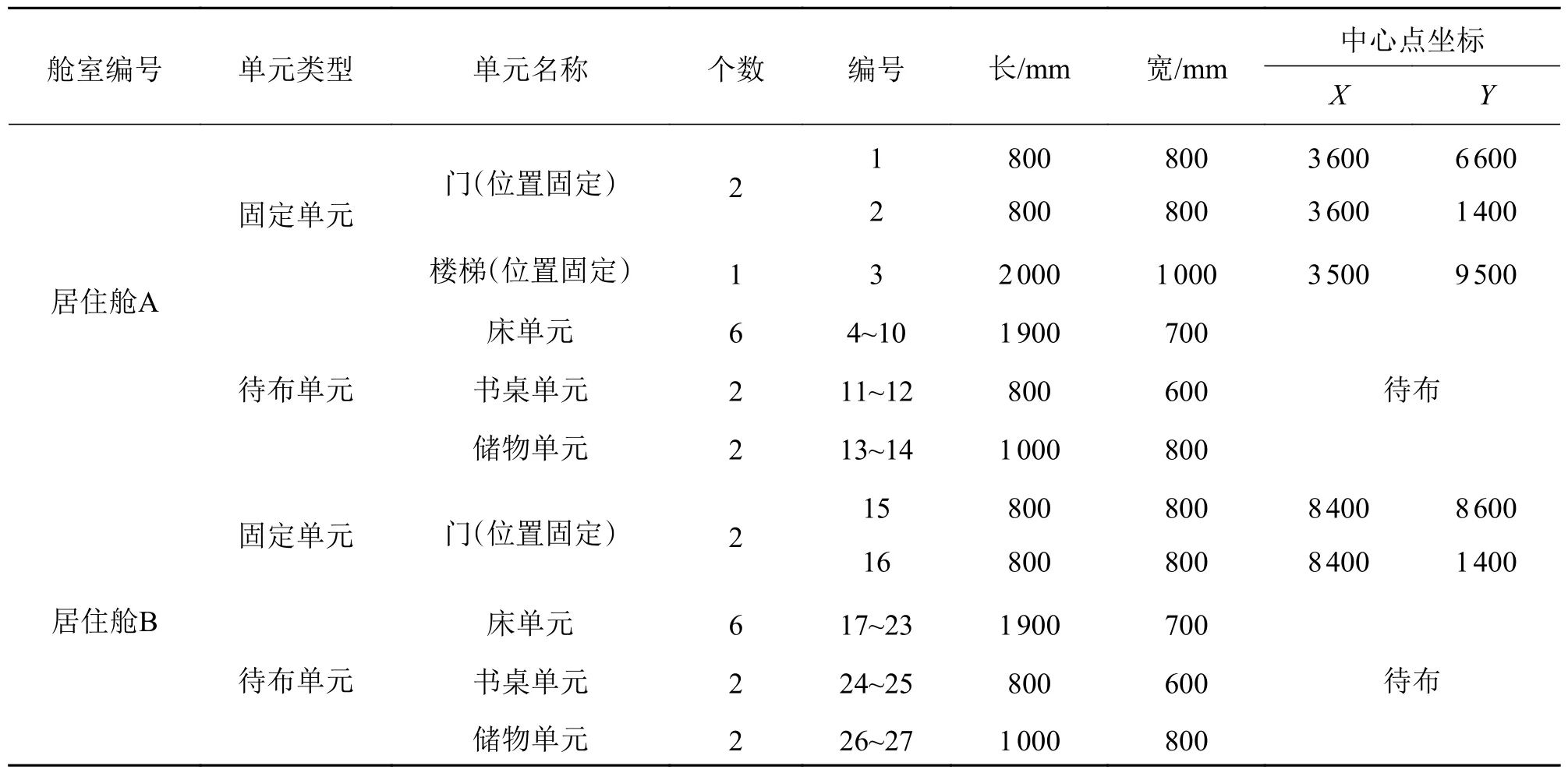
表2 待布舱室及待布单元数据Tab.2 Data of waiting room and waiting unit

待布空间平面图如图6所示，根据舰艇居住舱室设计的具体需求为舱壁赋值，适宜布置属具的舱壁赋值越大，反之则越小。图中Y轴沿船长方向，X轴指向船舷方向，因床铺应沿船长方向布置，门所在的舱壁不适宜布置过多属具，所以需确保Y轴的舱壁赋值大于X轴，无门一侧的赋值大于有门一侧的赋值。具体赋值见图6。运算过程中，满足F3(X)运算条件者即可获得能量值。

图6 待布舱室能量值图Fig.6 Energy value diagram of the room to be laid

运算过程中，以各待布属具的中心点为参数进行求解，si，qi取值由属具摆放方向和属具大小而定。因书桌单元和储物单元布置方向不确定，si，qi取值在计算中互换，进行两轮迭代。床单元布置方向需与船长保持一致，因此床单元取值固定，取si=1 900 mm，取qi=700 mm。门单元和楼梯单元因位置固定，所以在运算过程中固定赋值，具体取值见表2。参数设置好后随机赋值形成初始化种群，进入目标函数运算，即

式中：F1(X)为舱室内各类家具中心点的距离，越大越好；F2(X)为舱室中心活动区域的大小，越大越好；F3(X)为舱室内各属具摆放后获得的能量值和，越大越好；Xa为待布空间中心点，居住舱室A 取值为（2 000，5 000）；居住舱室B 取值为（10 000，5 000）；mi为待布属具的重要度，按士兵适用属具的频率进行重要度大小的赋值，在该舱室布局中，mi取值床单元 >储物单元 >书桌单元；取床单元mi=3，储物单元mi=2，书桌单元mi=1。

在NSGA-Ⅱ算法运算过程中，经过多种尝试，最终取种群规模50，迭代次数50，进行优化计算并得到Pareto 最优解集，最终输出47组解决方案，如图7所示。随机选取其中4个点位，验证算法有效性，表3以方案1为例显示具体数据输出数据结果。

表3 方案1布局优化结果Tab.3 Scheme 1 Layout optimization results

图7 舱室布局方案Pareto 最优解集Fig.7 Cabin layout scheme Pareto optimal solution set

依据图7选中方案，绘制初始舱室布局图，如图8所示。经过核定，该算法输出的布局方案符合舰艇设计要求。

图8 NSGA-Ⅱ输出方案Fig.8 NSGA-Ⅱ output scheme

因士兵舱室为多人居住空间，需要整体性较大的活动空间满足多人同时活动。现引入有效活动空间指标对输出方案进行筛选。有效活动空间是指舱内除去属具及属具周围无法利用的狭小空间后，所剩余的活动空间面积，具体计算公式为

式中：S为有效活动空间面积；A为室内空间总面积；S1为属具占用空间的面积；S2为无法利用的狭小空间占用的面积。

S2包括人员无法出入的空间面积及人员无法展开有效活动的空间面积。在实际计算过程中，可将待布空间用属具单元到舱壁的延长线进行划分，分区后判断区域空间可否被利用。4个方案具体划分情况如图8所示。空间能否被利用依据如下标准：1）进入子空间的宽度不小于800 mm；2）子空间对应地面面积不小于0.753 m2[22]。根据判断标准，4套方案的有效活动空间面积大小如图8阴影部分所示。

根据表4可知，方案2的有效活动空间最大。现选择方案2作为最终方案，建立三维模型，并通过计算机仿真设计绘制效果图[23]。方案2在设计过程中考量了舰艇士兵舱室布局中可能遇到的情况，结合船舱特点对靠墙的书桌单元进行组合设计，扩大中心活动区域。最终设计方案如图9所示。经评价，图9的最终设计方案符合舰艇士兵舱室设计需求，在小空间内最大限度的满足人员活动及空间利用。

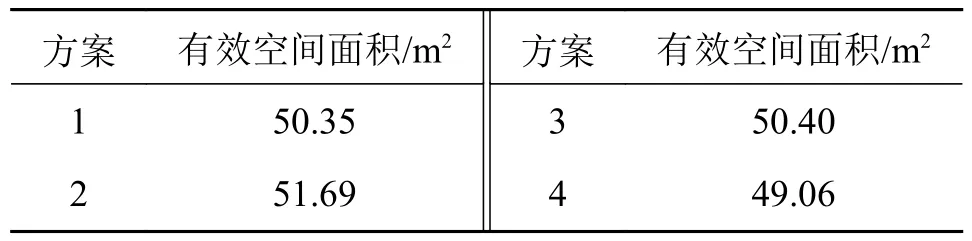
表4 方案有效活动空间计算Tab.4 Scheme active space calculation

图9 居住舱室最终效果图及细节展示图Fig.9 Living room final effect drawing and detail display drawing

4 结论

能量法将舰艇布局设计的原则量化，NSGA-Ⅱ算法拓宽设计的可能性，进行全局搜索并获取最优解，计算机将整套方法实现自动化，合理快速的实现空间布局优化，解放人力应用于更具有创造性的空间设计。现方法在求解同类复杂空间布局方面具有相对优势，但目前求解主要适用于二位平面布局的输出，对涉及高度的三维空间还需引入更多的参数进行迭代，且现阶段求解并未加入室内灯光、通风、人机工程学等相关因素的运算。因此，进一步优化工作的重点即是如何加入多因素的运算，并在算法求解过程中耦合多目标优化，获得符合设计原则的最优解集。