KLPP 特征约简与RELM 的高压隔膜泵单向阀故障诊断

李瑞，范玉刚，张光辉

（1.昆明理工大学 信息工程与自动化学院，昆明 650500；2.昆明理工大学 云南省人工智能重点实验室，昆明 650500）

高压隔膜泵是一种新型物料输送机械设备，具有性能稳定、密封性好和耐腐蚀等优点，已经广泛应用于精细化工、冶金铸造和废水处理等领域[1]。单向阀作为高压隔膜泵中核心的部件之一，需要在高负荷工况下保持连续运行，其工作状态直接影响高压隔膜泵的稳定性[2-3]。因此，对单向阀的故障诊断具有重要意义和价值。

振动信号能直接反映出机械设备所处的工作状态，对机械设备振动信号进行特征提取，用于构建表征其运行状态的特征集，是机械设备故障检测的关键[4]。励文艳等[5]将S 变换与奇异值分解结合提取柱塞式液压泵时频域特征，并采用极限学习机（Extreme learning machine，ELM）实现故障类型识别。孙岩等[6]通过短时傅里叶变换（Short-time fourier transform，STFT）提取轴承振动信号时频域特征，之后利用改进型胶囊网络（LR-capsulenet）实现对轴承的故障诊断。上述特征提取方法忽略了振动信号的时域和频域特征，难以全面表征设备的运行状态。时域、频域和时频域构成的多域特征集可以充分反映机械设备的运行状态，但多域特征集存在维数灾难等问题，易导致故障识别精度降低[7]。

流形学习是一种维数约简的有效方法，可用于对高维数据进行降维[8]。施莹等[9]通过等距映射方法，对轴承脉冲包络空间求解低维度本征包络特征，用于轴承的故障识别。张成等[10]使用局部保持投影（Locality preserving projection，LPP）流形学习方法对高维数据进行降维，减少数据中的离群点对加权k近邻规则（Weightedknearest neighbors，WKNN）模型故障识别结果的影响。刘长良等[11]引入核方法对LPP 算法进行非线性拓展，采用核局部保持投影（Kernel locality preserving projection，KLPP）方法，对高维数据进行降维。

以上文献表明高维特征集的低维流形结构能够表征设备的运行状态，用于构建故障诊断模型。极限学习机是一种有效的故障诊断模型，但ELM 在训练过程中存在隐层输出矩阵不稳定的问题[12]。正则化极限学习机（Regularized extreme learning machine，RELM）[13]通过引入正则项对输出权值范围进行控制，可有效克服ELM 模型过拟合导致泛化性能降低的问题。

运行状态表征提取和维数灾难等问题，降低了高压隔膜泵单向阀故障诊断模型的识别精度，为提升故障诊断模型的泛化性能和识别精度，本文提出一种基于KLPP 和RELM 的高压隔膜泵单向阀故障诊断方法。首先通过统计学方法[14]、傅里叶分析[15]和小波包分解[16]提取高压隔膜泵单向阀时域、频域和时频域特征组成多域特征集。之后利用KLPP 得到低维特征集，以表征高压隔膜泵的工作状态。最后建立基于RELM 的故障诊断模型，完成对高压隔膜泵单向阀运行状态的检测。

1 多域故障特征提取

1.1 时域特征提取

机械设备运行过程中产生的振动信号时域和频域特性会伴随着工作状态的改变而发生变化，分析相应特性的变化可以有效地识别出设备的工作状态[17]。对于给定的振动信号，利用统计学方法提取16个时域特征，并通过傅里叶分析提取13个频域特征参数。时、频域具体特征参数如表1与表2所示。x（n）表示振动信号序列，n=1,2,···,N，N为样本点数；s（k）表示x（n）的频谱，k=1,2,···,K，K为谱线数；fk为第k条谱线的频率值。时域特征中T1∼T10为有量纲时域特征统计参数，T11∼T16为无量纲时域特征统计参数。频域特征中F4∼F10描述频谱的分散或集中程度，F11∼F13描述主频位置的变化。

表1 时域特征Tab.1 Time-domain features

表2 频域特征Tab.2 frequency-domain features

1.2 时频域特征提取

不同状态的振动信号对各频率成分能量的抑制和加强效果不同，所以振动信号的频率成分能量中具有丰富的状态信息。小波包分解可以同时对低频和高频两个部分信号进行分解，而且这种分解既无冗余，也无疏漏，对含有丰富中、高频信息的信号可以比较好地实现时频分析，比传统的小波分解在时频域分析方法中更全面，对信号细节的分析效果更好[18]。本文通过小波包分解提取单向阀振动信号时频域能量和能量熵特征，从而与其故障类型之间建立映射关系。对于长度为N的振动信号x（n），小波包分解提取时频域信号特征步骤如下：

1）对x（n）作j层小波包信号分解，计算得到2j个子信号，并对第j层所有节点的信号作特征提取处理。小波包分解公式为

2）小波包分解系数经由j层低频到高频的频带得到，并通过迭代进行小波包分解系数重构为

式中：h和g为小波重构滤波器。

3）计算小波包频带能量。

式中：Ej,i为第j层i节点小波包分解系数能量；n为对应子信号的时间。则时频域信号能量特征为

4）由Shannon 熵[19]定义，计算第j层i节点的能量熵Hj,i为

式中：E为总能量；pj,i为第j层i节点在总能量中所占比重。则时频域信号能量熵特征为

2 核局部保持投影

核局部保持投影（KLPP）是一种对数据进行非线性降维的算法，数据映射到定义的核空间中构建邻域图，可以更好保存相邻数据之间的结构。设原始空间中的一组数据X={x1,x2,···,xn}经由定义的非线性映射投影到核空间 φ(xi)，i=1,2,···,n。核空间是一个高维空间。核空间中样本之间的点积是通过核函数K(xi,xj)计算得到的，核函数公式为

在高维空间运用LPP 算法，则

式中：D为对角矩阵；L=D-W，W是加权系数。其中，转换矩阵a为

式中v为系数向量。由式（8）与式（9）得

将式（7）代入式（10）得：

式（11）中，计算矩阵 (KDK)-1KLK的特征值相应的最小特征向量，组成转换矩阵。对于数据样本xtest，其投影为

3 正则化极限学习机

极限学习机（ELM）是一种单隐含层前向神经网络。ELM 模型参数的确定不需要经过复杂的迭代验证，直接计算就可以得到。但ELM 在训练过程中存在过拟合的问题。RELM 通过引入正则项，控制权值矩阵β的范数值，获得最小训练误差和输出权重。RELM 的目标函数为

式中：G（·）为激活函数；βi和wi为通过输出层、输入层分别和第i个隐含层神经元得到的权值向量；阈值bi通过第i层神经元得到，激活函数为g（∙）；C为正则化系数；ε为训练误差和。

通过目标函数构建Lagrange 方程为

对式（15）求偏导，得出权重矩阵为

式中I为单位矩阵。

因此，RELM 结果为

4 故障识别流程

KLPP 特征约简与RELM 的高压隔膜泵单向阀故障诊断研究方法流程图如图1所示。

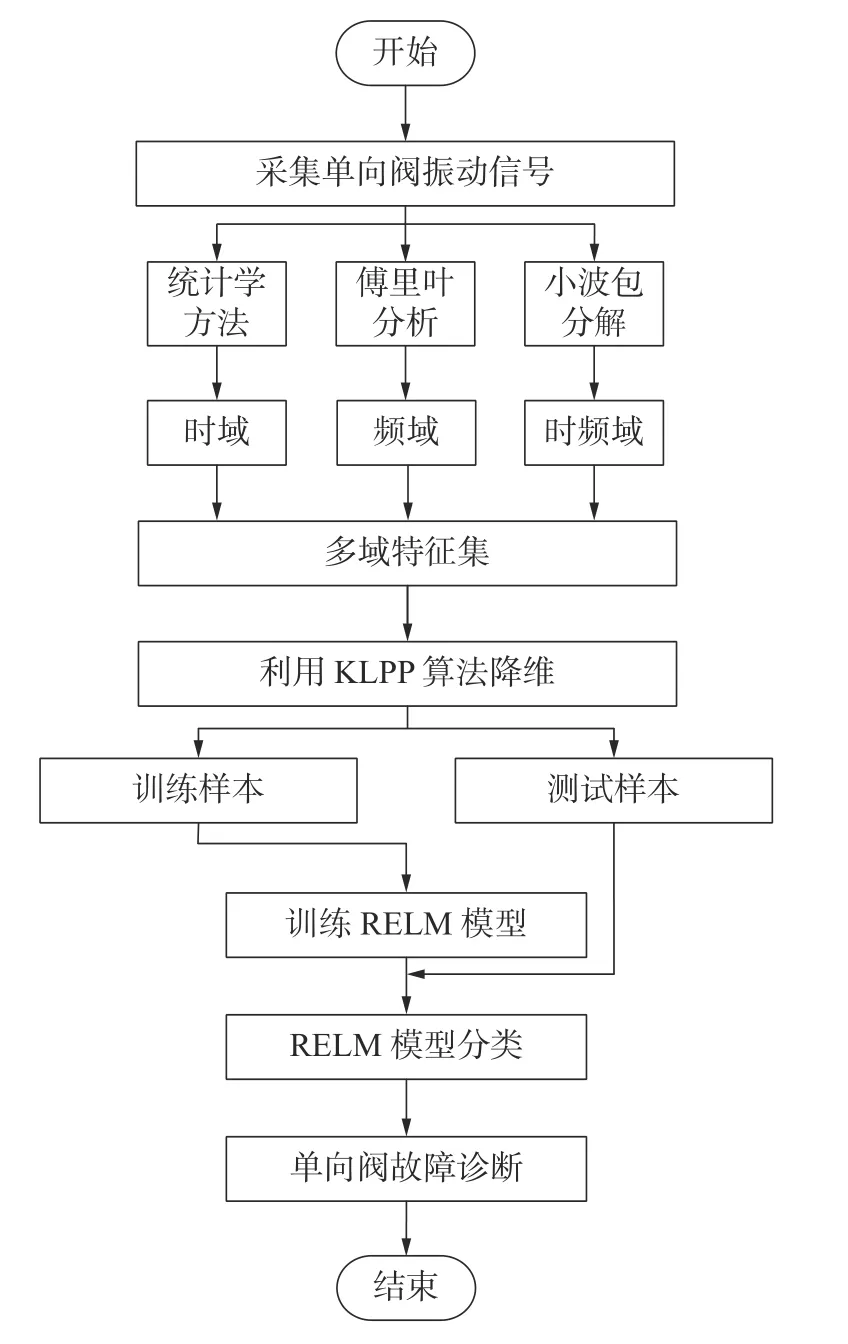
图1 单向阀故障识别流程Fig.1 The fault identification process for the one-way valve

步骤1数据采集：利用安装在高压隔膜泵单向阀上的加速度传感器采集其不同状态下的振动信号。

步骤2多域特征集构建：通过统计学方法、傅里叶分析和小波包分解3种方法分别提取时域、频域和时频域特征构建单向阀多域特征集。

步骤3维数约简：对单向阀多域特征集进行归一化，并采用KLPP 流行学习算法进行维数约简，消除该特征集的冗余信息。

步骤4故障诊断：将降维后获得的数据集中每种状态样本划分为训练样本和测试样本。训练样本用于构建RELM 故障诊断模型，测试样本输入训练完成的RELM 模型中进行高压隔膜泵单向阀故障诊断。

5 实验与分析

5.1 实验系统

实验数据为云南某铁精矿管型号为TZPM 高压隔膜泵站单向阀振动信号数据，属于三缸曲轴驱动的活塞式隔膜泵[20]。高压隔膜泵正常工作时通过电机驱动三拐曲轴、十字头、连杆进行往复运动，单向阀在进料和出料时会在作用力下正向或反向移动，实现物料的输送。高压隔膜泵工作原理图如图2所示。

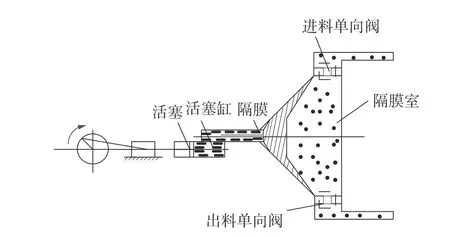
图2 高压隔膜泵工作原理图Fig.2 Working principle diagram of the high-pressure diaphragm pump

单向阀是控制物料从高压隔膜泵中进、出流动的关键部件，确保物料流入隔膜泵方向一致且不会逆流。隔膜泵单次冲程表示单向阀经历了一次物料进出的过程。假定隔膜泵的冲程时间为40 r/min,则单向阀一天需工作57 600次。单向阀在高压隔膜泵中需要保持频繁的周期性运行，因此最容易发生故障。

5.2 故障诊断实验分析

三缸曲轴驱动高压隔膜泵的3组进、出口单向阀成对工作，通过PCB-ICP 加速度传感器和型号为46 AE 的GRAS 传声器现场采集高压隔膜泵进、出口单向阀在正常、击穿和卡阀工况下的振动信号。本文选取其中一组单向阀的振动信号进行分析，振动信号的采样时间为30 s，采样频率fs=2 560 Hz，采样数据长度N=76 800。

本文按照时间顺序以1 280个采样点作为一个样本对单向阀振动信号进行划分，从而得到单向阀每种状态的60组样本数据。不同状态下单向阀振动信号的时域图如图3所示。

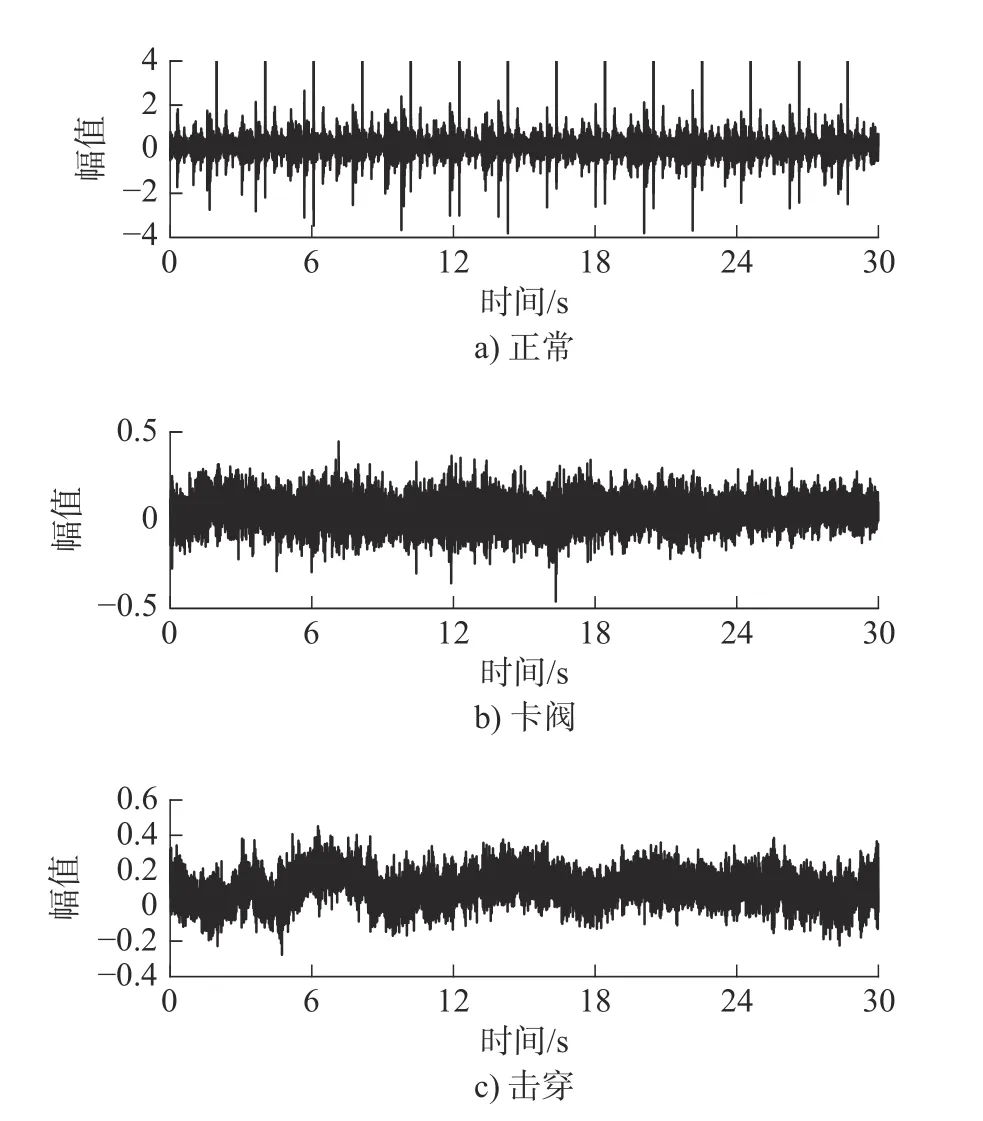
图3 3种状态时域振动信号Fig.3 Time-domain vibration signals in three states

单向阀振动信号单域特征所表征的故障信息较为有限。为了全面表征单向阀在不同工况下的故障信息，利用统计学方法和傅里叶分析对单向阀3种状态下的各60组样本分别提取16个时域特征和13个频域特征，频域特征如表2所示。并通过db5小波基对样本进行3层小波包分解，提取每个子信号的能量和能量熵特征获得16个时频域特征，从而可得180×45维的单向阀多域特征集。单向阀多域特征集中每种状态随机选取的两个特征样本如表3所示。在表3中，样本特征值依次为时域特征值T1～T16、频域特征值F1～F13和16个时频域特征值。

表3 单向阀3种状态多域特征样本Tab.3 Multi-domain features of the one-way valve in three states

为量化多域特征提取效果，本文将时域特征、频域特征、时频域特征以及多域特征经过归一化后输入构建的RELM 模型进行故障识别。RELM 隐含层神经元个数为10，激活函数为softplus。每类工况训练样本与测试样本按照5∶5随机分配，4种特征提取方法输入RELM 模型故障诊断结果如表4所示。单向阀多域特征的平均识别率高于任一单域特征。卡阀故障在3种工况的识别率最低的主要原因是卡阀状态本身就存在一些磨损，输送物料中的粗颗粒使单向阀处于卡阀状态，但在较短时间内粗颗粒顺利流过单向阀，又会使卡阀状态的振动信号与正常状态类似。

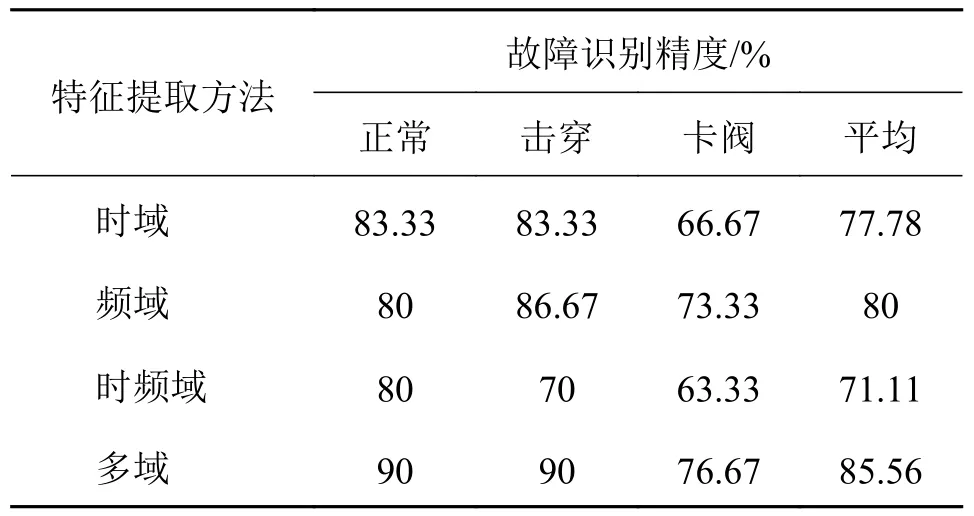
表4 单域和多域特征RELM 故障诊断结果Tab.4 RELM fault diagnosis results using single-domain and multi-domain features

多域特征集存在信息冗余，导致RELM 故障诊断模型识别精度较低，本文通过KLPP 算法对多域特征集进行降维，提取内部蕴含信息。为体现KLPP算法的优越性，将其与核主成分分析（KPCA）和局部保持投影（LPP）降维方法进行对比。3种降维方法前两维可视化结果如图4所示。KPCA 可将单向阀3种状态的样本基本分离，但是正常状态与击穿状态存在样本混叠现象，且各类样本较为分散，降维效果较差；LPP 能够将3种状态样本区分开来，样本之间边界较为明显，无明显混叠，但卡阀状态与击穿状态样本距离较近，正常状态样本分布不集中，降维效果较为一般；KLPP 可将单向阀3类样本完全区别开来，每类样本分布都比较集中并且样本之间具有明显的边界，在3种降维算法中效果最好。其原因在于：KPCA 为无监督降维方法，降维过程未考虑样本标签信息，对于单向阀这类存在大量奇异数据点的振动信号不太适合；KLPP 通过引入核函数挖掘数据中蕴含的非线性信息，从而达到比LPP 更好的降维效果。本文将类间距与类内距的比值作为性能指标对3种降维算法效果进行评价，当两者比值越大说明同类样本之间间隔越小，不同样本之间边界越明显，降维效果越好。KPCA、LPP和KLPP 算法的类间距与类内距的比值分别为2.3、3.85和61.34。上述算法降维可视化结果和降维性能指标值均表明了KLPP 算法对单向阀多域特征降维的有效性。

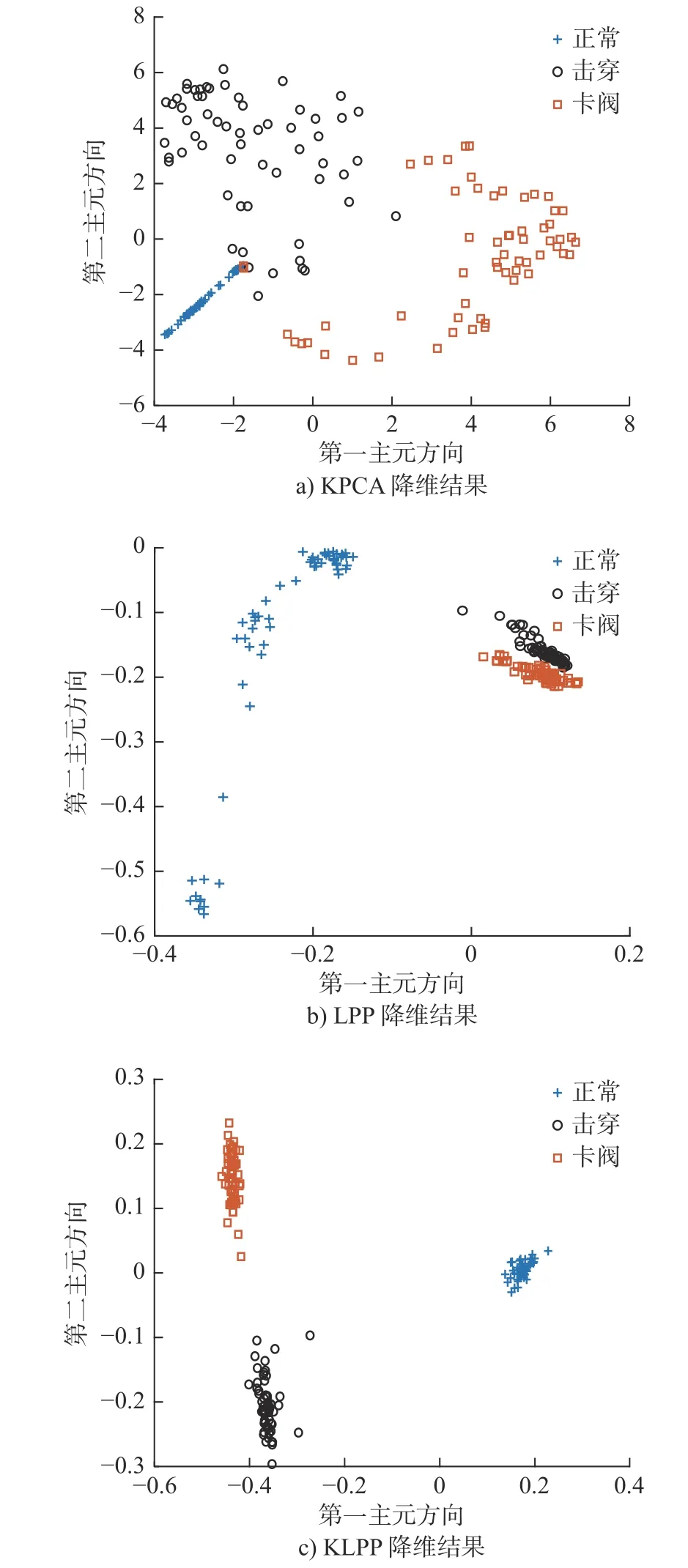
图4 3种算法降维可视化结果Fig.4 The dimensionality reduction visualization results of three algorithms

为了验证RELM 模型对单向阀故障诊断的性能，将ELM 模型与RELM 模型做对比。3种降维算法降维结果分别输入至ELM 模型和RELM 模型进行识别，结果如表5所示。KLPP-RELM 方法的正常状态和击穿状态的故障识别率达到100%，卡阀状态的识别率为96.67%，3种状态平均故障识别率为98.89%，与其他5种方法相比识别精度更高，表明了本文所提方法在单向阀故障诊断方面的有效性。KLPP-RELM 模型单向阀故障识别结果如图5所示。

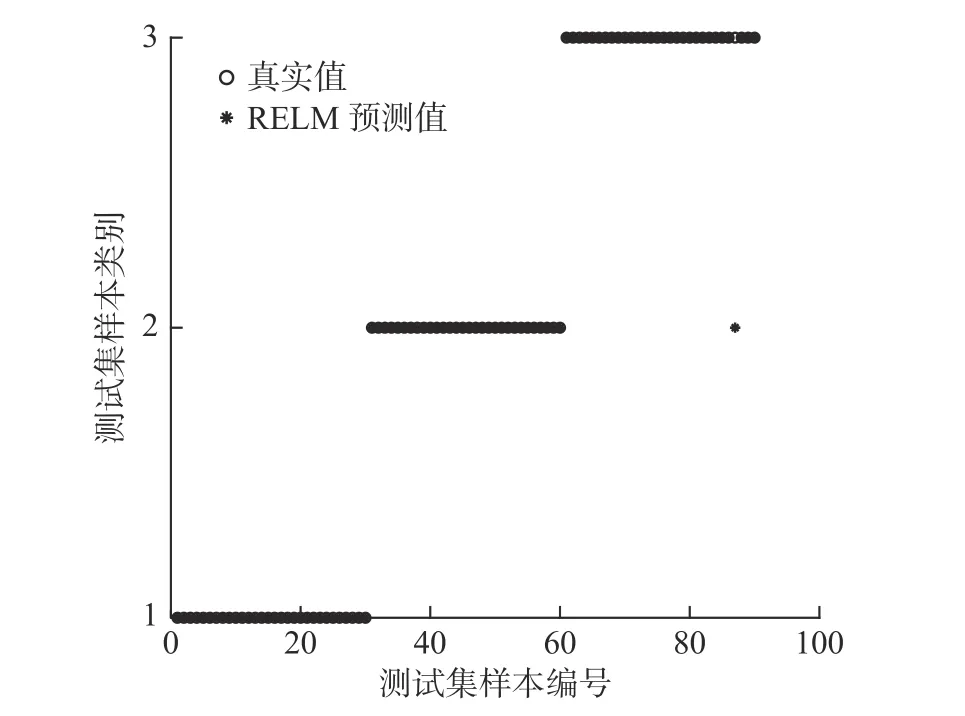
图5 RELM 模型故障识别结果Fig.5 Fault identification results for the RELM model

表5 多域特征降维后故障诊断结果Tab.5 Fault diagnosis results after dimensionality reduction of multi-domain features

6 结论

本文采用多域特征表征单向阀运行状态，基于多域特征维数约简，构建了基于KLPP 和RELM 的高压隔膜泵单向阀故障诊断模型。克服了多域特征的信息冗余问题，并通过引入正则项，提升单向阀故障诊断模型的泛化性能。结论如下：

1）多域特征可以完整表征单向阀运行状态，克服了单域特征无法全面表征单向阀的运行状态的问题。

2）采用了KLPP 算法对多域特征集进行降维，避免了多域特征集维数灾难的问题，克服了高维特征信息冗余的问题。

3）基于KLPP 和RELM 的故障诊断模型，采用正则化方法控制ELM 模型的拟合程度，提升了ELM 模型的泛化能力。与ELM 模型相比，RELM故障诊断模型识别准确率达到98.88%，可以准确识别出单向阀的故障类型。