基于最小二乘法的预制节段梁拼装线形控制*

陈新元,刘广辉,唐 超,赵 波

(中建三局基础设施建设投资有限公司,湖北 武汉 430061)

0 引言

预制拼装技术将梁体纵向划分成若干节段,梁段在预制梁场进行统一生产,在现场拼装架设。目前,工程上多采用短线匹配法控制预制节段梁的空间位置,以进行节段梁的预制。预制节段梁悬臂拼装技术误差累积效应明显,前一节段梁的偏移会影响后续节段的拼装,甚至影响整个桥梁结构的线形。因此,如何分配及消除预制与拼装中的误差显得十分必要。为使分段拼装后的梁体能满足设计线形的要求,需从预制阶段开始识别并调整桥梁施工偏差进行施工线形控制,直到梁段拼装完成。预制过程中通常以梁顶面中心线为基准线来描述其线形,并利用局域坐标转换法进行误差获取与线形控制。不少学者对相关原理进行了研究[1-5];罗桂锋[6]针对节段梁的拼装影响因素及误差进行了研究,通过数值分析,总结了节段梁拼装控制要点;潘志群[7]阐述了“双U+箱形”变截面梁节段拼装过程,利用多种技术手段进行线形控制,效果较好。

目前,针对线形控制中拼装阶段误差改正数的确定与选取研究较少。改正数(即误差调整值)的大多数直接取误差的相反数,误差较大时,这种一次性消除误差的改正数取值会造成该节段出现较大折角,影响外观,对于曲线形节段梁还需特殊考虑,十分不便。因此,本文针对拼装阶段提出基于最小二乘法的拟合线形控制方法,将较大的误差分配到后续多个节段中,并逐段进行改正调整,以平缓节段折角,实现线形控制。

1 预制节段梁现场施工线形测量控制

1.1 节段梁施工测量控制要点

本工程节段梁为“双U+双箱”叠加组合结构,桥梁底面设计为二次抛物线形,同时梁宽度逐段加宽,采用短线法在梁场预制,采用悬拼吊机现场拼装。变截面U箱组合节段梁在现场施工的线形控制要点主要为墩顶块施工、首节节段梁及后续节段梁拼装的测量控制[8-9]。现对各环节测量工作及线形控制进行说明,具体流程如图1所示。

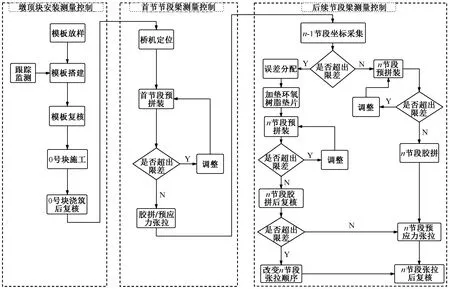
图1 悬拼线形控制流程Fig.1 Suspended linear control process

1.2 墩顶块施工的测量控制

根据建设单位提供的测量导线控制网和高程控制点,建立适合本工程的测量定位轴线网络和标高控制网络。其中,重要的控制坐标要做成相对永久的坐标点,并妥善保管至竣工验收。

施工前应先校核墩顶块平面控制点及高程控制点,复核支座顶面高程,并在施工过程中确保支座位置不发生偏移。墩顶块底模铺设完成后,及时复核底模高程,检查底板横断面尺寸是否正确,确认无误后方可进行下一道工序。

为保证后续施工精度和拼装顺利进行,模板定位要准确,并在模板搭建过程中进行监测复核,让测量控制贯穿全过程。模板的定位放样及复核精度在实测中应适当高于规范要求。墩顶块经反复测量定位与调整,各轴线精度严格控制在3mm以内。墩顶块施工验收标准如表1所示。

表1 墩顶块施工验收标准Table 1 Construction acceptance standard of pier top block

1.3 首节节段梁拼装的测量控制

预制节段梁首节段的拼装是成桥线形控制的重中之重,其安装精度将直接影响后续梁段的整体线形,决定后续节段的走向和高度,因此在实际施工过程中应适当提高首节段拼装精度控制标准,同时借助全站仪精确控制轴线,用水准仪参照二等水准标准测得高程,通过施工过程中的偏差反馈和调整,使其严格控制在限定误差范围内。首节段拼装如图2所示。

图2 首节段拼装Fig.2 First segment assembling

墩顶块浇筑完成后首先应进行悬拼吊机的定位,由于悬拼吊机在横桥向移动距离有限,为保证首节节段梁及后续节段梁在吊装过程中有足够的调整空间,应尽可能地确保悬拼吊机中轴线与节段梁中轴线处于同一纵断面。

根据左右边腹板上4个控制点确定首节节段梁高程后,通过全站仪采集中腹板上2个控制点坐标,求出轴线偏移方向及偏移量,利用悬拼吊机横向液压装置进行横向移动,调整轴线。

调整完成后继续按先左右高程、再中心轴线的顺序反复进行复核调整,确保首节节段梁的高程及轴线偏位在标准允许范围内,同时与墩顶块能较好地拼接。首节节段梁采用六点法线形控制,轴线允许误差为同向1mm以内,高程允许误差为同向2mm以内。合格后焊接劲性骨架进行临时锁定,在一天中温度最低且相对稳定的时间段浇筑湿接缝混凝土,待强度达到要求后,进行永久预应力张拉。首节节段梁拼装验收标准如表2所示。

表2 首节节段梁拼装验收标准Table 2 Acceptance standard of first segment beam assembly

1.4 后续节段梁拼装的测量控制

首节节段梁准确就位施工完成后,进行后续节段梁的拼装工程。

以第n块节段梁为例,首先采集上一节段梁(n-1)的高程及轴线偏位数据,并与设计值进行核验,对比限差标准,判断是否需在本节段梁进行线形调整控制。采用的限差标准为验收标准的1/2,均为5mm。若第n节段允许偏差在限差标准以内,则采用常规线形控制标准,正常进行后续节段梁的拼装施工;若第n节段允许偏差超出限差标准,则需进行误差分配调整分析,再根据分配结果(改正数)进行线形调整。

该阶段线形控制主要采用导向性拼装工艺,即在节段梁间加垫环氧垫片(5～8mm),以调整节段梁的高程和轴线偏差,然后进行预拼装,拼装后复测校核,根据复测结果调整临时预应力张拉顺序作为辅助手段,导向性地进行节段梁拼装,以达到控制线形的目的。后续节段拼装如图3所示。后续节段梁拼装验收标准如表3所示。

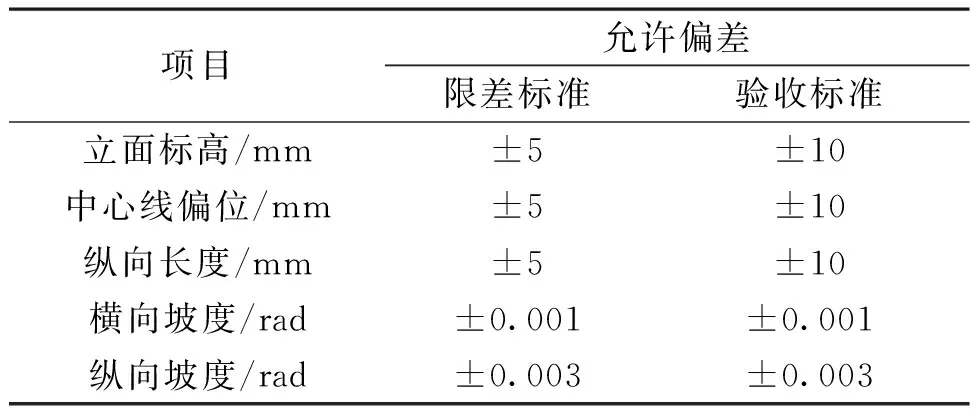
表3 后续节段梁拼装验收标准Table 3 Acceptance standard of subsequent segmental beam assembly

图3 后续节段拼装Fig.3 Subsequent segment assembling

2 拼装阶段拟合线形计算方法

预制节段梁现场施工过程中节段拼装占较大部分,除墩顶块外,其余节段均为悬臂拼装。由于误差的累积作用,通常超出限差的情况会出现在3号节段以后。因此后续节段往往要进行线形控制。

本文基于最小二乘法对六点法采集的各离散坐标数据进行拟合,并以此来确定改正数,处理误差。

2.1 六点法测量

利用梁面的6个控制点即可对节段梁悬臂拼装进行定位。6点坐标即为测量控制点坐标,在短线法节段梁预制过程中,根据线路的设计参数(桥梁的平、竖曲线及理论预拱度)确定整体坐标系,在待浇节段两侧边腹板预埋高程控制点,中腹板顶面预埋轴线控制点。

2.2 误差计算

高程的误差用实际采集的数据值减去理论数据值求得:

Δh=h′-h

(1)

式中:h为轴线设计值;h′为实际测量值;Δh为高程偏差。

轴线偏差的确定如图4所示。A,B为6点法中腹板轴线设计值,A′,B′为实际测量值,之间存在的偏差Δ为实际偏差。沿大里程方向左侧偏差值为正。

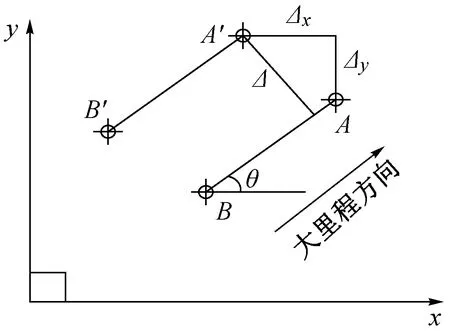
图4 轴线偏差示意Fig.4 Axis deviation diagram

(2)

Δx=XA-XA′

(3)

Δy=YA-YA′

(4)

Δ=-Δycosθ+Δxsinθ

(5)

式中:θ为轴线夹角;XA为A点横坐标;YA为A点纵坐标;XA′为A′点横坐标;YA′为A′点横坐标;Δ为实际偏差;Δx为横坐标差值;Δy为纵坐标差值。

2.3 最小二乘法线形拟合

由于市政工程高架桥的预制悬拼对桥梁外观有较高的要求,在保证符合规范、不影响桥梁结构的基础上对工程提出了更高的要求。假定在预拼装第m节节段梁出现几何误差超过规定限值,由于m-1梁段已安装成型,预应力张拉完毕,形状不能改变。因此第m节梁段拼装后的几何误差只能在本段梁胶拼前和后续梁段拼装过程中进行修正。若只在本阶段进行调整,会出现较大折角,影响桥型美观甚至影响结构安全性,因此须对误差进行分配,保证节段梁拼装线形的连贯性。为此,需计算余下各点的改正数。最小二乘法是处理不连续离散点的一种数学工具,适合处理6点法控制测量采集的数据,具有较好的适应性。

对梁段进行拟合时,应选择拟合所用的坐标参数。未拼装时设计数据是唯一参数,拟合出的线形与设计线形一致;拼装开始后,已拼装好的节段相较于设计值会出现误差,并对桥向拟合产生影响。因此,对已安装完成的节段采用实测坐标数据代替设计数据,未安装的节段仍用设计数据,将2组数据作为参数共同参与拟合,得出近似拟合线形,并随施工的推进不断对坐标参数进行迭代更新,直至完成。

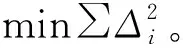
Δi=-Δycosθ+Δxsinθ

(6)

2.3.1直线段预制节段梁的线形拟合

直线段预制节段梁的线形拟合采用直线拟合线性函数法。直线段预制节段梁如图5所示。

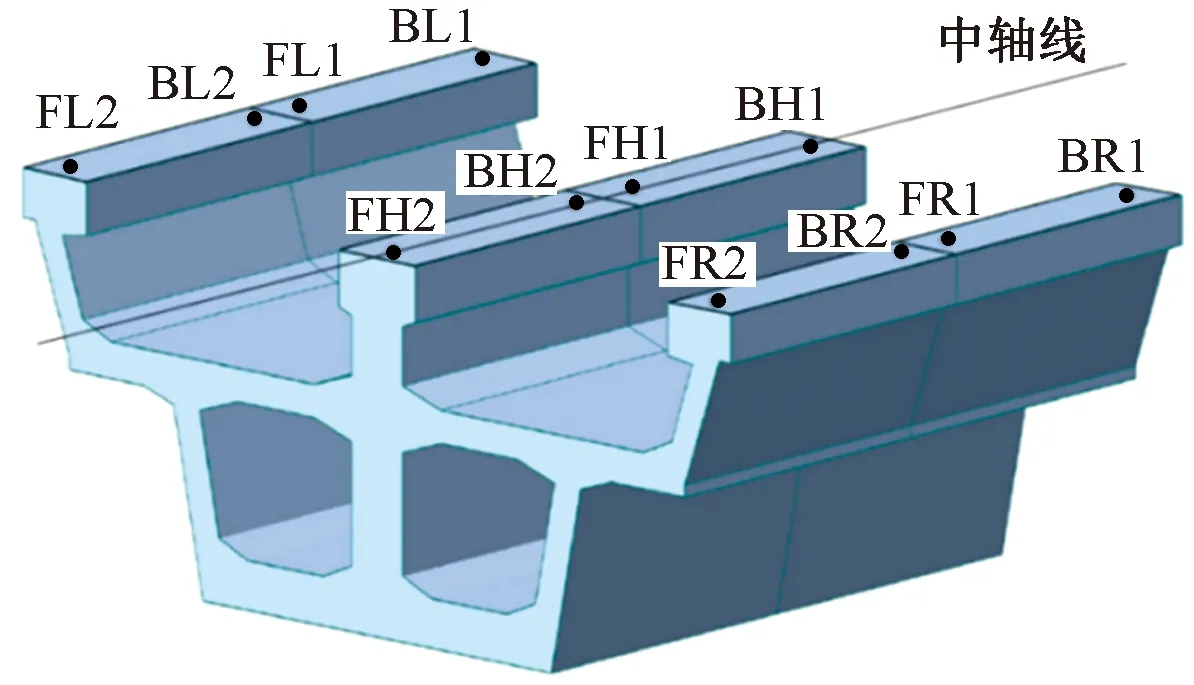
图5 直线段预制节段梁Fig.5 Prefabricated segmental beam in straight section

假设线性关系为:

(x)=ax+b

(7)

误差函数为:

Δ=∑((x)-yi)2=∑(axi+b-yi)2

(8)

在误差公式中,不同a,b会导致不同的Δ,根据多元微分,当他们的偏微分为0时,Δ取最小值,得出a,b的值。

2.3.2曲线段预制节段梁的线形拟合

曲线梁桥线形较复杂,施工过程中大部分采用曲线直做法降低施工难度,该做法造成轴线线形控制时带有一定的系统误差,增加了拼装控制的难度,也会造成误差改正计算不准的现象。因此,为保证桥梁线形的准确性,制作过程中控制点的预埋及拼装改正数的计算均应以曲线线形为依据。本文对曲线段预制节段梁的线形拟合,采用多项式拟合非线性函数方法。曲线段预制节段梁如图6所示。

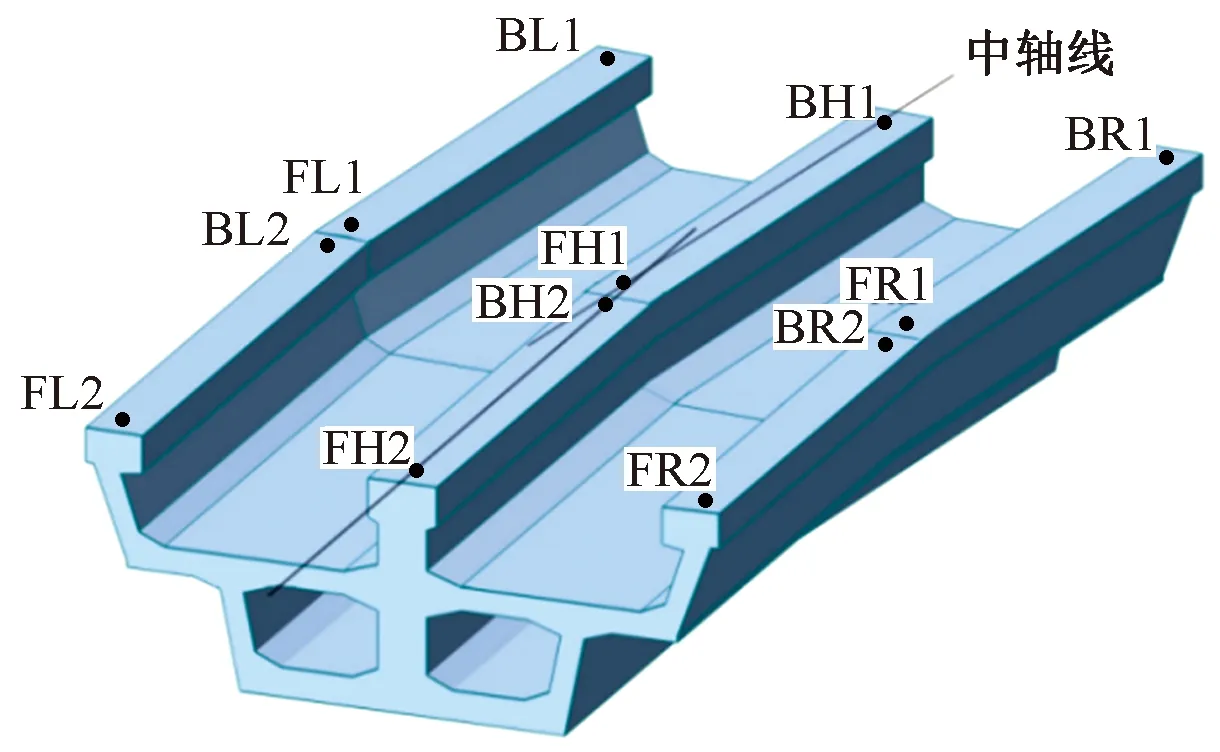
图6 曲线段预制节段梁Fig.6 Curved precast segmental beam

通常使用高次多项式近似表示函数:

f(x)≈pn(x)=a0+a1(x-x0)+

a2(x-x0)2+…+an(x-x0)n

(9)

式中:pn(x)的各阶导数和f(x)的各阶导数均相等,则f(x)和pn(x)的误差为 (x-x0)n的高阶无穷小。

用f(x)的真实函数值减去多项式函数结果的平方来表示f(x)和多项式函数的误差关系:

a2(x-x0)2+…+an(x-x0)n]}2

(10)

令其在0点处展开,得到:

f(x)=a0+a1x+a2x2+…+anxn

(11)

(12)

对每个系数求其偏导,并令其为0,求解方程组,得出各系数的值。

同理,对于高程的误差控制,定义ν为设计值与实测值之差:

(13)

最小二乘法的目的是使∑νi最小,计算过程与轴线相同。

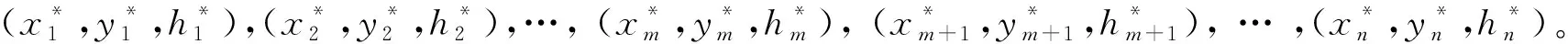
Vx=x*-x

(14)

Vy=y*-y

(15)

(16)

综上所述,采用最小二乘法对误差进行修正,将出现的误差合理分配到后续拼装的各梁段中,确保成桥线形达到最佳的拟合线形。通过上述方法,利用已安装梁段(n节段前)采集的最终坐标数据与未安装节段(n节段以后)的设计数据,通过最小二乘法对线形进行回归估计,得到在设计线形误差允许范围内的拟合线形,计算出n节节段梁及后续节段梁的坐标,并依据拟合线形求得后续节段梁的改正数V。

3 桥梁线形控制应用与实践

3.1 数据采集

本文主要应用六点法进行数据采集,由于施工空间有限,通视效果较差,特别是在中跨末尾几个节段,视线阻挡十分严重,给轴线观测带来较大的难度,若采用传统的直线定位法难度较大。六点法的优势是采集数据较少,各点间无需通视,只需采集点位数据就能通过计算得到线形。

施工前根据阶段梁拼装的具体位置布设控制点,应考虑测量采集数据的便利性,利用六点法数据采集时,为保证数据的精度,应将全站仪架设在控制网中的一个具体控制点上,利用其余控制点做后视定向。通视不能满足时可考虑用悬垂法获取高程或增加控制点。

3.2 线形控制

在预匹配阶段对采集的各点数据与理论数据做差,得到误差值,根据六点法原理,得到边腹板的高程误差数据和中腹板的轴线偏差数据,以允许偏差控制标准为依据判断是否进行线形调整,当误差值超过控制标准则采用最小二乘法进行线形拟合,确定改正数,根据改正数进行调整。主要通过增加环氧垫片和改变预应力张拉顺序进行调整,节段张拉完成后再对数据进行采集,作为该节段的最终坐标数据,并以此判断该节段是否已调整到合适位置,在下一个预匹配阶段应做出的相应调整。

3.3 工程实例

以本工程中一联节段梁安装轴线拟合为例,设计数据如表4所示。

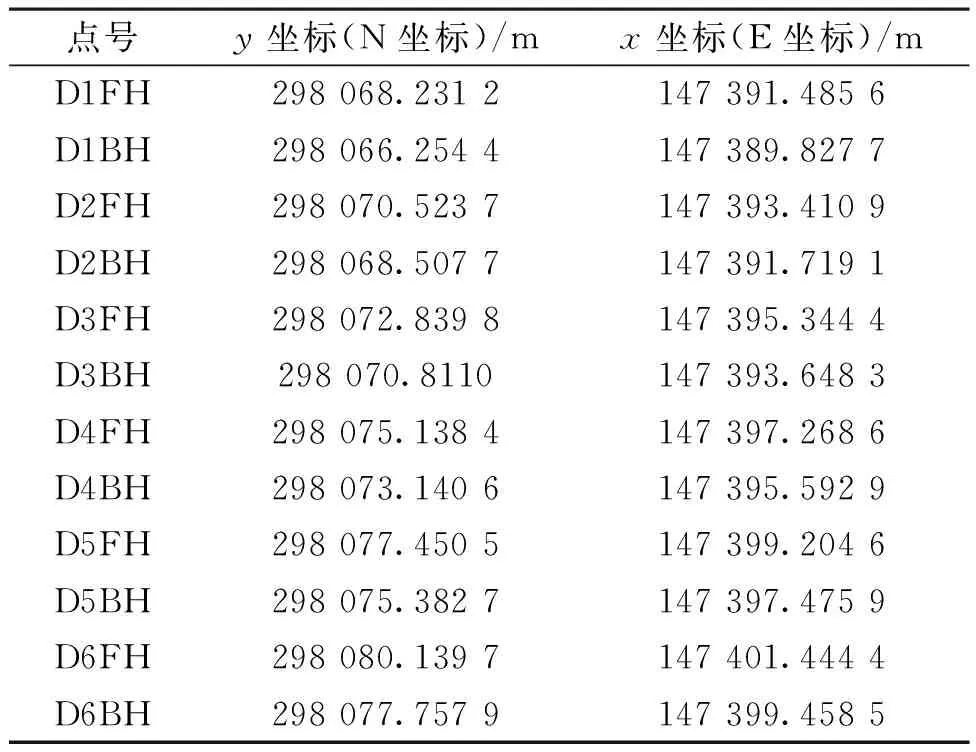
表4 节段梁拼装设计数据Table 4 Segmental beam assembly design data

利用设计数据拟合出设计线形,如图7所示。

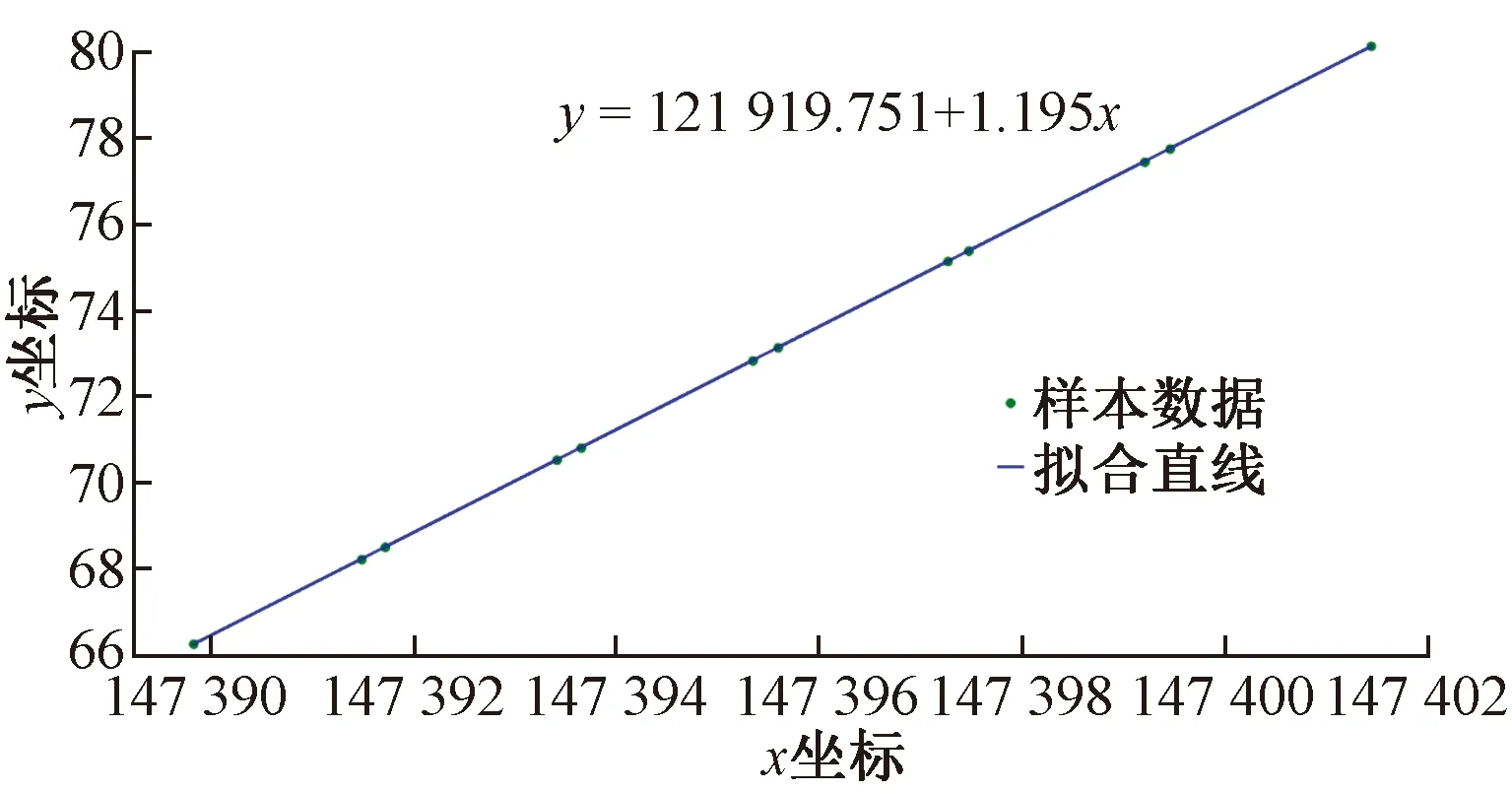
图7 直线预制节段梁设计拟合直线Fig.7 Design fitting straight line of straight line precast segmental beam

由图7可知,设计线性各点位成一条直线,数据点全部在拟合直线上。本文中的拟合图像全部利用Python 提供的scipy库自主编程计算得出。

每拼装好一个节段后对点位进行采集,结果如表5所示。当节段梁拼装到第4节段时出现拼装后采集的数据偏差过大,故采用本文提出的最小二乘法拟合来重新计算线形。

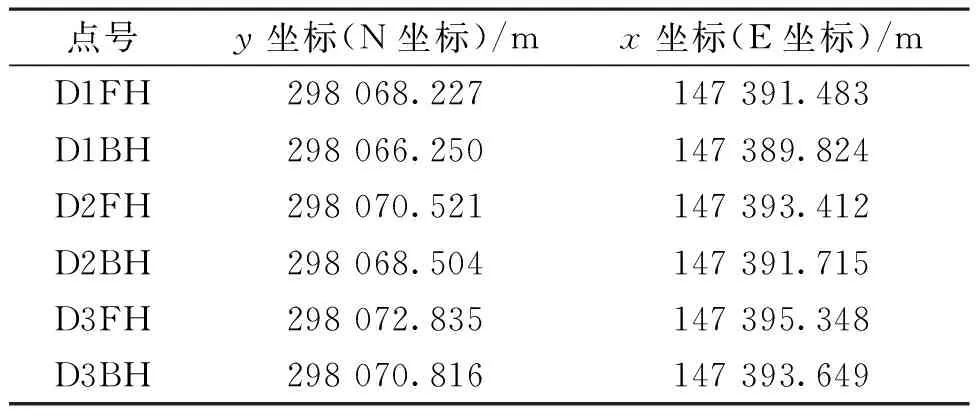
表5 节段梁拼装拼装后采集数据Table 5 Data collection after segmental beam assembly

D1FH～D3BH采用采集数据,即已安装好的实测数据,D4FH～D6BH继续采用设计数据,拟合出近似拟合线形,如图8所示。

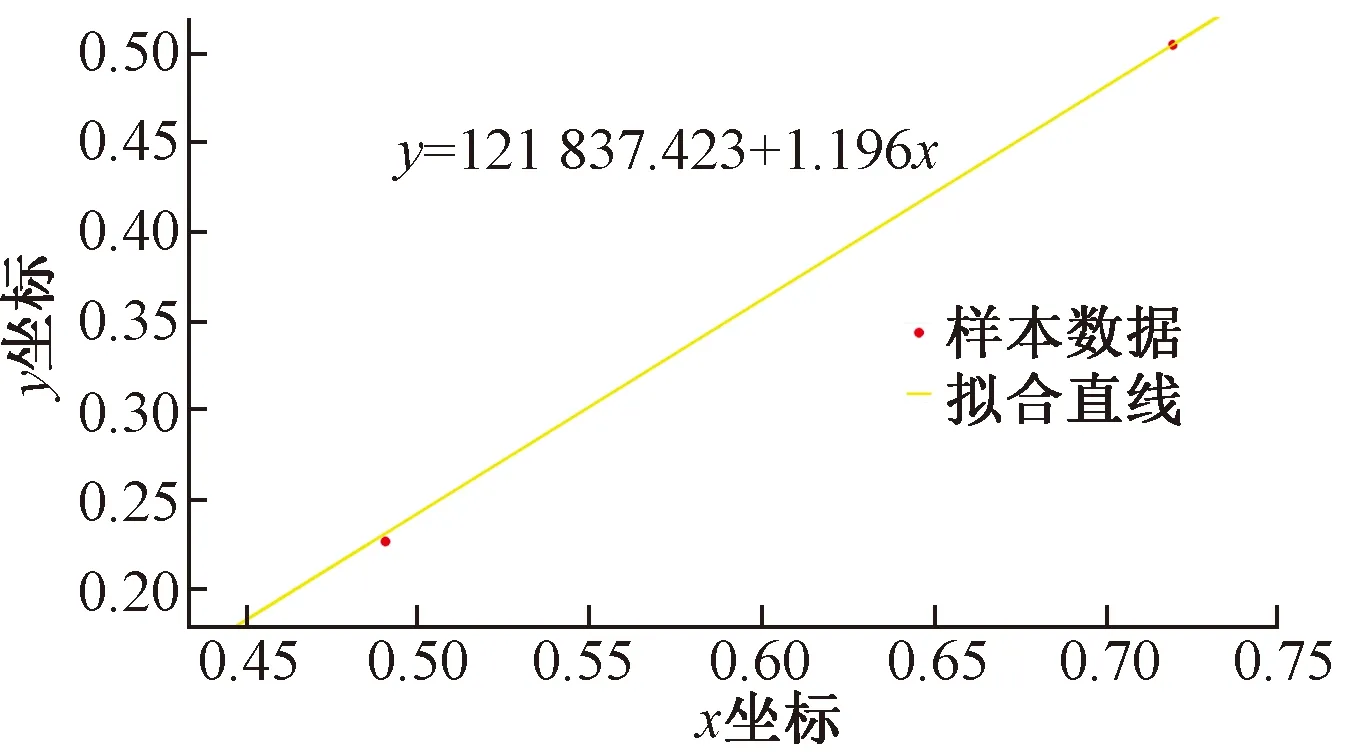
图8 直线预制节段梁数据近似拟合直线(局部放大)Fig.8 Linear prefabricated segmental beam data approximate fitting straight line (local amplification)

由图8可知,数据点并未全部在拟合直线上。在误差纠正时后续点位应与近似拟合直线重合,而不是直接与设计拟合直线重合。

3.4 结果分析

节段梁悬臂拼装时的线形控制点与其预制时所用的控制点相同,通过对比实测节段梁数据与设计值,得到误差折线,如图9所示。

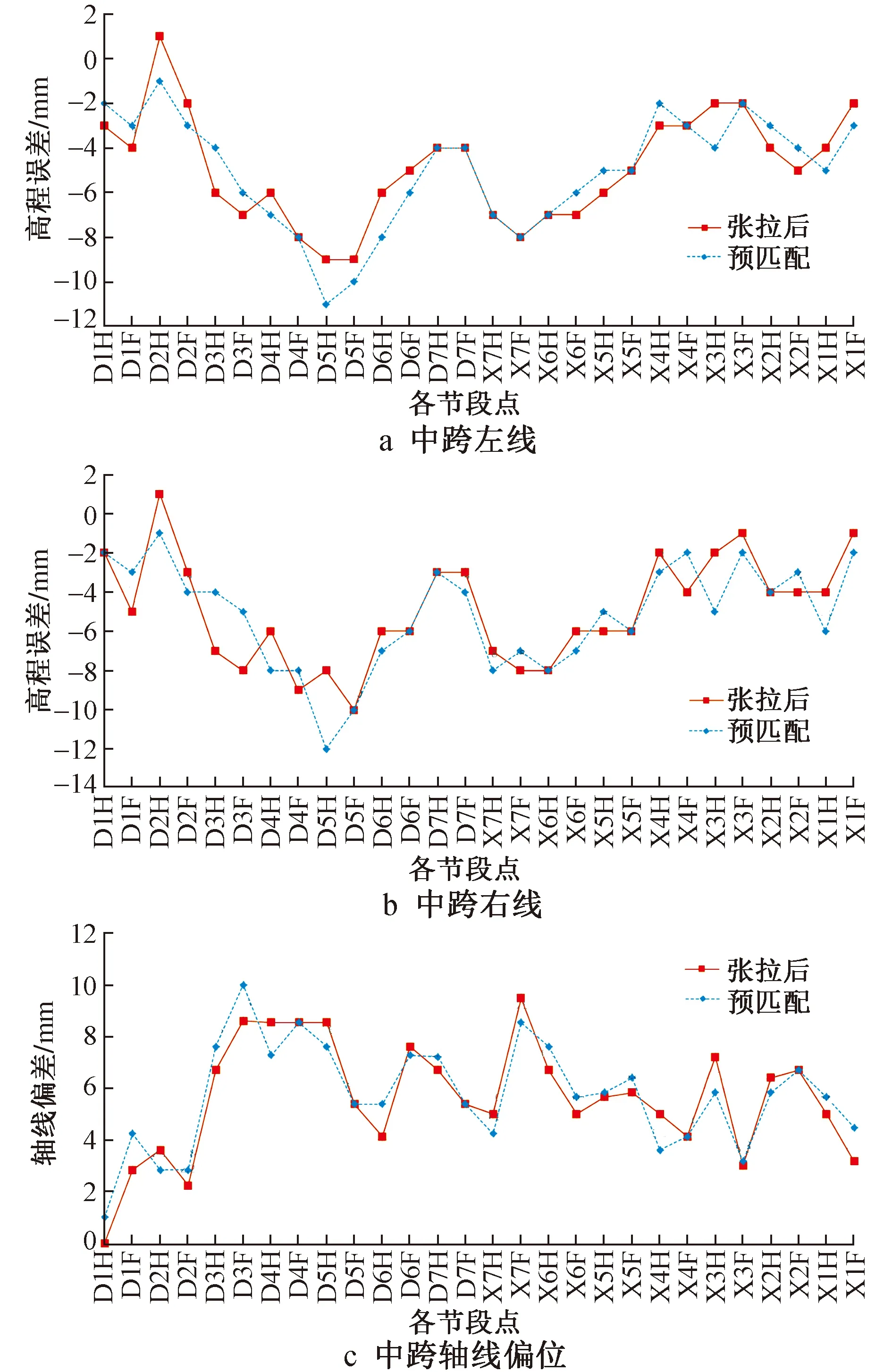
图9 误差折线Fig.9 Error broken line

由图9a,9b可知,左、右线节段梁标高均出现超过限差标准的情况,且均出现在D4F,D5H处,通过最小二乘法线形拟合调整后,可看到无论是预匹配还是张拉后折线误差均逐步回归;较平缓地将节段梁的误差回调至限差标准范围内,最终在D7F,X7H处中跨合龙时误差符合标准,实现线形的平稳过渡。

由图9c可知,当误差较大,出现超过限差标准的情况时,通过线形拟合调整,可使节段梁的误差逐渐回归至限差标准范围内,整体线形趋势逐渐向拟合线形靠拢。最终在D7F,X7H处中跨合龙时虽相较于设计轴线整体向左略有偏移,但误差在合理范围内,符合设计要求。避免出现过大折角的情况,顺利完成合龙。

4 结语

本文讨论了预制节段梁现场施工全过程的线形测量控制,将最小二乘法应用于预制节段梁的拼装过程中,提出一种拼装阶段拟合线形的计算方法,论述了直线形和曲线形的预制节段梁拟合计算过程,并以工程实例对成桥后实测线形与理论线形的误差进行对比分析,说明本文提出的线形拟合计算方法基本可行,并具有一定的实用性。该方法能准确给出改正数,并通过调整使误差缓慢回归,避免出现大的折角,取得较好的线形控制效果。