雷达目标识别评估中的数据可分性度量方法

姜卫东 薛玲艳 张新禹

(国防科技大学电子科学学院 长沙 410073)

1 引言

测试和评估是目标识别模型中重要的组成部分，是衡量模型性能的重要手段[1]，识别评估方法相对识别模型的研究滞后[2]，这在一定程度上限制了目标识别模型实用化发展。目前在评估阶段，研究学者更倾向于在特定数据集上给出识别准确性指标来评价所提模型的性能优势[3]。该方法仅从识别率一个方面评价了模型性能，无法反映在输入数据发生变化时识别模型的泛化能力[4,5]。其原因是面向模型的准确性评估指标无差别地对待了每一个数据集，忽略了数据集可分性对识别性能造成的影响[6]。识别性能与数据可分性密切相关，识别性能的评估应当结合对数据特性的评估，以满足对模型泛化性能的评估需求。考虑到真实雷达目标识别场景的多样复杂与动态变化特性，要求实用化的目标识别模型应当具备一定的泛化能力。因此针对某个特定的识别任务，如基于雷达散射截面积 (Radar Cross Section,RCS)、基于高分辨距离像 (High-Resolution Range Profile,HRRP)或基于逆合成孔径雷达 (Inverse Synthetic Aperture Radar,ISAR)像的目标识别任务，需要在不同观测条件的数据上测试模型以评估其应对复杂目标识别环境的泛化性能。而评估模型泛化性能离不开对识别场景的描述，因此提出数据可分性度量量化模型所处识别条件。

数据可分性是在给定标签条件下，描述数据中属于不同类别的样本间混合程度的一种固有属性[7]。在已知数据标签条件下，可以以具体的识别任务为导向，确定样本依其类别在特征空间的分布，数据整体分布的扩展率与类别子空间类内分布的压缩率共同构成数据可分性的衡量指标。可分性较好的数据具有较大的整体分布散度与较小的类内分布散度，表明类间样本相关性弱而类内样本相关性强。精确描述数据可分性有利于探究模型识别性能边界，能够预先为识别结果提供参考基准，为模型性能评估与改进提供支撑。

数据可分性度量为建立具有一定难度梯度的标准测试数据库提供依据，为实现层次化、轻量级的模型泛化性能评估过程打下基础。雷达目标识别数据集的可分特性受到目标所处环境、传感器状态等因素的影响，待识别的任务是在不同信噪比、不同信杂比、不同分辨率、不同观测角或不同频段下的目标散射特性信息集合。若将模型同时测试在上述所有状态的数据集上，不仅耗费时间成本，并且无法得出指导性的评估结论，因此考虑一种更为轻量高效的层级式模型性能测试方法。如图1，层级式模型识别性能评估中，模型由易到难每次测试在一个难度级别的数据集上，通过设置一定的识别率门限作为模型通过某层数据集测试的条件，模型在最终未通过测试的数据层所表现出的识别率代表了模型的性能上限，而模型通过测试的各数据层则体现模型性能的泛化范围。上述测试方法的实施建立在对大规模数据按照其识别的难易程度进行分层的整理和归纳的基础上，量化的数据可分性数值标定了数据的识别难度，为数据分层提供科学的依据。

图1 层级式模型识别性能评估示意图Fig.1 Hierarchical model recognition performance evaluation schematic

数据复杂度标定了识别任务难度[8]，决定了模型识别性能上限[9,10]。文献[11]将数据空间的结构与特性分析列为人工智能的重大数理基础问题之一。文献[12]研究表明可分性因素的分析有利于辅助预测识别模型的性能。文献[13]认为可分性度量可以应用于识别模型选择、特征挑选算法、聚类算法、生成对抗网络性能的评估，以评估挑选的特征、新聚类的数据及新生成样本的可分性。文献[14]依据分类复杂度设计了动态多分类器决策方法。文献[15]将可分性度量结合到自编码器网络损失函数的迭代过程中，实现了对数据更可分低维特征的提取，将提取的隐藏层特征应用在下游识别任务中，提升了识别性能，并在评估阶段将特征可分性作为网络性能评估的指标之一。因此将数据可分性度量结合进雷达目标识别评估过程，对解释、指导模型性能改进具有重要实际应用意义。

现有数据可分性度量方法大都基于对数据简单统计特性或对样本间距离的分析。文献[16]从数据可分性角度总结了现有分类复杂度的度量方法，该文献将数据复杂性度量归为6类。其中，基于统计特征的分析方法仅利用了数据的均值和方差特性；线性度量方法主要依赖于线性分类器的识别结果；近邻度量方法更侧重于分析数据的局部距离信息；网图度量方法主要衡量样本点依据一定准则所构成的图结构密度；样本数与维度数指标主要用于描述类不平衡性及降维复杂度。上述方法仅反映了数据的局部特性，其有效性大多基于数据的线性可分假设，无法区分具备非线性划分结构的特征族可分性差异[17]。文献[13]验证了基于统计特征、线性分类器、样本数与维度数的度量方法无法有效衡量数据可分性；而基于邻域和网图的距离度量方法则具有较大的计算量，并且在衡量类间重叠度的实验中不再适用。

为解决上述度量失效问题，本文考虑从概率论的角度解释数据可分性。根据贝叶斯准则，假设每个类别出现的概率相等，则样本分类的结果取决于每个类别相对应的似然函数大小[18]。此时各类别的似然函数差距越大，数据就越容易划分开。然而由于高维数据的复杂性，似然函数建模比较困难。文献[19]表明最小化数据编码率的过程等价于求解似然函数的最优解，即数据编码速率和参数估计性能具有强一致性[20]。这意味着如果按类别编码后的数据可以用更好的概率分布模型拟合，则该数据在给定失真率下具有较小的编码量。文献[21]认为，率失真函数为实值混合数据的分割优度提供了一种自然的衡量标准。在最近的研究中，率失真理论被用于解释神经网络模型[22]、优化特征学习方法[23,24]等。

本文的主要贡献在于基于率失真理论量化数据整体分布散度与类内分布散度，通过构造两种分布散度的比例关系提出了一个新的数据可分性度量，该度量综合了数据经奇异值分解后各个正交特征维度上的可分性信息，能够评估多维高斯分布数据的可分性优劣；结合高斯混合模型，该度量能够衡量非高斯分布数据的类间重叠度，度量效果相对现有方法具有明显优势。在仿真数据上对所提方法进行了测试，结果表明由所提方法计算的可分性度量值在二维数据上与特征散点图可分性的直观判定结果对应，并且能够衡量加噪数据的可分性优劣；在高维实测数据[25]上的识别难度评估实验表明所提度量与模型统计得到的平均识别率具有强相关性，其能够以独立于识别过程的方式量化数据识别难度，预先为识别结果提供评判基准；最后本文将所提度量应用在识别网络特征质量评估中，在测试阶段量化分析了网络提取特征的可分性变化趋势，在训练阶段将特征可分性作为损失函数的一部分来同时优化特征质量，从特征可分性的角度为网络识别性能的评估与提升提供新思路。

2 相关工作

本节总结本文所用到的对比方法，其特点是利用样本间的距离信息构造可分性度量。文献[26]总结了一系列近邻方法，如描述类内距与类间距相对比值的方法(Ratio of Intra/Extra Class Nearest Neighbor Distance,N2)以及一种统计局部近邻数量的方法[27](Local Set Average Cardinality,LSC)；基于网图的方法如网图平均密度法(Average Density of the Network,Density)[28]主要描述依据一定距离判决准则所构造的网图邻接边数量；此外文献[13]提出基于距离的可分性度量指标(Distance-based Separability Index,DSI)，其主要利用类内距与类间距分布之间的差异信息。下面介绍上述度量方法的计算原理及特性。

(1) N2

N2度量方法设数据X=[x1,x2,...,xm]∈Rn×m由具有n维特征的m个样本构成，计算样本xi到其最近邻同类样本 NN(xi)距离d(xi,NN(xi))及xi到其最近邻异类样本 NE(xi) 的距离d(xi,NE(xi))，取m个样本的d(xi,NN(xi)) 之 和与d(xi,NE(xi))之 和的比值即为度量N 2。由于N 2 的数值范围取N2∈[0,∞)，因此通过数值转换将其规范到0～1之间，且值越大，表明数据越不可分，如式(1)

式(1)表明度量N2利用的是样本与其近邻样本的距离信息，关注的是样本周围的可分性，每个样本的可分性都仅与距离其最近的样本相关，因此该度量只能反映数据的局部结构特性，对于距离各个类别较远的离群样本，度量N2将无法刻画其可分性。

(2) LSC

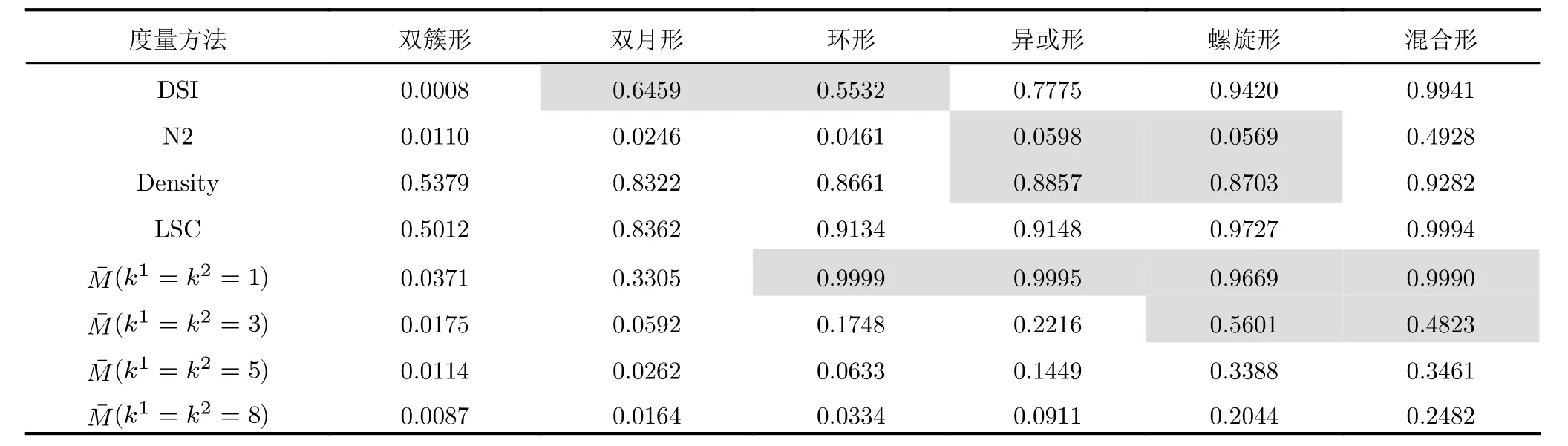
LSC度量方法设样本xi与xj的距离为d(xi,xj)(i≠j)，xi到其最近邻异类样本N E(xi)的距离 为d(xi,NE(xi))，则| LS(xi)|定义为满足条件d(xi,xj)

式(2)表明LSC赋予距离异类样本更近的样本更大的值，意味着其认为处于异类样本分布中或处于决策边界附近的样本点导致可分性的恶化，因此更适用于度量决策边界的复杂度。虽然LSC相对N2更多考虑了同类样本距离信息，但对于异类样本距离信息的利用仅限于最近邻的异类样本，异类样本距离信息的缺失使得LSC度量仅是对数据可分结构的局部表征量。

(3) Density

Density度量方法首先将数据表示成网图G=(V,E)的形式，网图G中的V表示样本，有节点数|V|=m，E表示样本连接边数，满足0≤|E|≤m(m-1)/2，同类样本xi与xj两两连接的条件是二者的距离小于给定阈值t，即d(xi,xj)

式(3)表明Density数值取决于网图G中保留的边数|E|，值越大表明数据越不可分。|E|的大小受到设定阈值t的影响，过大的t会产生近乎全连接结构的网图，过小的t将产生稀疏结构的网图，二者都将导致数据可分性判定的模糊。此外度量Density只利用了同类样本的距离信息，其表示同类样本紧密度，忽略了异类样本距离对数据可分性的影响，因而对异类样本距离变化不敏感。

(4) DSI

式(4)表明度量DSI充分利用了同类及异类样本的距离信息，其对数据可分结构的描述更加全面，但文献[13]的实验表明该度量无法衡量决策边界的复杂度。

上述方法存在统一的缺陷，即其都基于对样本距离的计算，因此度量性能将会受到所选择的距离函数的影响[29]。例如欧氏距离不适用于衡量高维数据的距离，这将导致基于欧氏距离计算的度量值无法比较具备不同维度的数据集可分性优劣。最后需要说明的是为了方便比较，各度量经数值转换后的取值范围都在0～1之间，且数值越小，表明数据的可分度越高。

3 率失真函数

率失真函数源于信息论中的编码理论，它描述了在限定编码误差下对数据的最小编码率[19]。当编码误差服从高斯分布时，零均值数据的最小编码率具有易于计算的表达式[20]。率失真函数为

其中，数据X=[x1,x2,...,xm]∈Rn×m由具有n维特征的m个样本构成；ε为给定的编码误差量；最小编码率R(X)是关于数据X的率失真函数，具体表现为与X的协方差阵有关的对数行列式log2det(·)的形式，n阶单位阵In×n的引入保证了方阵满秩，其行列式不为零。log2det(·)的凹函数性质使得R(X)具有良好的优化特性。

此外，式(5)同时具有较好的几何可解释性，可以作为数据所在特征空间的紧性度量。原始数据X在其特征空间的容量 vol(X)，正比于其正交的奇异向量组[σ1e1,σ2e2,...,σnen]所张成空间的体积，在数值上转化为数据奇异值σj的乘积，又等价于其协方差阵XXT的特征值λj的开方的乘积，如式(6)

式(8)反映了率失真函数的几何意义，即数据的奇异向量所张成空间的体积可以由多维高斯分布单元填充的数量表示，二维数据的率失真编码示意图如图2所示，其中高斯分布单元的半径应当小于数据的最短主轴，有

图2 二维数据的率失真编码示意图Fig.2 Schematic of 2D data’s rate distortion coding

4 基于率失真理论的数据可分性度量构建方法

4.1 单一维度的数据可分性分析过程

图3 不同奇异值下的数据可分性示意图Fig.3 Schematic of data separability under different singular values

4.2 高维数据可分性度量构建方法

将单一维度的数据可分性分析判别式向原始多维数据扩展，一个简单的思路就是将各个维度的可分性分析过程级联，由于数据的奇异向量相互正交，因此各个维度的可分性信息互不串扰，多维正交基下的数据可分性度量构建流程如图4所示。

由 log det(·)的凹函数特性，可以证明度量M的取值边界，其达到上界的充要条件为各类别的中心化数据具有完全相同的协方差阵，有定理1。

对于零均值多维高斯分布数据，当且仅当各类别协方差阵相等时，此时各类别数据具有完全相同的分布，数据处于完全不可分的状态，度量M越趋近于1，数据越不可分。

4.3 非高斯分布数据可分性度量方法

由4.1节及4.2节，定义数据可分性度量的数学模型

文献[30]在运用主动学习方法识别合成孔径雷达目标数据集时，首先给出了如图5原始数据X所示的样例。原始数据X中，目标X1与X2在总的特征分布上具有较高的相似性，对于仅能产生线性超平面的分类器，该数据是完全不可分的数据集，运用上述度量也将相应得出M ≈1的结论。但数据X中，不同类样本间的特征互不交叠且具有清晰的分隔边界，这意味着数据是局部可分的，对于能产生非线性分隔平面的分类器，该数据是完全可分的数据集，因此数据的局部可分特性影响了非线性分类器的识别性能上限。本文提出非高斯分布数据可分性度量方法，考虑了数据局部可分特性，能够真实地反映数据特征的重叠度，图5为在仿真样例的可分性度量模型构建示意图。

图5 非高斯分布数据可分性度量构建示意图Fig.5 Construction schematic of data separability measure under non-Gaussian condition

对于具有任意类别数的数据集可分性度量过程总结如算法1所示。特别地，当高斯聚类数k=1时，算法的子过程退化为典型二分类高斯分布数据的可分性分析情形，此时多分类数据的可分性度量值为各二分类度量模型的加权求和，类似于机器学习分类器的一对一(One vs One,OvO)模型，本节所提度量更关注数据中属于不同类别的样本间的局部可分特性。

5 实验验证

为验证所提度量的有效性，本文首先在二维仿真数据集上开展实验，二维数据可分性的特点在于其能够通过绘制特征散点图的方式直观地判定，因此当可分性度量值与直观判定的可分性优劣相当时，认为度量有效衡量了数据可分性；此外，加噪数据可分性可以由仿真设置的信噪比预先判定，因此当可分性度量值的变化趋势随信噪比增大逐渐减小时，认为度量有效衡量了加噪数据可分性。接着在实测高维数据上开展实验，由于高维数据可分性是非直观的，因此通过分析度量与不同模型统计得到的平均识别率之间的相关性来验证度量有效性，该实验的目的在于运用可分性度量量化数据识别难度，为评估识别模型在批量数据集上的识别能力提供评判基准。最后运用可分性度量量化分析了卷积神经网络各模块提取特征可分性变化趋势，进一步将所提度量作为特征可分性损失参与网络训练过程，达到优化特征质量的目的。上述实验中，现有可分性度量DSI,N2,LSC和Density方法作为对比方法体现所提度量的优势。

算法 1 平均意义下的数据可分性度量计算过程Alg.1 Average data separability measure computing

5.1 可分性度量有效性验证实验

由可分性度量方法评定的数据可分性优劣首先应当与现实可观察的数据可分程度吻合，因此该节实验主要验证可分性度量在已知可分性优劣的二维仿真数据与加噪数据上的有效性。二维数据可分性可以通过可视化其特征散点图的方式直观地判定，因此本文构造了不同可分性优劣的数据集，其特征散点图如图6、图7、图8所示。图6所示数据理想的决策边界复杂度由图6(a)-图6(f)依次递增，对应可分性依次递减；图7、图8所示数据的类间重叠度由图7(a)-图7(d)、图7(e)-图7(h)、图8(a)-图8(d)依次递增，对应可分性依次递减。图7与图8的区别在于类内样本是否能够用同一个高斯分布表示，以检验度量方法对非高斯分布数据的适用性。加噪数据可分性可以由仿真设置的信噪比预先判定，设置信噪比范围为-5 dB 到15 dB。

图6 二维数据特征图Fig.6 2D data’s feature map

图7 不同类间重叠度的高斯分布数据集Fig.7 Gaussian data with different class overlap

图8 不同类间重叠度的非高斯分布数据集Fig.8 Non-Gaussian data with different class overlap

5.1.1 决策边界复杂性度量验证实验

具体地，依据图6所示特征散点图，可以观察到数据图6(a)可以由一个简单的线性超平面正确划分开，数据图6(b)-图6(f)的理想划分面则需要更多线性超平面拟合得到，其不规则程度相对线性超平面而言依次递增，因此各数据集的识别复杂度是由图6(a)-图6(f)依次递增的。当可分性度量值由数据图6(a)-图6(f)顺序递增时，认为度量能够有效衡量各数据集的可分性优劣。依次设置高斯聚类数k1=k2=[1,3,5,8]，则所提度量及对比方法在图6所示数据的度量值总结如表1所示。

表1 典型特征图可分性度量结果Tab.1 Separability measure results of typical feature

表1中，标灰的度量值表示对应行的度量方法无法有效衡量对应列数据的可分性。具体地，对于图6所示的数据集，度量DSI无法区分数据图6(b)与图6(c)，这是由于其对决策边界复杂度不敏感[12]；度量N2及Density则无法区分数据图6(d)与图6(e)，这是由于从样本局部可分性的角度，度量N2认为图6(d)中包含有更多与异类样本更接近的样本，度量Density则认为图6(e)中同类样本分布更加紧密，从而得出了与判定决策边界复杂度相反的结论；所提度量在k=1时主要衡量数据线性可分度，表明图6(c)-图6(f)均为线性不可分数据，在k=3时利用数据局部线性可分度信息还不够充分，因此仍无法区分螺旋形与混合形数据，上述表明仅利用样本局部可分性的度量方法对数据整体可分结构的描述还不准确。实验表明仅度量LSC与(k>3)能够有效对比图6数据集的可分性优劣，这是由于度量LSC更关注决策边界附近的样本，而随着聚类数k的增加，所提度量对各数据集可分性优劣对比结果趋于稳定，其通过数据高斯分块的方式，结合基于率失真理论构造的可分性度量M，统计局部线性可分度，实现对数据全局非线性可分度的评估。

5.1.2 类间重叠度度量验证实验

制约分类器识别性能的因素之一是数据类间重叠度。图7、图8展示了不同类间重叠度的二分类数据集，每个数据由几族高斯分布采样2000个样本得到，类间重叠度则通过设置标准差σ或类中心距离µ调节，共同构成待评估数据集合。图7的数据集类内样本服从典型高斯分布，图8数据集的类内样本则呈现混合高斯分布的形式。对高斯分布数据设置两组实验，分别设置标准差σ ∈[1:1:9]与类中心距µ∈[0:0.5:4] ；对非高斯分布数据，设置σ ∈[0.1:0.1:0.9]。运用度量M,(k1=k2=4)及现有对比方法，度量结果如图9(a)、图9(b)、图9(c)所示。

图9 不同类间重叠度的数据可分性度量结果Fig.9 Separability measures for datasets with different class overlap and dimensions

图9(a)中，各可分性度量值均随着类间距的增加逐渐下降，变化趋势均符合观察到的事实：类中心距越远(µ越大)，类间重叠度越小，数据越可分。但各方法在该测试样例上的动态变化范围各不相同，可以看到当两类目标完全重叠(µ=0)时，度量M,DSI,N2,LSC均等于1，达到其上界，代表数据最不可分的情况，而Density等于0.765，取值无法反映最不可分数据集的可分性。当µ由0增加到1.5时，类间重叠度显然减小，对应到LSC上却没有明显的变化趋势，而N2在µ由0增加到0.5时出现了陡然的下降趋势，但此时类间重叠度变化是微小的。图9(b)中，LSC在σ=6时取值为1达到其上界，但由图7(g)数据此时还不是完全不可分的；其余可分性度量值均随着类内分散度的增加而逐渐上升，变化趋势均符合图7观察到的事实：同类样本越分散(σ越大)，类间重叠度越大，数据越不可分。在图9(a)、图9(b)实验中，仅M与DSI在两类目标由完全重叠到完全分离过程中，表现出最大动态变化范围，且变化趋势更加平滑。图9(c)中，仅M,DSI,N2随σ增加而逐渐增大，但DSI将未交叠非高斯数据(图8(a))判定为可分性很差的数据集，度量值为0.75，但事实上对于K近邻等能产生非线性决策边界的识别器而言，该数据集是完全可分的。

在上述3个实验中，LSC无法区分类间重叠度已经达到一定量级的数据可分性；Density更多衡量同类样本紧密度，因此在图9(c)中由于同类样本随σ增加逐渐靠近，从而在数值上表现出可分性渐好的趋势；仅M,DSI,N2随着不同类样本交叠量的增加均表现出正确的变化趋势；但DSI无法衡量具有非线性划分结构数据的可分性；所提度量M具有更大的动态变化范围，且相对N2更加平滑(图9(a))，能够有效衡量高斯或非高斯数据的类间重叠度。

为进一步解释所提度量M的工作机理，图10给出图7实验场景中作为M分子的类内分布散度Mnum和作为分母的整体分布散度Mden的变化趋势。图10(a)表明当µ变 化时，Mnum保 持恒定，Mden起到主要的可分性度量作用，说明整体分布散度中包含数据的均值差异信息；图10(b)中随着σ的增加，Mnum与Mden同时上升，Mden逐渐逼近Mnum，对应类间重叠度增加，表明Mnum与Mden的相对数值能够有效衡量数据类间重叠度。

图10 整体分布散度与类内分布散度变化趋势Fig.10 The trend of overall and intra-class distribution divergence

5.1.3 加噪数据可分性度量验证实验

本节实验模拟真实目标识别噪声环境，通过将模型训练在原始数据测试在批量加噪数据上以评估其性能，同时验证度量在加噪数据上的有效性。理想的识别模型是其在所有加噪数据上的识别率都一致高于其他模型，但在实际性能比对实验中，更一般的现象是模型在不同加噪数据上的识别率各有高低，这导致性能评估模糊问题。以表2中数据WDBC为例，构造信噪比-5 dB 到15 dB的加噪数据，SVM(RBF),KNN,LSVM,LR的识别率结果反映了上述问题，如图11。

表2 识别模型识别率结果Tab.2 Recognition accuracy results of recognition models

图11 不同信噪比条件模型识别率表现Fig.11 Different models’ accuracy under various condition

图11中KNN在各信噪比数据上的识别率一致地高于LR，而LR又一致地高于LSVM，可以得出三者抗噪性能的对比结论：KNN >LR >LSVM。但由该图无法得出SVM(RBF)的性能评估结论，SVM(RBF)在信噪比高于3 dB时一致地优于其他模型，信噪比低于-2 dB时性能最差。虽然可以通过对比各信噪比数据上的平均识别率来判定模型性能优劣，但平均识别率忽略了各数据集的识别难度差异，直观上更难识别的任务应当被赋予更大的权重，因此通过可分性度量量化识别难度，为识别率赋权提供依据，加噪数据可分性度量结果如图12。

图12 加噪数据可分性度量结果Fig.12 Separability measure results of noisy data

图12中仅Density数值随信噪比上升存在微弱的起伏，说明其度量精度较差。DSI虽具有最大动态变化范围，但图11中大部分模型的识别率变化趋势缓慢，说明各任务间识别难度差异并不十分显著，且当信噪比为 15 dB时模型识别率与表2中在原始数据的测试结果还存在一定差距，说明此时可分性数值也仍存在一定差距，但DSI数值已经接近对原始数据可分性度量结果0.5833。所提度量M具有合适的动态变化范围，且信噪比为15 dB时值为0.4352，与原始数据度量值0.2497还存在一定差距，综合表3的实验结果所提度量M更能真实地反映数据可分性。

表3 实测数据集可分性度量结果Tab.3 Separability measure results of real data

5.2 基于可分性度量的数据识别难度评估实验

在数据集发布与构建相关的文献[31,32]中，通常运用公开通用的识别模型如支持向量机、经典深度神经网络架构等检验构建数据集的适用性，用识别结果分析数据可分性。然而使用的识别模型不同，识别结果存在明显差异，无法描述数据固有可分特性，因此本节基于可分性度量评估数据识别难度。此外数据识别难度评估的需求还源于目标识别评估中的具体问题：如何从在各个识别任务上识别率各有高低的众多识别器中选出识别性能最优的模型。为直观展现上述问题，本节选择4种识别器：运用径向基核函数(Radial Basis Function,RBF)的支持向量机(Support Vector Machine,SVM)、K近邻(K-Nearest Neighbors,KNN)、线性SVM和逻辑回归方法(Logistic Regression,LR)，在表2所示的14个二分类实测数据集上[25]测试模型，测试过程中训练集与测试集按照7/3的比例划分。表2给出数据集样本总数、相应的正负例数及特征数，各模型在各数据上的识别率，“√”表示其在对应行数据上识别率最高，“×”表示最低，平均识别率为4种识别器在同一数据上识别率的平均值，文献[6]表明其可以作为侧面反映识别难度的参考值。

表2首先可以直观地反映以下问题：(1)同一种模型在不同数据上的识别率各不相同，变化的识别率无法作为衡量模型识别能力的固有属性。(2)不同模型在同一数据上的识别率各不相同，且有时会出现较大差距，如 LSVM在Hill valley上的识别率为0.9670，而SVM(RBF)为0.4780，变化的识别率无法作为衡量数据识别难度的固有属性。(3)平均识别率在一定程度上可以反映数据识别难度，但其有效性基于运用大量识别器开展统计实验，并且无法客观描述样本数分布不均的数据集如Blood,ILPD,Haberman的识别难度。(4)在不同数据上模型识别率高低对比结果各不相同，如SVM(RBF)在Banknote,Ionosphere,Magic,Blood上识别率最高，而在Wisconsin,Fire,Hill valley上识别率最低，导致无法得出统一的性能优劣评估结论。

为解决依赖识别率评估产生的性能比对模糊问题，考虑到数据固有可分特性对识别性能的影响，本节利用可分性度量方法评估数据识别难度，由量化的识别难度为识别任务标定基准，进一步可以考虑构建以识别难度为参数的识别率到模型识别能力的函数映射模型，得到表示模型固有识别性能的固定表征量。本文工作重点在于验证所提度量方法的有效性，14个数据集可分性度量结果如表3所示，其中平均错误率作为参照指标之一，各指标值越大表示数据越不可分。在排除样本数分布不均的数据集Blood,ILPD,Haberman后，平均错误率作为不同模型对同一数据识别结果的统计量对可分性的衡量具有一定的参照意义，因此通过分析各度量值与平均错误率之间的相关性验证度量有效性，绘制各度量值与平均错误率之间的皮尔逊相关系数如图13，同时绘制度量与平均错误率曲线图如图14。

图13 可分性度量与平均错误率相关性矩阵Fig.13 Correlation matrix between separability measures and average recognition error

图14 可分性度量与平均错误率曲线Fig.14 Curves between separability measure and average recognition error

相关系数的取值在-1到1之间，取值为正表示变量之间是正相关，为负表示负相关，其绝对值越大表示变量之间的线性相关性越强。图13中，所提度量M与平均错误率的相关系数为 0.96，具有最大的线性正相关性，表明随着M逐渐增大，数据变得越来越不可分，对大多数识别器而言识别性能下降，错误率随之提升。表现最差的度量为Density，其与错误率的相关系数为-0.12，说明同类样本紧密度并不足以衡量可分性。LSC,N2,DSI与平均错误率仍具有一定的正相关性，相关系数值分别为0.66,0.67,0.73，说明其也具备一定衡量可分性的效能，因此对于样本数分布不均的数据，则可以通过比对M与N2,DSI的判定结果来分析M是否有效。例如表3中样本分布不均的Haberman数据，平均错误率已不能客观反映其与Mammographic的可分性差异，但通过与LSC,N2,DSI对照，表明M仍能够正确地判定Haberman为可分性较差的数据集。图14中，所提度量M数值与平均错误率基本对应，越小的M代表识别难度越小，对应低平均错误率；对比方法均存在较大的振荡幅度，而M仅在数据Spambase和Sonar之间出现微小的振荡，说明二者的识别难度相当，而平均识别率的统计误差导致了这一现象。

相较于依赖大量模型统计识别结果的错误率指标，所提度量M独立于模型识别过程，对数据固有可分特性描述更加本原，度量值更加客观。此外在计算量上M相较对比方法也具备突出的优势，对于具有m个样本的n维数据，M的计算量在于两次协方差阵行列式的计算，协方差阵的规模为n×n，当m>>n时如表3数据Magic，对比方法则需要建立19020×19020的距离矩阵而带来巨大的存储负担，且导致运算效率低下，M则只需要计算两次10×10规模矩阵的行列式，在存储空间和运行时间上都大大优于对比方法。

5.3 基于可分性度量的识别网络特征质量评估实验

深度学习识别模型具有提取数据高维可分特征的能力，本节实验首先探究深层卷积神经网络中，随着网络层次的加深及训练轮次的迭代，各卷积层所提取特征可分性与模型识别率相对应的变化趋势特点，从特征可分性角度定量化解释神经网络有效工作的原因。进一步地，本节将所提可分性度量作为网络损失函数的一部分，优化网络学习到的特征质量，探究特征可分性对提升网络识别性能的实质性作用。

本节采用合成孔径雷达(Synthetic Aperture Radar,SAR)图像数据集，包含标准工作条件下的MSTAR数据集[33]和复旦大学发布的FUSAR数据集[32]。其中本文构造的三分类FUSAR数据集包含样本量较多的货船、渔船和其余船只目标，3类船只包含相同的训练集样本量，以保证训练过程的类平衡性。表4总结了SAR数据集相关参数。

表4 SAR图像数据集Tab.4 SAR image datasets

本节首先在MSTAR数据集上评估文献[34]提出的卷积神经网络模型，网络结构及可分性分析模块如图15所示。其中原始SAR图像经过4个卷积模块映射到可分的特征空间，为了减小可分性分析的计算量，在张量展开步骤之前对映射特征统一采用了2 ×2的自适应平均池化操作，最终各层得到的特征维度分别是64,128,256及512维 。网络在MSTAR测试数据集上的识别率acc如图16所示，经卷积模块所提取特征的可分性度量结果分别如图17所示，图17由左至右分别是模块1至模块4提取特征可分性分析结果和各层可分性对比结果，由上至下分别对应Density,DSI,LSC,N2,M度量方法。

图16 网络在MSTAR数据上的识别准确性能Fig.16 Recognition accuracy performance of the network on MSTAR datasets

图17 MSTAR数据集特征可分性度量结果Fig.17 Feature separability measure results for MSTAR dataset

由图16仅能得出网络在MSTAR测试数据上以较少的训练轮次就达到了较高的识别率，但无法从中解释神经网络有效工作的具体原因，因此将各模块提取特征可分性评估引入识别评估过程。图17可以得出模型之所以在输出端表现出优异的识别性能是由于组成神经网络的各个模块都提取到了逐渐可分的目标潜在特征，在实验现象上表现为随着网络深度的增加，所提取特征均呈现越来越可分的趋势，数值上有ML1>ML2>ML3>ML4，并且随着迭代轮次的增加，特征可分性渐高，预示着识别率的提升；特征可分性收敛，预示着识别率的饱和。图17同时比对了本文所提方法与对比方法对特征可分性的度量结果。Density的度量性能最差，随着训练轮次的增加，各层度量值呈现发散的趋势，且无法区分第2～4层特征可分性优劣；其余方法均能够区分各层特征可分性的优劣，数值上表现为DSIL1>DSIL2>DSIL3>DSIL4,LSCL1>LSCL2>LSCL3>LSCL4,N2L1>N2L2>N2L3>N2L4，可以体现越深层网络提取的特征越可分，但所提度量M相比对比方法具有更加平滑的收敛趋势，且各层可分性度量值的数量级差距更大，说明M对特征可分性的变化更为敏感。从模型性能优化的角度，将M作为损失函数的一部分，迭代过程中同时优化特征可分性，能够快速引导模型学习到更加可分的特征，从而提高模型识别性能。

进一步地，本节在文献[35]提出的骨干网络中加入特征可分性度量损失，在FUSAR数据集上探究所提可分性度量对网络识别性能提升的实质性作用。带有特征可分性度量约束的卷积神经网络组成如图18，其中包含用于特征提取的卷积模块、卷积注意力模块(Convolutional Block Attention Module,CBAM)、全连接模块，用于特征融合的平均特征融合模块，以及用于评估特征质量的特征可分性评估模块。网络损失函数由评估预测标签与真实标签差距的交叉熵损失和评估特征质量的可分性损失构成。考虑到识别性能与网络各层特征及融合层特征都密切相关，故损失函数L有式(17)与式(18)两种方案。

图18 特征可分性度量约束下的卷积神经网络Fig.18 Convolutional neural networks with feature separability constraints

其中，LLabel表示交叉熵损失，Mfi,Mfavg的形式如式(11)，分别表示第i个特征提取模块的特征fi与平均特征favg的可分性度量，favg为fi(i=1,2,...,5)的平均值，α,β为可调比例系数。式(17)与式(18)两种训练方案在训练集上交叉熵损失表现如图19，在测试集上的识别率表现如图20。

图19 训练集上交叉熵损失表现Fig.19 Cross-entropy loss performance on the training set

图20 测试集上的识别率表现Fig.20 Accuracy performance on test set

图19中，α=β=0表示训练时不加特征可分性约束的基准网络在训练集上的损失函数表现，可以看到随着可分性比例系数α或β逐渐增加，训练集上的交叉熵损失以更快的速度收敛到了更低的值，增强了对训练数据预测标签与真实标签之间的拟合效果。此外对比方案1与方案2的性能，当α或β均较小时，二者性能相当，交叉熵损失曲线基本重合；随着α与β逐渐增加，相同比例系数的方案2相较方案1对训练集具有更好的拟合效果。图20展现了两种方案在测试集上的识别率表现，可以看到当α或β取0.01,0.10或0.25时，识别率曲线在训练初期(10～30轮次)能够相较基准网络达到更高的识别率，且α或β越大，提升效果越明显。当α或β取0.50时，识别率曲线出现了明显的振荡，但在整个训练过程中最高识别率相对基准网络仍有明显的提升。此外对比两种方案的性能，方案1在α=0.50时，第37轮达到了82.36%的识别率，方案2在α=0.25及α=0.50时分别在第37轮及第98轮达到了80%的识别率。而在训练的收敛阶段(60～100轮次)，方案1相较方案2在α=β=0.50时能够相较基准网络有明显的识别率提升。上述表明方案1在测试集上的泛化性能优于方案2，将网络各层特征可分性度量作为损失函数的一部分对特征可分性加以约束，能够优化网络训练过程，并且改善网络在测试集上最终的识别率表现。表5给出不同α与β数值下的两种方案在测试集上最优识别率表现，对应给出训练集上的识别率。其中随着α或β的增加，训练集识别率均有不同程度的提升，方案1在训练集上拟合性能虽稍劣于方案2，但其在测试集上泛化性能明显优于方案2，具体表现在方案2β=0.50的测试识别率相对基准网络约有0.91%的提升，方案1α=0.50时则有3.27%的提升。

表5 不同可分性系数下最优识别率表现(%)Tab.5 Optimal accuracy performance with different separability factors (%)

此外可分性度量对网络识别性能的提升不仅体现在识别率上，还体现在其能够引导网络提取到更可分的特征。从可视化的角度分析特征可分性，本节采用样本间余弦相似度矩阵及t分布随机近邻嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)，其中余弦相似度矩阵图的行列表示样本索引，已按照样本所属类别排序，两个样本余弦相似度越大表示二者越相似。图21与图22分别给出表5中基准网络与α=0.50的可分性约束网络最终层提取特征的样本间余弦相似度矩阵及t-SNE图。可以看到相对基准网络，α=0.50时训练集和测试集上类内样本余弦相似度都有显著的提升，而类间样本余弦相似度虽然在第37轮迭代中没有理想的下降趋势，但在图21(b)的训练集中其数值显著小于类内相似度，相较图21(a)，类间与类内相似度比值存在下降趋势，从而提升了特征可分性。而图21(d)测试集上的可分性改善还在一定程度上受其与训练集模板相似度的影响，因此对特征可分性优化效果不如图21(b)显著。由于t-SNE降维方法倾向于聚合相似度较高的样本，图21也表明加入可分性损失后，类内样本相似度普遍高于类间样本，因此在图22(b)与图22(d)中更为相似的类内样本优先被聚合，从而表现出更高的类内聚集形式以及更加清晰的理想决策边界。通过本实验表明所提度量能够有效地衡量网络提取特征变化趋势，将特征可分性度量作为网络损失函数的一部分进行优化，能够快速引导网络学习到更可分的特征，从而提升识别性能。

图21 最终层输出特征样本间余弦相似度矩阵Fig.21 The cosine similarity matrix between feature samples output from the final layer

图22 最终层输出特征t-SNE图Fig.22 The t-SNE visualization of the feature output from the final layer

6 结论与展望

数据可分性度量为分析和评估识别模型性能提供了一种基准，在赋予了数据可分性的条件下，更能客观地评价识别模型性能。本文基于率失真理论构建可分性度量模型，其描述了数据整体分布散度与类内分布散度的相对关系，综合了样本分布在各个正交特征维度的可分性信息。实验表明，设计的度量方法通过结合高斯混合模型能够衡量非高斯数据可分度；所提度量可以比较具备不同维度的数据集可分性优劣，其数值与经不同模型统计得到的平均识别率有强相关性，能够作为数据识别难度的量化值，为识别结果预先提供评判基准；并且能够评估神经网络各卷积模块提取可分特征的贡献度，在测试阶段作为网络提取可分特征的评估指标，在训练阶段作为网络提取可分特征的优化指标。

本文是对数据可分性研究的初步探索，仍有许多值得进一步深入开展的研究工作，包括针对具体识别任务特性与考虑数据更多分布特性的可分性度量设计，探究可分性度量与识别性能上限的对应关系，解释识别网络各层特征可分性之间的关联等。总的来说，数据可分性度量作为直接面向数据的评估指标，与面向模型的准确性指标相结合，为雷达目标识别评估提供了一个新的评估视角，对识别模型实用化改进具有指导性意义。