沪铜期货价格波动的影响因素分析

刘超奇

（浙江工商大学，浙江 杭州 310000）

一、引言

铜是人们广泛运用的一种金属材料，具备良好的物理和化学性质。铜期货是以铜作为标的物的期货品种，国内的铜期货在上海期货交易所上市。上海期货交易所的铜期货自1991年推出以来，历经了30年，仍能保持较大的发展规模，也未曾发生重大交易风险，履约率达100%，因此，上海期货交易所铜期货价格已经成为国内行业的权威报价，其重要性不言而喻。所以，研究铜期货价格波动的影响因素，对于进一步分析铜期货所面临的风险，从而采取适当策略加以控制和管理风险，对于投资活动以及相应政策的出台具有重要的现实意义。

二、文献综述

（一）波动率建模综述

美国经济学家、2003年诺贝尔经济学奖得主Engle（1982）率先运用自回归条件异方差（ARCH）模型研究英国通货膨胀率的波动，此模型假定，当期收益的随机误差项的方差有前期收益的随机误差项决定，因此，非常适合波动率聚集现象的产生。美国芝加哥大学学者Nelson（1991）通过建立指数GARCH（EGARCH）模型，将模型中条件方差对数化，使得无需对参数加以限制来确保模型中条件方差的非负性，从而弥补了GARCH模型的缺陷。

为了有效刻画长记忆性的经济或金融现象（金融时间序列的绝对值自相关性衰减非常缓慢，即在时间间隔很远的情况下依然具有较强的自相关性），我国专家张世英和柯珂（2001）提出分整增广GARCH-M模型，从而克服了ARCH模型在描述这一方面遇到的困难。

（二）商品期货或现货价格波动综述

宏观经济形势是影响商品价格的最重要因素之一，也是学界研究的热点。新西兰学者Watkins 和澳大利亚学者McAleer（2008）通过构建对数周期AR（1）-GARCH（1，1）AR（1）-GARCH（1，1）模型对铝、铜、铅和锌的期货价格波动行为进行模拟。结果表明：宏观经济因素对有色金属产业造成的影响可能比某些特殊事件对有色金属产业造成的影响更大。货币的利率与汇率是宏观经济的重要指标。

其次，国家的财政政策、货币政策也是宏观经济的重要组成部分。意大利银行经济部门学者Anzuinie（2010）通过构建向量自回归模型（VAR模型）对于美国联邦基金利率和货币供应量对于大宗商品价格的影响进行分析。结果表明：基金利率的下降会促使大宗商品价格的提升，而货币供应量对于大宗商品的价格的影响程度相对较小。

一些经典指标如工业增加值、通货膨胀率等，都是宏观经济的重要组成部分。我国学者邵威豹和崔寅生（2011）通过构建VAR模型研究了2007年1月至2010年5月的农产品价格的数据，通过引入对应时间的货币供给量、通货膨胀率以及产品贸易额来研究以上变量对于农产品价格波动的影响。结果表明：通货膨胀会对农产品的价格波动产生影响，但农产品贸易与货币供应量对于农产品价格的波动影响不大。

通过对以上文献的分析与研究，本文在基于ARMA-GARCH模型拟合铜期货日收益率和条件波动率的基础上，引入中国工业增加值、人民币兑美元汇率和广义货币（M2即狭义货币 M1加商业银行定期存款的总和）月度数据，通过VAR模型分析铜期货价格波动的影响因素。

三、模型设定及分析

（一）数据准备

本文从同花顺iFinD数据库选取了2019年11月29日到2022年11月29日的上海商品期货交易所的沪铜连续期货价格作为数据基础。根据结算价的对数差分算出铜期货多头的对数收益率。

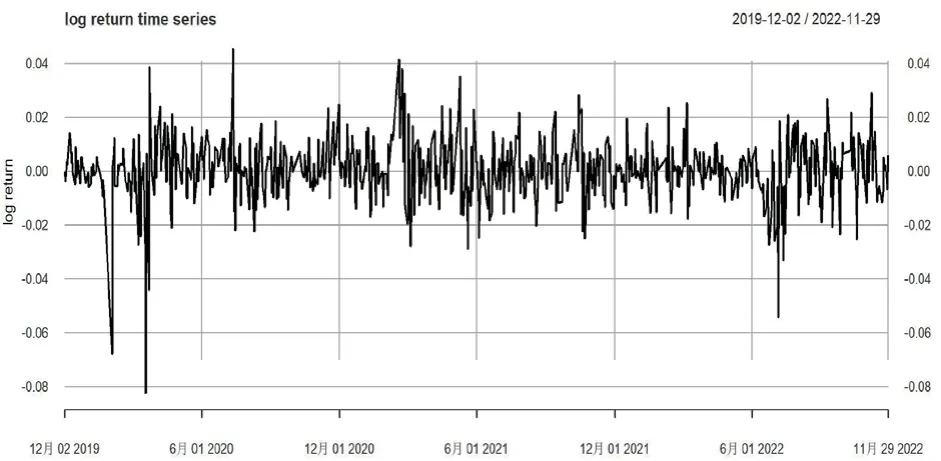
图1 对数收益率的时间序列图

（二）模型设定前期准备

本文通过ADF（Augmented Dickey-Fuller）检验来研究获取的对数收益率时间序列是否平稳。根据表2数据显示，ADF检验的p值为0.01，说明该时间序列平稳，能够直接进行时间序列建模。对于均值的t检验，无法拒绝原假设，说明均值为0。

表1 ARMA-GARCH模型回归结果

表2 各个变量的平稳性ADF检验

（三）运用ARMA-GARCH模型拟合收益率

1.ARMA（自回归移动平均模型）定阶

基于AIC的优良性质，本文采用AIC判断准则进行模型的定阶。经过运算，发现MA（2）模型的AIC值最小，为-4454.417，因此，本文用不带截距项的MA（2）模型来拟合对数收益率。

2.建立ARMA-GARCH模型

在MA（2）的基础上建立GARCH（1，1）（广义自回归条件异方差模型）模型进行拟合。运用均方误差对比残差服从不同分布的预测效果，发现残差服从有偏的t分布时模型的均方误差和平均标准误差最小，因此，残差设定为服从有偏的t分布。

3.检验ARMA-GARCH模型

为了检验ARMA-GARCH模型是否满足基本要求，对模型拟合结果的残差和残差的平方进行Ljung-Box检验。结果为p值都大于10%。

通过残差的自相关性检验可以看出，对数收益率的ARMA-GARCH模型的残差都具有白噪声的性质；通过残差平方的自相关性检验可以看出模型都不存在显著的ARCH效应。

（四）VAR（向量自回归）模型分析沪铜期货波动的影响因素

1.数据准备

图2 残差服从于有偏学生t分布的ARMA-GARCH模型拟合的条件波动率时序图

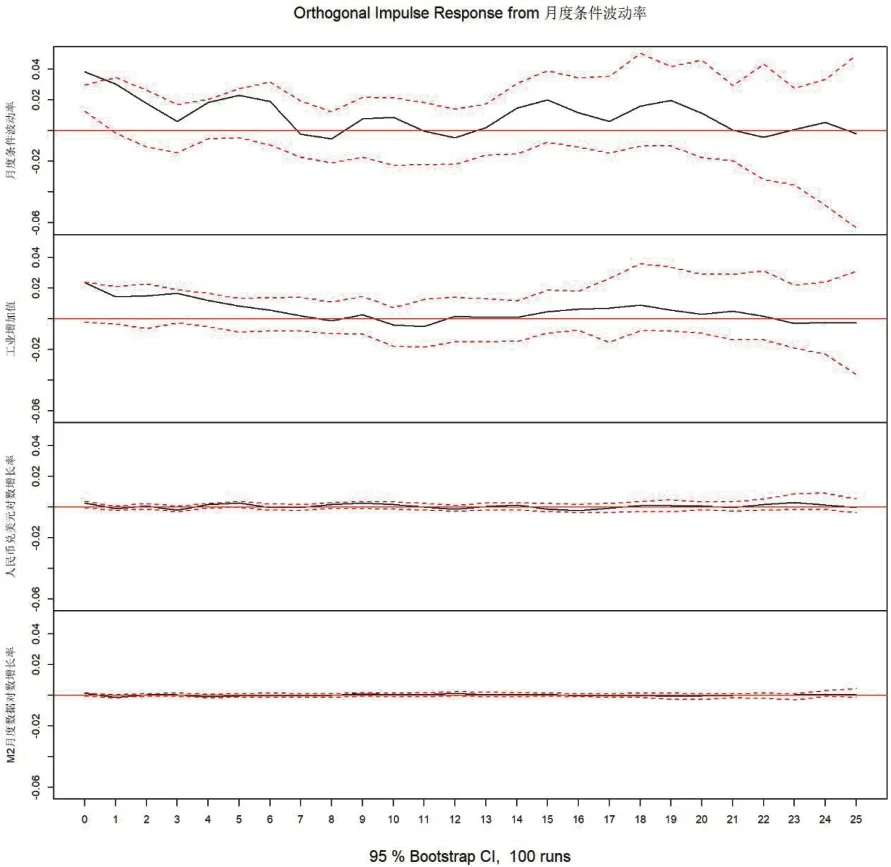
图3 VAR模型条件波动率的脉冲响应图

下面检验各个变量是否平稳。对以上四个变量进行包含趋势项和漂移项的ADF检验，对工业增加值进行含有漂移项的ADF检验。结果是4个变量都能保持平稳。

2.建立VAR模型

本文采取比较阶数的信息准则来确定含有趋势项的VAR模型的阶数。通过将最大阶数设为5，发现阶数为5时，信息准则AIC、HQ和FPE能够达到最小值。所以，最终确定带截距项的VAR模型阶数为5。

通过设定带趋势项的模型阶数为5，本文利用OLS（最小二乘法）方法估计VAR模型的参数。模型R2为99.09%，拟合较为充分，且模型的大多数参数和整体为显著，整体的P值为8.91×10-7。

3.VAR模型检验

（1）平稳性检验

本文通过模型特征根是否落在单位圆内进行检验VAR（5）模型是否平稳。由数据可知，最大的单位根为0.9833，因此，所有单位根均落在单位圆内，说明该模型平稳。

（2）残差序列相关检验

为了检验VAR（5）的各个变量的残差是否具有序列相关性，本文进行Ljung-Box对残差的序列相关性进行检验，结果如表3所示。

表3 VAR模型各变量残差序列相关检验结果

通过对模型各变量残差的序列相关检验，可以得出改模型的各变量残差都不存在序列相关，说明残差为白噪声，因此，该VAR（5）模型在此方面具有良好的性质。

4.脉冲响应

脉冲响应分析用于展示随时间变化的离散时间或瞬时数值。常用于比较事件的频率、强度或持续时间等特征。

为了分析各个变量对于条件波动率在各个期数影响的详细状况，本文进行25期的脉冲响应分析。结果如图3所示。

由图3可知，月度波动率对月度条件波动率的冲击最大，其次是工业增加值，M2月度数据对数增长率对月度条件波动率的冲击最小。月度条件波动率对自身的冲击在当期达到最大，此后的期数一直在0附近徘徊，第2期开始有负冲击；工业增加值对月度条件波动率的冲击在当前时刻达到顶峰，在第8期开始出现负冲击，此后一直衰减到0左右的位置。

5.方差分解

方差分解描述了对VAR模型中的变量产生影响的每个随机扰动的相对重要性的信息。为了清楚分析4个变量对于条件波动率变化的贡献程度，本文进行方差分解；同时为了更加准确刻画影响趋势，本文将期数设定为150期，结果如图4所示。

图4 各变量对条件波动率的150期方差分解图

月度波动率随着时间推移，其对自身变动的贡献率逐渐降低，工业增加值对月度波动率变动的贡献率逐渐增加。到了第20期左右，月度条件波动率对自身变动的贡献率稳定在40%左右，工业增加值对月度条件波动率变动的贡献率稳定在15%左右。人民币兑美元对数增长率和M2月度数据对数增长率对月度条件波动率的变动的影响也是逐渐增大，分别在80和90期左右稳定在40%和5%左右。

四、结论及建议

（一）结论

从脉冲响应的结果来看，铜期货价格的波动率受到波动率自身和工业增加值的冲击较大，但随着期数的增加，波动率自身和工业增加值对铜期货波动的冲击会出现时正时负的震荡局面，到最后趋于收敛。因此，从短期看，工业发展能够显著促进铜期货价格的波动；而从长期来看，工业的发展对铜期货价格的波动的冲击会产生不确定性，这也能够体现出铜产品的波动较大的特性。

从方差分解的结果来看，波动率对自身方差的贡献随着期数的增加而递减，其余变量随着期数的增加总体呈上升趋势，人民币兑美元的对数增长率能够贡献的方差百分比能够达到最大，说明铜期货波动率的变化受到国际市场的影响较大。

（二）相关建议

稳定国际汇率以减小沪铜期货的波动风险。基于方差分解，可以发现铜期货与外贸市场有着较为密切的联系。因此，政策制定者需要稳定国际货币市场，保持汇率稳定，进而稳定铜期货波动率的变动，从而化解铜期货的外贸风险。

沪铜的生产者应频繁关注国际汇率市场、国内货币市场和国内工业的发展情况以及相关新闻，及时调整经营策略，如进行期货的套期保值以规避铜价的下降风险。沪铜期货投资者面对工业产值的提升应及时反应，抓住短期机遇。基于脉冲效应和方差分解可知，短期的工业增加值对于波动率的冲击效应更大，随着时间推进冲击会逐渐缩小，甚至产生负效应。因此沪铜期货投资者需要对国内工业的发展具有灵敏的嗅觉，抓住短期的工业对于沪铜期货价格波动率的正向冲击，从而能够选定合理时间买入或卖出。此外，沪铜投资者应着重分析沪铜期货价格的近期波动率。由于近期波动率对于当前波动率的影响程度更大，且关联程度较高，投资者应着重分析近期波动率的走势从而预测波动率未来的变化情况，进而做出合理的投资决策。