存在离群值情形下行业股票的风险特征分析

余 味

（安徽大学 大数据与统计学院，安徽 合肥 230601）

1 资本资产定价模型

资产定价是金融研究的核心问题。资产定价的常用方法有两种：均衡定价和无套利定价。均衡定价的思想与经济学中实物商品的价格决定机制类似，也就是寻找使得商品的供给和需求达到平衡时的价格。Sharpe[1］提出了资本资产定价模型，可以表示为

其中，Ri表示我们关注的风险资产i的收益率，RM为市场组合的收益率，rf为无风险利率，βi衡量资产的风险大小。按照此模型，不同资产的均衡价格满足一种线性关系，其超额收益率与风险系数βi成正比。风险系数用下式衡量：

其中，σiM表示资产i与市场组合的收益率协方差，σ2M表示市场组合收益率的方差。该模型揭示了资产风险的本质是资产收益率波动不能够被市场上其他资产对冲的部分，在表达式中表现为资产i与市场组合的收益率协方差。无论组合的资产种类如何增加，这部分风险都无法被分散，通常称为系统风险。而能够通过资产组合来分散的风险称为个体风险，二者之和就是总风险。因此资产i的风险溢价E(Ri)-rf就可以表示为“风险溢价=风险的度量×风险的价格”[2］，风险的度量是βi，而风险的价格是E(RM)-rf。

资本资产定价模型在金融实践中得到了广泛的应用，也有很多关于其有效性的讨论。申婧怡[3］基于CAPM 研究了2012年至2017年万科股票指数，通过回归模型判断该项资产的收益效果。张燕、王一登[4］利用CAPM 研究了不同牛市和熊市下证券商业股票市场的系统风险和总风险，验证了资本资产定价模型在证券行业的有效性，并且说明了系统性风险与总风险的关系在牛熊市存在差异以及分析了造成差异的可能原因。崔劲等[5］使用A 股上式公司的数据，发现小规模公司存在明显的超出CAPM 模型下期望报酬的规模溢价。Bai 等[6］在一般均衡模型中考虑灾害的影响，来帮助解释CAPM 模型的失效情形。Rubinstein[7］，Lucas[8］，Breeden[9］，Grossman 和Shiller[10］将资产价格与消费联系起来，建立了基于消费的资本资产定价模型（C-CAPM）。Choi[11］在考虑股票溢价的弱可预测性和无风险利率谜题的情形下，讨论了基于消费的资本资产定价模型所存在的问题和争议。

由于β系数对于资产的定价有重要意义，而且不同行业股票的β系数往往呈现不同的特征，这为我们分行业探讨股市走向提供了思路，而β系数的估计是一个技术性较强的线性回归问题。由于突发状况的影响，一些股票可能在某段时间出现大涨或大跌，导致股市数据经常会出现离群值。本文将分析使用实际收益率数据来估计资本资产定价模型时存在的问题，寻找数据存在离群值的情形下较好的估计方法，并用此方法来分析各行业股票的风险特征。

2 模型及其估计方法的比较

实践中我们通常使用线性回归模型来估计β系数。用R(j)*i=R(j)i-rf表示资产i的超额收益率，其中R(j)i,j=1,…,n表示资产i的收益率的n个观测值；R(j)*M=R(j)M-rf表示市场组合的超额收益率，其中R(j)M,j=1,…,n表示市场组合的收益率的n个观测值。 那么根据资本资产定价模型应该有但是用真实数据来拟合时，这种关系一般不会精确地成立。因此我们通常拟合的是含有截距项的模型，也就是

该模型是一般的线性回归模型

的一个特例。模型（4）中，α和β是待估参数，εj是扰动项，满足E(εj)=0 的假定。用(xj,yj),j=1,2,…,n表示一组观测样本，α和β的最小二乘估计是寻找,，使得残差平方和达到最小。然而，当样本存在离群值时，残差平方和增加得很快。离群值会将回归线极大地拉向自己，导致回归的结果不准确（图1）。

图1 离群值对回归直线位置的影响Fig.1 Effect of outliers on the position of regression line

为了解决参数估计中离群值的影响，将最小二乘估计量扩展为一般的M 估计量，其定义为求解如下的最优化问题：

其中ρ(·)是定义在(-∞,∞)的连续函数，满足ρ(0)=0，ρ(-u)=ρ(u)。

经典的最小二乘估计法实际上就是在（5）式中使用ρ(u)=u2。为了得到受离群值影响较小的估计结果，一个思路是使用其他的ρ(·)函数来替代平方损失函数。最小绝对值法使用ρ(u)=|u|.Huber[12］和Huber[13］使用如下的ρ：

Geman-McClure 方法（Pennacchi[14］）使用如下形式的ρ：

其他稳健估计方法还有Andrews 法（Andrews[15］），Hampel 法（Hample 等[16］），Tukey 法（Lee 等[17］），Danish法（Knight 和Wang[18］）等。下面我们将探讨稳健估计方法是否能够减小估计偏差。

在模型（4）中，设置α=2，β=1。xj从均值为10 的指数分布中产生，εj从标准正态分布中产生，然后根据模型计算出yj的模拟值。对于每一个模拟样本，按以下4 种情况构造离群点：

情形1：无离群点；

情形2：第5 个点的y值加上粗差10；

情形3：第5 个点的y值加上粗差10，第10 个点的y值加上粗差-10；

情形4：第5 个点的y值加上粗差20。

然后使用4 种方法来估计α和β——最小二乘法（记作LS），最小绝对值法（记作LA），Huber 法（记作Huber）以及Geman-McClure 法（记作GM）.对于Huber 法，设置其参数c=1.5。估计的过程就是求解（5）式的最优化问题，可以使用选权迭代法。

重复以上过程B次，得到B个和的模拟估计值(k),(k)，k=1,…,B。用平均绝对偏差来衡量估计量的准确性，也就是

考虑样本量为n=10,20,30,40,50。不同样本量以及离群值情形下模拟计算的结果显示在表1～4中。

表1 离群值为情形1时，不同样本量下4种方法的和估计的平均绝对偏差Table 1 Mean absolute error of the estimators α^ and β^ based on the four methods under different sample sizes when the outlier is in case 1

表1 离群值为情形1时，不同样本量下4种方法的和估计的平均绝对偏差Table 1 Mean absolute error of the estimators α^ and β^ based on the four methods under different sample sizes when the outlier is in case 1

MAE(α^)MAE(images/BZ_6_1250_1625_1276_1679.png)n=10 n=20 n=30 n=40 n=50 n=10 n=20 n=30 n=40 n=50 LS 0.4034 0.2693 0.2107 0.1856 0.1571 0.0351 0.0215 0.0165 0.0136 0.0119 LA 0.5043 0.3212 0.2568 0.2314 0.1976 0.0424 0.0260 0.0203 0.0173 0.0151 Huber 0.4089 0.2715 0.2146 0.1880 0.1625 0.0353 0.0217 0.0167 0.0138 0.0121 GM 0.5338 0.3717 0.3087 0.2719 0.2257 0.0441 0.0287 0.0236 0.0206 0.0176

表2 离群值为情形2时，不同样本量下4种方法的和估计的平均绝对偏差Table 2 Mean absolute error of the estimators α^ and β^ based on the four methods under different sample sizes when the outlier is in case 2

表2 离群值为情形2时，不同样本量下4种方法的和估计的平均绝对偏差Table 2 Mean absolute error of the estimators α^ and β^ based on the four methods under different sample sizes when the outlier is in case 2

MAE(α^)MAE(images/BZ_6_1250_1625_1276_1679.png)n=10 n=20 n=30 n=40 n=50 n=10 n=20 n=30 n=40 n=50 LS 1.4159 0.7052 0.4834 0.3819 0.2911 0.1063 0.0489 0.0327 0.0233 0.0195 LA 0.5573 0.3488 0.2913 0.2244 0.1969 0.0513 0.0284 0.0214 0.0174 0.0142 Huber 0.5154 0.2957 0.2467 0.1964 0.1673 0.0477 0.0242 0.0181 0.0144 0.0121 GM 0.5280 0.3916 0.3272 0.2625 0.2420 0.0440 0.0292 0.0243 0.0202 0.0179

表3 离群值为情形3时，不同样本量下4种方法的和估计的平均绝对偏差Table 3 Mean absolute error of the estimators α^ and β^ based on the four methods under different sample sizes when the outlier is in case 3

表3 离群值为情形3时，不同样本量下4种方法的和估计的平均绝对偏差Table 3 Mean absolute error of the estimators α^ and β^ based on the four methods under different sample sizes when the outlier is in case 3

MAE(α^)MAE(images/BZ_6_1250_1625_1276_1679.png)n=10 n=20 n=30 n=40 n=50 n=10 n=20 n=30 n=40 n=50 LS 1.4242 0.6839 0.4556 0.3102 0.2629 0.1533 0.0677 0.0432 0.0294 0.0245 LA 0.7128 0.3637 0.2930 0.2264 0.2041 0.0713 0.0308 0.0224 0.0177 0.0153 Huber 0.6660 0.3298 0.2496 0.1982 0.1664 0.0709 0.0288 0.0197 0.0153 0.0126 GM 0.5726 0.3993 0.3315 0.2668 0.2364 0.0485 0.0304 0.0249 0.0206 0.0179

表4 离群值为情形4时，不同样本量下4种方法的和估计的平均绝对偏差Table 4 Mean absolute error of the estimators α^ and β^ based on the four methods under different sample sizes when the outlier is in case 4

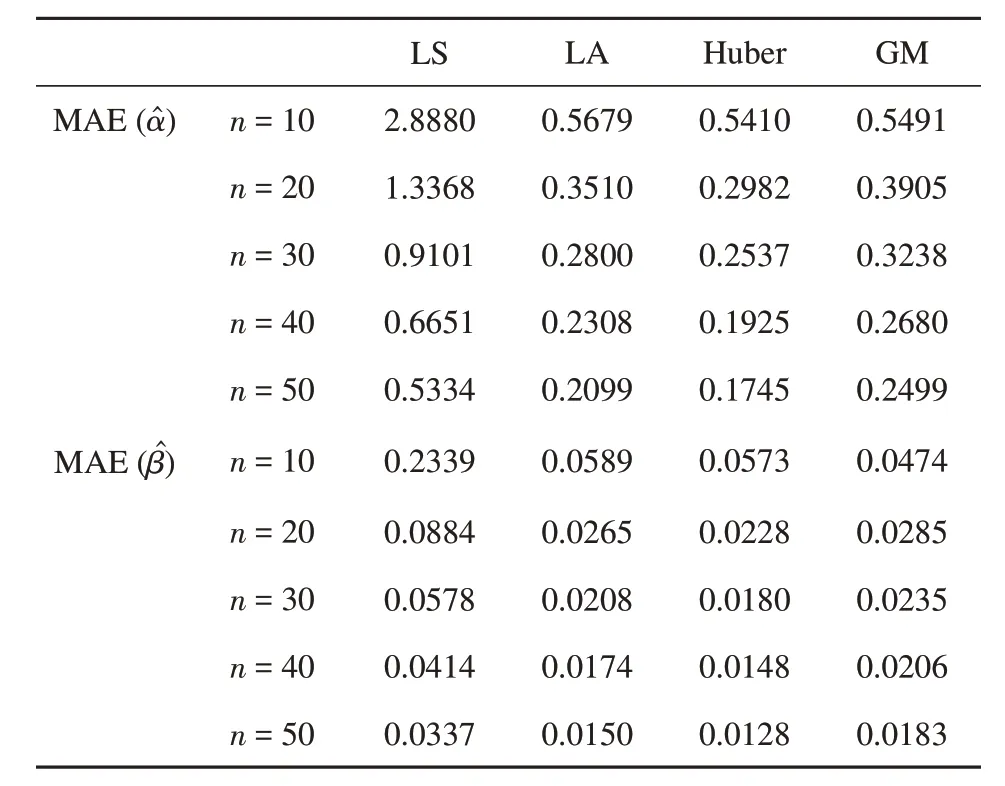
表4 离群值为情形4时，不同样本量下4种方法的和估计的平均绝对偏差Table 4 Mean absolute error of the estimators α^ and β^ based on the four methods under different sample sizes when the outlier is in case 4

MAE(α^)MAE(images/BZ_6_1250_1625_1276_1679.png)n=10 n=20 n=30 n=40 n=50 n=10 n=20 n=30 n=40 n=50 LS 2.8880 1.3368 0.9101 0.6651 0.5334 0.2339 0.0884 0.0578 0.0414 0.0337 LA 0.5679 0.3510 0.2800 0.2308 0.2099 0.0589 0.0265 0.0208 0.0174 0.0150 Huber 0.5410 0.2982 0.2537 0.1925 0.1745 0.0573 0.0228 0.0180 0.0148 0.0128 GM 0.5491 0.3905 0.3238 0.2680 0.2499 0.0474 0.0285 0.0235 0.0206 0.0183

从表1～4 可以看出，当不存在离群值（情形1）时，四种方法的MAE 差不多。几种方法的MAE 都随着样本量的增大而减小。但是当存在离群值时，稳健估计法的表现明显比最小二乘法好。在较小的样本量下，Huber 和GM 方法的表现都比较好。随着样本量的增加，Huber 方法的表现优于其他方法。当离群值的粗差加大，由10 变为20，最小二乘法的MAE 增加的幅度很大，但三种稳健估计法的MAE几乎没有变化。

综合以上结果，Huber方法在离群值情形下能够得到较好的估计结果，因此后文将使用Huber方法进行实证分析。

3 实证分析

3.1 数据来源和描述统计

这里我们分析6 只股票，包括上海证券市场的浦发银行（PFYH，600001），上海机场（SHJC，600009），包钢股份（BGGF，600010）以及深圳证券市场的平安银行（PAYH，000001），深科技（SKJ，000021），华联控股（HLKG，000036），使用综合A 股市场作为市场组合。股票的月收益率数据从CSMAR 数据库下载（https：//www.gtarsc.com），时间从2015-01 到2018-06，因此样本量是n=42。用活期存款利率0.3%作为无风险利率。转化为月度利率也就是rf=0.003/12。各支股票和市场组合的基本信息和描述统计如表5 所示。

表5 各支股票的基本信息和描述统计Table 5 Basic information and descriptive statistics of the 6 stocks

3.2 β 系数的估计与结果分析

用公式R(j)*i=R(j)i-rf和R(j)*M=R(j)M-rf分别计算股票的超额回报率和市场组合的超额回报率，其中R(j)M的数据使用综合A 股市场的回报率。然后用Huber 方法拟合（3）式的模型。图2 画出了R(j)*M（横轴）和R(j)*i（纵轴）的散点图以及得到的拟合直线。和的值列在表6 中。我们看到6 支股票的系数有显著的差异。总的来说，银行、钢铁、交通运输业的β系数相对较小，在证券市场线图上处于较左侧的位置（图3），而电子和房地产行业有较大的β系数，在证券市场线图上处于较右侧的位置（图3）。

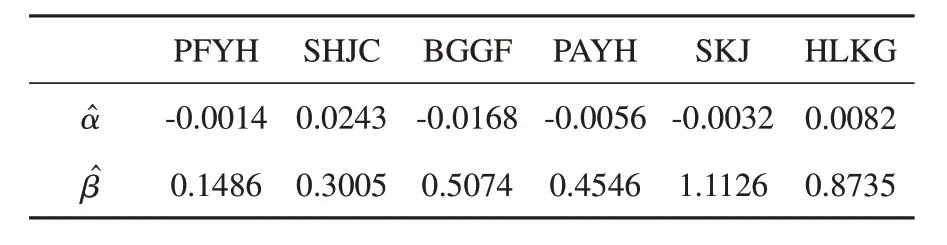
表6 6只股票Huber方法的α 和β 估计Table 6 The estimators of α and β for the 6 stocks based on the Huber method

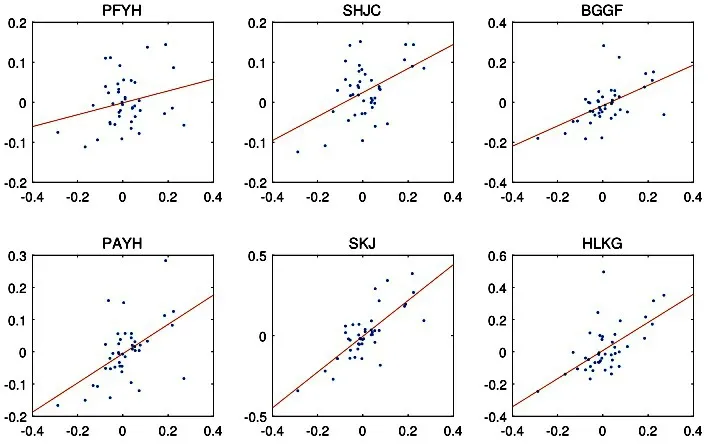
图2 市场组合的超额回报率和单只股票的超额回报率散点图以及基于Huber方法估计的回归直线Fig.2 Scatter plots of excess returns for market portfolio versus excess returns for individual stocks，and regression lines estimated based on theHuber method

图3 证券市场线和6支股票的相对位置Fig.3 The relative position of the security market line and the 6 stocks

4 总结

本文使用蒙特卡罗模拟来研究资本资产定价模型稳健估计量的表现，发现数据中有离群值时，最小二乘估计量会变得很不稳定，而稳健估计量仍然能够保持较小的误差。我们用这些方法来拟合CAPM 模型并分析了中国A 股市场2015 到2018 年几只股票的特征，发现不同行业风险系数的一些规律：银行、钢铁、交通运输业的β系数相对较小，而电子和房地产行业有较大的β系数。