考虑认知不确定性的热防护结构瞬态温度场分析

秦强 成竹

摘 要：瞬态温度场不确定性分析对高超声速飞行器热防护设计与评估有着重要的意义。本文考虑材料热物性参数的认知不确定性因素，提出了一种瞬态热传导温度响应的不确定性分析求解方法。首先，通过拉丁超立方抽样获得不确定性参数样本，将样本参数写入有限元计算文件中，用区间来表征参数的认知不确定性。其次，基于蒙特卡罗方法及有限元计算得到结构的不确定性瞬态温度响应曲线集。最后，以波纹夹芯热防护结构为例验证方法的可行性。研究结果表明，当结构有净热量流入时，由材料热物性参数的不确定性引起的瞬态温度响应的不确定性区间不断增大，并且瞬态温度响应的不确定性区间宽度与结构的温度变化具有正相关特点。

关键词：认知不确定性； 瞬态温度场； 有限元； 热防护； 拉丁超立方

中图分类号：V216.4 文献标识码：A DOI：10.19452/j.issn1007-5453.2023.05.008

高超声速导弹、高超声速飞机以及空天飞机等不同类别的高超声速飞行器在服役过程中都要遭遇严酷的气动加热环境 [1-3]。基于高超声速飞行器本体结构安全性极高要求，热防护结构（或热防护系统）成为高超声速飞行器的关键部件之一。热防护结构的作用是将进入飞行器内部的热量降到最低限度，使飞行器整体及其内部各部件在允许的温度范围内正常工作[4]。因此，相关科研工作者的研究重点一直集中在传热、强度分析、优化设计以及热防护结构的试验验证等方面。波纹夹芯结构主要由外面板、腹板、内面板三部分组成，是高超声速飞行器热防护结构中常用的被动式热防护结构[5-7]。热防护结构中常见的材料主要有陶瓷复合材料、高熔点的合金材料及碳碳复合材料等。

热传导分析是热防护结构设计的重要环节，目前在热传导研究方面，瞬态热传导问题吸引了众多学者[7-15]。在过去的瞬态热传导分析中，通常假设材料热物性参数、边界条件及初始条件等是确定的，继而可获得确定的瞬态温度场。但在实际工程中，尤其是高超声速飞行器热防护结构设计领域，许多结构的材料属性、载荷环境和几何尺寸存在误差和不确定性，致使不确定性建模与分析理论在传热领域得到越来越多学者和工程师的青睐[8-12]。近年来，国内外研究人员对热传导不确定性的问题进行了持续研究，取得了一些进展和成功，但仍存在利用概率方法有时结果不可靠、时域差分格式的复杂迭代、随着时间的推移而变化的分析结果以及容易产生较大误差等不足之处。

对于不确定性的表征和量化，主要有三种处理方法用于解决不同类型的不确定性问题，分别是随机模型、模糊模型和区间分析模型。区间分析模型适用于统计信息不足以描述不确定参数的概率分布或隶属函数，或只知道不确定参数的取值范围，想要得到响应的区间范围的情况。目前，考虑认知不确定性的区间表征方法在传热领域也引起了广泛的重视[13-17]。因此，本文针对工程热防护结构，以区间参数分析不确定温场问题，验证工程中区间不确定瞬态温场分析的可行性。

1 不确定性量化与传递

一般而言，确定性是相对的，而不确定性是绝对的，与之相对应的是几乎所有的设计变量和设计参数在实际工程设计中都存在某种不确定性。不确定性通常可分为随机不确定性和认知不确定性两大类，本文所研究的材料热物性参数不确定性属于随机不确定性的范畴。

不确定性可以用数学描述方法的不同来量化，基本可以分为两大类：一类是概率方法，另一类是非概率方法。概率法也可分为以频率为基础的经典概率法和理论上已经比较完善的贝叶斯概率论。正确描述不确定性的分布时所需要的样本信息比较大，这种方法一般只能用于处理随机不确定性，在实际工程领域被广泛接受和采用，用以描述不确定性的方法。目前主要有模糊集合理论、幅度分析、概率分界线解析等几种非概率的方法来应对不确定性[18-20]。本文中涉及的热防护材料由于研究数据较少，其热物性参数不具有一定的统计性规律，因此采用区间分析方法对參数不确定性进行量化。

在模型预测不确定性的量化中，不确定性的传递起着重要的作用，不确定性量化是定量描述和减少预测系统行为中不确定性的一种科学。目前，主要采用取样方法、扩展方法、快速建模方法和近似积分方法等来描述不确定性的正向传递。本文采用拉丁超立方这种最常用的方法来研究传递不确定因素。

在计算要求较高的模型计算中可以采用拉丁超立方抽样方法，其属于分层抽样的一种，优点就是高效，可以用相对较小的样本量提取大量不确定性信息[18]。

3 算例——波纹夹芯结构

波纹夹芯结构主要由外面板、腹板和内面板三部分组成，如图1所示。其是高超声速飞行器热防护系统中常用的被动热防护系统。

热防护系统常见的材料主要有高熔点的合金材料、陶瓷复合材料以及碳碳复合材料等。本文中波纹夹芯结构外面板和腹板使用材料相同，均为铝硅酸盐/ nextel 720纤维复合材料，内面板使用环氧树脂/碳纤维层压板。本文假设热防护系统外面板表面承受一定的热流载荷，内面板与周围环境发生热对流换热，而忽略隔热层内部的对流换热与热辐射，仅仅关注结构固体热传导过程。同时，为简化计算，假设材料的热物理属性与温度变化无关，设定为常数，并考虑由加工工艺等引起的材料热物性参数具有的不确定性。波纹夹芯结构的材料热物性参数及其不确定性区间见表1。

作为本次计算的气动热载荷，参考相关文献[6]中飞行器的热环境，并对其热流密度曲线做近似处理，如图2所示。波纹夹芯结构单胞的设计变量，参考国内外相关设计经验，如图3所示，其具体尺寸见表2。热分析有限元模型使用的是shell单元，共划分了660个单元、661个节点，如图4所示的波纹夹芯结构的有限元模型。

热边界采用热流密度热源，外面板上的热流密度曲线如图2所示，热流密度加载时间为2200s；内面板通常与飞行器舱内空气接触，承受舱内空气自然对流影响，因此假设内面板接触舱内空气侧的对流换热系数取10.0W/m2，环境温度和结构初始温度都取20℃。采用商用有限元软件瞬态热传导分析模块，求解波纹夹芯结构在0～6000s内的时域响应，时间步长设置为10s，得到了波纹夹芯结构在任意时刻下的温度分布情况，图5即为结构在5980s时的温度分布云图。从图5中可知，腹板上的温度梯度较大，结构整体隔热效果良好，外面板最大温度为798℃，而内面板整体温度均在100℃以下，实现了热防护的预期效果。

为了研究材料热物性参数的不确定性对结构瞬态温度场的影响，本文通过采用拉丁超立方抽样方法实现对不确定性的传递与量化。基于表1中所列的材料热物性参数不确定性区间，将每个参数的区间按相等的概率划分为1000份，生成互不重叠的子区间，在每个子区间不重复取样的情况下，进行随机等概率的取样。抽取1000组不确定性热物性参数样本，分别代入有限元模型文件中提交计算。分别选取腹板上下两端的节点A和节点B作为观测点，输出两节点的瞬态温度响应，不确定性有限元仿真结果分别如图6、图7所示。在图6与图7中，通过固定温度值所获得的温度范围，即为该节点在该时刻的瞬态温度响应的不确定性区间。表3与表4分别列出了节点A与节点B在1000s、2000s、3000s、4000s、5000s、6000s时刻下的瞬态温度响应不确定性区间及区间宽度值。

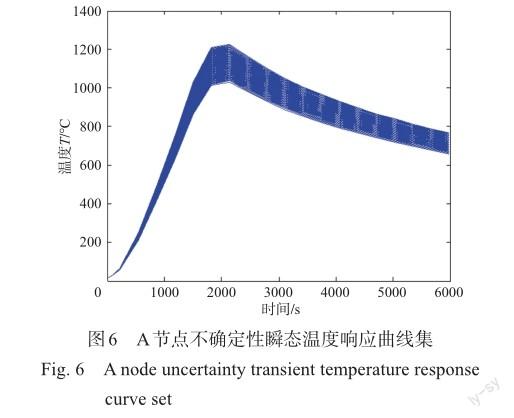
图6为腹板顶部A节点处的不确定性瞬态温度响应曲线集，从图6中可以看出，在0～2200s时间段内（外面板存在热量输入），随着时间的推移，节点A处温度迅速升高，与此同时，由材料热物性参数的不确定性引起的瞬态温度响应的不确定性区间也逐渐增大；在2200～6000s时间段内（外面板无热量输入），节点A处的温度缓缓降低，但此时，瞬态温度响应的不确定性区间，由于材料热物性参数的不确定而有微弱的变化。即热边界加载时，材料热物性参数的不确定性引起的瞬态温度响应的不确定性区间迅速增大；热边界卸载后，不确定性区间开始减小，但减小甚微。

图7为腹板底部B节点处的不确定性瞬态温度响应曲线集，从图7中可以看出，在0～2200s时间段内（外面板存在热量输入），随着时间的推移，B节点处温度缓慢升高，波纹夹芯结构热防护性能良好，B节点处温度低于40℃。与此同时，由材料热物性参数的不确定性引起的瞬态温度响应的不确定性区间也逐渐增大。在2200～6000s时间段内（外面板无热量输入），外面板及腹板的热量继续向内面板传递，节点B处的温度持续上升。同时，瞬态温度响应的不确定性范围继续增大，其原因是材料热物性参数的不确定性，在约4000s时（此时B节点处经腹板的热量流入与空气对流换热量相等）达到最大值，随后缓慢减小。即热边界加载时，材料热物性参数的不确定性引起的瞬态温度响应的不确定性区间逐渐增大；热边界卸载后，不确定性区间继续增大到一定值时才缓慢减小。

4 结论

材料熱物性参数、气动热载荷环境等的不确定性，使得高超声速飞行器结构瞬态温度响应不确定分析越来越受到重视。通过本文研究，主要得到以下结论：

（1）考虑材料热物性参数的认知不确定性因素，本文研究提出了一种瞬态热传导条件下的结构温度响应不确定性分析求解方法，即通过拉丁超立方抽样获得不确定性参数样本，并用区间表征参数认知不确定性，综合蒙特卡罗方法与有限元计算获取结构不确定性瞬态温度响应曲线集。

（2）利用本文提出的结构瞬态温度响应不确定性求解方法，以典型波纹夹芯结构为分析对象，计算了相应的不确定性瞬态温度响应曲线集，获取了材料热物性参数在不确定性区间条件下的瞬态温度响应不确定性特征：当结构有净热量流入时，由材料热物性参数不确定性引起的瞬态温度响应不确定性区间不断增大，且瞬态温度响应不确定性区间宽度与结构的温度变化呈正相关关系。

参考文献

[1]杨亚政，李松年，杨嘉陵. 高超音速飞行器及其关键技术简论[J]. 力学进展，2007，37（4）： 537-550. Yang Yazheng， Li Songnian， Yang Jialing. A review on hypersonic vehicles and key technologies[J]. Advances in Mechanics， 2007， 37（4）： 537-550. （in Chinese）

[2]陈召斌，廖孟豪，李飞，等.高超声速飞机总体气动布局设计特点分析[J].航空科学技术， 2022，33（2）： 6-11. Chen Zhaobin， Liao Menghao， Li Fei， et al. Analysis of design characteristics of overall aerodynamic layout of hypersonic aircraft[J]. Aeronautical Science & Technology， 2022， 33（2）： 6-11. （in Chinese）

[3]王小平，陈丽君，金行健，等.高超声速飞行器多源能量动态优化管理方法研究[J].航空科学技术，2022，33（8）： 9-15. Wang Xiaoping， Chen Lijun， Jin Xingjian， et al. Research on multi-source energy dynamic optimization management method of hypersonic aircraft[J]. Aeronautical Science & Technology， 2022， 33（8）： 9-15. （in Chinese）

[4]Myers D E， Martin C J， Blosser M L. Parametric weight comparison of advanced metallic， ceramic tile， and ceramic blanket thermal protection systems[R]. NASA /TM-2000-210289，2000.

[5]Lurie S A， Solyaev Y O， Volkov-Bogorodskiy D B， et al. Design of the corrugated-core sandwich panel for the arctic rescue vehicle[J]. Composite Structures， 2017， 160： 1007-1019.

[6]Zhang R， Zhang X， Lorenzini G， et al. Material combinations and parametric study of thermal and mechanical performance of pyramidal core sandwich panels used for hypersonic aircrafts[J]. Continuum Mechanics and Thermodynamics， 2016， 28（6）： 1905-1924.

[7]Ferraiuolo M， Manca O. Heat transfer in a multi-layered thermal protection system under aerodynamic heating[J]. International Journal of Thermal Sciences， 2012， 53： 56-70.

[8]Lamorte N， Friedmann P P， Glaz B， et al. Uncertainty propagation in hypersonic aerothermoelastic analysis[J]. Journal of Aircraft， 2014， 51（1）： 192-203.

[9]Lamorte N， Friedmann P P， Dalle D J， et al. Uncertainty propagation in integrated airframe-propulsion system analysis for hypersonic vehicles[J]. Journal of Propulsion and Power， 2014， 31（1）： 54-68.

[10]王琪，吉庭武，謝公南，等. 轻质热防护系统波纹夹芯结构热力耦合分析[J]. 应用数学和力学，2013，34（2）： 172-182. Wang Qi， Ji Tingwu， Xie Gongnan， et al. Structural analysis of corrugated-core sandwich panels for lightweight thermal protection system[J]. Applied Mathematics and Mechanics， 2013， 34（2）： 172-182. （in Chinese）

[11]Wang C， Qiu Z， Yang Y. Uncertainty propagation of heat conduction problem with multiple random inputs[J]. International Journal of Heat and Mass Transfer， 2016， 99： 95-101.

[12]张保强，陈国平，郭勤涛. 模型确认热传导挑战问题求解的贝叶斯方法[J]. 航空学报，2011， 32（7）： 1202-1209. Zhang Baoqiang， Chen Guoping， Guo Qintao. Solution of model validation thermal challenge problem using a Bayesian method[J]. Acta Aeronautica et Astronautica Sinica， 2011， 32（7）：1202-1209. （in Chinese）

[13]Majumdar S， Nayak S， Chakraverty S. Fuzzy and interval finite element method for heat conduction problem[J]. International Journal of Advances in Applied Sciences， 2012， 1（4）： 171-180.

[14]Wang C， Qiu Z， Yang Y. Collocation methods for uncertain heat convection-diffusion problem with interval input parameters[J]. International Journal of Thermal Sciences， 2016， 107： 230-236.

[15]杜秀云，唐祯安，薛齐文. 瞬态热传导温度场不确定性区间数值分析[J]. 功能材料，2013， 44（11）： 1558-1561. Du Xiuyun， Tang Zhen’an， Xue Qiwen. Uncertainty interval nu‐merical analysis of transient heat conduction temperature[J]. Jour‐nal of Functional Materials， 2013， 44（11）： 1558-1561. （in Chinese）

[16]李金平，陈建军，刘国梁，等. 具有区间参数的瞬态温度场数值分析[J]. 电子科技大学学报，2009，38（3）： 463-466. Li Jinping， Chen Jianjun， Liu Guoliang， et al. Numerical analysis of transient temperature field with interval parameters[J]. Journal of University of Electronic Science and Technology of China， 2009， 38（3）： 463-466. （in Chinese）

[17]薛燕妮，杨海天. 一个瞬态温度场区间上下界估计的数值方法[J]. 工程力学，2014 （9）： 7-13. Xue Yanni， Yang Haitian. A numerical method to estimate temperature intervals for transient heat transfer problems[J]. Engineering Mechanics， 2014 （9）： 7-13. （in Chinese）

[18]韩峰，杨万海，袁晓光. 基于模糊集合的证据理论信息融合方法[J]. 控制与决策，2010， 25（3）： 449-452. Han Feng， Yang Wanhai， Yuan Xiaoguang. Evidence theory information fusion method based on fuzzy set[J]. Control and Decision， 2010， 25（3）： 449-452. （in Chinese）

[19]肖無云，魏义祥，艾宪芸. 数字化多道脉冲幅度分析中的梯形成形算法[J]. 清华大学学报（自然科学版），2005（6）： 810-812. Xiao Wuyun， Wei Yixiang， Ai Xianyun. Trapezoidal shaping algorithm for digital multi-channel pulse height analysis[J]. Journal of Tsinghua University （Science and Technology）， 2005（6）： 810-812. （in Chinese）

[20]Helton J C， Johnson J D， Sallaberry C J， et al. Survey of sampling-based methods for uncertainty and sensitivity analysis[J]. Reliability Engineering & System Safety， 2006， 91（10-11）： 1175-1209.

Transient Temperature Field Analysis of Thermal Protectio1n Structure Considering Epistemic Uncertainty

Qin Qiang， Cheng Zhu

National Key Laboratory of Strength and Structural Integrity，Aircraft Strength Research Institute of China， Xi’an 710065， China

Abstract： The uncertainty analysis of transient temperature field is very important for the design and evaluation of hypersonic vehicle thermal protection. A transient thermal conduction analysis method for complex structure considering the thermophysical properties of materials with epistemic uncertainty is presented. The epistemic uncertainty parameter is characterized with interval and samples are obtained through Latin hypercube sampling. The structure of uncertainty transient thermal response curve set is obtained based on finite element analysis and Monte Carlo method and then the proposed method is validated by a corrugated core sandwich panel structure for uncertainty temperature field prediction. The results demonstrate that the uncertainty interval width of transient thermal response caused by material thermophysical parameter uncertainty increases continuously and it is positively correlated to the structure temperature changing when there is the net thermal flow into the structure.

Key Words： epistemic uncertainty； transient temperature field； finite element； thermal protection； Latin hypercube sampling