前飞状态旋翼变转速过程瞬态载荷过冲研究
宋彬 周云
摘 要:变转速旋翼在高速及长航时直升机等领域有巨大的应用前景,旋翼变转速过程的瞬态动力学响应及载荷特性,对直升机飞行控制和部件结构设计都至关重要。本文基于相对坐标描述的拉格朗日递推多体动力学方法,构建了一套旋翼变转速过程瞬态动力学分析模型,能够体现动态时变的旋翼转速和旋转角加速度对动力学响应的影响,在此基础上,对旋翼变转速过程的瞬态动力学行为进行了数值仿真分析研究。结果显示,旋翼变转速过渡过程,对摆振方向动力学影响十分显著,进而会引起旋翼轴扭矩瞬态载荷过冲现象;采用平滑进入/改成的变转速策略,有利于减小旋翼轴扭矩过冲载荷;旋翼升转速和降转速过程,会产生不同的动力学影响;变转速过渡时间是影响瞬态动力学特性最重要的因素,随着角加速度的增大,旋翼轴扭矩载荷过冲会急剧增大;旋翼拉力水平、前飞速度等飞行状态参数,主要影响稳定状态下的载荷基准值,对瞬态载荷过冲幅值也具有一定的影响。
关键词:变转速旋翼; 变转速过渡过程; 瞬态动力学; 多体动力学; 递推算法
中图分类号:V214.19 文献标识码:A DOI:10.19452/j.issn1007-5453.2023.05.003
高速、绿色、智能是未来直升机发展的主要方向,尤其高速直升机是目前各国研究和发展的重点。高速直升机为避免前行桨叶激波失速,在高速前飞状态必须降低旋翼转速,典型的XH-59A、X-2、X-3等高速直升机都采用了旋翼变转速技术[1-5]。另外,变转速旋翼技术还具有大幅降低直升机需用功率的潜力,美国波音公司基于最优转速旋翼技术(OSR)研制的A160无人直升机,续航时间达到20h,远远高于常规构型旋翼的无人直升机[6-7]。可以看到,变转速旋翼是发展高速和绿色长航时直升机必须突破的核心关键技术,有巨大的发展潜力和应用前景。但是,由于旋翼转速与直升机的气动升力、动力学特性、飞行控制等都密切相关,因此旋翼变转速会带来相当复杂的动力学问题[8-10]。
长期以来,为了规避旋翼变转速相关动力学问题,直升机一直都采用固定旋翼转速设计,直到近年来,随着高速及绿色直升机的兴起,研究人员开始关注变转速旋翼技术。R.W. Prouty[11]对变转速旋翼直升机的总体性能进行了研究,表明采用变转速设计可明显提高悬停升限、航时、航程和速度等性能指标。刘仕明等[12]则以某国产直升机为分析样例进行了转速优化策略研究,结果显示最大续航时间可以提升20.5%,最大航程可提高8.5%。马里兰大学Chopra教授团队在UMARC代码的基础上进行修改,建立了大前进比状态下的旋翼气弹分析模型,研究结果显示,根据飞行状态降低旋翼转速可大幅降低需用功率,但可能会导致桨叶载荷增大,指出并分析了大前进比旋翼拉力反向现象[13-15]。D.Anubhav 和 Y. Hyeonsoo等[16-17]基于全尺寸UH-60A 旋翼风洞试验,研究了大前进比状态下的动力学问题,发现了后行桨叶逆弦长方向动态失速现象和后行侧小拉杆存在脉冲载荷等现象。D. Han等[18-20]研究了变转速旋翼摆振动力学问题,并设计了桨叶嵌入式弦向吸振器,以降低摆振弯矩载荷。余智豪等[21]基于哈密顿(Hamilton)原理以及中等变形梁理论建立旋翼动力学方程,并针对大反流区气动力计算方法和大前进旋翼气弹配平计算方法进行修正,对大前进比状态下的桨叶载荷进行了研究。Xie Jiayi 等[22]采用自由尾迹模型,开展了变转速桨叶气动优化设计研究。文献[23]为研究舰载直升机起降过程桨叶挥舞响应问题,在中等变形梁模型基础上,推导了含Ω?相关惯性力项的显式桨叶动力学方程,但表达式相当复杂冗长。总的来讲,变转速旋翼相关研究尚处于起步阶段,目前的研究工作大多集中在旋翼降转速后,稳态大前进比条件下引起的气动及动力学现象与特性分析,对于变转速桨叶应该如何设计,还未形成统一的设计思路或设计准则,对旋翼变转速过程的瞬态动力学问题的研究还较少。
传统直升机旋翼其实也存在变转速过程,但它基本是在悬停且接近零升力状态变转速,因此旋翼载荷很小,对动力学的影响不显著。在高速前飞状态下,旋翼载荷较大,结构本身又有很大的转动惯量,且变转速旋翼必然存在转速切换的过渡过程,旋翼变转速过程的瞬态动力学响应及载荷特性,对直升机飞行控制和部件结构设计都至关重要。因此,本文根据旋翼系统具有典型树状拓扑结构的特点,基于拉格朗日多体动力学框架,建立一套旋翼变转速过程瞬态动力学分析模型,研究和揭示变转速过渡过程的旋翼瞬态动响应及载荷特性,为变转速直升机设计提供动力学理论基础。
1 计算方法与模型验证
1.1 变转速旋翼多体动力学模型
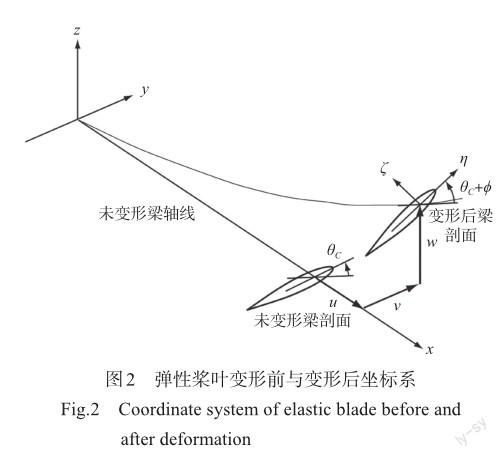
图1所示是典型旋翼系统示意图,它具有非常复杂的运动形式,首先是桨叶绕旋翼轴做大范围的旋转运动,其次是桨叶通过铰链与桨毂连接,有刚体挥舞、刚体摆振和刚体变距运动,最后是细长的桨叶,还有复杂的拉伸、挥舞、摆振和扭转弹性形变耦合運动。对于这种树状拓扑结构的动力学系统,基于多体动力学方法,采用拉格朗日相对坐标描述比较直观和方便,可以获得最小广义坐标数目的常微分动力学方程组,为此引入多个坐标系统进行旋翼系统运动学描述,各级坐标系之间的转换关系详见参考文献[24]。

进而可以得出由广义力形式表达的桨叶运动非线性微分方程


从式(7)可以看出,为计算系统动力学矩阵和矢量,需要计算桨叶上任意点位置矢量R的导数及偏导数相关项,根据旋翼系统树状拓扑构型特点,位置矢量R的导数及偏导数相关项可通过递推计算方式得到。



1.3 旋翼变转速过程瞬态气弹分析流程
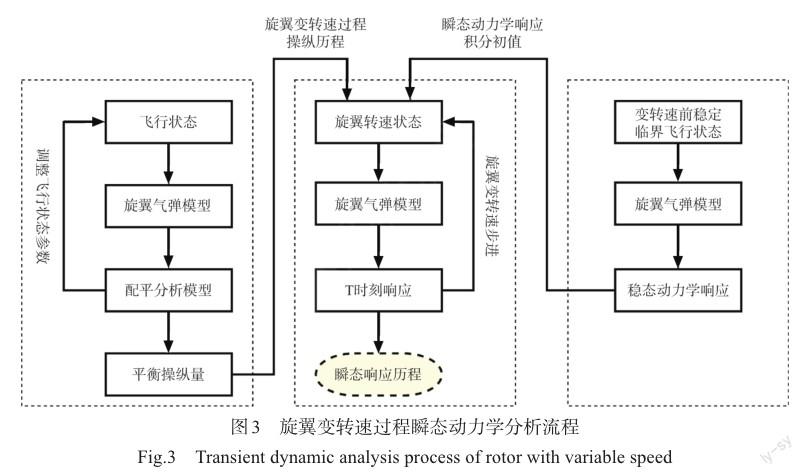
旋翼变转速过程,必然会引起直升机旋翼桨毂力和力矩的跟随变化,为了保持直升机平衡,必须同步进行总距和周期变距匹配操纵调整。因此,首先进行各种旋翼转速状态下配平计算分析,获得各旋翼转速状态下的配平操纵量,作为旋翼变转速过程瞬态动力学计算的操纵输入历程。接着在给定飞行状态下进行稳态气弹响应计算,收敛得到旋翼运动及变形的平衡位置。最后以此稳态动力学响应为积分处置,基于预定的旋翼转速和旋转角加速度变化历程,根据总距和周期变距操纵输入历程,进行瞬态动力学响应时程积分计算,直到达到目标旋翼转速,获得旋翼变转速过程的瞬态动力学响应及载荷。旋翼变转速过程瞬态动力学分析流程如图3所示。
1.4 模型验证
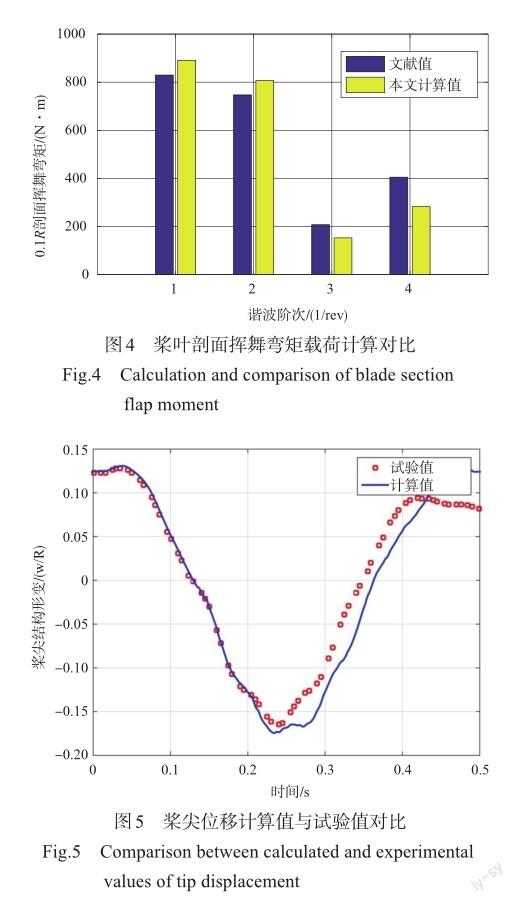
首先利用XH-59A旋翼参数进行模型验证,XH-59A桨叶详细结构特性参数见参考文献[27]。表1给出了XH-59A旋转桨叶固有频率本文计算值与文献值的对比,两者基本一致,验证了本文桨叶结构动力学模型的正确性,由于操纵线系刚度未提供相关参数,扭转方向频率未进行对比。图4给出了前进比为0.25状态下上旋翼桨叶0.1R剖面处挥舞弯矩前四阶谐波幅值计算对比情况,可以看出,本文计算的1/rev和2/rev桨叶动载荷较风洞试验值稍偏大,可能的原因是没有采用XH-59A旋翼桨叶所用翼型的气动数据,而是采用OA309翼型数据进行计算,但OA309翼型相较更优,总体来说,本文计算结果与文献试验值吻合程度较好,表明了本文计算方法的有效性。
进一步利用文献数据进行桨叶瞬态动力学响应计算验证,Keller采用与H-46纵列式直升机桨叶1/8弗罗德数相似的模型桨叶进行了桨叶扬起下坠试验,桨叶长1.006m,重0.998kg,质量和刚度分布见文献[28],初始状态时,桨叶根部固支,桨叶挥舞角为9.7°,在自重作用下桨叶有初始位移。突然释放根部挥舞铰约束,桨叶下坠,在挥舞限动角为0°时,桨叶与挥舞限动块碰撞,试验测试了桨尖位移随时间变化曲线,图5给出了桨尖位移计算值与试验值对比,由圖可以看出,计算与试验值吻合度较好,说明该计算模型可用于桨叶瞬态动响应计算。

2 数值仿真及分析
本文数值仿真分析基于一副变转速刚性旋翼,根据上述的旋翼变转速过程瞬态气弹分析流程,首先进行配平计算分析,获得变转速过程的操纵输入时域历程,以保证直升机在变转速过程中始终保持拉力恒定,表2所示是旋翼拉力T=2.5kN、变转速临界点前飞速度V=300km/h状态下的准静态配平操纵量。

2.1 变转速过程基本特性

图8~图10依次给出了桨根挥舞弯矩、桨根摆振弯矩和桨根扭矩载荷变化情况,可以看出,变转速过程对挥舞和扭转方向动力学影响较小,主要是从一个状态相对平稳地转移到另一个状态,瞬态效应不显著。对桨根摆振弯矩影响明显一些,一是随着旋翼转速降低,前进比增大,桨盘左右不对称性增大,导致桨叶动载荷变大。另外,变转速过程桨根摆振弯矩出现较多毛刺,经傅里叶变换(FFT)频谱分析,主要是一阶摆振模态频率成分,由于摆振模态的模态阻尼很小,旋转角加速度阶跃变化,很容易激励起摆振固有模态动力学响应。

图11和图12所示分别是旋翼轴扭矩载荷变化示意图和扭矩载荷频谱图,可以看出,变转速过程对旋翼轴扭矩的影响非常显著,在变转速开始和结束的瞬间,出现非常显著的瞬态旋翼轴扭矩载荷,对10~15s数据段进行FFT频谱分析,其主要频率为7.397Hz,对应的即是一阶摆振固有频率,根据旋翼动力学基本理论,旋翼桨毂具有滤波器特性,在稳态情况下,桨根摆振弯矩仅有静态成分和Nb /rev成分会传递给旋翼轴扭矩,其中Nb是旋翼桨叶片数,在变转速瞬态情况下,一阶摆振固有频率的非转速谐波成分也会传递给旋翼轴扭矩,即使单片桨叶的摆振弯矩变化不是很显著,但“集合”起来传递给旋翼轴后影响就会非常突出。

2.2 变转速策略分析
旋翼变转速是一个动态过程,旋翼从一个转速变化到另一个转速,总是需要经历一个加速和减速过程,图13和图14所示给出了两种变转速策略下的旋翼转速和旋转角加速度变化历程示意图,式(18)所示的是线性过渡策略,式(19)所示的是平滑过渡策略,可以看出,当采用旋翼转速线性过渡策略时,在转速变化临界时刻点,旋转角加速度会出现一个阶跃突变,采用平滑过渡策略时,旋转角加速度则变化平缓得多。
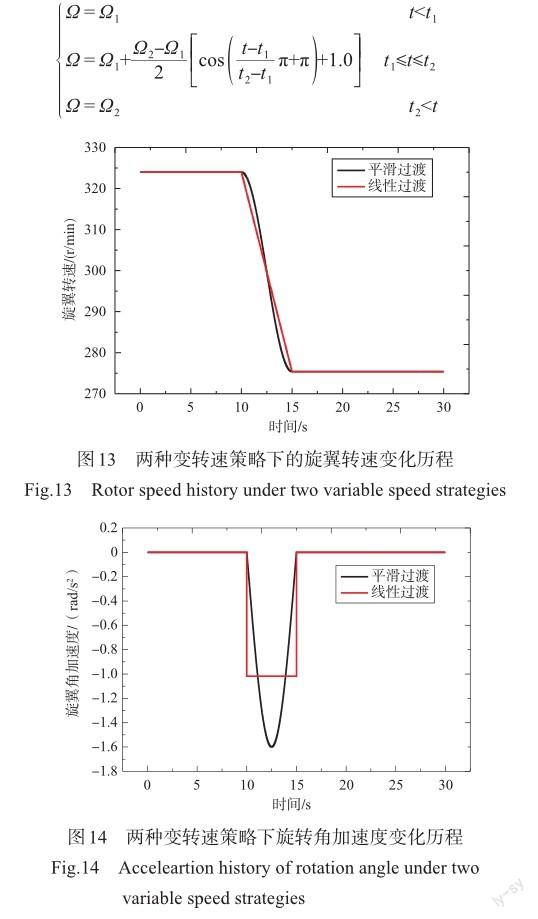
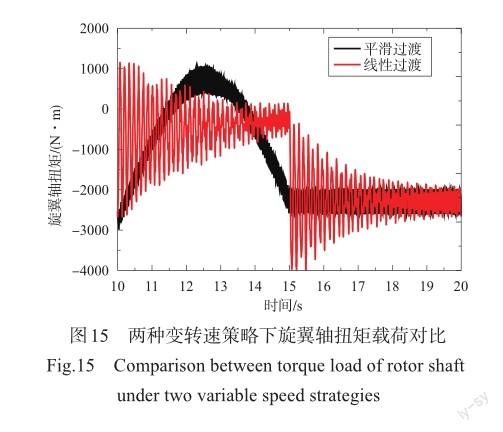
图15所示是线性变转速和平滑变转速两种策略下的旋翼轴扭矩载荷对比图,可以看出,线性变转速策略产生显著的瞬态动载荷,旋转角加速度的阶跃变化,相当于给动力学系统宽频激励,会激励起桨叶摆振固有频率动力学响应,进而将动载荷传递给旋翼轴扭矩,过大的瞬态扭矩可能对发动机的工作状态产生严重影响,过大的交变瞬态弯矩有可能造成动力和传动系统的损伤,平滑变转速策略更多地是出现旋翼轴静态扭矩载荷的变化。
2.3 变转速过渡时间分析
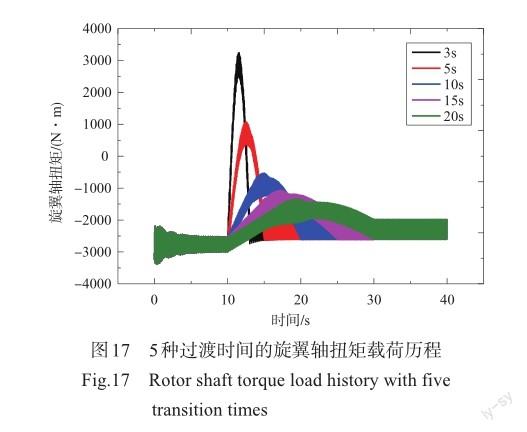
从上面分析可以看出,旋转角加速度对变转速过程的瞬态动力学行为有着极为重要的影响,变转速过渡时间的长短,直接决定了旋转角加速度的大小。采用式(19)所示的平滑进入和平滑改成的变转速策略,如图16所示,旋翼从100%转速降到85%转速,用时分别为3s、5s、10s、15s和20s共5种情况下的旋转角加速度变化历程,图17是5种过渡时间的旋翼轴扭矩载荷变化情况,可以看到,旋翼变转速过程会出现旋翼轴扭矩瞬态过冲的现象,随着过渡时间变短,旋转角加速度增大,从而带来瞬态过程惯性力增加,旋翼轴扭矩载荷过冲急剧增大,扭矩最大值出现在旋转角加速度最大的地方。旋翼降转速前稳定状态,旋翼轴扭矩值约为-2800N·m,当过渡时间小于5s时,旋翼轴扭矩变为正值,也就是出现旋翼轴扭矩值反向的现象,这本身在物理上是不可实现的。

2.4 降转速与升转速过程对比分析
图18所示是旋翼降转速过程和升转速过程的旋转角加速度变化情况,以及对应的动力学系统减速和加速过程,可以看到,降转速和升转速过程的旋转角加速度符号是相反的,对应的旋翼轴扭矩如图19所示。旋翼降转速过程类似于汽车减速过程,只要松油门,降低旋翼轴扭矩输出即可,但从图19的旋翼轴扭矩变化图可以看到,旋翼轴扭转从稳态时的负扭矩值,逐渐减至零,进一步过冲到一个正扭矩值,出现旋翼轴扭矩反向的情况,这种情况说明旋翼系统无法在这么短的时间内自己实现这一减速过程,必须使用旋翼刹车才可能降下来。旋翼升转速过程,旋翼轴扭矩值的符号始终与稳态时保持一致,最大的瞬态载荷过冲幅值达到稳态扭矩值的三倍,这个类似于汽车加速过程,需要发动机提供足够大的扭矩才能实现如此快的旋翼升转速过程。因此,旋翼降转速过程和升转速过程,基本是镜像对称的,但由于它的基准线不是零,故最终对动力学系统产生的影响和后果是截然不同的。
2.5 飛行状态的影响分析
图20给出了旋翼变转速临界点前飞速度对瞬态旋翼轴扭矩载荷的影响,计算分析了250km/h和300km/h两种前飞速度情况,可以看出,飞行速度越高,稳态时的旋翼轴扭矩动态值越大,相应的变转速过程的瞬态过冲也越大,250km/h对应的扭矩值约为-1475N·m,300km/h对应的扭矩值约为-1069N·m,说明在更小的前飞速度下进行旋翼变转速,有利于减小瞬态载荷冲击。图21给出了旋翼拉力状态对瞬态载荷的影响,计算分析旋翼拉力为2kN和2.5kN两种情况,可以看出,小的旋翼拉力状态,意味着更小的稳态扭矩载荷,同时瞬态过冲载荷也更小。总的来说,旋翼前飞速度及拉力水平等飞行状态,主要影响稳定状态下的载荷基准值,对瞬态过冲载荷具有一定的影响,但总体的影响不是很突出。


3 结论
本文基于相对坐标描述的拉格朗日多体动力学递推算法,建立了旋翼变转速过程瞬态动力学分析模型,开展了数值仿真分析研究,研究结论主要包括:
(1)旋翼变转速过渡过程主要影响旋翼摆振动力学,对挥舞和扭转影响较小;旋转桨叶摆振静态、N/rev谐波成分以及非谐波频率成分结构固有频率载荷,会传递到旋翼轴,形成旋翼轴扭矩瞬态载荷过冲现象,进而可能影响到传动系统、发动机等传动链部件。
(2)采用平滑进入和平滑改出的旋翼变转速策略,可以减小旋翼变转速对桨叶结构固有模态的阶跃激励响应,进而有利于减小瞬态载荷。
(3)变转速过渡时间即是旋翼旋转角加速度,是影响变转速过程瞬态载荷最重要和最敏感的因素,过渡时间减少,旋翼轴扭矩载荷过冲会急剧增大。
(4)旋翼降转速过程和升转速过程产生的动力学影响是截然不同的。降转速过程,旋翼轴扭矩产生反向的瞬态过冲载荷;升转速过程,旋翼轴扭矩产生同向的瞬态过冲载荷,此时需要发动机提供足够大的扭矩载荷。
(5)对于变转速临界点的前飞速度、旋翼拉力水平等飞行状态,主要影响稳定状态下的载荷基准值,对瞬态过冲载荷具有一定的影响,在较低的前飞速度和较小的旋翼拉力水平状态下进行变转速,有利于减小瞬态载荷。
本文从孤立旋翼的角度,基于预定的旋翼转速及旋转角加速度变化历程,对旋翼变转速过程的瞬态动力学响应及载荷进行了计算分析研究,综上所述,旋翼变转速过渡过程会对桨叶摆振、旋翼轴扭矩,进而对传动系统、发动机等传动链部件产生重要的动力学影响,下一步将建立变转速旋翼/传动/发动机耦合动力学模型,开展进一步研究。
参考文献
[1]邓景辉. 直升机技术发展与展望[J].航空科学技术,2021,32(1):10-16. Deng Jinghui. Development and prospect of helicopter technology[J]. Aeronautical Science&Technology, 2021, 32(1): 10-16.(in Chinese)
[2]吴希明,张广林,牟晓伟. 中国直升机产业的现状及发展建议[J].航空科学技术,2021,32(1):3-9. Wu Ximing, Zhang Guanglin, Mu Xiaowei. China helicopter industry status and development proposal[J]. Aeronautical Science & Technology,2021,32(1):3-9.(in Chinese)
[3]周云,胡和平,余智豪.高速升力偏置旋翼桨叶结构形变特性研究[J].航空科学技术,2021,32(6):57-64. Zhou Yun,Hu Heping,Yu Zhihao.Research on blade structure deformation characteristics of high-speed lift offset rotor[J]. Aeronautical Science & Technology, 2021, 32(6): 57-64. (in Chinese)
[4]Ashish B. Aerodynamic design of the X2 technology demonstratorTM main rotor blade[C].The 64th Annual Forum of the American Helicopter Society, 2008.
[5]Constantin O, Felix F, Jakob T, et al. Compound helicopter X-3 in high-speed flight: Correlation of simulation and flight test[C]. The Vertical Flight Society 75th Annual Forum & Technology Display, 2019.
[6]James D, David F. Operational benefits of an optimal, widely variable speed rotor[C].The American Helicopter Society 66th Annual Forum,2010.
[7]Blackwell R, Millott T. Dynamics design characteristics of the sikorsky X2 technologyTM demonstrator aircraft[C]. The American Helicopter Society 64th Annual Forum,2008.
[8]Graham B D, Inderjit C. Aeromechanics of a slowed rotor[C]. 56th AIAA/ASCE/AHS/ASC Structure, Structural Dynamics and Materials Conference, 2015.
[9]徐明. 最優转速旋翼直升机总体气动技术研究[D]. 南京:南京航空航天大学,2015. Xu Ming. Research on aerodynamic and preliminary design of helicopter with OSR [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015.(in Chinese)
[10]池骋,陈仁良. 旋翼转速变化对直升机需用功率、配平、振动及噪声的影响分析[J]. 南京航空航天大学学报,2018,50(5): 629-639. Chi Cheng, Chen Renliang. Influence of rotor speed variation on required power, trim, vibration and noise of helicopter[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2018, 50(5): 629-639. (in Chinese)
[11]Prouty R W. Should we consider variable rotor speed [J]. Vertiflite, 2004, 50(4): 24-27.
[12]刘士明,杨卫东,董凌华,等. 优化转速旋翼性能分析与应用[J]. 南京航空航天大学学报,2014,46(6):889-894. Liu Shiming, Yang Weidong, Dong Linghua, et al. Performance investigation and application of optimum speed rotors[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(6):889-894.(in Chinese)
[13]Graham M B. Performance and loads of variable tip speed rotorcraft at high advance ratios [D]. Maryland: University of Maryland, 2015.
[14]Benjamin B. Fundamental understanding of rotor aeromechanics at high advance ratio through wind tunnel testing [D]. Maryland: University of Maryland, 2016.
[15]Wang X, Andre B, Shashank M. Slowed hingeless rotor wind tunnel tests and validation at high advance ratios[C]//The Vertical Flight Society 75th Annual Forum & Technology Display, 2019.
[16]Anubhav D, Hyeonsoo Y, Thomas R N. Experimental investi‐gation and fundamental understanding of a slowed UH-60A ro‐tor at high advance ratio[C]. The American Helicopter Society 66th Annual Forum, 2011.
[17]Hyeonsoo Y. Investigation of performance and loads of a UH-60A rotor at high advance ratios[C].The American Helicopter Society 68th Annual Forum, 2012.
[18]Han D, Edward C S, Robert C B, et al. Comprehensive modeling and analysis of rotorcraft variable speed propulsion system with coupled engine/transmission/rotor dynamics[R]. NASA/CR-2013-216502, 2013.
[19]Han D, Edward C S. Lagwise resonance crossing analysis of a variable speed rotor[C].The 3rd International Basic Research Conference on Rotorcraft Technology, 2009.
[20]黃东盛,吴世杰,韩东. 变转速模型旋翼挥舞摆振低阶载荷试验研究[J]. 航空学报,2016, 37(3): 873-882. Huang Dongsheng, Wu Shijie, Han Dong. Experimental investigation of flapwise and lagwise lower harmonic loads of a variable speed model rotor[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 873-882.(in Chinese)
[21]余智豪,周云,宋彬. 大前进比变转速旋翼气弹动力学建模与载荷特性分析[J]. 振动与冲击,2021,40(4): 17-22. Yu Zhihao, Zhou Yun, Song Bin. Aeroelastic modeling and load analysis of a variable speed rotor in high advance ratio[J]. Journal of Vibration and Shock, 2021,40(4): 17-22.(in Chinese)
[22]Xie J Y, Xie Z F, Zhou M, et al. Multidisciplinary aerodynamic design of a rotor blade for an optimum rotor speed helicopter[J]. Applied Sciences, 2017,17(6): 89-97.
[23]Zheng Z C, Cheng Y M, Ren G X. Aeroelastic response analysis of a coupled rotor/fuselage helicopter system (I) modeling of the rotary-wing system[J]. Chinese Journal of Applied Mechanics, 1999, 16(1): 32-39.
[24]Anubhav D. Fundamental understanding, prediction and validation of rotor vibratory loads in steady level flight [D]. Maryland: University of Maryland, 2004.
[25]Wayne J. Comprehensive analytical model of rotorcraft aerodynamics and dynamics volume II : components theory[M]. California: Johnson Aeronautics, 2020.
[26]Felker F F. Performance and loads data from a wind tunnel test of a full-scale coaxial, hingeless rotor helicopter[R]. USAARAD‐COM-TR-81-A-27, 1981.
[27]Keller J A, Smith E C. Experiment/theoretical correlation of analysis for helicopter rotor blade/droop stop impacts[J]. Journal of Aircraft, 1999,36(2):443-451.
Transient Load Overshoot of Rotor During Varying Speed Process in Forward Flight
Song Bin, Zhou Yun
China Helicopter Research and Development Institute, Jingdezhen 333001, China
Abstract: Variable speed rotor has great application prospects in the fields of high-speed helicopter and long endurance helicopter. The transient dynamic response and load characteristics of rotor during varying speed process are very important for helicopter flight control and component structure design. In this paper, a lagrangian recursive multibody dynamics method based on relative coordinate description is presented, and constructs a set of transient dynamics model of rotor during varying speed process, which can reflect the influence of time-varying rotor speed and rotational angular acceleration on rotor dynamics. Based on this, the transient dynamic behavior of rotor is numerically simulated and analyzed. The results show that the transient process of rotor varying speed has significant impact on the rotor lag dynamics, which will cause rotor shaft torque overshoot. The variable speed strategy of smooth start and end is helpful to reduce transient loads. Rotor acceleration and deceleration process will cause different dynamic effects. The transition time is the most important factor affecting the transient dynamic characteristics. With the increase of angular acceleration, the over-shoot of rotor shaft torque will increase sharply. The flight conditions such as rotor thrust and forward flight speed mainly affect the load reference value in the steady state and have a certain influence on the overshoot amplitude of the transient load.
Key Words: variable speed rotor; varying speed transition process; transient dynamics; multibody dynamics; recursive algorithm

