基于ASTG-CRNN模型的多步长交通流预测

贵向泉,熊家昌,李 立,郭莎莎

(1.兰州理工大学 计算机与通信学院,甘肃 兰州 730050;2.中国石油天然气股份有限公司长庆油田分公司 数字化与信息中心,陕西 西安 710000)

0 引 言

随着城市化水平不断提升,大量人口涌向城市,城市中的出行车辆增多,导致城市居民所面临的交通拥堵问题日益突出。通过交通流预测,实现对未来交通状况的预测评估,进而完成车辆调度分流、拥堵风险评估等工作,这对于缓解城市交通压力具有重要作用。

文中研究的交通流特指交通流量,是在特定时间段内通过道路上某一断面的车流数。交通流量是量化交通通行能力的一种有效指标,准确的交通流预测信息可以为交通管理者提供有力的交通决策依据。目前交通流预测方法主要有两类:模型驱动方法和数据驱动方法。模型驱动方法根据数学理论假设预先确定模型,并用少量数据去拟合模型来实现交通流预测。这种方法存在模型结构单一、假设情况与现实情况较大差距等问题,导致预测模型在实际应用中预测效果不好。常用的预测模型有卡尔曼滤波模型[1]、自回归整合移动平均模型(ARIMA)[2]等。与模型驱动方法不同,数据驱动方法可以很好地克服交通流数据的不确定性。数据驱动方法分为传统机器学习方法和基于深度学习的方法。传统机器学习方法中被应用于交通流预测的模型有支持向量机回归(SVR)[3]、贝叶斯模型[4]、K最近邻(KNN)[5]等。尽管传统机器学习方法与模型驱动方法相比可以从交通流数据中学习统计规律,但其处理高维的交通流数据能力有限。

随着深度学习方法的兴起,具有高维数据处理和非线性数据特征挖掘能力的深度神经网络模型受到越来越多的青睐。Wang等人[6]提出一种长短记忆网络(LSTM)编码器-解码器结构的交通流预测模型,该模型能够准确地学习局部特征和长期依赖关系。Chen等人[7]构建了一种卷积LSTM模型来估计短期交通流,该模型能同时挖掘交通流数据中的时空特征。袁华等人[8]在卷积神经网络(CNN)的基础上提出扩张-因果卷积神经网络,分别用扩张卷积和因果卷积来增加感受野的大小和解决信息泄露问题。桂智明等人[9]利用卷积神经网络和门控循环单元(GRU)来提取交通流的时空特征,同时利用交通流的周相似性提取周期特征。凤少伟等人[10]提出一种K-means与GRU神经网络结合的交通流预测方法,该方法能够很好地挖掘交通流时间序列的关联性。传统的CNN、LSTM、GRU等模型能够很好地处理不平稳非线性序列问题,但其大多只能提取到交通流数据的局部信息,且无法应用于标准的网格数据中,而利用图卷积可以将神经网络应用于图结构的数据中。Lv等人[11]提出了一种时间多图卷积网络,用于联合建模道路网络中与各种全局特征的空间、时间、语义相关性。谷振宇等人[12]提出了一种基于时空图卷积循环神经网络的交通流预测模型,采用图卷积神经网络捕获交通流数据中的空间依赖关系,采用门控循环神经网络捕获交通流数据中的时空依赖关系。然而交通流数据在时空维度上不仅具有依赖性,也存在着较强的相关性,且相关性是动态变化的。为了对交通流数据中的动态相关性进行建模,Guo等人[13]提出了一种新的基于注意力机制的图卷积门控循环神经网络模型(ASTGCN),该模型使用利用图卷积网络捕获用于建模空间依赖的拓扑特征,同时利用注意力机制根据速度数据的重要程度为特征分配权重,进一步提高了模型的预测精度。Song等人[14]提出了一种时空同步图卷积网络模型(STSGCN),该模型通过精心设计的时空同步建模机制,能够有效地解决复杂的局部时空相关性以及局部时空图中的异质性问题。

车辆在道路网络系统上聚集成为交通流,交通流的产生、扩展以及状况演变过程与路网表征结构密切相关,因此路网表征结构的关系权重确定是影响道路交通流预测精度的主要因素。目前在路网表征结构的关系权重设计研究工作方面,一般采用单纯的逻辑关联(0或1)或以距离为运算准则的高斯核来表示,相连关系则表示为无向连接的,这种权重和连通关系的设计存在对路网的空间结构刻画能力不足的问题。同时,交通系统具有时空强耦合的特性,不同地点的交通状况相互影响,不同时间切片内的交通状况之间存在时间相关性,现有的交通流预测方法大多缺乏对交通流数据中的动态时空相关性进行建模的能力。并且现有研究在交通流数据中时间依赖性的挖掘上往往采用的是单一结构的模块,这存在对交通流数据中的时间特性挖掘不充分的问题。

针对上述问题,该文的研究工作情况如下:

(1)构建一种权重邻接矩阵,用节点的有向带权连通关系来刻画路网结构的有向性,通过定义节点相对邻近度来确定路网表征结构的关系权重,解决了对路网空间结构刻画不足的问题。

(2)在时空维度上引入注意力机制,自适应地赋予数据不同的重要性和捕获节点之间的动态相关性,解决了交通流数据中动态时空相关性难以进行建模的问题。

(3)采用卷积神经网络和双向门控循环神经单元的组合模块对已经提取过空间特征的交通流数据进行时间特征的捕捉,解决了对交通流数据中时间特性挖掘不充分的问题。

1 ASTG-CRNN模型

1.1 交通路网时空图构建

文中t时刻有向空间图Gt表述如式(1)所示。

(1)

其中,V是图Gt中检测节点(即为路网结构中的传感器)vi的集合,E表示图Gt中有向边的集合,(vi,vj)表示从节点vi到节点vj的交通流向,且(vi,vj)≠(vj,vi);A为权重连接矩阵,Aij表示节点vi与节点vj间的相对邻近度,如式(2)～式(4)所示。

(2)

(3)

(4)

其中,k(i)表示当dist(vi,vj)≤γ时,节点vi的k个邻域节点的集合,dist(vi,vj)为节点vi到vj的欧氏距离,γ为设置的阈值,当两个节点的距离超出阈值γ的大小,则代表两节点的权重系数为0,无依赖性。通过式(2)和式(3)可知,两节点的相对邻近度与如下因素有关:(1)两节点的欧氏距离;(2)整个路网图中的检测节点集合;(3)两节点的局部邻域节点。

1.2 模型设计

针对交通流的特点,提出一种基于注意力机制和时空图卷积循环神经网络的交通流预测模型(ASTG-CRNN),将交通路网中的部分路段作为检测路段来进行交通流预测。图1给出了ASTG-CRNN模型的总体框架。根据人们的日常生活规律,交通流数据会存在一定的周期性和规律性变化。因此,模型采用三个具有相同结构的独立组件,分别对历史交通流数据中的最近周期依赖关系、日周期依赖关系和周周期依赖关系进行建模,以便获取到交通流数据中更深度的周期性信息。

假设采样频率每天为q次,当前为t0时刻且预测序列段的长度为Tp。如图2所示,沿时间轴截取三个长度为Th、Td和Tw的时间序列片段,分别作为最近周期、日周期、周周期组件的输入,其中Th、Td和Tw均为Tp的整数倍,三个时间序列片段的具体情况如式(5)～式(7)所示:

图2 三个时间序列片段的构建示例

(1)最近周期时间序列片段,如图2中①所示,此序列段与要预测的时间序列段在时间维度上直接相邻。由于在现实生活中,交通拥堵的形成和分散是渐进的,因此与之直接相邻的历史时间序列会对其有较大影响。

Xh=(Xt0-Th+1,Xt0-Th+2,…,Xt0)

(5)

(2)日周期时间序列片段,如图2中②所示,此序列段由相邻几天中与要预测的序列段时间相同的序列段组成。由于人们在工作日的活动情况几乎是没有太大变化的,比如公司和家庭两点一线,存在固定的生活模式,因此交通流数据可能会呈现出重复的日周期模式。日周期组件的目的就是用来在时间维度上建模交通流数据中的日周期依赖性。

(3)周周期时间序列片段,如图2中③所示,此序列段是由相邻几周中与要预测的序列段时间相同的序列段组成。通常来说,当前周的工作日的交通流状况与历史周的工作日流量状况存在相似性,但是与历史周的周末的交通流状况存在不同。周周期组件是用来在时间维度上捕获交通流数据中的周周期性时间变化趋势。

Xt0-7*q+1,…,Xt0-7*q+Tp)

(7)

这三个组件具有相同的网络结构,每个组件由若干个时空模块组成。每个时空模块包含时空注意力模块、图卷积模块、卷积神经网络与双向门控循环神经单元的组合模块以及全连接层模块。最后,根据权重矩阵对三个分量进行融合,得到最终的预测结果。

1.3 时空注意力模块

(1)时间注意力模块。在时间维度上,不同时间切片上的交通状况之间存在相互关系,且相互关系在不同情况下也存在差异。使用一种注意力机制来自适应地赋予数据不同的重要性。以最近周期组件中的在第r层上时间注意力模块为例,如式(8)～式(9)所示:

(8)

(9)

(10)

(2)空间注意力模块。在空间维度上,不同区域内的交通状况存在一种相互的影响,且这种影响实际上还存在相当高度的动态性。用注意力机制来自适应地捕获在空间维度上节点之间的动态相关性。同样地,以最近周期组件第r层上的空间注意力模块为例,如式(11)～式(12)所示:

(11)

(12)

其中,Vs、bs、W1、W2、W3都为权重矩阵,σ被用作激活函数。Sij的值在语义上表示的是节点vi和节点vj之间的相关强度,Sj表示第j列中的所有元素。同样地,还需要对S进行归一化操作得到矩阵S'。

1.4 图卷积模块

在谱图分析中,一个图用它对应的拉普拉斯矩阵表示。图结构的性质可以从对应的拉普拉斯矩阵中分析获得。图的拉普拉斯矩阵可以定义为L=D-A,A为带权重的邻接矩阵,D为包含节点度的对角矩阵,拉普拉斯矩阵的特征分解如式(13)～式(14)所示:

L=UΛUT

(13)

Λ=diag([λ0,λ1,…,λN-1])

(14)

然而,当图的尺度变大时,对拉普拉斯矩阵进行特征值分解所付出的代价也随之变高。该文采用切比雪夫多项式来解决该问题,如式(15)～式(16)所示:

(15)

(16)

其中,参数θ为多项式系数的向量,λmax为拉普拉斯矩阵的最大特征值,⊙为哈达玛积。切比雪夫多项式的递归定义如式(17)所示:

Tk(x)=2xTk-1(x)-Tk-2(x)

(17)

且T0(x)=1,T1(x)=x,通过卷积核gθ提取图中每个节点周围0到K-1阶邻域的信息。

1.5 CNN-BiGRU组合模块

该文使用卷积神经网络(CNN)与双向门控循环神经单元(BiGRU)的组合模块对已经提取空间依赖关系的交通流数据再进行时间依赖关系的提取。通过合并相邻时间片上的信息来进一步堆叠时间维度上的卷积层,同样地,以最近周期时间组件在第r层的卷积操作为例,如式(18)所示:

(18)

使用ReLU作为组合模块中的激活函数,相较于SELU(缩放指数线性单元)具有更好的收敛性并且可以有效地避免梯度消失的问题。在进行完卷积操作后,还需要将结果输入到BiGRU中,用来增强对交通流数据中的时间依赖关系的提取。如图3所示,为了防止过拟合和提高运行效率,在卷积层之后添加了池化层。

BiGRU是由向前和向后两个单向的GRU层堆叠而成,其中前向GRU是对输入从开始到结束的前向交通流序列进行预测,后向GRU是对输入从结束到开始的反向交通流序列进行预测。由于综合考虑了前后时刻交通流对当前时刻交通流的影响,模型的精度得到了提升。以最近周期时间组件在第r层上BiGRU的输出为例,如式(19)所示:

(19)

(20)

最后还要将处理后的数据输入到全连接层模块,以确保当前时间组件下每个时空模块的输出具有相同的尺寸和形状。将多个时空模块进行叠加,可以进一步提取到更大范围的动态时空相关性。

1.6 多组件融合

当融合不同组件的输出时,三个组件的影响权重是不同的,并且影响权重可以从历史的交通流数据中学习到。融合后的最终预测结果如式(21)所示:

(21)

其中,Wh、Wd、Ww为权重矩阵,分别反映了三个时间维度组件对预测目标的影响程度。

2 实验设计

2.1 数据集描述

为了验证模型的有效性,选取美国公路的两个公开交通流数据集PeMS04和PeMS08进行实验验证。这些数据集是由Caltrans Performance Measurement System(PeMS)每30秒实时收集一次,并且交通流数据每隔5分钟汇总一次。PeMS04包含16 992条交通流数据以及采集这些信息的307个检测节点的地理位置信息;PeMS08包含17 856条交通流数据以及采集这些信息的170个检测节点的地理位置信息。

2.2 对比基线模型

为了对比分析预测模型的预测效果,选择在交通流预测中比较有代表性的预测模型,包括LSTM[15]、GRU[16]、ConvLSTM[17]、ASTGCN[13]以及STSGCN[14]作为对比基线模型。这些基线模型是参考对应文献进行构建。

2.3 评价指标设计

选取平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)作为实验验证评价指标。指标算法如式(22)～式(24)所示:

(1)平均绝对误差。

(22)

(2)均方根误差。

(23)

(3)平均绝对百分比误差。

(24)

2.4 模型参数

以6∶2∶2的比例将数据集划分为训练集、验证集和测试集。考虑到计算效率和预测性能的提升,设置切比雪夫多项式的项数为3。在训练阶段将MAE作为损失函数并进行重复实验对超参数进行调整,最后设置学习率为0.000 1,批量大小为64,训练迭代次数在PeMS04和PeMS08数据集上分别为200和80。

对于三个时间组件的长度,设置不同的Th、Td以及Tw值来比较模型的预测效果,如图4所示。从图4中可以看出,当Th=36、Td=24和Tw=24时,模型的预测效果较佳。同时设置预测窗口Tp=12,即目标是预测在未来一小时内的交通流。

图4 在PeMS04数据集上ASTG-CRNN模型置不同的Th、Td以及Tw值时在未来1h上预测结果的MAE对比

2.5 实验结果与分析

(1)各模型多步长预测结果。

用ASTG-CRNN模型和前述的5种基线模型分别对未来1h内的交通流进行预测,每5分钟为一步长,预测步长12步。在数据集PeMS04上ASTG-CRNN模型在前3步的预测效果优势不明显,如图5(a)(b)所示,MAE、RMSE要略差于STSGCN模型,而在后9步ASTG-CRNN模型的预测效果要优于其它基线模型,尤其是在MAPE指标上优势明显,如图5(c)所示。而在数据集PeMS08上ASTG-CRNN模型在前12步的预测效果均要优于其它基线模型,如图6(a)(b)以及(c)所示,尤其是在后6步上当STSGCN、ASTGCN的三项指标大幅降低的时候,ASTG-CRNN模型的三项指标降幅并不明显且指标数值低于其它基线模型,显示出该文提出的模型在多步长交通流预测方面有着一定的优越性。但在两项数据集上ASTG-CRNN等模型在三项评价指标上的抖动幅度要明显大于LSTM、GRU以及CNN-LSTM模型,这是因为LSTM、GRU以及CNN-LSTM模型只对交通流序列的时间或空间特征进行提取,而ASTG-CRNN等模型要同时考虑到时空相关性,对交通流序列的时间和空间特征进行捕捉,因而在稳定性方面ASTG-CRNN模型的效果要差些。ASTG-CRNN模型相较于其它基线模型的具体预测误差数值对比如表1所示。

表1 在未来15 min、30 min和1 h上ASTG-CRNN模型和基线模型的预测误差数值

图5 各模型在PeMS04数据集上不同时间步长的预测结果对比

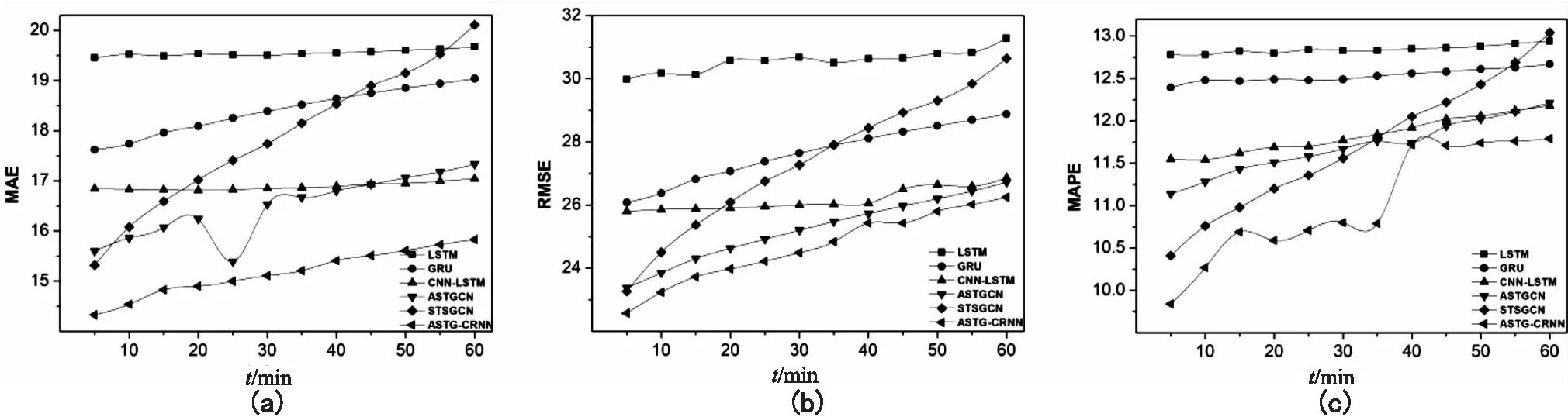
图6 各模型在PeMS08数据集上不同时间步长的预测结果对比

(2)各模型交通流预测值与真实值对比。

为了能直观地说明ASTG-CRNN模型的预测效果,分别在PeMS04和PeMS08数据集上随机选取一个路段,分别命名为路段1和路段2,并对这两个路段提前一小时的交通流预测情况进行可视化,对比各模型的预测值与真实值之间的误差,时间间隔为5分钟,如图7、图8所示。从图中可以看出,ASTG-CRNN模型对真实值的拟合效果最好,而其它模型存在明显的滞后性,尤其在时间段9:00-10:00上对比效果明显。这说明ASTG-CRNN模型能够有效预测出未来的交通流情况和趋势。

图7 各模型在PeMS04数据集上路段1的预测值与真实值对比

图8 各模型在PeMS08数据集上路段2的预测值与真实值对比

(3)消融实验。

为了凸显该文使用的注意力机制、CNN-BiGRU组合模型以及构建的有向带权邻接矩阵的优势,设置了对比实验分别验证其对模型的影响。STG-CRNN为ASTG-CRNN模型去除注意力机制后的模型,ASTG-RNN、ASTG-CNN分别为ASTG-CRNN模型去除CNN、BiGRU后的模型,NMASTG-CRNN模型为在ASTG-CRNN模型的基础上将邻接矩阵相连节点的权重设置为0或1后的模型。各模型在两种数据集上不同时间步长的RMSE预测结果如表2所示。由表1、表2可知,注意力机制对ASTG-CRNN模型的预测效果都有一定作用。ASTG-CRNN的效果要好于STG-CRNN,这是因为时空注意力机制可以对交通流数据中的时空相关性进行建模;ASTG-RNN、ASTG-CNN的预测效果比ASTG-CRNN差,这是因为CNN-BiGRU组合模型可以对交通流数据中的时间特征进行充分捕捉,从而捕获到隐藏的信息;而ASTG-CRNN相较于NMASTG-CRNN有着更低的预测误差,则说明通过构建权重邻接矩阵挖掘路网表征结构关系,比以简单的逻辑关系结构设计权重能够更好地表征路网结构。

表2 对比模型在不同时间步长上的RSME预测数值

3 结束语

提出的ASTG-CRNN交通流预测模型能够对路网表征结构进行准确刻画,解决交通流数据中动态时空相关性难以进行建模以及时间特征捕获不充分的问题。该模型首先定义检测节点相对邻近度对路网表征结构进行刻画,再引入时空注意力机制对交通流数据中动态时空相关性进行建模,随后再利用图卷积对交通流数据中的空间特征进行捕捉,最后利用CNN-BiGRU组合模块对交通流数据中时间特征进行充分捕捉。实验结果表明,ASTG-CRNN模型可以有效降低多步长交通流预测误差。