水平井压裂过程中水泥环界面窜流模拟分析

陈祝兴 李托 付海峰 翁定为 马泽元 李军，3

(1.中国石油勘探开发研究院 2.中国石油大学(北京) 3.中国石油大学(北京)克拉玛依校区)

0 引 言

页岩气储层具有低孔隙度和低渗透率的特点[1]，而常规开采方法无法满足天然气的商业生产需求。水平井多级压裂作为一种能显著提高低孔、低渗致密砂岩油气藏产量的储层改造措施[2]，已经广泛应用于页岩气的生产中。在水平井多级压裂的过程中，必须要保证各个压裂段间不发生窜流，从而增强压裂效果[3]。然而由于压裂施工的影响，套管内流体压力和温度的周期性变化可能导致水泥环密封失效，并在套管-水泥或水泥-地层界面产生微环隙[4]，压裂液通过微环隙侵入水泥环界面，导致压裂段间产生窜流，从而减弱压裂改造效果，甚至发生压裂失效。

K.E.GRAY等[5]通过将套管-水泥环界面建模作为接触条件，开发了数值模型来研究水泥环界面的脱黏，该方法允许界面上存在零张力或一定量的张力传递，分别对应无黏结强度和有限黏结强度的情况。B.LECAMPION等[6]通过室内试验得到了水泥环界面裂缝扩展的几何形状。WANG W.等[7]基于内聚力理论，建立了一个嵌入黏结带的耦合三维多孔弹性模型，分析了水力压裂过程中页岩地层和水泥环水力裂缝的扩展情况。FENG Y.及FENG Y.C.等[8-9]基于垂直井段，建立了一个三维有限元模型来模拟水泥环界面处的脱黏扩展，从而将界面脱黏的长度、宽度以及周向覆盖范围进行量化。赵效锋等[10]针对油气井生产过程中固井界面微环隙的产生和发展规律进行仿真试验研究，并对套管-水泥环界面的黏结力进行测量，建立了固井界面微环隙的理论计算方法。彪仿俊等[11]使用ABAQUS软件，采用三维流固耦合实体单元和Cohesive黏结单元描述岩石和裂缝的行为。

从上述研究可以看出，前人的研究主要针对水泥环微环隙的产生、水泥环界面的脱黏情况，并未定量分析水平井分段压裂过程中压裂液侵入水泥环界面的窜流长度，此外，也未考虑压裂液流速等因素对界面脱黏的影响。为此，本文利用ABAQUS软件，基于Cohesive单元方法，建立了水泥环界面窜流三维有限元模型，模拟压裂液侵入水泥环界面造成的窜流现象，对比水泥环-地层界面和水泥环-套管界面发生窜流的难易程度，研究水泥环弹性模量、泊松比及压裂液流速等因素对窜流长度的影响，并结合油田实例进行分析，以期为现场施工提供参考。

1 数学物理模型

以水泥环-地层界面为例，水泥环-套管界面原理与之相同。为了模拟流体驱动的界面脱黏，需要考虑2个关键因素：①多孔介质的变形和孔隙流体流动；②脱黏裂缝的扩展和裂缝内流体的流动。

1.1 水泥环-地层界面间流体的流动方程

水泥环和地层之间设置一个Cohesive单元，该Cohesive单元即表示水泥环-地层的界面性质。压裂液则沿着水泥环-地层界面的Cohesive单元进行法向流动和切向流动。法向流动的方向垂直于Cohesive单元所在的平面，切向流动的方向平行于Cohesive单元所在的平面，如图1所示。

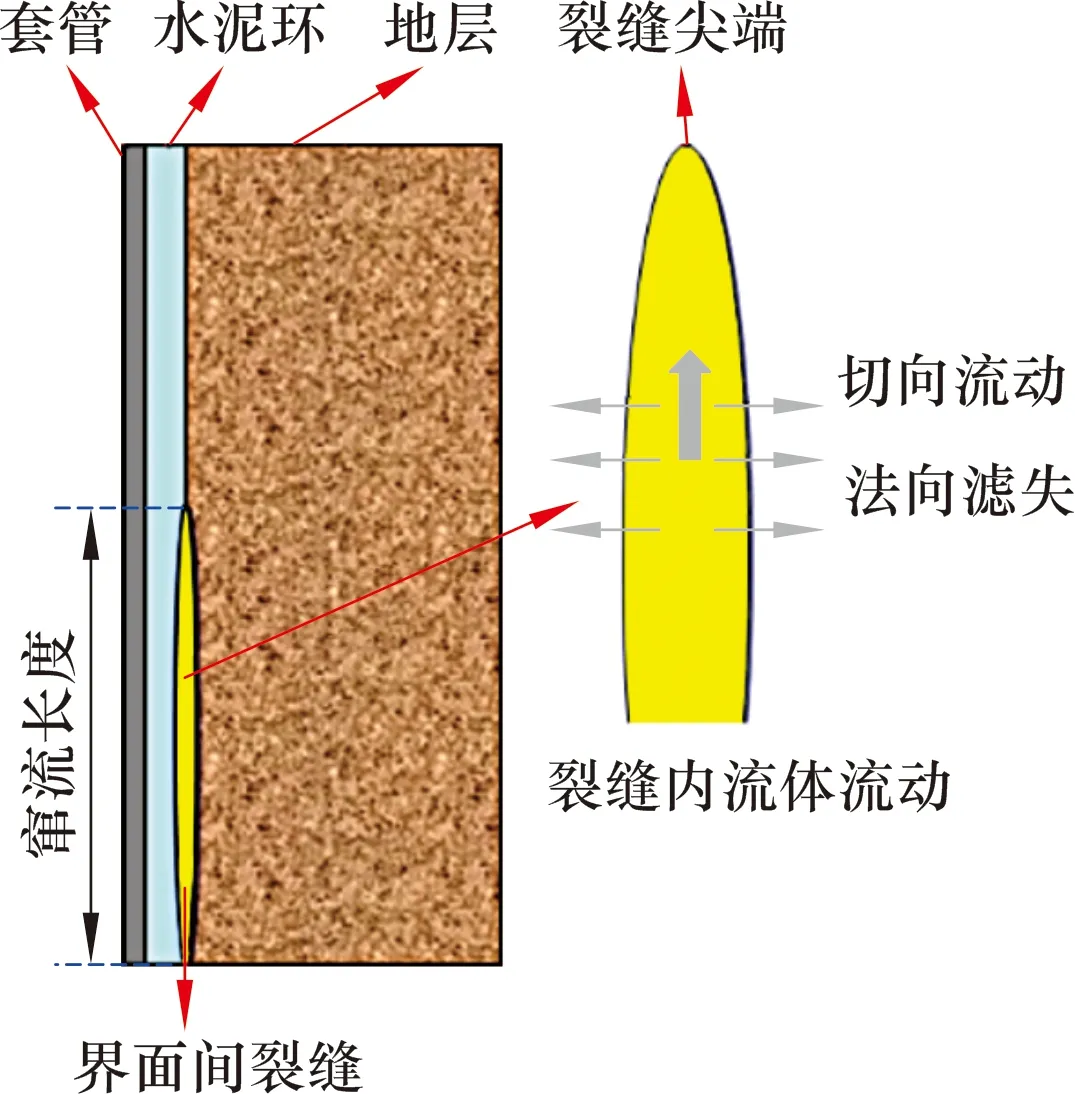
图1 水泥环-地层界面间流体流动示意图Fig.1 Schematic diagram for fluid flow at cement sheath-formation interface

假设流体为不可压缩的牛顿流体，则Cohesive单元界面中切向上单位长度的体积流量向量qf可表示为[12]：

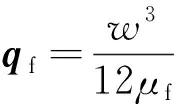
(1)

式中：w为界面张开厚度，m；pf为界面中流体压力，Pa；μf为界面中压裂液黏性系数，Pa·s。

界面内流体法向流速为[7]：

(2)

式中：pt为界面上表面的孔隙压力，Pa；ct为界面上表面的滤失系数，m/(Pa·s)；pb为界面下表面的孔隙压力，Pa；cb为界面下表面的滤失系数，m/(Pa·s)；vt、vb为流体在界面上、下表面的法向流速，m/s。

1.2 流固耦合作用控制方程

假设水泥环和地层均为多孔介质，多孔介质中固体骨架的平衡方程为[13]：

(3)

流体在多孔介质中的连续性方程可表示为[14]：

(4)

式中：nw为孔隙比，无因次；x为空间向量，m；ρw为流体密度，kg/m3；vw为流体渗流速度，m/s；J为多孔介质体积变化比率；t为时间，s。

多孔介质中的流体服从达西定律，其流速为[15-16]：

(5)

式中：g为重力加速度，m/s2；k为有效渗透流量矩阵，m/s。

1.3 Cohesive单元的损伤模型

根据FENG Y.C.等[9]的研究，最大名义应力准则能够更加安全地预测界面间裂缝的发展。因此，本文采用最大名义应力准则判断水泥环界面的损伤。当发生损伤时，需满足的条件为：

(6)

(7)

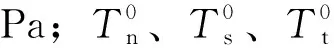
损伤开始后界面刚度降低，当界面刚度下降为1时，界面完全损伤。本文采用基于能量标准的BK断裂准则来评估水泥环界面裂缝的损伤演化，具体表达式为：

(8)

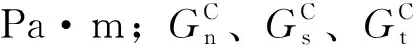
2 有限元模型

2.1 模型建立

以水平井某压裂段为研究对象，用ABAQUS软件建立尺寸为2 m×2 m×20 m的水泥环界面窜流模型，如图2所示。

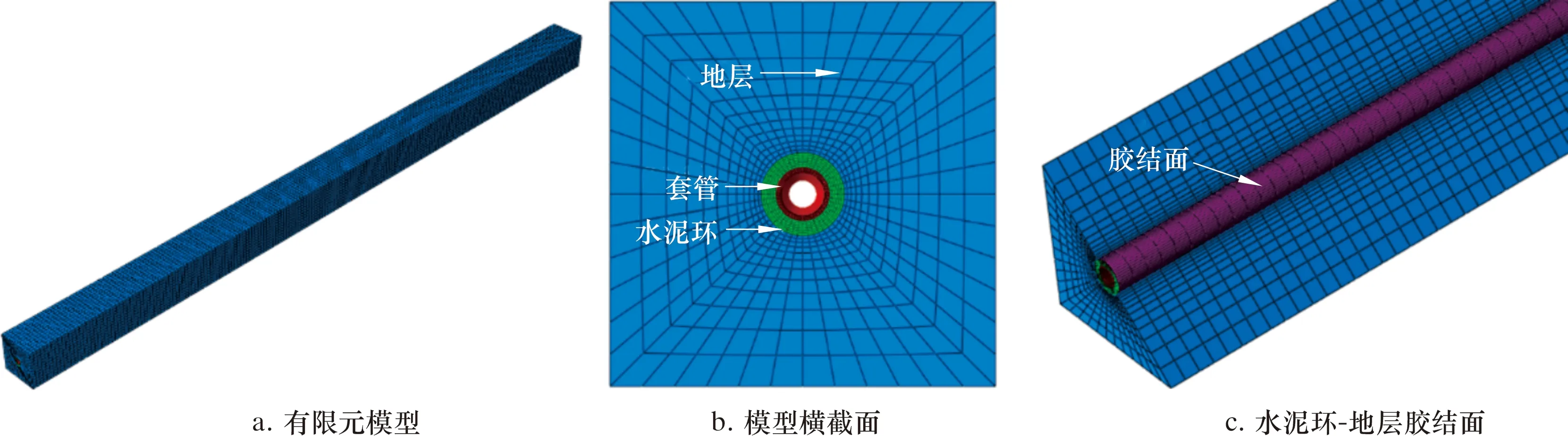
图2 水泥环界面窜流模型Fig.2 Interfacial channeling model of cement sheath

模型中的水泥环、地层均为弹塑性多孔材料，套管为线弹性材料。在套管-水泥环、水泥环-地层界面插入Cohesive单元，Cohesive单元的属性即代表水泥环界面的胶结性能[17-18]，Cohesive单元的刚度退化即表示界面发生脱黏。当流体侵入水泥环界面时，Cohesive单元刚度退化的长度即表示流体侵入的长度。分别在套管-水泥环、水泥环-地层界面的右侧预设2个破坏单元，以此表示因射孔或固井质量差导致的水泥环界面的初始缺陷。2个破环单元中间预设一个流体侵入点，压裂液从该点侵入水泥环界面。采用结构化网格和过渡网格的形式对模型进行网格划分，从而提高模型的计算精度及速度。

2.2 模型验证

B.LECAMPION等[6]通过试验得到了水泥环-地层界面裂缝脱黏的几何形状，FENG Y.C.等[9]的计算结果与试验对比，已经被验证是准确的。本文所建模型采用FENG Y.C.等[9]的计算参数，模拟水泥环界面的脱黏过程，以验证模型的准确性。

图3表示侵入点流体压力随时间的变化情况。从图3可见，流体压力迅速增加到峰值，然后下降到一个相对恒定的值。峰值压力对应于裂缝扩展的开始，通常称为裂缝破裂压力(FBP)。相对恒定的压力意味着裂缝已达到稳定扩展阶段，通常将其定义为裂缝扩展压力(FPP)。从图3可以看出，FENG Y.C.等[9]计算出的裂缝破裂压力为20.7 MPa，裂缝扩展压力为17.1 MPa；本文模型计算出的裂缝破裂压力为21.6 MPa，裂缝扩展压力为17.9 MPa。经过比较可知，模型误差在5%以内，表明本文所建模型能够较为准确地模拟水泥环界面的窜流现象。

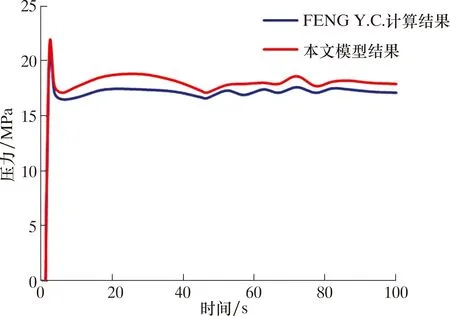
图3 数值模型与FENG Y.C.计算结果对比Fig.3 Comparison of numerical model and FENG Y.C. calculation results

2.3 水泥环两界面窜流对比分析

FENG Y.C.等[9]研究了水泥环-地层界面脱黏的情况，并未考虑水泥环-套管界面脱黏的情况，因此，本文在保证参数不变的情况下，在相同材料属性、相同载荷以及相同边界条件下，研究水泥环-套管界面和水泥环-地层界面发生窜流的难易程度，对比结果如图4所示。

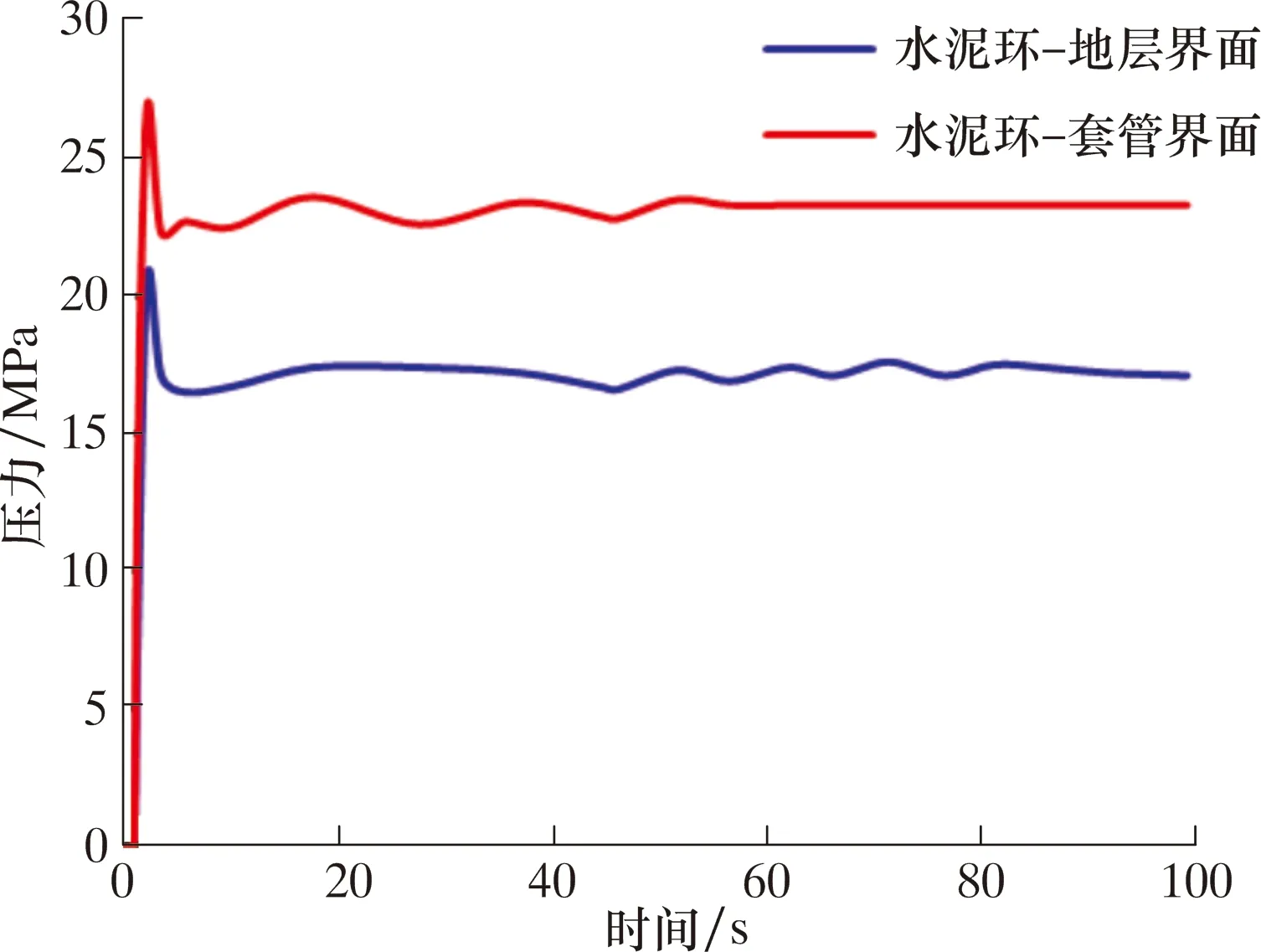
图4 水泥环两界面窜流对比分析Fig.4 Comparative analysis on channeling at 2 interfaces of cement sheath

从图4可以看出：水泥环-地层界面的裂缝扩展压力为17.1 MPa，裂缝破裂压力为21.6 MPa；而水泥环-套管界面的裂缝扩展压力为22.6 MPa，裂缝破裂压力为26.8 MPa。因此，水泥环-地层界面比水泥环-套管界面更容易发生窜流。接下来以水泥环-地层界面为主进行研究。

3 实例分析

3.1 概况

本文以四川盆地泸州区块某井为研究对象，该井有1个试油层，分26段，段长43～109 m，平均段长64.23 m；每段射孔3～9簇，共150簇，段内簇间距在8.0～14.5 m之间，平均簇间距10.6 m。压裂资料显示，第23段压裂段出现了明显的压窜现象，因此以该压裂段为研究对象建立有限元分析模型。

该压裂段的最大水平地应力为95.8 MPa，最小水平地应力为83.7 MPa，垂向应力为89.9 MPa，初始地层压力为72.88 MPa，套管内压为77 MPa，压裂液侵入水泥环界面的流速为1×10-5m3/s。水泥塞-地层界面设置为黏结属性，内聚力刚度为8.5 GPa，黏结强度为0.42 MPa，界面断裂能为100 J/m2，界面间流体滤失系数为5.897×10-14m/(s·Pa)，流体黏度为0.001 mPa·s。地层、水泥环和套管的材料属性如表1所示。

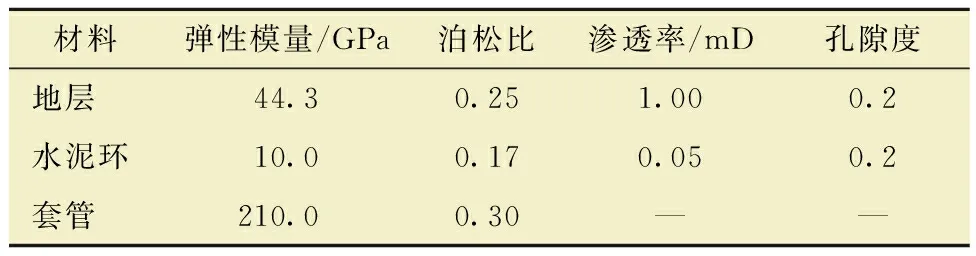
表1 材料属性Table 1 Material properties

3.2 结果分析

模型采用如下2个分析步：①地应力平衡分析步，平衡地应力、孔隙压力以及套管内压，时间设置为1 s；②水泥环-地层界面剥离分析步，模拟压裂液侵入界面初始缺陷处并发生积聚，当积聚的能量超过界面的临界断裂能时，水泥环-地层界面开始脱黏，压裂液继续向前发生窜流。该分析步时间设置为600 s，由此可计算出压裂液注入点处随该分析步时间变化的流体压力，以及界面刚度退化指数。当刚度退化指数为1时，界面完全脱黏，刚度退化长度即代表压裂液的窜流长度。模拟结果如图5所示。

图5 窜流长度随时间的变化情况Fig.5 Variation of channeling length with time

图6表示压裂液初始侵入点处流体压力随时间的变化情况。横坐标为水泥环-地层界面剥离分析步的时间长度。从图5和图6中可以看出，水泥环-地层界面的裂缝破裂压力为41.4 MPa，裂缝扩展压力为36.1 MPa，压裂液窜流长度为6.8 m，第23压裂段的最小簇间距为8.5 m，因此该压裂段虽然会发生窜流，但不会发生簇间窜流，能够保证压裂的正常进行。

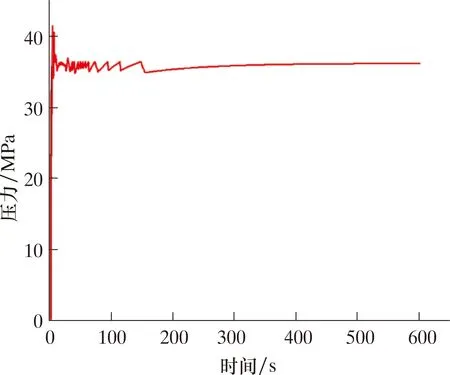
图6 压裂液侵入点处流体压力随时间的变化曲线Fig.6 Variation curve of fluid pressure at fracturing fluid invasion point with time

3.3 敏感性分析

3.3.1 水泥环弹性模量

图7和图8表示水泥环弹性模量对水泥环-地层界面窜流的影响。

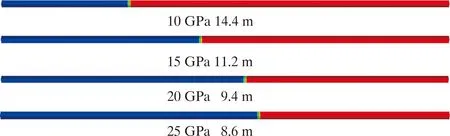
图7 不同水泥环弹性模量下界面窜流长度Fig.7 Interfacial channeling length under different elastic moduli of cement sheath

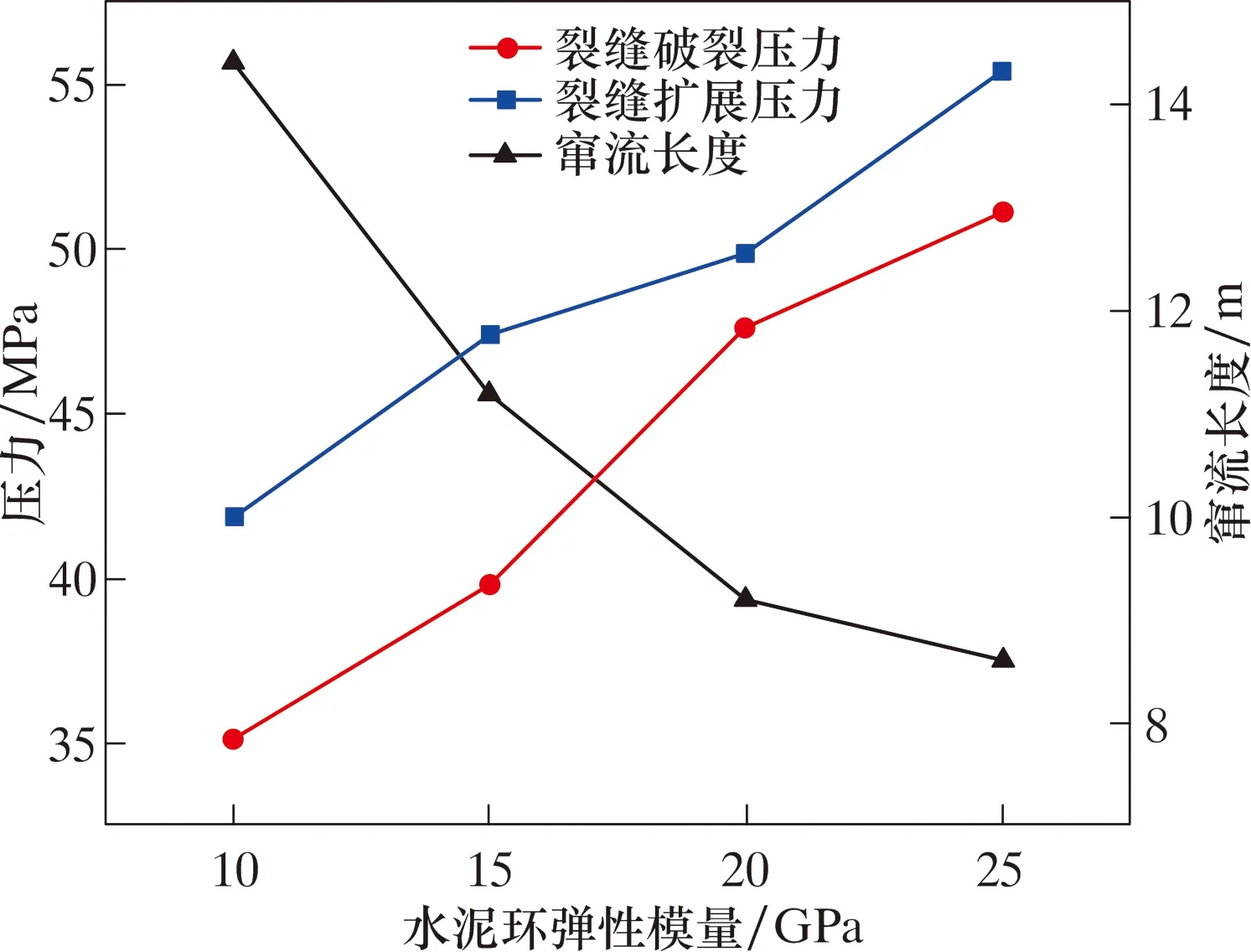
图8 不同水泥环弹性模量下界面裂缝扩展压力、破裂压力和窜流长度Fig.8 Interfacial fracture propagation pressure，breakdown pressure and channeling length under different elastic moduli of cement sheath

由图7和图8可以看出，当弹性模量从10 GPa增大到25 GPa时，界面的窜流长度从14.4 m减小到8.6 m，界面的裂缝破裂压力从41.9 MPa增大到55.4 MPa，界面的裂缝扩展压力从35.1 MPa增大到51.1 MPa。结果表明较大的水泥环弹性模量可以增强水泥环界面的抗窜能力，这是因为水泥环的弹性模量越大，其变形能力就越低，水泥环界面张开的位移就越小。

3.3.2 水泥环泊松比

图9和图10表示水泥环泊松比对水泥环-地层界面窜流的影响。

图9 不同水泥环泊松比下界面窜流长度Fig.9 Interfacial channeling length under different Poisson’s ratios of cement sheath

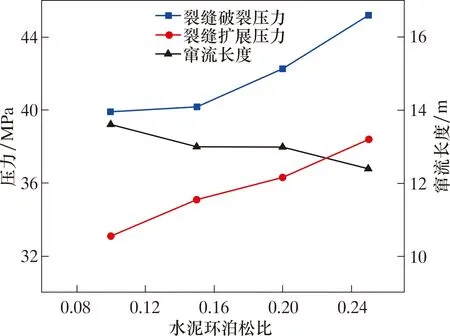
图10 不同水泥环泊松比下界面裂缝扩展压力、破裂压力和窜流长度Fig.10 Interfacial fracture propagation pressure，breakdown pressure and channeling length under different Poisson’s ratios of cement sheath

由图9和图10可知，当水泥环泊松比从0.10增加到0.25，界面的窜流长度从13.6 m减小到12.4 m，界面的裂缝破裂压力从39.9 MPa增加到45.2 MPa，界面的裂缝扩展压力从33.1 MPa增加到38.4 MPa。结果表明水泥环泊松比越大，其抗窜能力越强，但影响程度较低。

3.3.3 压裂液侵入流速

图11和图12表示不同压裂液侵入流速对水泥环-地层界面窜流的影响。

图11 不同压裂液侵入流速下界面窜流长度Fig.11 Interfacial channeling length under different invasion flow rates of fracturing fluid

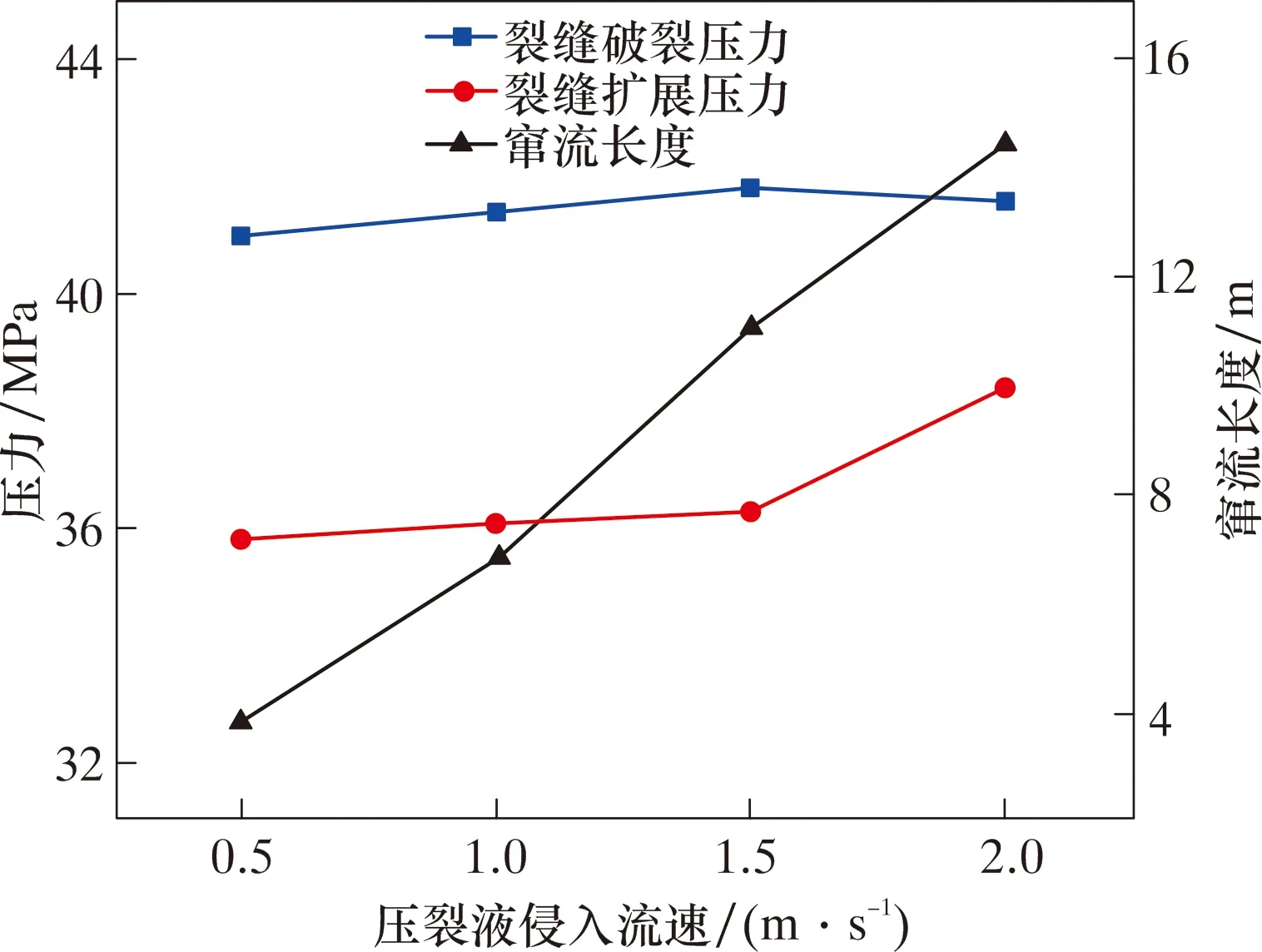
图12 不同压裂液侵入流速下界面裂缝扩展压力、破裂压力和窜流长度Fig.12 Interfacial fracture propagation pressure，breakdown pressure and channeling length under different invasion flow rates of fracturing fluid

由图11和图12可以看出，当压裂液侵入流速从0.5 m3/s增大到2.0 m3/s，界面的窜流长度从3.8 m增加到14.4 m，界面裂缝的破裂压力和扩展压力无明显变化。结果表明，压裂液侵入流速越大，界面的窜流长度越大，而压裂液侵入流速与排量相关。因此，在压裂施工的过程中若检测到窜流的发生，在保证压裂正常进行的同时，应适当降低排量来降低窜流的风险。

4 结 论

(1)利用ABAQUS软件，基于Cohesive单元方法，建立了水泥环界面窜流模型，并对比水泥环-套管界面和水泥环-地层界面的窜流情况。结果表明，水泥环-地层界面更容易发生裂缝扩展，该界面更容易发生窜流。

(2)结合现场实例，某井在压裂过程中存在窜流现象，利用本文模型进行窜流分析，模拟出了压裂液的窜流长度，水泥环-地层界面剥离的裂缝扩展压力以及裂缝破裂压力，所得结论可为现场施工提供借鉴。

(3)水泥环弹性模量对水泥环界面窜流的影响较大，增大水泥环的弹性模量有利于降低窜流的风险；水泥环泊松比对窜流的影响较小。

(4)在压裂施工的过程中若检测到窜流的发生，可以在保证压裂正常进行的同时，适当降低施工排量来降低窜流的风险。