基于SSA VMD LSTM NKDE的短期风电功率概率预测
高晓芝 郭旺 郭英军 宋静冉 孙鹤旭
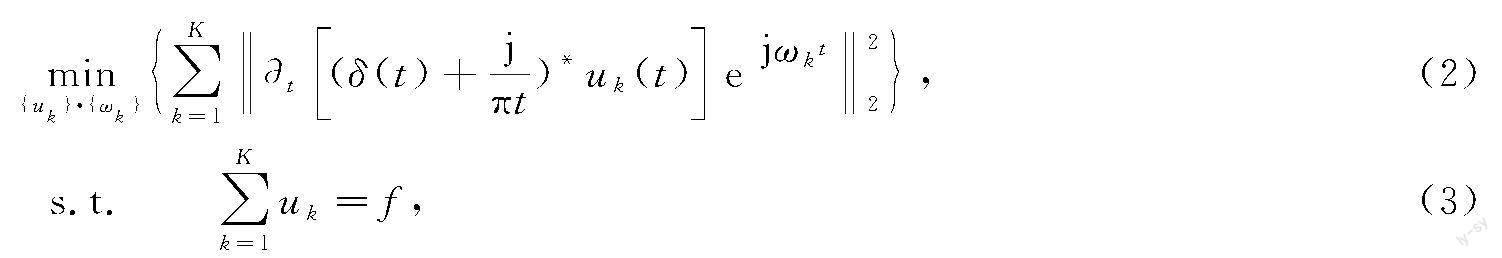


摘 要:
为进一步提高风电功率预测精度,提出一种基于麻雀搜索算法(SSA)优化VMD参数的组合预测方法。首先,使用麻雀搜索算法对VMD参数进行优化,并利用优化后的VMD对数据进行分解;其次,结合灰色关联分析法和熵权法对环境变量进行相关性分析,选择相关性最高的影响因素与分解得到的各模态分量组合作为LSTM预测模型的输入,获得更为精确的预测结果;最后,建立基于非参数核密度估计(NKDE)的风电功率概率预测模型,实现对风电功率预测结果不确定性的有效量化。结果表明,所提组合模型的MAE,RMSE和MAPE比VMD LSTM模型的分别下降了39.51%,33.22%和4039%。SSA VMD LSTM NKDE组合模型不仅能够有效提高确定性预测的精度,而且还能够实现对风电功率預测结果不确定性的有效量化,为风电功率预测提供了科学决策依据。
关键词:风能;麻雀搜索算法;变分模态分解;熵权法;灰色关联分析;组合预测模型
中图分类号:TM614 文献标识码:A DOI:[WTBZ]10.7535/hbkd.2023yx04001
Short term wind power probabilistic forecasting based on SSA VMD LSTM NKDE
GAO Xiaozhi1, GUO Wang1,2, GUO Yingjun1, SONG Jingran1, SUN Hexu1
(1. School of Electrical Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China;2.Renqiu Power Supply Branch, State Grid Hebei Electric Power Company Limited, Renqiu, Hebei 062550, China)
In order to further improve the accuracy of wind power forecasting, a combined forecasting method based on sparrow search algorithm (SSA) optimizing variational mode decomposition (VMD) parameters was proposed. Firstly, the SSA was used to optimize the VMD parameters, then the optimized VMD was used to decompose the data. Secondly, the entropy weight method and grey relational analysis were combined to analyze the correlation of environmental variables, and the combination of the most relevant influencing factors and the decomposed modal components were selected as the input of the LSTM prediction model to obtain more accurate prediction results. Finally, a wind power probability prediction model based on NKDE was established to effectively quantify the uncertainty of wind power prediction results. The results show that the MAE, RMSE and MAPE of the proposed combination model decrease by 3951%, 3322% and 4039%, respectively, compared with the VMD LSTM model. The SSA VMD LSTM NKDE combination model can not only effectively improve the accuracy of deterministic prediction, but also effectively quantify the uncertainty of wind power prediction results, which provides scientific decision making basis for wind power prediction.
Keywords: wind energy; sparrow search algorithm; variational mode decomposition; entropy weight method; grey relational analysis; combined prediction mode
在“双碳”目标驱动下,构建以新能源为主体的新型电力系统成为必然趋势。近年来,风能在全球电力生产结构中的占比持续增加,然而风能的不稳定性给电网的安全稳定运行带来了巨大挑战[1]。高精度的功率预测不仅能有效减少电力系统备用容量配置,提高风电机组的控制功率,缓解电网调峰压力,还能提供未来某一时刻风电功率的波动区间,为电力系统提供更全面的预测信息,以便更加灵活可靠地进行调度安排[2] 。
近年来,循环神经网络(RNN)因具有记忆功能、深度表达能力,能够挖掘数据中的时序信息,在电力系统典型的时间序列预测中得到充分利用[3],作为高效循环神经网络代表的长短期记忆网络(LSTM),通过特殊化的结构设计可有效避免传统RNN在训练过程中出现的梯度消失以及梯度爆炸问题,从而更适用于电力系统相关数据预测[4 6] 。文献[7]提出一种基于长短期记忆神经网络的风功率预测模型,结果证明长短期记忆神经网络模型的预测精度比支持向量机模型高,具有较高的应用价值。由于预测模型的精确程度与输入数据的质量息息相关[8],因此对数据进行合理的处理与分解能够提升预测模型的学习效果。国内外许多研究者从信号分解重构的角度进行研究,以降低其不平稳性,从而提高预测精度。常用的分解方法有经验模态分解(EMD)[9]、集合经验模态分解(EEMD)[10]和变分模态分解(VMD)[11]等。EMD不仅解决了小波基选取与确定分解尺度困难的问题[12],还保留了小波多分辨的优势,可用于风速时间序列的分析。文献[13]提出一种基于EMD的短期风功率预测方法,利用EMD对历史数据进行分解降噪,从而达到提高预测精度的效果。但经验模态分解在形成固有模态函数时,会出现信息特征提取混淆的问题。EEMD通过噪声辅助信号处理有效解决了这一问题。文献[14]利用EEMD将原始风速序列划分为几个固有模态函数,形成一个潜在的特征集,然后通过迭代过程自动生成更合适的子特征集,最后通过相应的机器学习模型进行预测。尽管EEMD改善了EMD分解时模态混叠现象,但在分解时添加白噪声的幅值难以确定,过低将无法抑制混叠现象,过高又会出现较多的伪分量[15]。VMD可以将复杂序列分解为幅值频率可调的若干信号[16],克服了集合EMD频率特征不易分辨等问题,实现信号的准确分解,运算效率更高。文献[17]利用VMD非递归性的优势,对原始数据进行分解,通过与其他模型对比,表明VMD分解能够有效提取风功率序列的细节信息。需要指出的是,VMD在分解前需人为设定一些参数值,为了避免取值不当带来的影响,可通过优化算法确定最优参数组合,从而提高预测精度。一些文献中已经提出了采用不同的优化算法,如粒子群优化算法(PSO)[18]、鲸鱼优化算法(WOA)[19]和麻雀优化算法(SSA)[20]来优化VMD参数,但研究成果大多应用在故障诊断的特征参数提取方面,在功率预测研究中应用较少。相比PSO容易早熟收敛,WOA易陷入局部极值,导致精度不高等问题,SSA搜索精度高、收敛速度快、稳定性好,而且克服了容易陷入局部最优的问题。
综上,本文拟综合考虑风速、风向和温度等多种环境因素的影响,针对在传统VMD算法中因参数设置不当导致信号欠分解或过分解的问题,引入SSA算法对VMD的关键参数进行优化,通过灰色关联度分析法和熵权法筛选出相关性最高的环境影响因素,提出一种基于SSA VMD LSTM的组合预测模型,并采用非参数核密度估计(NKDE)分析SSA VMD LSTM模型的预测误差分布,然后计算给定置信度下的预测区间,最后通过实际数据验证所提模型的有效性和优越性。
1 基于SSA优化VMD参数
1.1 VMD算法原理
VMD算法本质上是一个变分问题,能很好地处理非线性数据问题。该模型通过交替方向乘子法和迭代更新计算最优解,将复杂信号分解为多个振幅和频率可调的信号(IMF)。IMF可用作FM AM信号,其表达式为
uk(t)=Ak(t)cos[φk(t)] ,(1)
式中Ak(t)是瞬时振幅函数,相位函数φk(t)是非递减的,因此有ωk(t)=φ′k(t)≥0,定义ωk(t)为uk(t)的瞬时频率。
利用Hilbert变换计算模态函数的解析信号,得到单边频谱。将分解后的信号与其中心频率混合,并将每个模态频谱转换为基频频率[21]。根据调制信号梯度方向的平方L2范数对各模态的带宽进行估计,其表达式为
式中:{uk}为分解得到的K个模态分量;{ωk}为各分量的中心频率;*为卷积符号;δ(t)为狄克拉函数。
引入二次惩罚因子α和拉格朗日乘法算子λ,将约束变分问题转变为非约束变分问题[22] :
利用交替方向乘子迭代算法更新un+1k,ωn+1k和λn+1k求解上式“鞍点”,即为约束变分模型的最优解。
1.2 麻雀搜索算法优化VMD参数
由VMD算法特点可知,模态个数K和二次惩罚因子α需在分解前进行预设,如果参数设置不当,可能会出现信号欠分解或过分解问题,从而影响预测精度。如果采取局部寻优的方式,即只考虑单个影响因素,将另一个参数设置为常数,就会忽略两者之间的交互作用。因此,本文采用SSA算法对VMD的参数进行寻优,消除人为设定参数的主观影响。SSA是一种受麻雀觅食和反捕食行为启发的新型群体优化算法[23 24]。在觅食过程中,一部分麻雀是发现者身份,另一部分是追随者身份,二者可以根据能量储备量的多少相互转换,但所占比例不变,发现者具有较好适应度值且具备较高的储备量,其任务是寻找食物,为整个种群提供觅食方向,追随者则是通过发现者来获取食物。迭代过程中,发现者的位置更新规则如下:
式中:Xp是目前发现者占据的最优位置;Xworst是当前全局最差位置;A是一个满足A+=AT(AAT)-1的矩阵;c为麻雀个数。当意识到危险时,麻雀种群会做出反捕食行为,意识到危险的麻雀在整个种群中随机产生,其数学模型如下:
式中:Xbest是当前全局最优位置;β是一个随机数,作为步长控制参数;ε是避免分母为零的最小常数;Q∈[-1,1],是一个随机数,表示麻雀移动的方向,也是步長控制参数;fi是此时麻雀个体的适应度值;fg是此时全局最佳的适应度值;fworst是最差的适应度值。
采用SSA对VMD参数进行优化时,应先确定适应度函数,本文以样本熵作为SSA优化的适应度函数,熵值越小,分量频率越明显,模态混叠现象越弱,其定义为
SampEn(data,q,r)=ln Bq(r)-ln Bq+1(r) ,(8)
式中:data为随机信号时间序列;q为嵌入维度;r为相似性容限;B为2个向量在相似容限r下匹配q或(q+1)个实数的概率。
SSA优化VMD参数流程如图1所示。
2 熵权 灰色关联度分析
由于使用单一的关联度分析指标不能准确刻画风电功率的规律性及相关性[25],本文采用灰色关联度分析法和熵权法[26]组合分析不同环境变量与风电功率间的相关性,从而得出影响风电功率的主要因素和次要因素,选取主要影响因素作为预测模型的输入。
将风电功率数据作为参考序列记为X0(k)=[X0(1),X0(2),…,X0(n)],环境特征数据作为比较列记为Xi(k)=[Xi(1),Xi(2),…,Xi(n)]。熵权 灰色关联度分析步骤如下。
步骤1 变量的无量纲化。选用均值化处理,将数量级大的序列均值归一化到1的量级附近,见式(9)。
步骤2 求差序列、最大差和最小差。
Δi(k)=|X′0(k)-X′i(k)| ,(10)
Δmax=maximaxk|X′0(k)-X′i(k)| ,(11)
Δmin=minimink|X′0(k)-X′i(k)| 。(12)
步骤3 计算关联系数。ρ为分辨系数,一般取0.5。
3 基于SSA VMD LSTM NKDE的概率预测
3.1 非参数核密度估计理论
非参数核密度估计(NKDE)是概率论中用来估计未知参数概率密度函数(PDF)的一种非参数化估计方法。根据风电场相关历史数据信息,通过核密度估计就可以得到变量分布,不需要对样本分布进行任何假设,常被用于风电或光伏预测等领域的概率预测分析。
针对一组样本数为n的风电功率预测误差数据p={p1,p2,…,pn},其密度函数为f(p)=F(p),由NKDE方法对p的分布估计为
式中h为窗宽,用来决定误差数据分布的区间划分。
当样本量足够大且窗宽趋于0时,基于非参数核密度估计的风电功率预测误差的概率密度函数为
式中:pi为第i个样本;函数K(p,h)为核函数。
在NKDE方法中,窗宽和核函数是2个关键参数。其中,窗宽h用来决定误差数据分布的区间划分,设置过小,易受单个样本点的影响,导致局部波动特征明显从而影响估计模型的分布情况;选择过大,会使所得的PDF过于平滑,导致预测误差的概率密度分布与实际情况不符。核函数的选取也会直接影响NKDE方法的密度曲线光滑程度及拟合程度,从而影响结果的精确度。常用于NKDE的核函数如表1所示。
3.2 概率预测步骤
由于风电功率具有波动性,为降低原始风电功率数据对预测精度产生的影响,本文采用VMD对原始数据进行分解;为避免在分解时出现信号欠分解或过分解现象, 采用SSA优化VMD参数,从而降低预测误差。结合灰色关联度分析法和熵权法对环境变量进行相关性分析,然后将相关性最高的影响因子和VMD分解得到的各模态分量组合作为LSTM预测输入,利用NKDE方法对SSA VMD LSTM模型的误差进行分析,得到相应的概率密度曲线,最后综合确定性预测结果和误差分布结果,确定出某一置信区间下的预测区间。風电功率概率预测具体步骤如下:
步骤1 对原始风电数据进行归一化处理;
步骤2 利用SSA算法优化VMD参数,获得最优参数组合;
步骤3 利用SSA VMD将风功率序列分解为K个模态分量;
步骤4 利用熵权 灰色关联度分析法对环境特征变量做相关性分析;
步骤5 将相关性最高的影响因子与VMD分解得到的模态分量分别进行组合;
步骤6 分别对步骤5中的组合序列建立LSTM预测模型,并将各序列的预测值进行整合,得到最终确定性预测值;
步骤7 统计确定性预测误差,采用NKDE方法确定概率密度函数;
步骤8 设置一定比例的置信度(1-α),得到该置信度下误差波动区间[Fα/2,F(1-α)/2];
步骤9 结合相应的确定性预测结果,构造概率预测区间。
SSA VMD LSTM NKDE模型的预测流程如图2所示。
4 算例分析
4.1 评价指标
平均绝对误差(MAE),是实际值和预测值之间绝对误差的平均值,其表达式为
风电功率概率预测方法的评价指标主要包含可靠性和敏锐度2个方面。目前较为常见的用来评价可靠性的指标为预测区间覆盖率(PICP),其值越大表示实际风电功率点落入预测区间的个数越多,但过大的区间覆盖率不具有研究价值;用预测区间平均宽度(PINAW)来反映敏锐度,即区间预测结果的平均带宽,在同等置信水平下其值越小越好。
PICP计算公式:
式中:N为样本总数;ci是区间上限Ui和区间下限Li对实际值的可靠性指标,若真实值落入[Li,Ui]内,则ci=1,反之ci=0。
PINAW计算公式:
通过预测区间平均宽度的指标,能够有效避免因预测区间过于强调可靠性而导致预测区间的范围过大,致使不能有效地获取决策信息。当PICP一定时,PINAW越小,说明预测区间越窄,预测效果越好,但过于保守的锐度指标不利于决策者对不确定性进行评估,从而导致系统运行的经济性降低。
温克勒得分(Score):
式中:vi=Ui-Li。
Score是一项综合评价预测区间覆盖率和宽度的指标,可以用来反映整体的预测效果,它是非正的,结果越接近0值,表明预测效果越好。
4.2 基于SSA VMD的风电功率分解结果
实验选取河北省某风电场2018 07 01至2018 07 31的风电机组实测数据,时间间隔15 min,共3 000个样本点。由于风电功率波动、数据采集误差以及随机噪声的存在严重影响了预测模型的精确度,因此需要对原始数据进行分解。本文采用VMD对原始数据进行分解,从而降低数据的复杂度,但在传统的VMD算法中,K和α的取值不当会导致原始信号欠分解或过分解,因此本文提出用SSA优化VMD参数模型。图3为VMD分解结果,K=4,α=2 000;图4为SSA优化VMD后分解结果,K=8,α=2 371。
从图中对比可以看出,经过优化后分解数据的非线性降低,局域变化波动趋于平缓,通过将随机性较强的原始风电数据分为低频和高频子序列,有助于提高模型预测精度,其中低频子序列能够反映原数据的整体波动趋势,高频子序列能够体现对应时刻的细节信号和噪声信号。将图4中的模态分量进行Hilbert变换即可得到其边际谱,如图5所示。
图5 SSA VMD分解IMF边际谱
Fig.5 SSA VMD decomposition IMF spectrum
图6 不同优化算法适应度曲线变化趋势
Fig.6 [WB]Variation Trend of fitness curve of
[DW]different optimization algorithms
圖7 预测结果对比图
Fig.7 Comparison of prediction results
由图5可知,经SSA VMD分解得到的8个模态分量的频率区分较为明显,且分解后的每个IMF既保持了原始风电功率序列的特征又抑制了模态混叠。由此可见,经SSA优化后的VMD更有利于提高风电功率预测精度。图6为不同优化算法对VMD参数进行优化时适应度值对比结果,从中可以看出,粒子群算法在第17次迭代时出现最小适应度值0.674 1,萤火虫算法在第14次迭代时出现最小适应度值0.673 4,鲸鱼优化算法在第12次迭代时出现最小适应度值0.672 9,SSA算法随迭代次数增加迅速收敛,在第8次迭代时达到最小适应度函数值0.672 5,验证了SSA算法的优越性。
4.3 基于相关性分析的预测结果
本文使用河北省某实际风电场的数据,结合风力发电特征,选取风速、空气密度、风向、温度和气压作为风电功率的影响因子,按熵权 灰色关联度分析法的计算步骤,求得各个气象因素与风电功率的相关程度分别为风速0.981、空气密度0853、风向0.871、气压0.612、温度0.537。可见,风速对风电功率预测的影响程度最大,其次是风向、空气密度、气压、温度。因此选取风速作为预测模型的输入。图7为考虑风速影响和剔除风速影响时的预测结果对比图,从中可以看出剔除风速后,预测误差明显增大。
4.4 不同模型预测结果对比分析
实验选取3 000个样本点,其中的前90%用于训练,后10%用于测试。在LSTM中,输入层时间步数表示进行功率预测的历史数据序列长度,其数值的确定需要考虑模型训练的有效性以及历史信息的完备性[27] ;输入层维数则是各个 IMF 分量的输入变量;隐藏层数目即是 LSTM 层的个数,增加隐藏层数可提高模型的非线性拟合能力,但同时也使模型更复杂,预测时间随之增加,甚至引发过拟合问题,因此本文将隐藏层数选择的范围控制在2层内;LSTM输出为功率值,故输出变量维数为1。学习率初始值设置为0.005,梯度阈值设置为1。为验证该模型的有效性,本文分别搭建BP,SVM,ELM,LSTM,EMD LSTM和VMD LSTM模型进行对比,为保证客观性,各预测模型的参数均通过多次尝试实验选取最佳值。误差指标如表2所示,对比结果如图8—图10所示。
表2 不同模型误差评估表
Tab.2 Error evaluation of different models
预测模型
MAE
RMSE
MAPE/%
BP
8.310 4
9.874 3
11.237 0
ELM
7.835 1
8.267 7
9.043 7
SVM
6.082 3
7.310 4
7.490 6
LSTM
4.531 9
5.994 2
6.755 3
EMD LSTM
3.021 4
4.170 9
4.910 6
VMD LSTM
2.189 6
3.287 6
3.274 5
SSA VMD LSTM
1.324 4
2.195 3
1.963 4
图8 单一模型预测结果对比图
Fig.8 Comparison of prediction results of single model
图9 未优化模型预测结果对比图
Fig.9 Comparison of prediction results of unoptimized model
图10 优化后模型预测结果对比图
Fig.10 [WB]Comparison of prediction results of
[DW]optimized models
从图8预测曲线和表2误差指标对比来看,LSTM的预测效果更好,相比于BP,ELM和SVM模型,MAE, RMSE和MAPE均有所下降,这是由于LSTM模型具有长时记忆特性,可以利用数据的时间序列性,有效避免了风电数据的波动性。图9为LSTM,EMD LSTM和VMD LSTM的模型预测结果对比图,从图9预测曲线和表2误差指标对比来看,经过数据分解后预测效果明显比未对数据进行分解的预测效果好,说明LSTM的精确程度与输入数据的质量息息相关。与EMD LSTM相比,VMD LSTM模型的MAE,RMSE和MAPE分别下降了27.53%,21.18%和33.32%,表明VMD分解降噪效果比EMD好,更适合处理时序信息的预测工作。图10为VMD LSTM和SSA VMD LSTM模型预测结果对比图,从图10预测曲线和表2误差指标对比来看,经过参数优化后再进行VMD分解的预测精度比直接用VMD进行分解的预测精度要高,SSA VMD LSTM模型的MAE,RMSE和MAPE比VMD LSTM的分别下降了39.51%,33.22%和40.39%。实验表明,采用SSA对VMD算法中的参数进行寻优,能够有效降低因参数设置不当导致信号欠分解或过分解问题对预测效果的影响。
4.5 概率预测结果
利用NKDE方法对SSA VMD LSTM模型的确定性预测误差进行分析,采用渐进积分均方误差(AMISE)来计算窗宽h,当使用高斯核函数时,窗宽的计算可简化为h=1.06σn-1/5。为验证NKDE方法的优越性,将其与假定Gamma分布的参数估计方法进行对比分析,基于SSA VMD LSTM模型预测误差的NKDE方法和基于Gamma分布估计方法的PDF如图11所示。
由图11可知,采用NKDE方法得到的PDF具有更好的拟合效果,更符合实际风电功率预测的误差分布。采用Gamma分布得到的PDF在波峰附近的拟合度明显不够,虽然Gamma概率密度曲线相比NKDE方法的概率密度曲线平滑,但与实际误差分布差别较大,因此采用NKDE方法对确定性预测误差分布的描述更加准确。通过对图11中采用NKDE方法拟合得到的PDF求积分,可得到对应的累积概率密度函数(CDF),從而获得给定置信度下的误差分布边界,具体如图12所示。从中可以得出,在不同置信度下风电功率预测误差的上下界,本文取分位点为α/2=5%和α/2=10%,即可得到置信度为90%和80%下的风电功率波动区间,不同置信度下的风电功率概率预测结果如图13所示。
在图13中,对比不同置信度下的风电功率概率预测结果可以看出,随着置信度的降低,实际风电功率点落在概率预测区间内的概率越小。为了能够更加直观地对参数化估计方法和非参数化估计方法的概率预测性能进行评价,选取PICP,PINAW和Score 3种常用于风电功率概率预测的评价指标来衡量概率预测的效果,概率预测结果评价指标如表3所示。
由表3可知,在置信度一定的条件下,NKDE的覆盖率均高于Gamma分布方法的覆盖率,且在置信度为90%和80%时都满足覆盖率大于预设置信度下的覆盖率。但随着置信度的降低,预测区间覆盖率也降低,由此可见,若预测区间太宽,会出现过于保守现象。通过PINAW指标能够有效衡量预测区间的敏锐性,避免了因预测区间过于强调可靠性而导致预测区间过宽,失去参考价值。本文所用的NKDE
方法比Gamma分布方法的预测区间平均宽度窄,说明在一定置信度下,采用NKDE方法的概率预测结果更贴近真实值,预测效果更好,且在置信度为90%和80%时的PINAW值均符合短期预测中预测区间平均宽度,应在30%~50%的要求。但在相同置信度下,PICP随PINAW的增大而增大。当PINAW一定时,PICP越大越好;当PICP一定时,PINAW越小,表明预测区间更逼近实际功率值,预测效果越好。仅有PICP和PINAW不能全面评价概率预测性能,因此引入Score评价指标。采用NKDE方法的Score指标的绝对值均小于采用Gamma分布方法的Score指标的绝对值。结果表明,采用NKDE方法的概率预测效果更好。
5 结 论
针对VMD分解方法参数人为设置难以达到最优的问题,提出了一种基于SSA VMD LSTM NKDE的组合风电预测模型。结合灰色关联度分析法和熵权法对环境变量进行相关性分析,选择相关性最高的影响因素与SSA VMD分解得到的各模态分量组合作为LSTM模型的输入,并建立了基于NKDE的风电功率概率预测模型,实现对风电功率预测结果不确定性的有效量化。通过算例对比分析,得出以下结论。
1)采用SSA优化VMD参数可有效搜索得到最优参数组合。算例分析表明,与PSO和WOA等参数优化算法相比,SSA算法更易于跳出局部最优,收敛速度更快。
2)采用熵权 灰色关联度分析风功率环境变量的相关性方法能够客观有效地对风电功率的影响因素进行评估,得出风速是影响因子最高的因素的结论。算例表明,是否考虑风速输入影响因素将直接影响风电功率预测精度。
3)采用SSA VMD LSTM组合预测模型能够有效提升短期风电功率预测精度,与未优化的预测模型相比,所提方法的MAE,RMSE和MAPE均有所降低,验证了该组合预测模型的有效性。
4)在风电功率点预测的基础上建立了基于NKDE的风电功率概率预测模型。与假定Gamma分布的参数化方法对比结果表明,基于NKDE的风电功率概率预测结果更可靠和更敏锐,而且在给定置信度下均满足短期风电功率预测的要求,具有一定的实际工程意义。
本文不足之处在于仅针对单风电场功率预测展开研究,下一步将针对大规模风电集群开展区域多风电场功率预测研究。
参考文献/References:
王伟胜,王铮,董存,等.中国短期风电功率预测技术现状与误差分析[J].电力系统自动化,2021,45(1):17 27.
WANG Weisheng,WANG Zheng,DONG Cun,et al.Status and error analysis of short term forecasting technology of wind power in China[J].Automation of Electric Power Systems,2021,45(1):17 27.
[2] 孙荣富,张涛,和青,等.风电功率预测关键技术及应用综述[J].高电压技术,2021,47(4):1129 1143.
SUN Rongfu,ZHANG Tao,HE Qing,et al.Review on key technologies and applications in wind power forecasting[J].High Voltage Engineering,2021,47(4):1129 1143.
[3] SHAO Haijian,DENG Xing,JIANG Yingtao.A novel deep learning approach for short term wind power forecasting based on infinite feature selection and recurrent neural network[J].Journal of Renewable and Sustainable Energy,2018,10(4).DOI: 10.1063/1.5024297.
[4] QIN Yong,LI Kun,LIANG Zhanhao,et al.Hybrid forecasting model based on long short term memory network and deep learning neural network for wind signal[J].Applied Energy,2019,236:262 272.
[5] ZHANG Yongzhi,XIONG Rui,HE Hongwen,et al.Long short term memory recurrent neural network for remaining useful life prediction of lithium ion batteries[J].IEEE Transactions on Vehicular Technology,2018,67(7):5695 5705.
[6] 康田雨,覃智君.基于超參数优化和双重注意力机制的超短期风电功率预测[J].南方电网技术,2022,16(5):44 53.
KANG Tianyu,QIN Zhijun.An ultra short term wind power forecasting method based on hyperparameter optimization and dual stage attention mechanism[J].Southern Power System Technology,2022,16(5):44 53.
[7] 王炜,刘宏伟,陈永杰,等.基于LSTM循环神经网络的风力发电预测[J].可再生能源,2020,38(9):1187 1191.
WANG Wei,LIU Hongwei,CHEN Yongjie,et al.Wind power forecast based on LSTM cyclic neural network[J].Renewable Energy Resources,2020,38(9):1187 1191.
[8] 史加荣,赵丹梦,王琳华,等.基于RR VMD LSTM的短期风电功率预测[J].电力系统保护与控制,2021,49(21):63 70.
SHI Jiarong,ZHAO Danmeng,WANG Linhua,et al.Short term wind power prediction based on RR VMD LSTM[J].Power System Protection and Control,2021,49(21):63 70.
[9] DU Pei,WANG Jianzhou,YANG Wendong,et al.A novel hybrid model for short term wind power forecasting[J].Applied Soft Computing,2019,80:93 106.
[10]LIN Guancen,LIN Aijing,CAO Jianing.Multidimensional KNN algorithm based on EEMD and complexity measures in financial time series forecasting[J].Expert Systems with Applications,2021,168.DOI: 10.1016/j.eswa.2020.114443.
[11]HU Huanling,WANG Lin,TAO Rui.Wind speed forecasting based on variational mode decomposition and improved echo state network[J].Renewable Energy,2021,164:729 751.
[12]ABEDINIA O,LOTFI M,BAGHERI M,et al.Improved EMD based complex prediction model for wind power forecasting[J].IEEE Transactions on Sustainable Energy,2020,11(4):2790 2802.
[13]王佶宣,鄧斌,王江.基于经验模态分解与RBF神经网络的短期风功率预测[J].电力系统及其自动化学报,2020,32(11):109 115.
WANG Jixuan,DENG Bin,WANG Jiang.Short term wind power prediction based on empirical mode decomposition and RBF neural network[J].Proceedings of the CSU EPSA,2020,32(11):109 115.
[14]CHEN Yaoran,DONG Zhikun,WANG Yan,et al.Short term wind speed predicting framework based on EEMD GA LSTM method under large scaled wind history[J].Energy Conversion and Management,2021,227.DOI: 10.1016/j.enconman.2020.113559.
[15]NAIK J,SATAPATHY P,DASH P K.Short term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression[J].Applied Soft Computing,2018,70:1167 1188.
[16]DRAGOMIRETSKIY K,ZOSSO D.Variational mode decomposition[J].IEEE Transactions on Signal Processing,2014,62(3):531 544.
[17]盛四清,金航,刘长荣.基于VMD WSGRU的风电场发电功率中短期及短期预测[J].电网技术,2022,46(3):897 904.
SHENG Siqing,JIN Hang,LIU Changrong.Short term and mid short term wind power forecasting based on VMD WSGRU[J].Power System Technology,2022,46(3):897 904.
[18]NA Wu,ZHENG XIAN Yang,SHU XIAN Fan.Extraction method and application of traveling wave natural frequencies based on PSO and VMD[C]//2020 Chinese Automation Congress (CAC).Shanghai:IEEE,2020:28 34.
[19]张萍,张文海,赵新贺,等.WOA VMD算法在轴承故障诊断中的应用[J].噪声与振动控制,2021,41(4):86 93.
ZHANG Ping,ZHANG Wenhai,ZHAO Xinhe,et al.Application of WOA VMD algorithm in bearing fault diagnosis[J].Noise and Vibration Control,2021,41(4):86 93.
[20]XUE Jiankai,SHEN Bo.A novel swarm intelligence optimization approach:Sparrow search algorithm[J].Systems Science & Control Engineering,2020,8(1):22 34.
[21]SUN Zexian,ZHAO Mingyu.Short term wind power forecasting based on VMD decomposition,ConvLSTM networks and error analysis[J].IEEE Access,2020,8:134422 134434.
[22]NAIK J,DASH S,DASH P K,et al.Short term wind power forecasting using hybrid variational mode decomposition and multi kernel regularized pseudo inverse neural network[J].Renewable Energy,2018,118:180 212.
[23]YAN Pengcheng,SHANG Songhang,ZHANG Chaoyin,et al.Research on the processing of coal mine water source data by optimizing BP neural network algorithm with sparrow search algorithm[J].IEEE Access,2021,9:108718 108730.
[24]WUMAIER T,XU Chang,GUO Hongyu,et al.Fault diagnosis of wind turbines based on a support vector machine optimized by the sparrow search algorithm[J].IEEE Access,2021,9:69307 69315.
[25]HAN Min,ZHANG Ruiquan,QIU Tie,et al.Multivariate chaotic time series prediction based on improved grey relational analysis[J].IEEE Transactions on Systems,Man,and Cybernetics:Systems,2019,49(10):2144 2154.
[26]YANG M S,NATALIANI Y.A feature reduction fuzzy clustering algorithm based on feature weighted entropy[J].IEEE Transactions on Fuzzy Systems,2018,26(2):817 835.
[27]胡威,张新燕,李振恩,等.基于优化的VMD mRMR LSTM模型的短期负荷预测[J].电力系统保护与控制,2022,50(1):88 97.
HU Wei,ZHANG Xinyan,LI Zhenen,et al.Short term load forecasting based on an optimized VMD m RMR LSTM model[J].Power System Protection and Control,2022,50(1):88 97.

