基于离散元模型的岩石Ⅱ型断裂研究
张加明 曹卓康 付岩 刘丰

摘 要:为了解决岩石Ⅱ型断裂韧度的准确测量问题,提高对工程裂隙岩体稳定评价的可靠性,采用颗粒离散单元法,从微观裂纹、声发射及块体特征角度出发,结合断裂韧度计算,对短芯压缩(SCC)试样进行了数值研究。结果表明:随着切槽间距比(C/H)的增加,试样破坏模式会由纯剪向拉剪混合过渡;声发射模式前震 主震 后震型(C/H≥0.3)的转变与块体破坏特征也验证了这一结果;当C/H=0.2时,计算所得的断裂韧度与室内试验测得的值相符,验证了所采用方法对于Ⅱ型断裂韧度测试的准确性。借助离散单元法阐明了短芯压缩试样的破裂特征,从裂纹扩展的角度明确了切槽间距变化对破坏形态及破坏模式影响的规律,可为实验室精确测量岩石Ⅱ型断裂韧度提供参考。
关键词:岩土力学;Ⅱ型断裂韧度;离散元;裂纹扩展;破裂过程;微裂纹
中图分类号:TU455 文献标识码:A DOI:10.7535/hbkd.2023yx04008
Study on rock mode Ⅱ fracture based on discrete element model
ZHANG Jiaming1,2,CAO Zhuokang1,2, FU Yan1,2,LIU Feng1,2
(1.School of Civil Engineering,Tianjin University,Tianjin 300072,China; 2. State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China)
Abstract: In order to solve the problem of accurate measurement of rock mode Ⅱ fracture toughness and improve the reliability of stability evaluation of engineering fractured rock mass, a detailed numerical study of short core compression (SCC) samples was carried out from the perspective of micro crack, acoustic emission and block characteristics, combined with fracture toughness calculation by particle discrete element method. The results show that the failure mode of the sample changes from pure shear to tension shear mixture with the increase of the ratio of slot spacing (C/H). The foreshock mainshock aftershock (C/H≥0.3) transformation and block failure characteristics of acoustic emission models also confirm the result. When C/H=0.2, the calculated fracture toughness is consistent with that measured in laboratory experiment, which verifies the accuracy of mode Ⅱ fracture toughness test in this case. With the help of discrete element method, the fracture characteristics of short core compression samples are elucidated, and the effect of groove spacing on the failure form and failure mode is determined from the angle of crack growth, which could provide some reference for accurate measurement of rock mode Ⅱ fracture toughness in lab.
Keywords: rock and soil mechanics; mode Ⅱ fracture toughness; discrete element; crack growth; fracture process; micro crack
在隧道、采礦与建筑等岩土工程活动中,承载岩体及硐室围岩的稳定性受到岩体物理力学性质的影响[1]。岩体的断裂特征影响内部裂隙的扩展与破坏方式,对岩爆、冲击地压与边坡工程的成因机理分析起主导作用[2 4]。因此,分析岩体的断裂特征对保证工程建设的可靠性与安全性评价具有重要意义。
断裂模式[1]主要分为3种:Ⅰ型断裂(张开破坏)、Ⅱ型断裂(剪切破坏)和Ⅲ型断裂(撕裂破坏)。与金属、陶瓷等材料不同,工程岩体内部裂纹的破坏形式受拉伸破坏较少,而受压缩载荷下的Ⅱ型剪切破坏占主导[3],因此对岩体的Ⅱ型断裂韧度的测量有重要意义。目前,已经有很多学者对断裂韧度的测量提出了试验方法。XIE等[5]和AYATOLLAHI等[6]通过改变半圆盘弯曲(SCB)试样的切口角度和加载方式,可实现由Ⅰ型破坏向Ⅱ型破坏的转变,测得Ⅱ型断裂韧度。BACKERS等[7 8]提出了基于岩芯试样的冲切剪切(punch through shear,PTS)试样方法,成为国际岩石力学与工程学会(ISRM)推荐的Ⅱ型断裂测试方法。在此基础上,YAO等[9]借助PTS试样研究了岩石断裂韧度随围压变化下的动态力学特性。考虑到PTS试样制备的复杂性与加载装置的特殊性,JUNG等[10]提出了短芯压缩(short core in compression,SCC)试样,具有可实现围压的加载、切槽的简易制作和测试的便利性等优势。大量学者针对SCC试样开展了变形场[11]、围压特性[12]研究,发现随着轴向应力与围压的增加,其剪切区域内损伤增加,并且岩石的动态Ⅱ型断裂韧度呈现增加趋势。XU等[13]基于有限元方法借助切槽尖端二次裂纹法计算了Ⅱ型断裂强度因子和断裂韧度,得到了SCC试样的应力强度因子与几何参数Y之间的关系,并将SCC的试验结果与PTS进行对比,验证了试验的可靠性。除此之外,国际岩石力学学会推荐了其他测试Ⅱ型断裂的方法,如常用于弯曲梁的反对称四点弯曲(ASFPB)[14]、双边切口半对称加载[15]和易于制作与加载的直切槽巴西圆盘(CSTBD)[16]和短块压缩(SBC)[17]等。
上述岩石的Ⅱ型断裂韧度测定,试验尺度无法直观精确地观测到微观裂纹起裂、发育与贯通的过程,难以对试样的破裂形式进行划分。而离散单元法可展现出试样微观界面上裂纹从连接到破坏的扩展全过程[18],对分析岩石Ⅱ型断裂破裂形式具有可行性。离散单元法(DEM)最初是由CUNDALL等[19]提出,可以有效模拟岩体试样的变形、颗粒破坏的萌生、发育和发展过程,在研究岩土破坏细观机理上有着明显的优势,在地质[20]、岩土[21]和矿冶[22]等领域得到了广泛的应用。WU等[23]和YOON等[24]使用离散元对PTS试样进行模拟,研究了加载速率和围压变化对应力强度因子的影响。模拟结果显示,PTS试样的剪切破裂常伴随着拉伸翼裂纹的发育,而随着围压的增加,拉伸裂纹的发育受到抑制。
研究切槽间距变化对断裂韧度测量结果精确性的影响,将为工程应用中地下洞室开挖、矿产开采等活动稳定性与安全性评估提供有效手段。当前对SCC断裂形式的研究均为对宏观破坏裂纹分析的常规试验,岩石内部微观裂纹的发育过程与宏观裂纹的关系尚不明确,切槽间距的变化对断裂发育过程和破坏模式的影响也有待研究,断裂韧度的准确测量难以保证。因此,本文借助颗粒离散单元法,从微裂纹发育、声发射及块体特征的角度出发,研究5种切槽间距(10,20,30,40和50 mm)下SCC试样的断裂过程及规律,揭示切槽间距比变化对试样微观裂纹的发育过程及破坏模式的影响,并通过断裂韧度的计算,验证SCC试样对Ⅱ型断裂韧度测量的有效性。
1 颗粒黏结模型与离散元参数标定
1.1 颗粒黏结模型
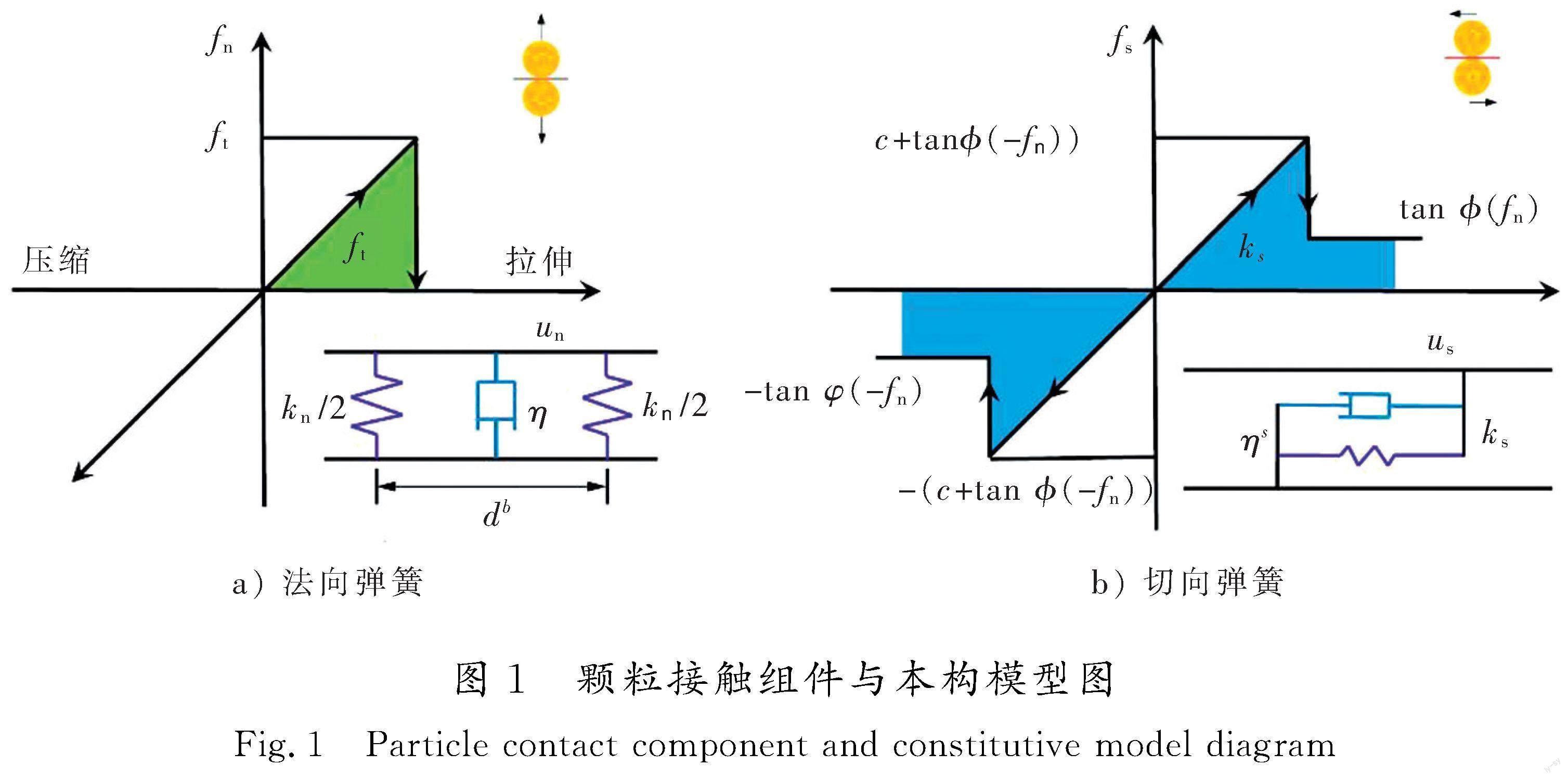
离散单元法(DEM)的本构模型定义了颗粒接触变形和颗粒接触力之间的关系,还影响DEM模型的计算能力。本文使用开源离散元程序DICE2D[25]进行岩石Ⅱ型断裂破裂形式研究。DICE2D黏结颗粒接触模型[26]的力学组件如图1所示,主要包含弹簧与缓冲器元件。弹簧元件表示加载力与位移的变化呈线性关系;而缓冲器则提供速度阻尼,反映加速度项,具有一定的率效应,能够反映出能量的耗散。其中法向弹簧被分解为2个相互距离为db的子弹簧,该模型可以视作POTYONDY等[27]提出的键模型的简化版本。当db非零时,黏结模型可传递力矩,否则退化为经典的库伦接触模型。切向弹簧的分布对力矩计算无影响,因此只施加1个弹簧与缓冲器。
当颗粒间拉应力超过黏结强度即Fn>ft时,连接键破坏形成拉伸裂纹;当颗粒间剪应力超过剪切强度即Fs>c+tan φ(-fn),连接键破坏形成剪切裂纹,黏聚力c变为0,但颗粒间仍保留有一定强度。其中Fn和Fs为接触对所受拉应力与剪应力,受拉为正,受压则为负。
1.2 微观与宏观参数的标定
DICE2D将大量颗粒组合来表征材料,其宏观岩石强度与黏结特征是由微观颗粒参数决定的。因此,对试验模型进行计算前模型的微观参数标定是模拟的重点与难点。在宏观力学试验中研究的参数主要是:1)弹性参数(弹性模量E和泊松比υ);
2)强度参数(单轴抗压强度与抗拉强度)。而在DICE2D程序中,定义的是颗粒间的微观接触参数。同样的,微观参数也可划分为弹性参数(法向刚度kn、切向刚度ks)和强度参数(拉伸强度σt、黏聚力σs、内摩擦角φ)。
标定过程中,主要借助单轴压缩与巴西劈裂试验。DICE2D建模采用的是动态平衡法,该方法首先根据设定的颗粒尺寸和孔隙率,在给定区域内生成随机颗粒,然后通过颗粒的动态平衡不断迭代,调整颗粒位置,最后通过将部分颗粒放大来消除悬浮颗粒。考虑到结果的精确度与计算效率问题,通过对颗粒粒径大小的调节,实现最终建立模型的颗粒直径在0.3~0.6 mm间,呈正态分布,单轴压缩颗粒数目20 657,巴西劈裂颗粒数目22 468。在单轴压缩试验中,分别在模型的4个方向布置了如图2所示的测点,用于监测随应力加载试样的轴向与径向变形。分析单轴压缩试验的应力应变曲线的线弹性加载段,则可确定弹性参数(E,υ);应力曲线的峰值则对应单轴抗压强度。同理,将同样的微观参数代入至巴西劈裂试验即可得到宏观的拉伸强度。
使用试错法进行参数标定[28],过程如下。首先根据弹性模量设定初始Kn与真实数据在同一数量级,并将Ks/Kn设定为较为常见值0.4。根据泊松比调节Ks/Kn的比值,使得计算的泊松比满足精度要求。强度参数一般选择与实际相符,黏聚力数倍于拉伸强度。然后固定Ks/Kn,由弹性模量确定出Kn。在弹性參数标定完后,利用单轴压缩与巴西劈裂实验标定强度参数。通过不断试算,使得拉伸强度、单轴压缩强度和破坏模式都能吻合,最终得到一套满足要求的微观参数。标定过程中,在考虑1个微观参数的影响时,其他微观参数值是固定的。
参照文献[12]和文献[13]中的房山大理岩试样,通过标定以获得目标微观参数,开展准静态加载下的单轴压缩与巴西劈裂模拟试验。最终目标是实现所建立的颗粒模型模拟试验参数与宏观参数的一致。标定试验中单轴压缩试验与巴西劈裂试验模拟破裂模式如图3所示,主要为典型的X型剪切破坏与单一的拉伸裂纹破坏。单轴压缩试样与巴西劈裂试样的应力应变曲线如图4所示,试样加载曲线经历压密、弹性、塑性阶段后达到峰值产生破坏,峰值后强度迅速下降。
通过试错法得到最终标定的微观参数如表1所示。表2为试样模型的宏观力学参数与文献[13]中房山大理岩的实际宏观试验力学参数对比结果。从表2中的数据可以看出,标定所得参数在单轴抗压强度、抗拉强度、弹性模量和泊松比方面的误差率均小于0.75%,完全满足后续模拟精度要求,可以进行下一步的模拟计算。
1.3 试验方案
对5种切槽间距下SCC试样进行模拟,分析其在不同切槽间距下微裂纹的发育过程及破坏形式的转变。使用标准的静态SCC试样尺寸如图5 a)所示。试样高度×宽度为100 mm×50 mm,切槽缝宽度t=1 mm,切槽深度a=25 mm。C为切槽之间的距离,H为试样高度。C/H为切槽间距与高度的比值,用于表示切槽间距的变化。模拟了5种切槽间距(C=10,20,30,40,50 mm)下的试样工况。
建立的SCC颗粒模型如图5 b)所示,各工况下试样模型由布尔运算划分的边界,在动态平衡法下填充了数量在2.5万左右、直径0.3~0.6 mm、呈正态分布的离散颗粒,在模型切槽缝隙(1 mm)附近的颗粒分布均匀且密集。在数值模拟加载过程中,与试样相接触的为顶端与底端2面加载墙体,侧向无墙体约束或加载。设置颗粒与墙体接触参数,使得墙体以 0.01 m/s 的恒定速度向下移动,时间步长为10-8 s,加载直至试样发生破坏。通过记录墙体所受压力的大小,并计算接触面积的比值即可得到试样所受应力数值。
2 模拟结果
2.1 微裂纹破裂过程分析
基于各切槽间距下SCC试样的模拟结果,分析切槽间距变化影响下的微裂纹破裂发育过程及破坏模式特点。通过模拟结果可知,裂纹扩展有明显的阶段性,而且通过对比发现在60%,80%,100%峰值及70%峰后应力状态下试样裂纹发育阶段性明显。因此,为便于描述裂纹扩展的发育特点,选取了图6所示的应力 位移曲线(a)—(e) 5个阶段,分别表征了0,60%,80%,100%峰值和70%峰后应力状态下试样裂纹扩展情况。
图7展示5种不同切槽间距下SCC试样的破坏过程,其中黄色为微观拉伸裂纹,红色为微观剪切裂纹。依据微裂纹扩展发育过程的模拟结果,破坏形式可分为2类:剪切破坏与拉伸 剪切混合破坏。
当C/H分别为0.1,0.2和0.3时,呈现出剪切破坏模式。SCC试样沿着上下切槽尖端间剪切面发育主破裂面,而当C/H=0.3时在剪切面右侧平面出现拉伸微裂纹。从图7(b)到图7(c)的变化过程可看出,裂纹较为均匀地分布于切槽尖端间的剪切平面,并随着加载密度的增加而增加。黄色的拉伸微裂纹发育较红色的剪切微裂纹分布广泛,这是由于微观裂纹与宏观破坏之间的差异性。袁康等[29]的分析是“压致拉”导致剪切模式下颗粒间产生拉伸微裂纹。随着加载的进行,在峰前(c)和(d)阶段裂纹急剧发展,峰后(e)应力阶段裂纹发育减缓。
当C/H为0.4,0.5时,呈现拉剪混合破坏形式。对于C/H=0.4,试样首先在切槽对侧方向发育拉伸微裂纹,随后(c)阶段在切槽尖端伴生拉伸与剪切微裂纹,且拉伸微裂纹多于剪切微裂纹,并最终在(d)和(e)阶段发育贯通的剪切微裂纹。表明先后发生了拉伸破坏与剪切破坏,试样的破坏形式为Ⅰ型+Ⅱ型的混合破坏。当C/H=0.5时,试样在(b)到(c)阶段同样发育向内扩散的拉伸微裂纹,(d)阶段在切槽端部的竖直与斜向下45°方向发育拉伸微裂纹,(e)阶段发育沿剪切面的贯穿剪切破坏微裂纹。此时出现竖直发育的拉伸裂纹,是由于切槽端离加载面较近,竖直应变在水平位置上的不均匀性造成右侧位移大于左侧。
从微裂纹扩展特点可见,剪切破坏裂纹发育集中于剪切平面,次生裂纹不发育或较少。混合破坏则可分为水平拉伸裂纹发育、竖直拉伸裂纹发育和贯穿剪切裂纹发育阶段。混合型破坏显然不符合Ⅱ型断裂测量要求,因此在试验过程中应确保试样满足剪切破坏要求。
2.2 声发射破坏分析
声发射(acoustic emission, AE)是指材料局部因能量快速释放而释放出瞬态弹性波的现象[30]。岩石试样在受到外力作用时,其自身裂隙与微观结构的损伤往往伴随着声发射事件的产生。声发射技术作为一种实时性与高灵敏度的监测手段,可捕捉到岩石试样损伤发育与失稳破坏的全过程信息,已在岩土领域得到了广泛的应用[31]。依据DICE2D中颗粒间的接触方式及本构原理,微观颗粒受力破坏后会生成拉伸与剪切裂纹,相应的即为一次应变能释放,因此每一步的损伤行为都得到记录。而通过记录微观裂纹生成的位置与时步,并对单位时间内的事件数与全过程事件总数进行处理,即可得到试样破裂全过程下的声发射事件分布特征。
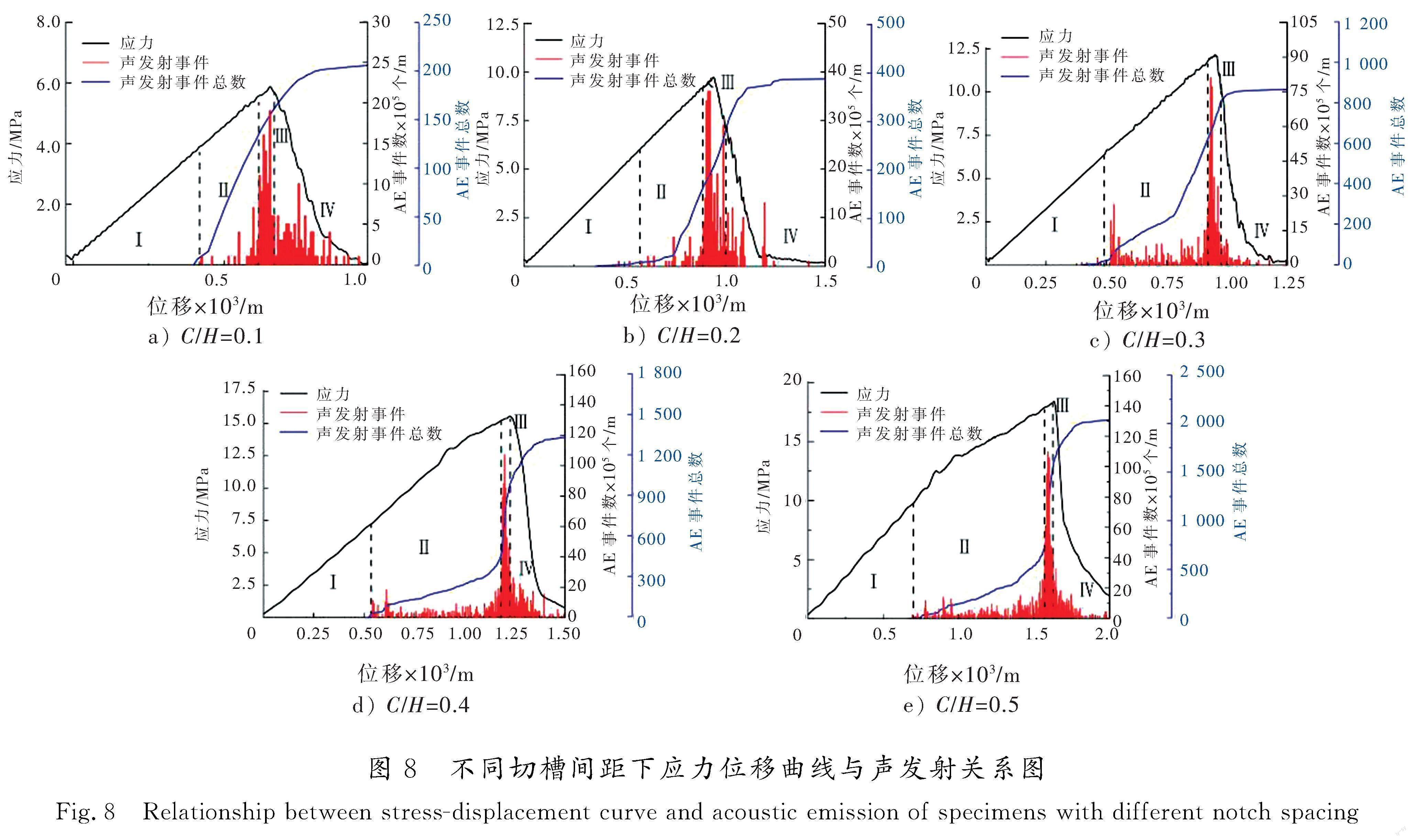
不同切槽间距下试样的应力 声发射事件关系如图8所示。由图8可知,试样裂纹的起始、发育与贯通过程中声发射事件呈现阶段性。图8中可将声发射事件分为4个阶段:Ⅰ平静阶段、Ⅱ缓慢发展阶段、Ⅲ峰值加速阶段和Ⅳ峰后下降阶段。平静阶段试样处于弹性压缩阶段,无微观裂纹与声发射事件产生。缓慢发展阶段开始出现零散的频率较小的声发射事件,试样内部产生初始微裂纹,对应了2.1节中裂纹发育的(b)与(c)阶段。在90%峰值应力处,声发射事件急剧增加,此时裂纹处于非稳定扩展的峰值加速阶段。声发射事件在峰值应力处达到最大值,随后呈下降趋势直到试样峰后阶段贯通破坏。本文研究声发射事件的發育规律与李浩然等[30]使用不同尺寸比的花岗岩试样试验得到的声发射事件数值变化特征相符合。
试样的声发射事件随切槽间距的增加表现出显著的差异性。C/H≥0.3情况试样的缓慢发展阶段较C/H≤0.2情况分布区域占比明显增长,前者约在40%峰值应力进入缓慢发育阶段,而后者在50%左右。从图8可看出,C/H≤0.2情况以单峰值事件为主,而C/H≥0.3情况下声发射事件在主峰值前发育有次峰值,并在达到峰值后事件迅速减小。依据声发射的模式分析,当C/H≤0.2时声发射模式为主震 后震型,而当C/H≥0.3时转变为前震 主震 后震型。与2.1节中C/H≥0.3试样的裂纹发育阶段相对应,次峰值的声发射事件被认为是试样发育的水平拉伸裂纹,而主峰值的事件为拉伸与剪切的混合破坏,表明试样先发育水平拉伸裂纹后形成混合破坏裂纹。从声发射事件总数曲线中可以看出C/H≥0.3情况下声发射事件出现了近乎竖直的增长阶段,表明混合破坏情况下裂纹发育迅速,形成时间集中。声发射事件的分析与微裂纹的发育相互印证,进一步阐明了切槽间距变化对试样破坏模式转变的影响。
2.3 块体特征破坏分析
模拟结果可识别出分离的块体形状,并赋予不同的颜色。将不同切槽间距下块体模拟结果与试验块体破坏对比分析,结果如图9所示。从图中可以看出,在C/H=0.1~0.3时,模拟得到的试样破裂形成2种颜色,表明试样破坏后形成2个完整的块体,这与XU等[13]试验结果相符。观察剪切面形态及碎裂块体分布可得出,随着切槽间距比的增加,剪切面的形态逐渐偏离竖直平面并且破碎块体颗粒分布愈发不规则。
当C/H=0.4时,试样破裂成为3个主要的块体,在裂纹分析中提到的水平拉伸微裂纹使得试样在水平方向上出现了宏观的拉伸断裂。当C/H=0.5时,试样破裂为4个较大的块体,此时竖直方向上的拉伸裂纹占主导,在竖直方向上分裂出块体,而水平方向破裂的裂纹未能形成较明显的块体分离,此时主要的破裂形式仍然为拉伸破裂与剪切破裂的混合形式。
从不同切槽间距下的SCC试样的破坏形式可看出,当C/H=0.3时,次生裂纹的发育已出现偏离剪切面的趋势,因此不建议采用0.3切槽间距比。对比C/H=0.1和C/H=0.2情况,两者均符合试样剪切破坏的要求,而JUNG等[10]和LI等[11]在对Ⅱ型断裂测量的试验中选取C/H=0.2作为最优试验对象具有充足的合理性。
3 断裂韧度计算
应力强度因子(SIF)是表征脆性材料存在裂纹时裂纹尖端应力场奇异性的特征物理量,是对裂纹分析起关键作用的参数[1]。对于同一种类型的裂纹,裂纹尖端应力场的分布规律是相同的,而裂纹尖端SIF的失稳扩展临界值又可称为断裂韧度。
断裂韧度的准确求解对岩体的破坏分析有重要意义。基于前述破坏特征分析可知,切槽间距比C/H=0.2情况下的试样破裂符合剪切破坏模式。因此,为验证此切槽间距下测定断裂韧度的可行性与准确性,依据离散元模拟计算结果,对SCC试样的断裂韧度进行求解,并将数值与相关研究数据进行对比。
3.1 几何参数求解
SCC试样的Ⅱ型断裂韧度KⅡ可由WATKINS等[32]基于能量分析提出的计算公式(1)求得。
式中:τ=P/DC,为施加在试样断面的应力与受剪切面积相比所得的剪应力,其中P为施加的荷载大小;a为试样的半径;Y(C/H)为几何参数,只与切槽试样的几何形态相关,可由式(2)计算。
通过离散单元法模拟试样的破坏过程,可确定峰值荷载P的值,进而求得剪切应力τ。因此,计算试样断裂韧度需要完成几何参数Y(C/H)的求解。而Y(C/H)的求解通过有限元软件基于边界配置法或权函数法,借助J积分对裂纹尖端的断裂韧度进行计算[33],计算不同长度下的尖端裂纹,可求得切缝尖端无裂纹下的断裂韌度数值。现有成熟的ABAQUS模拟软件可分别建立各切槽间距下的SCC试样模型,并在切槽端部布置预制裂纹求解[13]。对于试样的SIF求解是通过计算不同预制剪切裂纹下的J积分,图10中绘制的积分路径为J积分计算应力强度因子时所取的圆形路径。在1 MPa轴向压力条件下,变换预制裂纹长度绘制趋势线,可得无预制裂纹长度下试样的SIF。
图11为C/H=0.2情况下的裂纹长度与SIF关系直线图。将各断裂韧度的点拟合一条直线,与坐标轴的截距则对应了预制裂纹hc=0 mm情况下的SIF值9.22 MPa·m1/2,将计算结果代入式(2)得到几何参数Y(0.2)=0.415。
需要注意的是本文计算结果与XU等[13]的计算结果Y(0.2)=0.47相比数值偏小,这是因为本文使用的SCC试样尺寸与文献[13]中试样的尺寸大小差异导致的尺寸效应。张盛等[34]和AYATOLLAHI等[35]对断裂试样的尺寸效应所做的研究表明,试样的无量纲参数Y(C/H)与断裂韧度的测试值均会受到尺寸变化的影响。
3.2 断裂韧度求解
将求解所得的几何参数Y(C/H)代入式(1),可得到SCC试样的KⅡC计算公式:
将对应的切槽间距比值、峰值荷载值代入式(3)即可得到试样的Ⅱ型断裂韧度。在此本文使用同种岩石材料参数对冲切剪切(PTS)试样也进行了建模,求解得到了PTS试样的Ⅱ型断裂韧度数值。将使用离散单元法计算得到的断裂韧度与试验测得的结果进行对比,得到房山大理岩断裂韧度计算结果如表3所示。
在模拟中C/H=0.2情况下SCC试样的断裂韧度数值与PTS试样计算数值是相接近的,证明了0.2情况试样确定岩石静态Ⅱ型断裂韧度是有效的。将模拟结果与室内试验相对比,可知模拟建立的模型与试验结果是相接近的,进一步印证了SCC试样对Ⅱ型断裂韧度测量的可行性。
4 结 论
采用颗粒离散单元法,分析了SCC试样的微裂纹发育、声发射规律及块体破坏特征,揭示了切槽间距比变化对试样微观裂纹的发育过程及破坏模式的影响,得到以下结论。
1)随着切槽间距比增加,试样破坏模式由剪切破坏向拉伸 剪切混合破坏转变。在C/H≤0.2时,试样剪切面均匀发育微裂纹最终形成剪切破坏;而C/H≥0.3时呈现拉伸裂纹与剪切裂纹先后发育的混合破坏。
2)试样的声发射事件可分为平静、缓慢发展、峰值加速和峰后下降4个阶段,但C/H≥0.3情况下较C/H≤0.2有更长的缓慢发展阶段,标志着更早的事件起始时间。声发射模式也由C/H≤0.2情况下的主震 后震型转变为C/H≥0.3情况下的前震 主震 后震型,该转变与试样混合破坏中拉伸裂纹的产生相关。
3)试样块体剪切面碎裂形态随切槽间距的增加愈发不规整。试样破裂主体也由C/H≤0.3时的2部分块体转变为C/H≥0.4时的多块块体,这与受混合破坏影响发生不稳定破坏相关。
4)对SCC试样的断裂韧度进行求解,结合冲切剪切(PTS)试样和室内试验测试结果,发现在数值结果上相符合,验证了C/H=0.2情况下SCC试样测量Ⅱ型断裂韧度的有效性与准确性。
本文在对SCC试样的断裂过程及规律研究过程中未施加侧向压力,在后续的研究中,需要考虑围压存在对裂纹发育形式的影响,以满足当前深部岩石的断裂问题研究。
参考文献/References:
[1] 李世愚,和泰名,尹祥础.岩石断裂力学[M].北京:科学出版社,2015.
[2] 谢和平,高峰,鞠杨.深部岩体力学研究与探索[J].岩石力学与工程学报,2015,34(11):2161 2178.
XIE Heping,GAO Feng,JU Yang.Research and development of rock mechanics in deep ground engineering[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(11):2161 2178.
[3] 謝和平,高峰,周宏伟,等.岩石断裂和破碎的分形研究[J].防灾减灾工程学报,2003,23(4):1 9.
XIE Heping,GAO Feng,ZHOU Hongwei,et al.Fractal fracture and fragmentation in rocks[J].Journal of Disaster Prevention and Mitigation Engineering,2003,23(4):1 9.
[4] 何满潮,谢和平,彭苏萍,等.深部开采岩体力学研究[J].岩石力学与工程学报,2005,24(16):2803 2813.
HE Manchao,XIE Heping,PENG Suping,et al.Study on rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2803 2813.
[5] XIE Yousheng,CAO Ping,JIN Jin,et al.Mixed mode fracture analysis of semi circular bend (SCB) specimen:A numerical study based on extended finite element method[J].Computers and Geotechnics,2017,82:157 172.
[6] AYATOLLAHI M R,ALIHA M R M,HASSANI M M.Mixed mode brittle fracture in PMMA an experimental study using SCB specimens[J].Materials Science and Engineering:A,2006,417(1/2):348 356.
[7] BACKERS T,DRESEN G,RYBACKI E,et al.New data on mode Ⅱ fracture toughness of rock from the punchthrough shear test[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(sup1):2 7.
[8] BACKERS T,STEPHANSSON O.ISRM suggested method for the determination of mode Ⅱ fracture toughness[J].Rock Mechanics and Rock Engineering,2012,45(6):1011 1022.
[9] YAO Wei,XU Ying,XIA Kaiwen,et al.Dynamic mode Ⅱ fracture toughness of rocks subjected to confining pressure[J].Rock Mechanics and Rock Engineering,2020,53(2):569 586.
[10]JUNG Y B,PARK E S,KIM H W.Development and application of mode Ⅱ fracture toughness test method using rock core specimen[J].Tunnel and Underground Space,2016,26(5):396 408.
[11]LI Diyuan,ZHANG Chenxi,ZHU Quanqi,et al.Deformation and fracture behavior of granite by the short core in compression method with 3D digital image correlation[J].Fatigue & Fracture of Engineering Materials & Structures,2022,45(2):425 440.
[12]YAO Wei,XU Ying,WANG Chonglang,et al.Dynamic mode Ⅱ fracture behavior of rocks under hydrostatic pressure using the short core in compression (SCC) method[J].International Journal of Mining Science and Technology,2021,31(5):927 937.
[13]XU Ying,YAO Wei,ZHAO Geli,et al.Evaluation of the short core in compression (SCC) method for measuring mode II fracture toughness of rocks[J].Engineering Fracture Mechanics,2020,224.DOI: 10.1016/j.engfracmech.2019.106747.
[14]ALIHA M R M,AYATOLLAHI M R,KHARAZI B.Mode Ⅱ brittle fracture assessment using ASFPB specimen[J].International Journal of Fracture,2009,159(2):241 246.
[15]童谷生,姚良發,徐攀.C40自密实混凝土Ⅱ型断裂韧度的确定[J].力学季刊,2021,42(4):800 810.
TONG Gusheng,YAO Liangfa,XU Pan.Determination of type Ⅱ fracture toughness of C40 self compacting concrete[J].Chinese Quarterly of Mechanics,2021,42(4):800 810.
[16]杨秀锟,谢秦,刘希灵,等.Ⅱ型加载条件下页岩断裂行为的预测研究[J].实验力学,2023,38(1):109 118.
YANG Xiukun,XIE Qin,LIU Xiling,et al.Prediction of shale fracture behavior undermode Ⅱ loading[J].Journal of Experimental Mechanics,2023,38(1):109 118.
[17]FATHIPOUR AZAR H,CHOUPANI N,AFSHIN H,et al.Effect of mineral admixtures on the mixed mode (I/Ⅱ) fracture characterization of cement mortar:CTS,CSTBD and SCB specimens[J].Engineering Fracture Mechanics,2015,134:20 34.
[18]申浩翰,张海,范俊锴,等.离散单元法软件EDEM中接触半径对岩石力学特性的影响及其应用[J].岩土力学,2022,43(sup1):580 590.
SHEN Haohan,ZHANG Hai,FAN Junkai,et al.Influence of contact radius on rock mechanical property and its application in discrete element method software EDEM[J].Rock and Soil Mechanics,2022,43(sup1):580 590.
[19]CUNDALL P A,STRACK O D L.A discrete numerical model for granular assemblies[J].Géotechnique,1979,29(1):47 65.
[20]贺续文,刘忠,廖彪,等.基于离散元法的节理岩体边坡稳定性分析[J].岩土力学,2011,32(7):2199 2204.
HE Xuwen,LIU Zhong,LIAO Biao,et al.Stability analysis of jointed rock slopes based on discrete element method[J].Rock and Soil Mechanics,2011,32(7):2199 2204.
[21]刘春,乐天呈,施斌,等.颗粒离散元法工程应用的三大问题探讨[J].岩石力学与工程学报,2020,39(6):1142 1152.
LIU Chun,YUE Tiancheng,SHI Bin,et al.Discussion on three major problems of engineering application of the particle discrete element method[J].Chinese Journal of Rock Mechanics and Engineering,2020,39(6):1142 1152.
[22]陈建国,邓金根,袁俊亮,等.页岩储层Ⅰ型和Ⅱ型断裂韧性评价方法研究[J].岩石力学与工程学报,2015,34(6):1101 1105.
CHEN Jianguo,DENG Jingen,YUAN Junliang,et al.Determination of fracture toughness of modes Ⅰ and Ⅱ of shale formation[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(6):1101 1105.
[23]WU Haoyan,KEMENY J,WU Shunchuan.Experimental and numerical investigation of the punch through shear test for mode Ⅱ fracture toughness determination in rock[J].Engineering Fracture Mechanics,2017,184:59 74.
[24]YOON J,JEON S.Experimental verification of a PTS mode Ⅱ test for rock[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(sup1):8 13.
[25]ZHAO Gaofeng.High performance computing and the discrete element model:Opportunity and challenge[M].Oxford:Elsevier,2015.
[26]ZHAO Gaofeng,YIN Qiuyue,RUSSELL A R,et al.On the linear elastic responses of the 2D bonded discrete element model[J].International Journal for Numerical and Analytical Methods in Geomechanics,2019,43(1):166 182.
[27]POTYONDY D O,CUNDALL P A.A bonded particle model for rock[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(8):1329 1364.
[28]WENG M C,LI H H.Relationship between the deformation characteristics and microscopic properties of sandstone explored by the bonded particle model[J].International Journal of Rock Mechanics and Mining Sciences,2012,56:34 43.
[29]袁康,蒋宇静,李亿民,等.基于颗粒离散元法岩石压缩过程破裂机制宏细观研究[J].中南大学学报(自然科学版),2016,47(3):913 922.
YUAN Kang,JIANG Yujing,LI Yimin,et al.Macro micro mechanical research on failure mechanism of rock subjected to compression loading based on DEM[J].Journal of Central South University (Science and Technology),2016,47(3):913 922.
[30]李浩然,杨春和,刘玉刚,等.花岗岩破裂过程中声波与声发射变化特征试验研究[J].岩土工程学报,2014,36(10):1915 1923.
LI Haoran,YANG Chunhe,LIU Yugang,et al.Experimental research on ultrasonic velocity and acoustic emission properties of granite under failure process[J].Chinese Journal of Geotechnical Engineering,2014,36(10):1915 1923.
[31]朱星,刘汉香,胡桔维,等.砂岩破坏声发射临界慢化前兆特征试验研究[J].岩土力学,2022,43(sup1):164 172.
ZHU Xing,LIU Hanxiang,HU Jiewei,et al.Experimental study on precursory characteristics of acoustic emission of sandstone failure based on critical slowing down[J].Rock and Soil Mechanics,2022,43(sup1):164 172.
[32]WATKINS J,LIU K L W.A finite element study of the short beam test specimen under mode Ⅱ loading[J].International Journal of Cement Composites and Lightweight Concrete,1985,7(1):39 47.
[33]楊军辉,雷勇军.垂直界面裂纹应力强度因子的加料有限元分析[J].工程力学,2016,33(2):59 65.
YANG Junhui,LEI Yongjun.The enriched finite element analysis of stress intensity factor for a crack normal to bi material interface[J].Engineering Mechanics,2016,33(2):59 65.
[34]张盛,王龙飞,常旭,等.中心直裂纹半圆盘试样的石灰岩断裂韧度尺寸效应试验研究[J].岩土力学,2019,40(5):1740 1749.
ZHANG Sheng,WANG Longfei,CHANG Xu,et al.Experimental study of size effect of fracture toughness of limestone using the notched semi circular bend samples[J].Rock and Soil Mechanics,2019,40(5):1740 1749.
[35]AYATOLLAHI M R,AKBARDOOST J.Size effects in mode Ⅱ brittle fracture of rocks[J].Engineering Fracture Mechanics,2013,112/113:165 180.

