基于改进A_Star算法的移动机器人动态路径规划

李 杰

(安徽三联学院机械工程学院,合肥 230601)

0 引言

随着机器人各方面能力的不断提高,移动机器人可充当劳动力,助人类完成工作,而路径规划是该领域的一项关键技术[1]。

智能规划算法多种多样,包括模拟退火法[2]、人工势场法[3]、神经网络[4]、蚁群算法[5]、粒子群算法[6]、遗传算法[7]等,其中A_Star算法作为一种智能启发式算法,因其良好的通用性及拓展性被广泛应用于物流运输[8-10]、智能仓库[11]、物联网[12]、航空航天[13]及无人驾驶[14]等领域。A_Star算法也可应用于路径规划问题,并对其进行了大量研究。王忠玉等[15]拓展了A_Star算法的搜索领域,在优化路径、评价函数权重比例方面做出了贡献。李二超[16]等通过改进人工势场法对移动机器人避障轨迹进行了研究,但其避障不适合过多障碍物的复杂环境。而动态窗口法模型简单,局部避障能力强,可以适应复杂环境,但容易陷入局部最优。

根据上述问题,本研究提出一种将改进的A_Star算法与改进的动态窗口法相结合的方式,解决机器人在复杂环境下随机避障问题。从减少搜索方向、平滑规划路径、优化评价函数、障碍物拓展策略及路径形式等方面对A_Star算法进行改进,得出最优路径,为动态窗口法提供全局指引点。动态窗口法在障碍物随机分布的复杂环境下遇到障碍物时,能够及时进行局部避障。该方法既可以规划出全局最优路径,又能够随时避障。

1 环境建模

环境地图的创建选择使用栅格法,将空间地图划分成相等的二进制参数单元格,每个单元格的位置可以用二维坐标及序号表示出来[17]。移动机器人在栅格图中被视为移动粒子,该粒子运动轨迹被视作规划路径。由于栅格的大小会影响算法的搜索速度及结果的准确度,故建立的栅格大小为46节点×46节点。地图上共2116个节点,并做出了以下假设:

1)环境中的静态障碍物是初始化地图随机生成的,动态障碍物是根据测试情况随机添加的。假设静态障碍物与动态障碍物是同时存在的,没有障碍的栅格用白色表示,有障碍的栅格用黑色表示。

2)为了避免障碍物与移动机器人发生碰撞,将静态障碍物与动态障碍物全部进行膨化处理,膨化程度大小为移动机器人半径的大小,忽略障碍物的高度信息。

3)随机添加动态障碍物选择的坐标与对应栅格的坐标存在偏差,按照就近原则,在一定范围内返回栅格所在整数坐标位置,并进行填充标记。

4)移动机器人步长为两个栅格中心点之间的距离,每一步都占满整个栅格,忽略机器人的高度信息。

2 A_Star算法的改进

2.1 A_Star算法原理

A_Star算法是由Hart等在文献[18]中提出的一种智能启发式算法,通过广度优先搜索的Dijkstra与最佳优先搜索的BFS优点的结合,组成一种设计最短路径的算法。在广度搜索算法基础上加入估价函数,对结点的每一个方向进行评估,从中选择消耗代价最低、最容易到达的路径,解决了广度搜索算法每一个节点都要走一遍的缺点,极大地提高了搜索效率。

在A_Star算法中,每一个结点位置的选择都取决于其估价函数f(n),如式(1)所示:

f(n)=g(n)+h(n);h(n)≤h*(n)

(1)

其中,n表示当前所在的节点数,f(n)代表机器人从起始点经过相应节点到达目标点的估计总代价,g(n)代表机器人从起始点到达当前节点所花费的实际代价值,h(n)代表机器人从当前节点到达目标点的估计代价,h*(n)代表机器人从当前节点到达目标点的实际最小代价。

h(n)也叫做启发函数,启发函数h(n)的选取与优化直接影响着节点的搜索与扩展,进而影响算法的速度及精度。要提高算法的精度与速度,就需要对启发函数h(n)进行优化。

A_Star算法的评价函数是由Dijkstra与BFS两种算法结合而成,当g(n)的权重为1、h(n)为0时,为Dijkstra算法,通过遍历所有节点到起始点的距离,找出并记录距离最短的节点,进而找出最短路径。但遍历的节点过多,导致算法运算速度缓慢。当g(n)的权重为0、h(n)为1时,为BFS算法,通过计算当前点节点到目标点的代价,按照代价最小原则向外扩展邻近节点,直到找到目标点。虽然此算法运算速度较快,但很容易找不到目标点,因此分配合适的g(n)与h(n)比例权重,能够使规划的路径更平滑、更短。

A_Star算法的启发函数常用欧几里得距离、切比雪夫距离、曼哈顿距离。究选取欧几里得距离为启发函数代价的计算标准。3种距离的计算如图1所示。

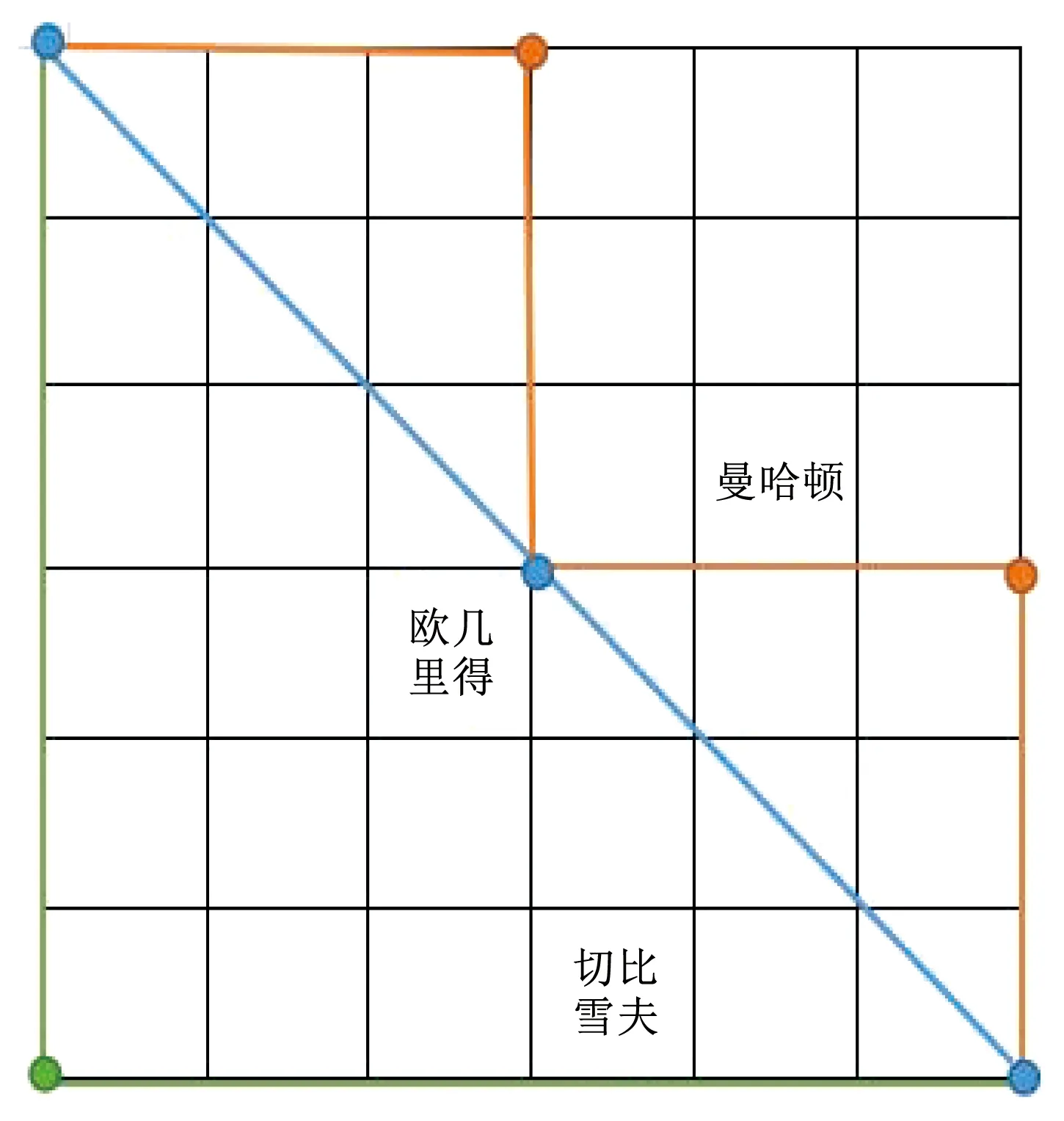
图1 3种距离示意图

2.2 改进A_Star算法

2.2.1 优化A_Star算法的评价函数

A_Star算法的评价函数主要由g(n)与启发函数h(n)组成,其中起主导作用的是启发函数h(n)。当h(n)h*(n)时,搜索的空间变小,搜索节点减少,计算量减少,效率变高,但搜索的路径很难是最优解;当h(n)=h*(n)时,算法运行效率是最高的。当前节点与目标点距离太远、h(n)≪h*(n)时,算法的运算效率很低,为了提高运算效率,应提高权重;反之,随着当前节点与目标点越来越近,h(n)≈h*(n)时,为了防止找不到最优规划路径,由于始终h(n)≤h*(n),故当障碍物较少时,应适当降低启发函数h(n)的权重。综上所述,将A_Star算法的评价函数改进为如式(2)所示:

(2)

其中,r为机器人当前位置到目标点的距离,R为起始点到目标点的距离。

2.2.2 选取最佳关键点

传统的A_Star算法路径规划是由每个栅格的中心点连接而成的。当障碍物增多时,会导致路径的弯折次数增多,使路径不平滑。针对这一缺点,基于Floyd算法思想[19]对路径的弯折问题做出以下优化。

遍历所有节点,删除每一段路径中间存在的多余节点,保留起始点与拐点。

遍历起始点及拐点,从起始点开始将每一个节点与后面的节点相互连接作为可供选择的路径,判断每条路径与障碍物的距离,如果小于安全距离,则舍弃该路径,如果大于安全距离,则保留该路径。

提取连接剩余的节点,作为最优路径输出。

传统的A_Star算法规划路径是以斜线的形式靠近并通过障碍物顶点的,这种情况在真实环境下很容易发生障碍物与机器人的碰撞事件。经过选取最佳关键点改进后,规划出的路径与障碍物保证了一定的安全距离,极大保证了移动机器人在真实环境中的安全。

2.2.3 平滑曲线路径

传统的A_Star算法规划路径是以折线形式连接而成的,机器人在每次转弯处都会出现停顿、再转向、再继续前进的现象。为了使机器人在每次转弯处能平滑运行,在拐弯处以画弧线的方式代替折线进行拐弯,这样转弯时机器人的运动就会相对平滑、连贯。图2是优化前后机器人通过障碍物顶点的对比图。

图2 优化前后对比

2.2.4 优化搜索方向选取策略

传统A_Star算法当前节点到达邻近节点的搜索方向为8个,如图3表示。D代表当前点的位置,D1～D8代表当前节点可移动的8个方向。

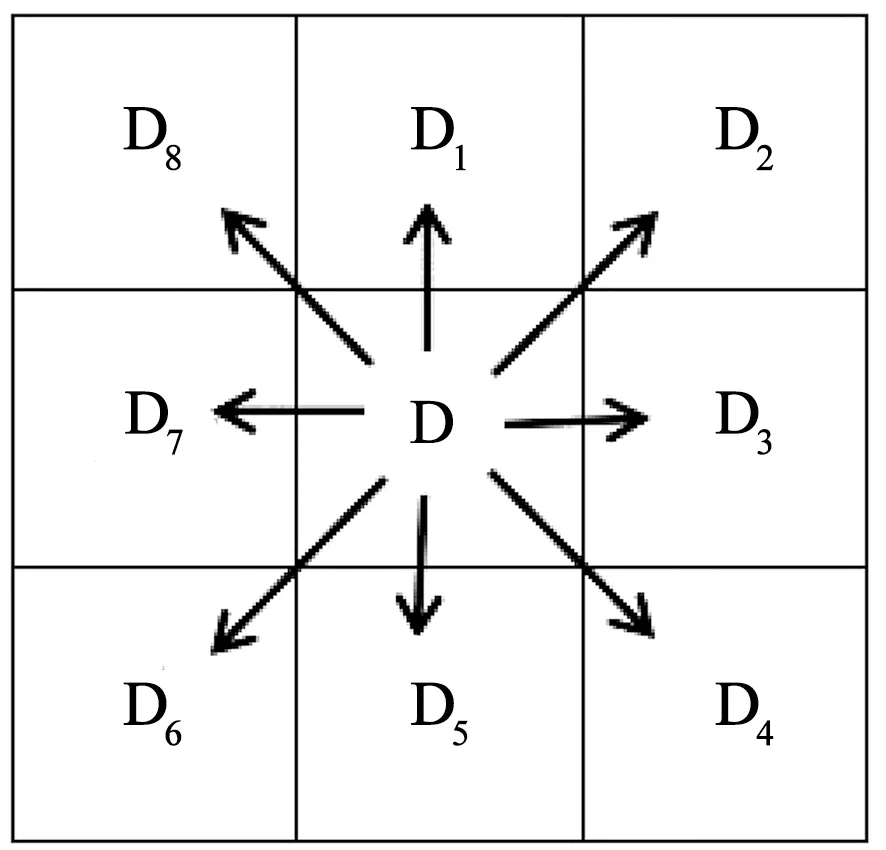
图3 节点移动方向

由于8个搜索方向会增加算法的运算时间,故将搜索方向根据当前节点与目标点的相对方向优化为5个[20],以减少运算,提升算法运行速度及效率。不足之处是当5个搜索方向都存在障碍物时,搜索会陷入死区,无法继续实现路径规划。

将当前节点与目标点的连线与D1的夹角设为α,夹角α与保留的5个方向及舍弃的3个方向之间的对应关系如表1所示。

表1 夹角α与保留的5个方向的对应

3 DWA算法的原理与优化

动态窗口法工作原理是对机器人运动过程中的线速度及角速度进行采样分析,通过速度的数值计算出机器人下一步的运动轨迹,使用评价函数对获得的每条轨迹进行打分评价,从中选出最安全、最平滑的局部最优行驶路线。此时机器人的线速度及角速度为最佳行驶速度。

3.1 动力学模型

假设v(t)与w(t)分别表示Turtlebot2 在世界坐标系下t时刻的线速度及角速度,在采样周期ht内,位移较小,可看做做匀速直线运动[18],则运动学模型的数学表达式

如式(3)表示:

(3)

式中,x(t),y(t),θ(t)分别代表时刻机器人在世界坐标系下的位置姿态。

3.2 速度采样

动态窗口法将避障问题描述为速度空间内带约束的优化问题,根据环境的变换对速度采样的范围进行相应的约束,主要约束机器人的速度、电机加速度及与障碍物的安全距离。

速度约束。移动机器人的速度可以分为线速度与角速度,对速度的约束相当于把线速度与角速度控制在合理的区间内,将其设置为线速度与角速度的集合,DWA算法搜索求解的范围如式(4)所示:

(4)

其中,vmin与vmax分别为移动机器人的最小线速度与最大线速度,wmin与wmax分别为移动机器人的最小角速度与最大角速度。

电机加减速度约束。在对机器人速度进行采样时,要充分考虑电机的性能问题,采样速度单位时间内的变化量应保持在电机最大加减速度规定范围内,其约束条件如式(5)所示:

(5)

其中,admax与aimax为机器人线速度的最大减速度与最大加速度,αdmax与αimax为机器人角速度的最大减速度与最大加速度。vc与wc为当前机器人的线速度与角速度[19]。

对安全距离的约束。为了防止机器人与障碍物发生碰撞,机器人在距离障碍物一定距离时,要满足机器人的线速度与角速度都降为零,其约束条件如式(6)所示:

(6)

其中,admax,αdmax分别为移动机器人的最大减速度与最大加速度,代表预测轨迹末端距离障碍物的距离[11]。

动态窗口算法的速度约束为上述3种速度约束的交集,动态窗口速度可以表示为VW=Vt∩Vs∩Vd。

3.3 评价函数优化与改进

传统的DWA评价函数主要由指向终点的方位角、机器人速度大小、模拟轨迹末端与障碍物的距离3个指标组成。但存在以下不足:由于目标点只有一个,中间缺少指引的临时目标点,在大面积环境中容易陷入局部最优路径。将DWA算法与改进后的A_Star算法相结合,可以提供中间缺少的引导点,极大程度地改善此问题。其未将障碍物进行区分,导致动态避障过程中灵敏度降低[19]。针对此不足,对传统的DWA评价函数进行优化,增加了机器人在动态避障过程中的灵敏度,得出改进后的评价函数如式(7)所示:

G(v,w)=αheading(v,w)+βvel(v,w)

+σpath(v,w)+δdist_1(v,w)+μdist_2(v,w)

(7)

其中,α,β,σ,δ,μ分别为各个子函数的加权系数。heading(v,w)为模拟轨迹终点不断朝向目标点的方向角偏差;vel(v,w)用来评价当前机器人运动速度的大小;path(v,w)用来评价模拟轨迹终点与全局规划路径的距离,使其在局部避障后,能快速回归全局规划路径;dist_1(v,w)用来评价模拟轨迹终点到静态障碍物的最近距离,控制障碍物对局部障碍的干扰;dist_2(v,w)用来评价模拟轨迹终点到动态障碍物的最近距离,通过增加对障碍物的识别能力,提高避障的灵敏度,体现了机器人的避障能力,只有距离大于机器人的半径,模拟轨迹才能通过该评价条件。

4 融合算法

将改进后的A_Star算法与改进后的DWA算法进行融合,主要目的是针对两者算法的优势与不足,达到优势互补的效果。

改进后的A_Star算法虽然在已知障碍物静态环境下能得到全局规划的最优解,但在未知障碍物的环境中无法避障,仅能达到局部的路径规划。DWA算法由于只有一个目标点指引,全程缺少局部方向的指引,当障碍物较多时很容易陷入局部最优,导致无法进行全局的路径规划。

通过两种算法的融合,改进后的A_Star算法能够提取全局规划路径上的关键点为DWA算法作为中间的指引点,在动态环境下为DWA算法提供方向,避免陷入局部最优的状况。优化后的DWA算法也能够对动态障碍物与静态障碍物进行区分,消除一些已知障碍物对路径的干扰,进一步提高算法运算速度。融合算法能够结合两种算法的优点,既具有避障功能,又能规划出最短路径。融合算法的流程如图4所示。

图4 融合算法流程

5 仿真实验

5.1 改进后的A_Star算法仿真实验

仿真实验在MATLAB 2016b环境下进行验证,为了验证算法的适应性及有效性,随机建立了栅格地图,每个栅格设置为面积相等的小正方形,白色栅格代表无障碍区,黑色栅格代表有障碍区。“△”代表机器人的起始点,“○”代表目标点。将改进的A_Star算法、Dijkstra算法、BFS算法进行对比仿真实验,如图5所示。

图5 4种算法仿真实验对比图

5.2 仿真实验结果分析

从仿真图上来看,Dijkstra算法的拐点是最多的、最不平滑的路径,改进的A-Star算法的拐点是最少的,路径是最平滑的。当机器人从一个节点移动到另一个节点的过程中,需要进行原位置转向,转向下一节点方向后再继续前行,故路径过于曲折或过长都会造成机器人能量与时间消耗。由此可以看出,改进的A_Star算法在能量消耗与时间花费上都优于其余3种路径规划算法,便于机器人在实际情况下更好地进行路径规划,到达目标点。

从表2可知,4种不同的路径规划算法最终都能规划出路径,但从各项数据来看还是存在差异的。从计算时间与遍历节点数来看,BFS算法计算时间是最短的,但规划路径是最长的;Dijkstra算法计算时间是最长的,但规划路径是最优的;改进的A_Star算法相比于传统的A_Star,计算时间上平均提高了70%,但路径长度也略微增加了2.4%。改进的A_Star算法性能大幅度优于其他3类算法。

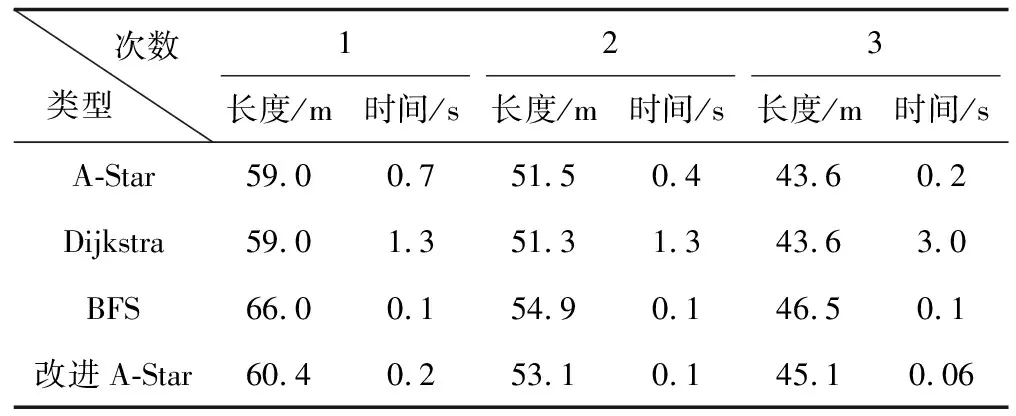
表2 4种路径规划算法性能比较

5.3 融合算法的仿真实验与分析

为了验证融合算法的有效性,在仿真软件中建立了46 m×46 m、栅格间距为1 m的模拟真实场景的栅格地图,进行了1组仿真实验,环境中的静态障碍物覆盖率为30%,随机添加了5组动态障碍物分布在全局规划轨迹附近,目的是最大程度地增加避障难度。实验中,起点坐标为(42 m,45 m),目标点坐标为(11 m,2 m)。实验参数设置如下:最大角速度为15.0 °/s,最大线速度为0.8 m/s,最大角加速度为45.0°/s,最大线加速度为0.25 m/s2。评价函数各项参数如下:α=0.1,β=0.2,σ=0.1,σ=0.05,μ=0.05。融合算法仿真实现过程如图6所示。

图6 融合算法仿真实现过程

从图6可以看出,图6(a)中的虚线为改进后A_Star算法在未添加动态障碍物前所规划的全局路径。图6(b)中方块用来表示全局路径中随机添加的未知障碍物点。图6(c)融合算法路径规划曲线末端的短曲线代表模拟轨迹,路径上的“*”代表提取关键点,作为融合算法的中间引导点。图6(d)代表DWA算法正在绕过了随机添加的动态障碍物,与虚线不吻合的弧线部分代表DWA算法绕过障碍物与全局路径之间的偏差。图6(d)曲线代表机器人在保证规划路径长度最优的基础上使用DWA算法在完美躲避所有障碍物的情况下完成了从起始点到目标点的路径规划。

从最终结果分析,全局静态规划路径的长度为55.87 m,局部动态规划的路径长度为57.32 m,仅仅增加了2.6%。由此可以得出,融合算法既具有避障功能又具有全局最优路径的规划功能,充分地将改进后的A_Star算法与DWA算法的优势相融合。

6 结论

随着机器人领域的蓬勃兴起,路径规划的应用场景越来越广阔,路径规划功能需求也越来越多。传统的A_Star算法存在效率低、路径规划不平滑、只能适应于已知障碍的环境等问题。为了满足实际需求,改进了传统的A_Star算法,利用优先搜索策略将搜索方向从8减少到5,以提高算法的搜索效率。设计了一种路径平滑优化算法,删除多余节点与拐点,提高路径的平滑度,并对自适应函数进行优化,使其随着环境的复杂度变化进行自适应调整,提高了算法的效率及灵活性,加快了收敛速度。通过与Dijkstra算法、DFS算法、传统A_Star算法的对比实验可知,改进后的A_Star算法提高了70%的运算效率。

通过提取改进后的A_Star算法关键点作为DWA算法中间目标点的方式,在全局规划路径最优的基础上实现融合算法。实验结果表明,融合算法规划的全局路径不仅实现了与全局最优路径基本吻合的效果,还能够躲避环境中出现的动态障碍物,进一步提高了路径规划算法的功能,可应用于更多复杂的环境。