在线算法演示虚拟仿真平台开发
——以热传导为例
宋小鹏, 李志伟, 谢云云
(桂林航天工业学院能源与建筑环境学院,广西 桂林 541004)
0 引言
随着信息技术的发展和教学改革工作的推进,当实验操作困难或可视条件不佳时,虚拟仿真技术为教学提供了诸多便利[1-2]。教育部在2020 年发布了虚拟仿真实验教学课程建设指南,旨在更好地应用虚拟仿真技术服务教学工作[3-4]。文献[5-6]中分别利用虚拟仿真技术开展发电厂实习、实践教学,并取得了较好的效果。
传热学中一些常规实验不够直观,无法直接观察到温度场、等温线、热流矢量分布等。田昌[7]针对“传热学”实验开展虚拟仿真教学,探讨和发挥其优势。侴爱辉等[8]探讨传热学实验虚拟仿真和实验结合的教学方式,加强学生对课程内容的直观理解。大量教学工作者,基于Matlab开发传热学实验虚拟仿真[9-11]。Matlab功能齐全,需使用许可,部分高校使用受限。梁秀俊等[12]基于Java 语言,王辉等[13]基于Fluent,李大鹏等[14]基于Energy2D,分别开发了传热学实验虚拟仿真。Java语言、Fluent和Energy2D 等软件具有较高的学习成本,需要较长学习时间,不利于快速入门。
鉴于此,使用Web 前端技术(HTML5/JavaScript)开发算法演示平台,以便对仿真结果进行可视化前处理或后处理。
1 仿真平台的设计与实现
热传导数值求解实验虚拟仿真的常规流程为搭建开发环境(如安装C/C ++ /Fortran 编译器和IDE),程序编制,编译链接和运行,对运行结果后处理、结果分析与程序调试,如图1 所示。为缩短算法演示流程,将实验集中在算法编程的实现上。使用JavaScript 作为编程语言,借助浏览器便能对仿真结果实时可视化。

图1 短流程算法演示
基于Vue-repl、Element plus playground、MathJax和ECharts等开源项目,搭建交互式的实验虚拟仿真平台。Element plus能快速在网页中构建用户界面,提高交互性;MathJax 支持在网页中展示Latex 数学公式;ECharts为数据可视化图表库,可在网页中对仿真结果可视化,如绘制温度曲线或者温度场的Contour 图。仿真平台界面如图2 所示,主要由代码编辑器和计算程序执行结果预览区构成。使用基于vue3.2 的模板(通常包含了用户界面、程序逻辑脚本和样式)编写仿真程序,可对代码关键字进行高亮。当程序修改时,系统可自动编译vue 文件并运行(基于Vue-repl),程序无误时在预览区实时显示仿真结果。
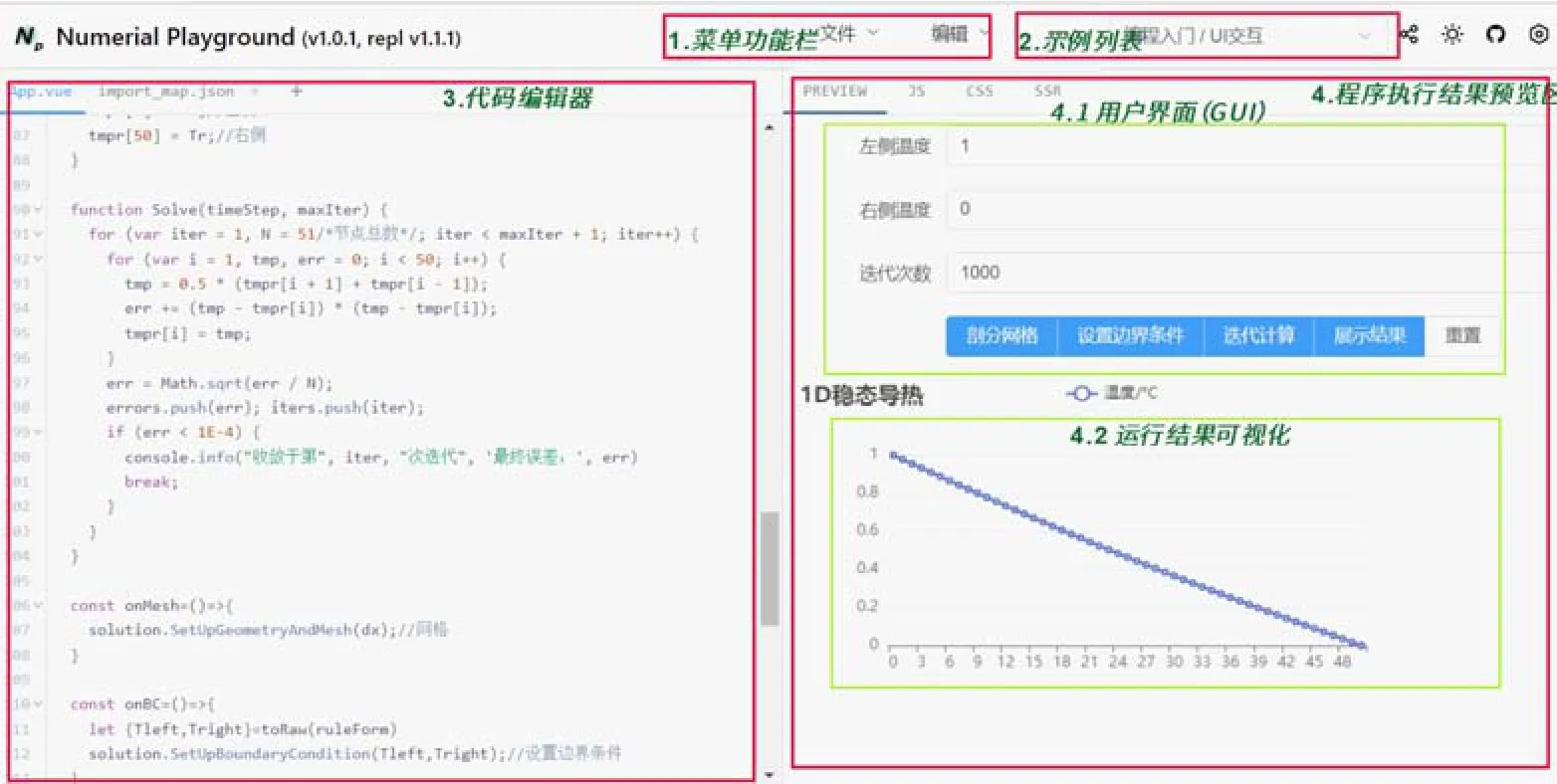
图2 仿真平台界面
用户编辑程序过程中,系统自动检查语法错误,如有错误则显示之,如无语法错误,则对程序进行预览运行,如图3 所示。通常仿真程序运行后,显示用户界面,当用户与页面交互时(如仿真程序的运行参数调整),根据用户输入进行网格剖分、边界条件设置、代数方程的迭代计算以及对结果的可视化展示。仿真程序的运行和数据可视化均在浏览器端进行,服务器端负荷很低。
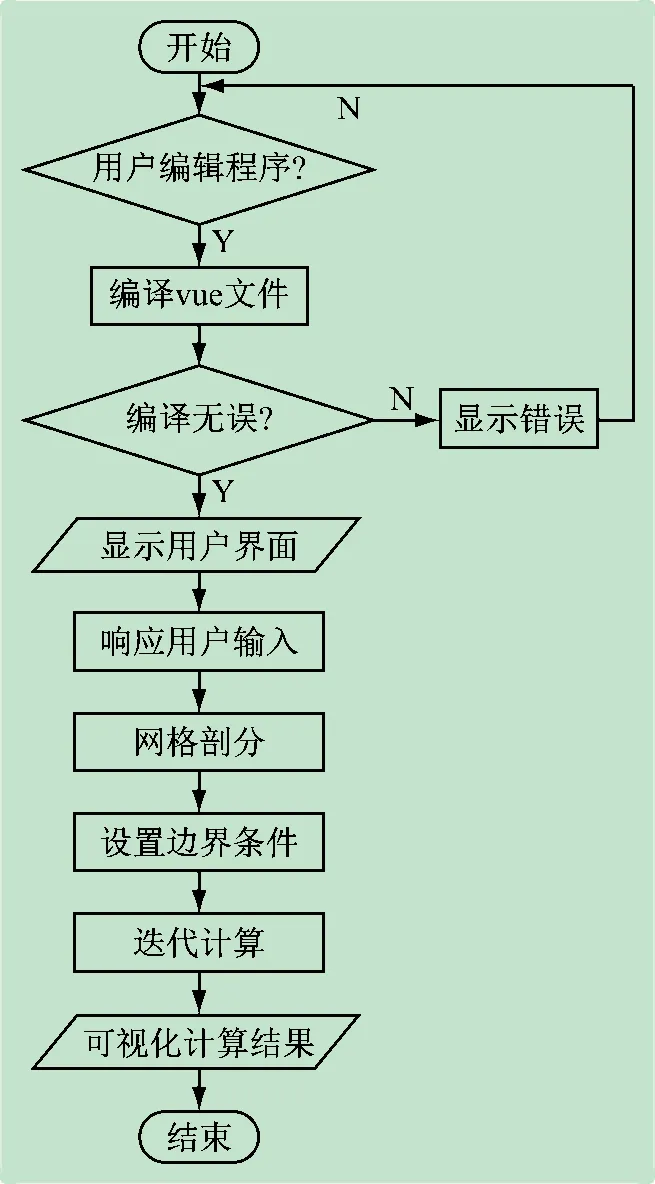
图3 仿真平台程序逻辑
2 热传导实验数值解虚拟仿真算法
传热是典型的扩散传输现象之一,单纯从偏微分方程理解温度场分布较为困难和抽象,将温度场可视化,能直观理解和掌握“场”的概念。基于前述的仿真平台,开发热传导数值仿真程序,将温度场可视化。
2.1 计算域内部节点迭代格式说明
二维矩形计算域的非稳态温度场控制偏微分方程
式中:ρ、CP、λ和T分别为控制体的密度、等压比热、导热系数和温度;为单位体积内热源功率。考虑到控制体内可能有内热源,若内热源功率随节点温度线性变化,则
以规则矩形计算域的正交网格为例,如图4 所示,与节点P直接相邻的有东、南、西、北4 个节点,分别为E、S、W和N,节点P所在控制体大小为Δx·Δy·1(设控制体另一维度为1),节点P所在控制体(形状为6 面体)在东、南、西、北4 个面的面积分别为Se、Ss、Sw和Sn,显然Se=Sw=Δy·1,Sn=Ss=Δx·1。
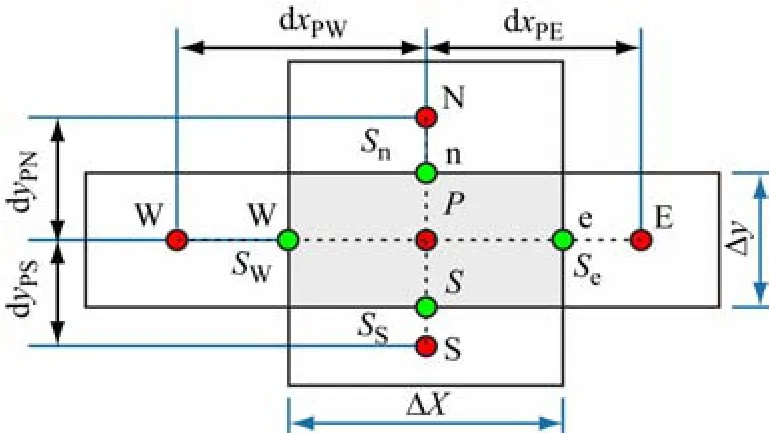
图4 网格及节点控制体示意图
为使迭代计算有明确的物理意义,使用能量平衡法推导面心结构单元的温度场迭代公式。以矩形网格为例,假设计算域内部控制体P仅和与其直接相邻的控制体E、S、W和N 有热量交换,控制体P与四周交换的热量
式中:nb下标为与控制体P直接相邻的4 个控制体;TP为控制体节点P的温度;Tnb为相邻节点的温度;Snb为与控制体P相邻控制体界面的面积。控制体界面上的净传热量与内热源发热量共同决定了控制体内所包含的热量,故控制体温度
式中:V和Δt分别为控制体的体积和时间步长;上标0为上一时刻的值;knb为相邻控制体界面间的传热系数,两相邻控制体换热方式为导热时knb=λnb/dnb,λnb为界面处的导热系数,dnb为节点P到相邻控制体中心点的距离,dnb在东南西北方向上的长度分别为图中的dxPE、dxPW、dyPS和dyPN。特别地,当东西方向网格均匀剖分时Δx=dxPE=dxPW;当南北方向网格均匀剖分时Δy=dyPS=dyPN。如为稳态导热问题,则左侧为0。若各物性参数为常数,网格均匀,稳态导热且无内热源时,可得节点P的显式
2.2 边界节点迭代格式
边界节点的温度求解直接影响整个温度场的求解。第1 类边界条件时,即计算域边界上的节点为已知温度,无须求解。第2 类和第3 类边界条件都可将其等效为源项(内热源),使用“附加源项法”[15]将边界节点作内部节点处理。如图5 所示的边界节点P所在的控制体(阴影部分),有热量输入,并给定边界热流强度为qbound,则对于节点P的热源源项

图5 边界上的控制体有热量传入
显然SC=qbound·Se/V,SP=0。
程序实现时,令P节点东侧传热系数kE=0,P节点内热源相关的系数SC=qbound·Se/V,SP=0 即可。
若边界为第3 类边界条件,给定边界处的对流换热系数α 和环境换热温度Tenv。则对于P节点的热源源项
显然
程序实现时,令P节点的aE=0,内热源相关系数SC=αTenv·Se/V,SP=-αSe/V即可。
对于不规则边界单元,以图6 中边界上的控制体P为例,其东侧和南侧处于边界节点上,东侧为第3 类边界条件(对流换热系数为α,环境温度Tenv),南侧为热流边界条件(热流强度为qs),其中假设Pe 段和Ps段均为绝热边界条件。为简化计算,使计算域边界上节点温度计算仍然可使用内部节点的计算公式,增加实际上并不存在的虚拟节点S 和E,如此边界上的节点可以等效为“内部节点”。处理与控制体S换热的第2 类边界条件时,令该边界上传热系数kS=0,内热源为qsSs/VP,显然此处的换热面积Ss与控制体积VP
均与内部节点不同,需要做特殊处理。处理与控制体E换热的第3 类边界条件时,令该边界上传热系数kE=α,相邻(虚拟)控制体节点温度TE为Tenv。
通过调整节点的传热系数,增加虚拟节点和等效热源的方法,可将边界节点按照内部节点来处理,简化了程序迭代计算。
2.3 仿真结果分析
在矩形计算域0 <x<a,0 <y<b内,求解热物性参数为常数时的二维稳态温度场。设边界条件为=0,根据数学物理方法中的分离变量法,可得其解析解
式中,θ =(2k+1)π/b。若a=50、b=30、A=0.05、B=10,用以上算法和解析解得到绝对误差分布如图7所示。可见计算结果误差较小,表明算法能够求解得到合理数值解。
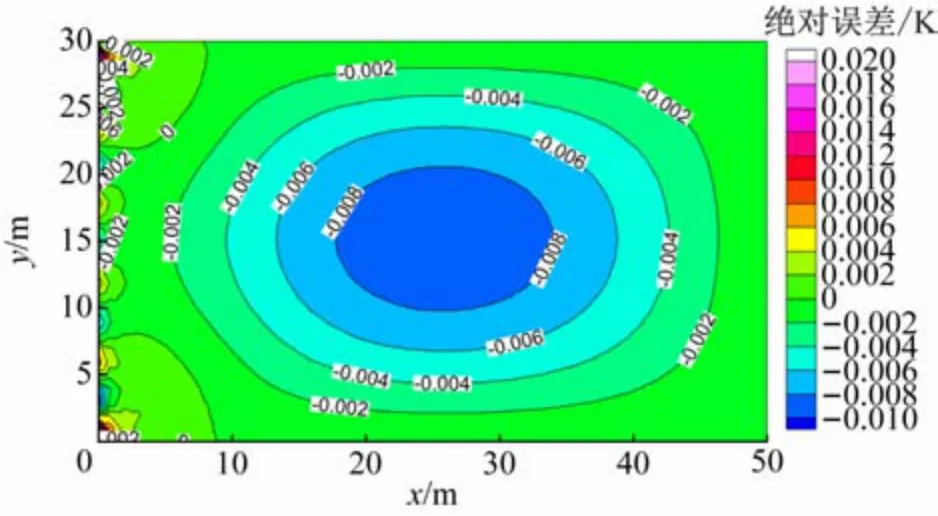
图7 温度场数值解的绝对误差分布
3 热传导实验仿真过程设计
对于算法类虚拟仿真,算法的实现与验证是关键。对首次使用平台或接触JavaScript编程的学生,提供无内热源时的一维稳态导热求解案例。长度为15 个单位的一维物体,两端温度分别为100 ℃和0 ℃。案例设计7 个关键步骤,引导学生了解导热温度场数值求解的基本流程。步骤有:JavaScript 基本语法;用户界面及交互;物理模型与网格剖分[见图8(a)];温度场初始化;边界条件处理[见图8(b)];代数方程迭代求解[见图8(c)];残差计算;计算结果(可参考图2)与残差数据可视化。图8(c)中可见计算结果呈线性分布,说明了算法的合理性。

图8 一维无内热源稳态导热数值解求解过程
经学习一维热传导温度场数值解的案例后,学生已初步掌握了JavaScript编程、数值求解过程及数据可视化等基础知识,基于此,可完成二维稳态温度场数值解求解。其计算条件同2.3,运行界面如图9 所示,左侧为温度场数值求解程序源代码,右侧为温度场Contour图和残差趋势图,其验证已在图7 中完成。核心的稳态温度场计算迭代程序实现仅12 行。残差在100 次迭代时迅速收敛,后期收敛速度较慢。演示页面同样支持手机客户端使用,使实验环境可适用范围更为广泛。
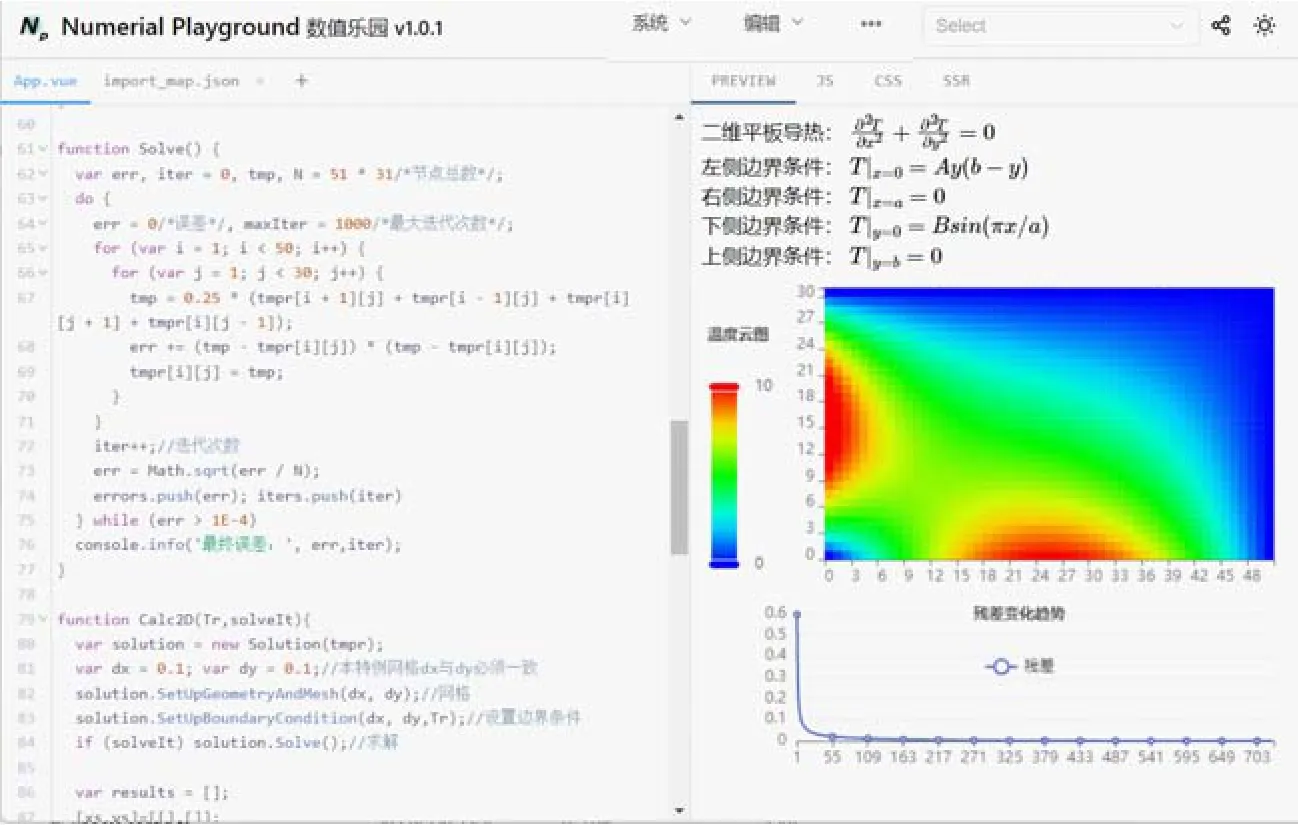
图9 二维无内热源稳态导热的数值求解
4 结语
(1)仿真平台不仅适用于热传导虚拟实验,也适用于常规的算法演示。二维热传导温度场数值解虚拟仿真结果表明JavaScript可用于算法演示。
(2)基于Web 的短流程仿真平台免去了软件安装与开发环境配置环节,能实现脚本程序运行和计算结果可视化,为算法演示类实验虚拟仿真提供了便利。
(3)算法演示类实验虚拟仿真,程序算法的编写和调试至关重要,是理解实验原理和目的关键。
(4)平台基于开源项目构建,支持JavaScript脚本运行、用户界面展示及数据图表的显示,在较简单应用场景中可实现对Matlab一类软件的替代,而不依赖商业软件。

