计算机视觉的桌面型机械臂实验平台设计

金慧萍， 兰天翔， 刘 腾， 于佳琳， 陈 勇

（1.南京林业大学a.工程培训中心；b.机械电子工程学院，南京 210037；2.北京大学现代农业研究院，山东 潍坊 261325）

0 引言

机器人技术涉及运动控制、计算机视觉、人工智能等领域，是当下热门且前沿的研究课题之一［1-2］，机械臂是机器人技术的重要分支，具有重复定位精度高、可靠性强的优点，广泛应用于工业制造、高精密零部件制造、国防等领域［3-4］。随着工业智能化的高速发展，机械臂越来越成为工业生产中不可或缺的工具，且对机械臂的功能有了更高的要求。近年来，许多高校开展了机械臂控制的相关实验研究［5-6］。王倩男等［7］以ROS机器人系统平台为依托，设计了机械臂在线实验系统，可远程控制机械臂，并结合视频监控和实验数据读取来完成相关实验。杨杨等［8］运用Matlab 软件，设计图形用户界面实现机械臂各功能模块的仿真运行，形象地演示机械臂的原理。

随着计算机深度学习技术的发展，机械臂的运动控制开始与机器视觉相结合。杨亮等［9］将视觉伺服添加进机械臂控制系统，通过摄像头采集图像信息，控制机械臂完成目标物体的抓取。郝丽等［10］以Dobot机械臂为主体，设计了视觉辅助的机械臂抓取实验台，可以完成目标物的抓取及搬运任务。当前机械臂控制实验多是基于现有的机械臂本体进行，机械臂系统集成复杂，且造价相对较高，软件开发是在Linux 系统下进行，难于直接上手学习，不利于在实训教学中推广及运用，机械臂功能相对单一，通常只能完成某一种实验功能，不具备二次开发利用的基础。

本文提出一种可用于辅助实训教学的多功能机械臂实验平台设计方案，实验平台采用自主设计的机械臂本体结构，搭载不同的末端执行器，运用计算机视觉技术，摄像头采集到目标物体的图形信息并进行图像处理，转换成运动控制指令通过串口通信传输到机械本体，来实现多功能控制。

1 总体方案

桌面型机械臂实验平台的机械臂本体是1 个三自由度的机械臂结构，分别由3 个舵机控制；控制器由STM32 单片机最小系统板和驱动板组成，上、下位机通过串口通信发送指令实现舵机的运动控制；软件系统基于Python 语言工具开发，运行于Windows 环境下，可实现机械臂的坐标控制、手势控制、示教复演等功能。实验平台原理框图如图1 所示。

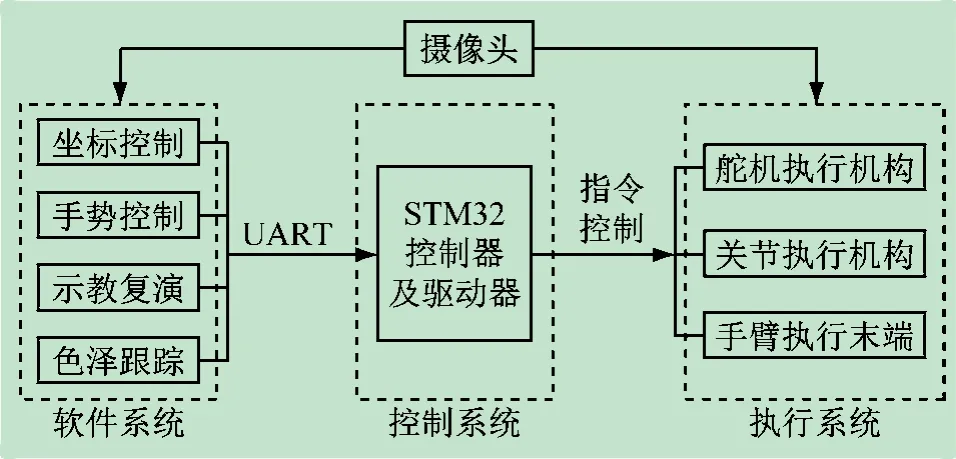
图1 实验平台原理框图

2 结构设计

实验平台的机械本体为关节坐标系结构，共包含4 个关节，分别为腰部结构转动、大臂移动、小臂移动和开放型末端执行器动作。机械臂底座位于实验平台下方，用于固定整个平台系统；腰部结构位于底座上方，可进行周向旋转，实现机械臂整体左转和右转；大臂与腰部结构及小臂相连接，构成一个连杆结构，大臂的移动带动小臂在水平方向上的位移，小臂的移动带动机械臂整体在垂直方向上的位移；机械臂的末端设计了滑槽及销孔结构，末端执行器可根据工作任务的需求进行设计；机械臂结构的零部件采用3D 打印快速成型制造技术加工成型。对机械臂整体而言，以底座坐标系为系统的坐标原点，腰部结构实现左、右旋转，大臂实现前、后移动，小臂实现上、下移动，搭载不同结构类型的末端执行器在腰部结构、大臂及小臂的组合运动驱动下完成具体的操作任务，实验平台的机械臂结构示意图如图2 所示。

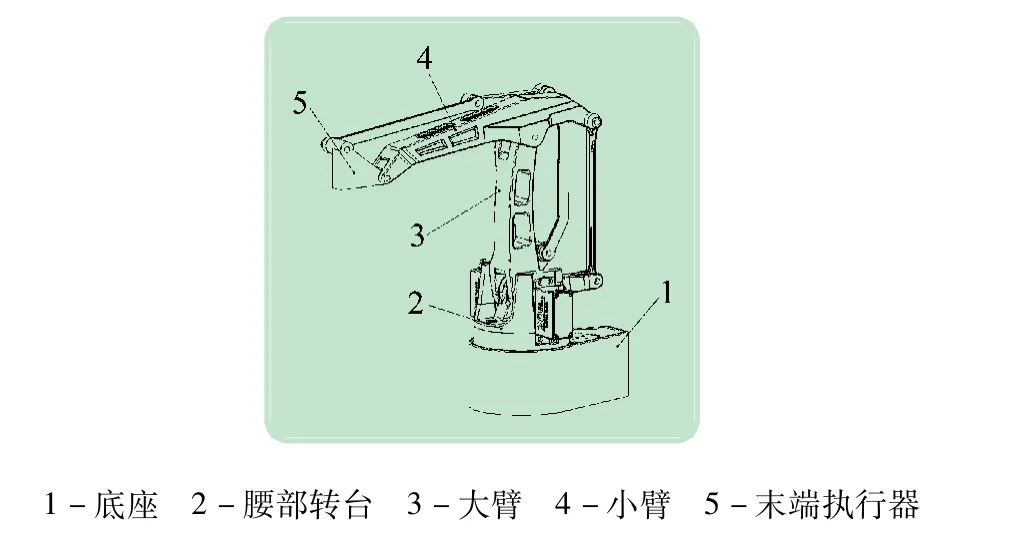
图2 机械臂结构示意图

3 运动学原理

机械臂的运动分析采用Denavit 和Hartenberg 提出的D-H（Denavit- Hartenberg）参数法［11］。在机械臂的每个连杆上固连一个坐标系，以此来描述连杆在空间中的位置状态，通过齐次变换矩阵描述各个坐标系之间的相对关系，从而来表示各连杆之间的相对位姿，在根据各连杆之间的位姿关系建立机械臂的运动学方程，求取机械臂的正逆解。

3.1 机械臂结构参数

图3 所示为机械臂姿态分析图。由图3（a）可知，以机械臂底座为基坐标系O-xyz，J1～J4表示机械臂的4 个运动关节，J2～J4处的轴线相互平行，J1～J3的关节由舵机驱动，J4为被动关节，由J2和J3控制，保持自身姿态为0°。由图3（b）可知，d1为在z轴基坐标系到J1关节公垂线之间的距离；a2，a3分别为J2和J3关节连杆的长度，θ2，θ3分别为J2和J3关节绕z轴的旋转角度。根据D-H 参数法以及机械臂连杆结构简图得到如图3（c）所示的D-H 坐标系，每次坐标系的变换就得到一个转换矩阵，矩阵依次相乘则得到最后的变换矩阵。

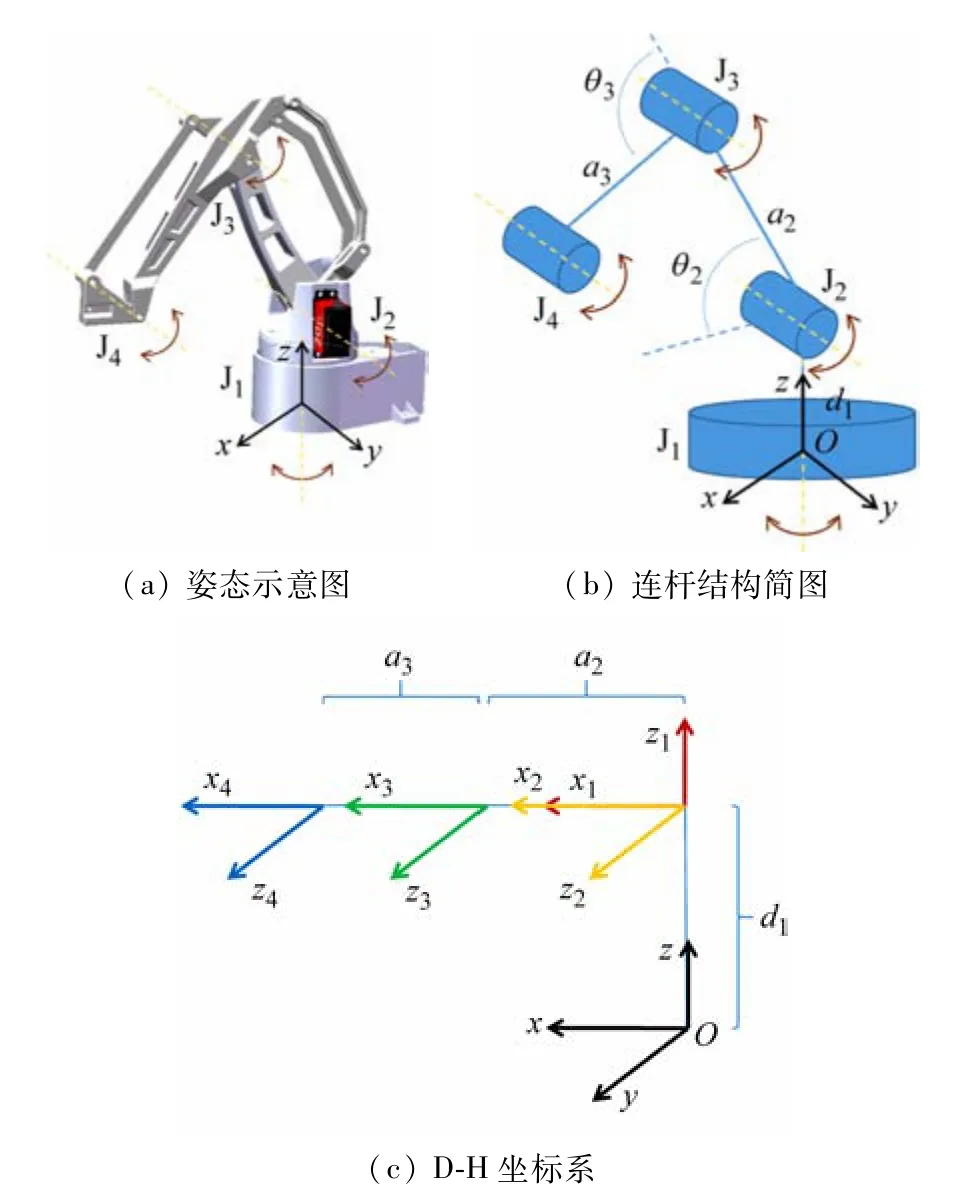
图3 机械臂姿态分析图

根据机械臂的原始尺寸得到D-H模型参数（见表1），其中，i为机械臂各关节序号；α为相邻2 个z轴之间的角度，即关节扭转；a为每一条公垂线的长度，即关节偏移；d为在z轴上相邻2 条公垂线之间的距离；θ为绕z轴的旋转角。

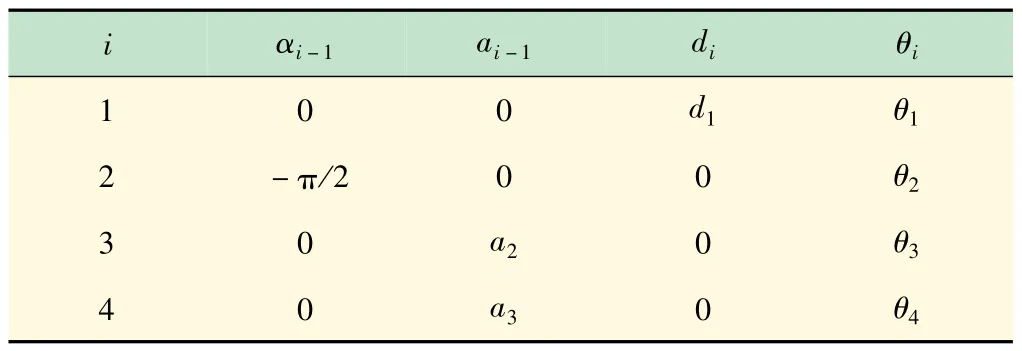
表1 D-H模型参数表

3.2 正运动学分析

机械臂的正向运动学为已知机械臂各个关节参数与变量，求解机械臂末端执行器的位置与姿态的运动分析［12］。机械臂相邻连杆之间坐标系的齐次变换矩阵用i-1Ti表示，其变换通式为

式中：c ＝cos；s ＝sin。

令：C1＝cos θ1，C2＝cos θ2，C3＝cos θ3，C23＝cos（θ2+θ3），S1＝sin θ1，S2＝sin θ2，S3＝sin θ3，S23＝sin（θ2+θ3），根据式（1）可得各坐标系转换矩阵：

求得底座与末端执行器之间的变换矩阵：

当已知机械臂各关节的角度和参数，即可得到机械臂末端执行器的位姿。

3.3 逆运动学分析

逆向运动学是已知机械臂末端执行器的位置与姿态，反向求解机械臂各关节的空间坐标的运动分析［12］。逆向运动学分析方法有解析法、迭代法和几何法等，由于机械臂关节数量较少，本研究采用几何学方法来分析，几何学逆运动学分析如图4 所示。

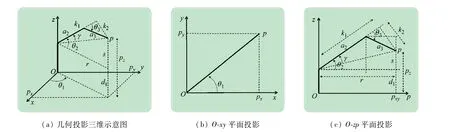
图4 几何学逆运动学分析

机械臂的几何投影三维示意图如4（a）所示，关节末端位置为p点，分别分析机械臂关节在O-xy平面和机械臂所在空间O-zp平面的投影计算出关节的角度值。

（1）O-xy平面投影。由图4（b）可知，由反正切函数得到：

（2）O-zp平面投影。由图4（c）可知，关节2 和点pz形成了1 个三角形，r、s分别为该三角形两直角边，先计算其斜边长，找出获得其他2 个角度值的共同因素，得到：

结合上述几何条件，求解θ3：

沿a2及过点p做辅助线构成直角三角形，其直角边分别为k1、k2，γ为三角形一内角，可得：

进而求得：

至此，得到机械臂逆向运动学方程，由目标位置逆向计算出各关节旋转角度θ1、θ2、θ3的值。

4 平台功能设计

本文应用Python的Tkinter模块进行界面开发，选用Notebook选项卡组件进行布局，可显示多个选项，方便二次开发。开发的实验平台界面包括串口调试、基础控制、手势控制、示教复演界面，将不同的功能界面分别放入不同子组件中，通过类的继承方式进行模块化的程序设计，实现不同界面及功能单独设计的需求，并可以方便地调用已有的功能模块和添加新的功能模块，上位机软件界面如图5 所示。

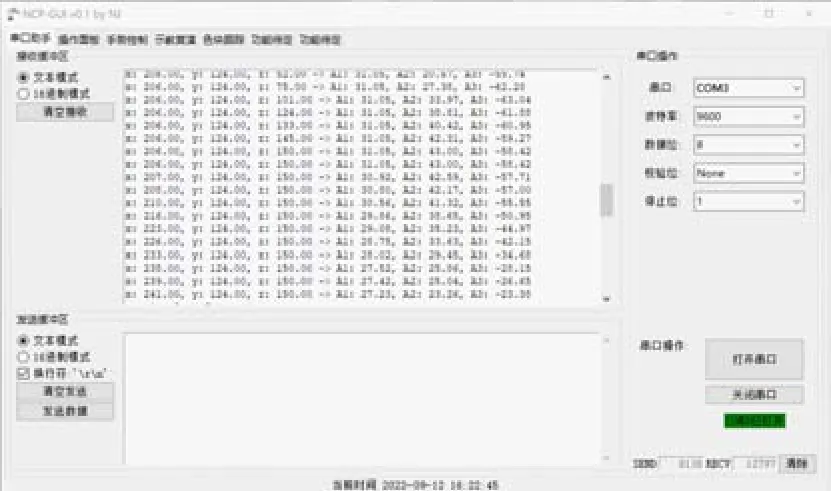
图5 上位机软件界面

（1）坐标控制。坐标控制是对机械臂的基础控制，是实现其他控制功能的前提。上位机向下位机发送相应动作指令，下位机反馈实时状态信息至上位机，打印上位机接收区相应位置供操作者监控机械臂的当前状态。操作面板包括直角坐标控制、关节坐标控制、速度控制功能。直角坐标控制是下位机解析出上位机发送指令中相应的直角坐标参数，通过机械臂逆运动学方程计算出关节角度值，最后控制舵机运动到相应角度，从而实现直角坐标控制；关节坐标控制是系统通过向舵机发送相应脉冲宽度的PWM 信号实现；速度控制是通过改变脉冲发送频率来实现。操作面板界面主要包括直角坐标控制部分、关节坐标控制部分、速度控制部分。在直角坐标控制中加入画布组件，可更加直观的观测机械臂将要运动到的位置，坐标控制界面如图6 所示。

（2）手势控制。手势控制通过捕捉手势图像进行图形处理，手势检测跟踪使用cvzone 模块中HandTrackingModule库实现。捕捉并获取到手指在图像中的坐标后，将该坐标值映射至机械臂的工作空间，获得机械臂运动的目标位置坐标，向下位机发送运动控制指令即可实现手势控制机械臂，手势控制效果如图7 所示。

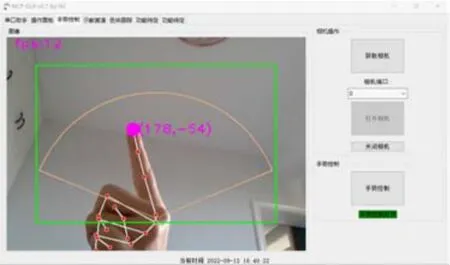
图7 手势控制效果

（3）示教复演。示教复演即可重复再现示教编程存储的作业程序。在设计中，以鼠标在指定的区域运动做示教，机械臂按鼠标的轨迹运动做复演。示教复演界面主要包括图形绘制部分和操作部分，图形绘制部分由画布组件组成，在鼠标按下并拖动时留下鼠标运动的轨迹并记录数据；操作部分由按钮、进度条等组件组成，用于示教复演功能的基础控制。示教界面和演示实验分别如图8、9 所示。

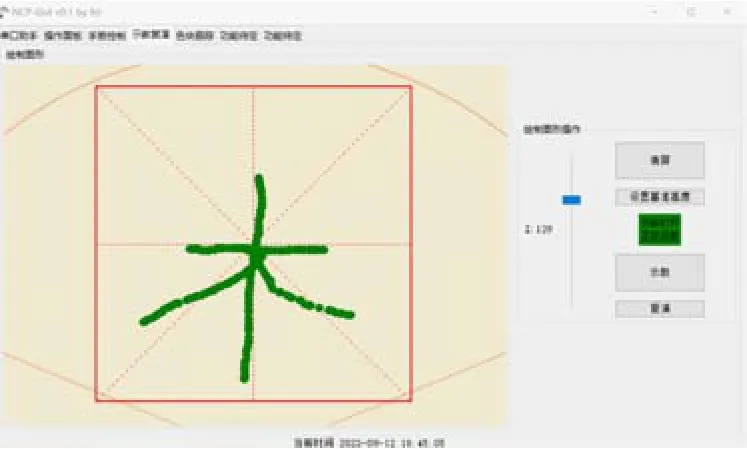
图8 示教界面

图9 演示实验实景

5 结语

本文提出并设计了基于计算机视觉技术的桌面型机械臂实验平台，并通过演示实验进行了测试。结果表明，该实验平台可有效实现机械臂的坐标控制、手势控制及示教复演功能，充分验证了正逆运动学分析的正确性，并可在现有功能上进行二次开发，实现多功能控制目标。该机械臂实验平台采用3D 打印快速成型技术加工制造，具有体积小、加工成本低、联调方便等优点，可应用于“机器人创新实训”课程中，能让学生掌握机械结构设计、电路设计、硬件控制、软件开发等技术的应用，并充分了解学科知识之间的关联性与融合性。