计及风量损耗的油浸风冷外置冷却系统散热效率优化方法

王路伽 蔡镇潞 邱亚博 张乐彬 杨海涛 张建文

计及风量损耗的油浸风冷外置冷却系统散热效率优化方法

王路伽1蔡镇潞1邱亚博1张乐彬1杨海涛2张建文1

（1. 中国矿业大学电气工程学院 徐州 221116 2. 国网安徽省电力公司电力科学研究院 合肥 230601）

为助力变压器冷却系统能效提升，“轻量化、小型化”已成为发展趋势。精确配置风扇直径既能确保高效散热，又能避免造价高、质量重及风损大等问题，与“轻”“小”理念相契合。以往常采用计算流体动力学对冷却系统进行试探性建模与改进，以找出冷却效果显著的配置结构，耗时长且优化目标单一。该文针对油浸风冷（ONAF）模式下散热器构建了一种快速迭代寻优的解析模型，获得了出口油温、油流量及风量分布，在满足既定温差且提升散热效率的同时控制风量损耗。此外，建立了流热仿真与试验相结合的平台，将模型结果与试验、仿真进行对比分析。研究结果表明：风扇直径对油温差的影响呈非线性，风量损耗与直径呈正相关。以PC2600-22/520散热器为验证对象，当风速为3.5 m/s、风扇直径是散热片宽度的1.2～1.5倍时，温差可达到期望值，此时散热效率与风量损耗协同进入最优区间。

轻量化 散热器 风量损耗 油温差 散热效率

0 引言

近年来，为助力变压器冷却系统能效提升，“轻量化、小型化”已成为一种潜在发展趋势，高效合理的散热配置可以有效延长变压器绝缘寿命[1-2]。如何精确地配置风扇直径对冷却系统优化设计至关重要。若选用直径过小的风扇，即只有极小部分散热片散热良好，无法冷却至限定油温；若风扇直径过大，内部油温虽冷却至限定值，但风扇面临造价高、质量重，甚至过多风量浪费等问题。

高效的散热设计是延缓变压器绝缘热老化的重要防线，目前变压器冷却系统的研究主要集中于强化散热性能。有学者验证了水流量、水管材质对水冷散热器冷却性能的影响[3-4]，对于地下变电站这种处于封闭性环境中的变压器，需要采用不同分体式冷却布置方式，可使冷却效率大大提升[5]；M. D. L. Tălu和S. D. L. Tălu指出当调整散热器与本体之间的连接冷却管倾斜角至20°时，其冷却性能得到极大改善[6-7]；Y. J. Kim等设计了多种样式的散热片，在施加相同热源条件下，寻找出冷却性能最佳的换热片形状[8]；D. Susa等提出了基于底层油温的变压器热模型，利用该模型可观察内部绕组散热规律[9]；Z. Radakovic等利用变压器结构、材料物性参数及功率损耗构建了油浸自冷式简化温升模型，可用于变压器冷却设计计算[10]。上述文献皆以散热量最大化来改变变压器系统的结构，尚未综合考虑整体的质量、体积，造成一定的资源浪费，与“轻量化、小型化”设计理念相违背。

研究变压器冷却性能的主要手段是基于计算流体动力学（Computational Fluid Dynamic, CFD）进行试探性建模，挖掘现有冷却结构潜力，通过改变任意段油路结构从局部影响整体油温，有利于提升变压器的散热性能[11]，也有学者利用数值仿真修改油的热性参数，对比废弃植物油与矿物油的散热性能，发现植物油不仅环保，且热点平均温度比矿物油低3 K[12]；外部优化则是通过改变散热器换热片结构或风扇吹气方向和偏移角度使散热效果最大化[13-14]。基于CFD的数值仿真在变压器研究领域的精准性是广泛认同的[15-20]，然而CFD数值仿真虽能获取所需的高精度结果，但等比例三维建模、网格绘制及多物理场模拟等前处理消耗大量计算资源与时间，倘若每次修改特定结构参数，则需反复迭代建模与验证，这意味着CFD仿真需大量试探循环计算，具有一定局限性[21-22]。

综上所述，为了快速、精准地获取变压器散热器的流热特征参数，本文提出一种快速迭代寻优的解析模型，其目的是能够在设计和开发阶段高效、精准地获取油浸风冷（Natural Oil Circulation Forced Air Cooling, ONAF）模式下散热器与风扇耦合热流体动态行为的关键参量，以便于冷却系统结构优化设计。该解析模型中引入了风扇风量泄漏参数，综合考虑风量损耗与油温差之间的动态变化关系，即在满足既定温差且提升散热效率的同时控制风量损耗。所建计算模型被用于求解PC2600-22/520散热器散热片中心处相邻风道的冷却风质量流量与整体油温分布情况，以验证模型的准确性。

1 ONAF散热器计算解析模型

1.1 研究思路

合理控制风量损耗是变压器冷却系统优化设计的重要环节之一。本文对一台油浸风冷式变压器散热器建立计及风量变化关联式的快速迭代寻优解析模型，基于进出口油温差来反映散热效率，改变风扇直径的同时控制风量泄漏值，综合调控风损与温差之间的关系，以此达到冷却系统高效散热的效果。本文设计了一个试验平台来测量变压器冷却系统中不同关键变量的值，例如油流量、散热片之间的空气流速和油温分布情况，作为对解析模型结果验证的依据。此外，还建立了455 mm、655 mm及855 mm三种不同直径风扇下的散热器CFD仿真以验证模型的准确性。本文的研究思路如图1所示。

为了反演ONAF模式下流经散热器通道的油与空气之间的对流传热，提出了基于流体力学和传热学的油浸风冷式变压器散热器物理解析模型，该模型的核心为基于多组耦合的动量和能量微分方程，其中对流传热方式如图2所示。

由于风扇直径不同，风量会有不同程度的沿程损耗与局部损耗，且并非所有散热片都能被风扇作用，一定数量的散热片处于强迫对流状态，剩余的则处于自然对流状态。因此，本文建立的解析方程不仅仅是自然-强迫耦合对流模型各热参数的计算，考虑到风扇直径大小对传热效果的影响，将风量泄漏参数作为附加因子耦合到解析模型中。

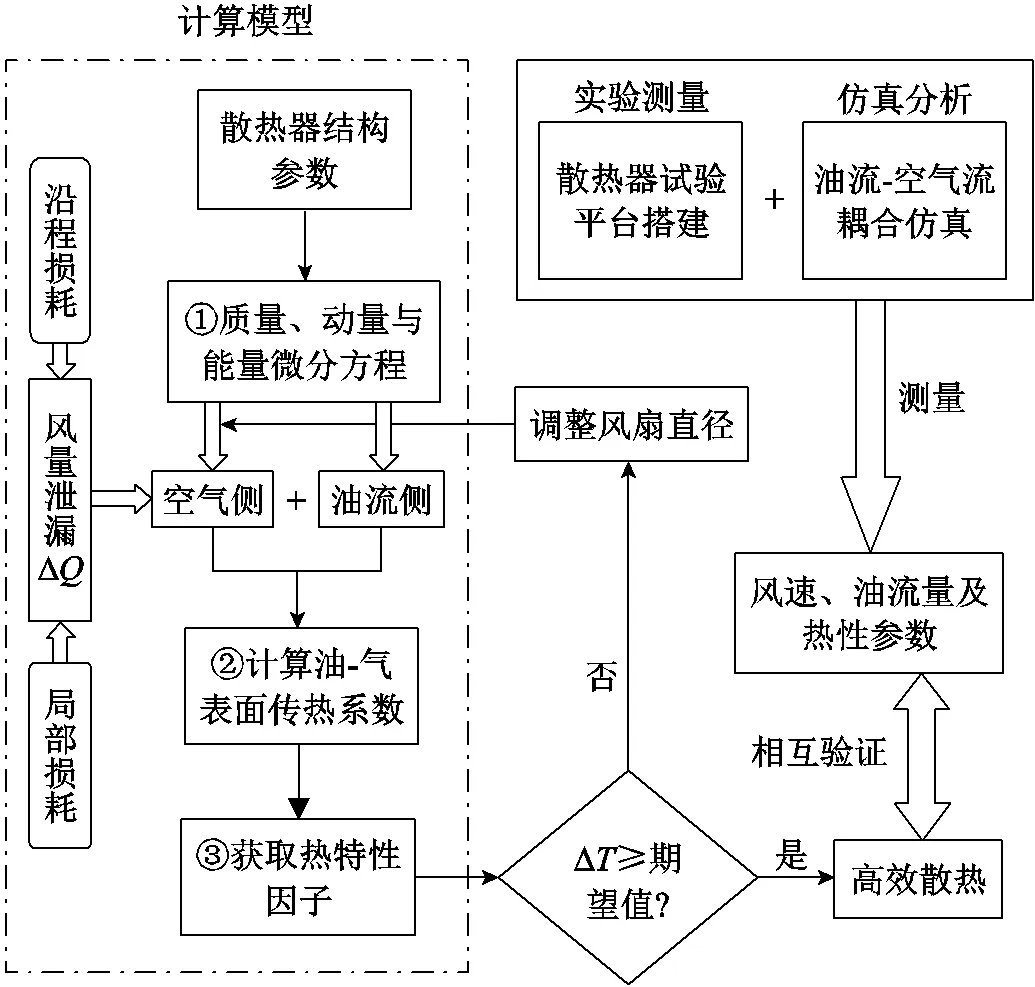
图1 研究思路

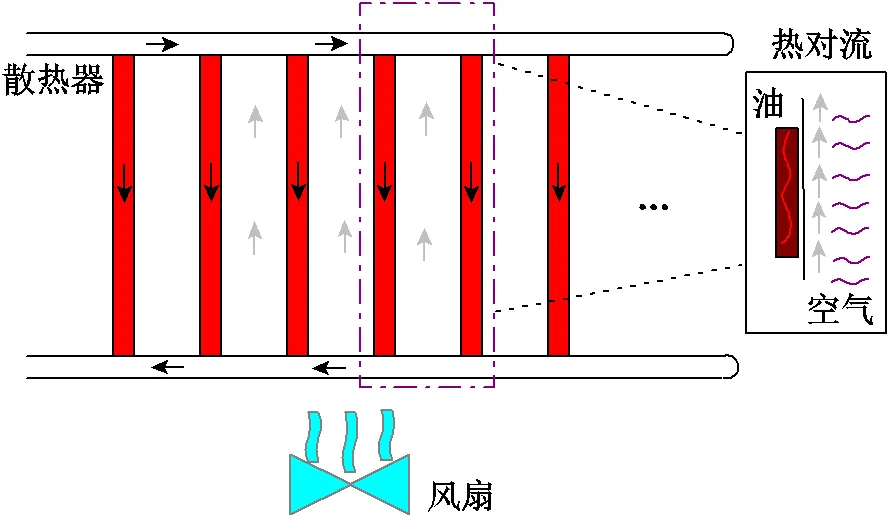
图2 对流传热

1.2 油路侧热特性分析

ONAF模式下内部绝缘油动量与能量守恒，冷却油在绕组与散热器回路之间的流动主要是由热浮升力驱使，影响热浮升力的重要因素之一是绝缘油密度oil，它随着温度呈反比例变化。此外，推动油流循环的热浮升力Δoil与油流流动途中所受到的流阻力相平衡，即

式中，Δoil为散热器入口与出口的油温差；oil为绝缘油的热膨胀系数；为重力加速度；Δ的定义[23]为

其中

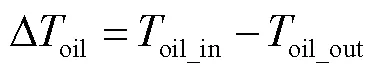
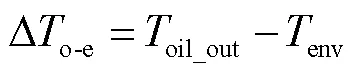
式中，w-r为散热器与绕组中心高度之差；ra为散热器的总高；oil_in和oil_out分别为入口顶层油温和出口油温；env为环境温度；ΔL为散热器内侧油和外侧空气之间的对数平均温差。

考虑到冷却油在散热薄片中的流动，将油流通道简化为宽为oil、长为oil的矩形[24]，则油流量oil计算式[25]为

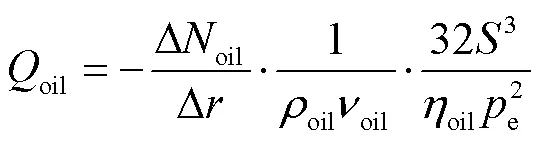
考虑文献[23]提出的油热模型，散热器中油流的传热系数计算式为

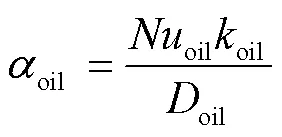
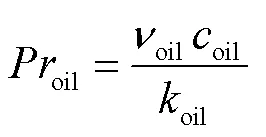
式中，oil为油道的水力直径，oil=4/e；oil为油侧传热系数；∆o-wall为油到散热器壁的温降；oil为油流速；oil为绝缘油的热导率；oil、oil、oil和oil分别为散热片中冷却油的普朗特数、格拉霍夫数、雷诺数和努塞尔数；oil为冷却油的比热容。

变压器运行时铁心与绕组产生的损耗i-w可近似为热能，且热能进行热传导、热辐射与热对流，由能量守恒得出

解析模型中变压器油特性[26]随着温度的变化情况见表1。

表1 油热特性参数集

Tab.1 Oil thermal characteristics parameters

1.3 空气侧热特性分析

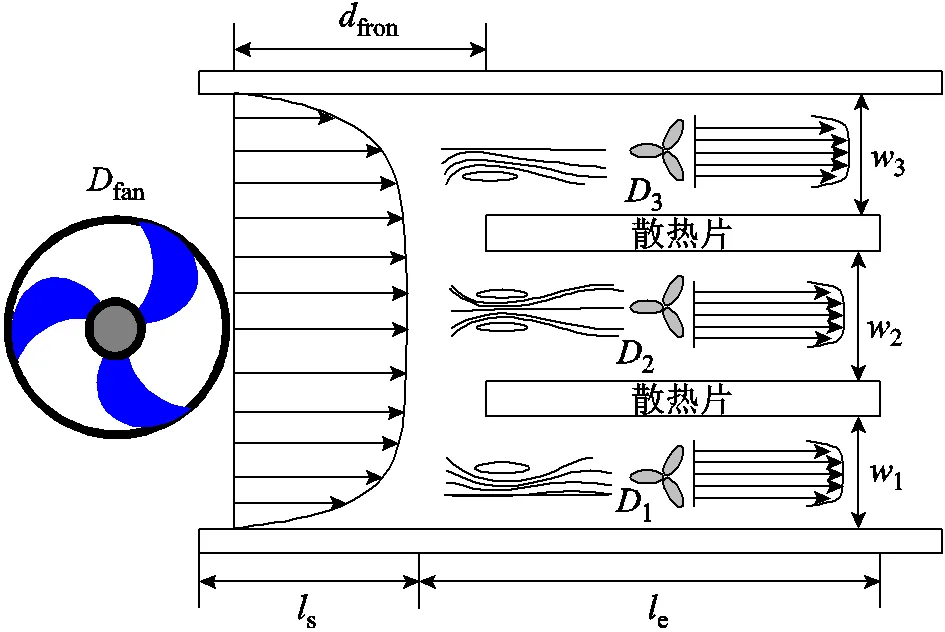
图3 散热器内部风流动示意图

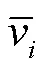
根据流体动力学，冷却风的沿程损耗系数为

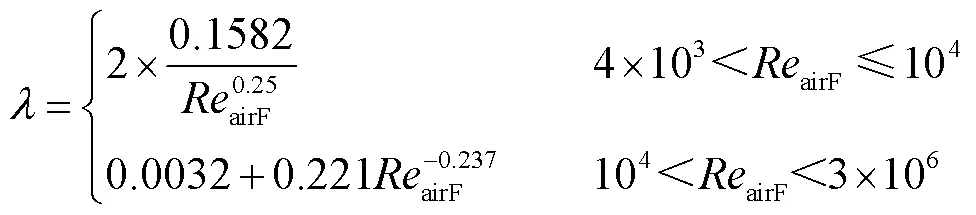
式（12）中，是冷却风流动途中截面积变化产生的局部损耗经验系数，各侧风道局部损耗经验系数求解同风道2。因此，以风道2局部损耗经验系数的求解为例，其计算式为

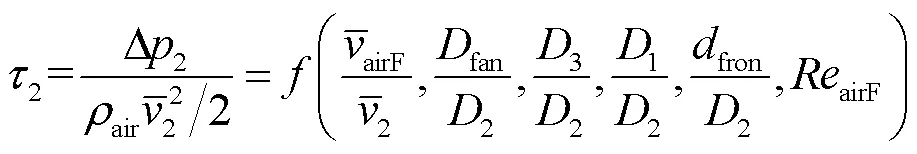
为简化计算，利用无量纲数乘积或商的特性减少参数数量，表示为

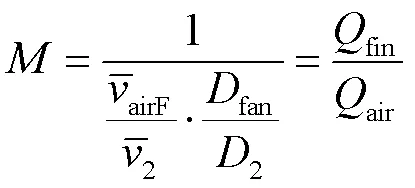
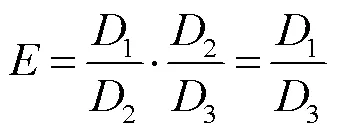
式中，fin为进入散热片中心处相邻风道的冷却风质量流量；air为初始冷却风的总质量流量；为前二者的比值，称为质量流量比；为风道水力直径比，是表征风道几何的无量纲参量。

在流体力学连续性方程及动能方程中引入风扇气动力学附加方程[28]，得到

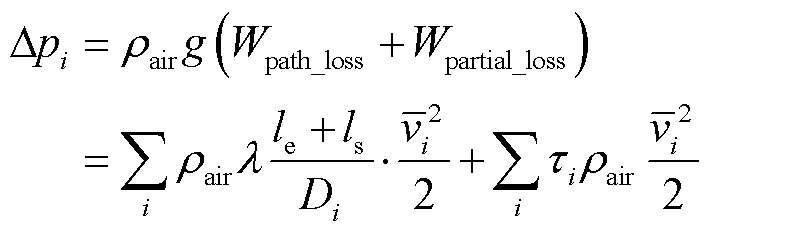
式中，Δp为散热片风道的总压降差；air为风道总高度；air为空气的运动粘度；air为风道面积；为风道周长；air为与空气通道形状有关的经验常数。

1.4 油域-空气域共轭传热

对流传热作为油浸式变压器散热过程中极其重要的方式，与流体流速、密度和温差密切相关。为了评估从油到空气的热传递（oil-air），在分析计算中使用经验方程来预测传热系数。假设每个散热片中的传热方程为

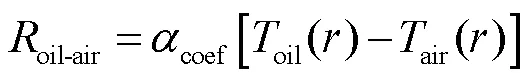
式中，为沿散热片的垂直坐标；coef为总传热系数，包括油、钢铝制成的散热片和空气传热系数。因此，总传热系数可写为

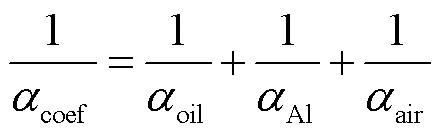
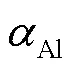
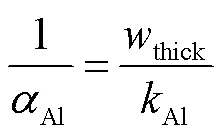
式中，Al为散热片的热导率；thick为散热片的厚度。由于散热器极其不规则的几何结构，thick极小，本文的计算模型中散热方式以对流传热为主。

散热片与空气之间的耦合热传递可以视交界处为垂直平板[29]。空气平均雷诺数airF和平均努塞尔数air表示为[30]

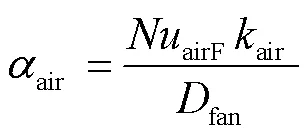
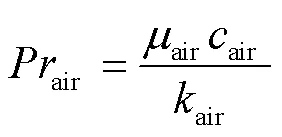
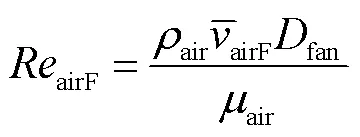
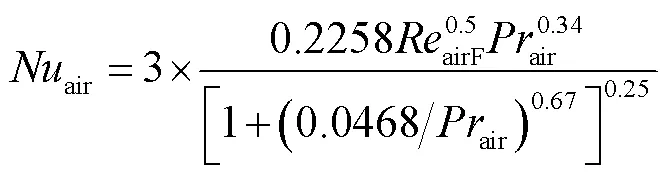
式中，air为空气的普朗特数；oil和air分别为油域与空气域的温度；air为空气的热导率；air为空气的比热容。

自然对流与强迫对流耦合平面图如图4所示。考虑到整个散热器存在混合热对流条件，其中1个散热片是自然对流传热，2个散热片是强迫对流传热，分别如图4中的浅蓝色和浅绿色区域所示。

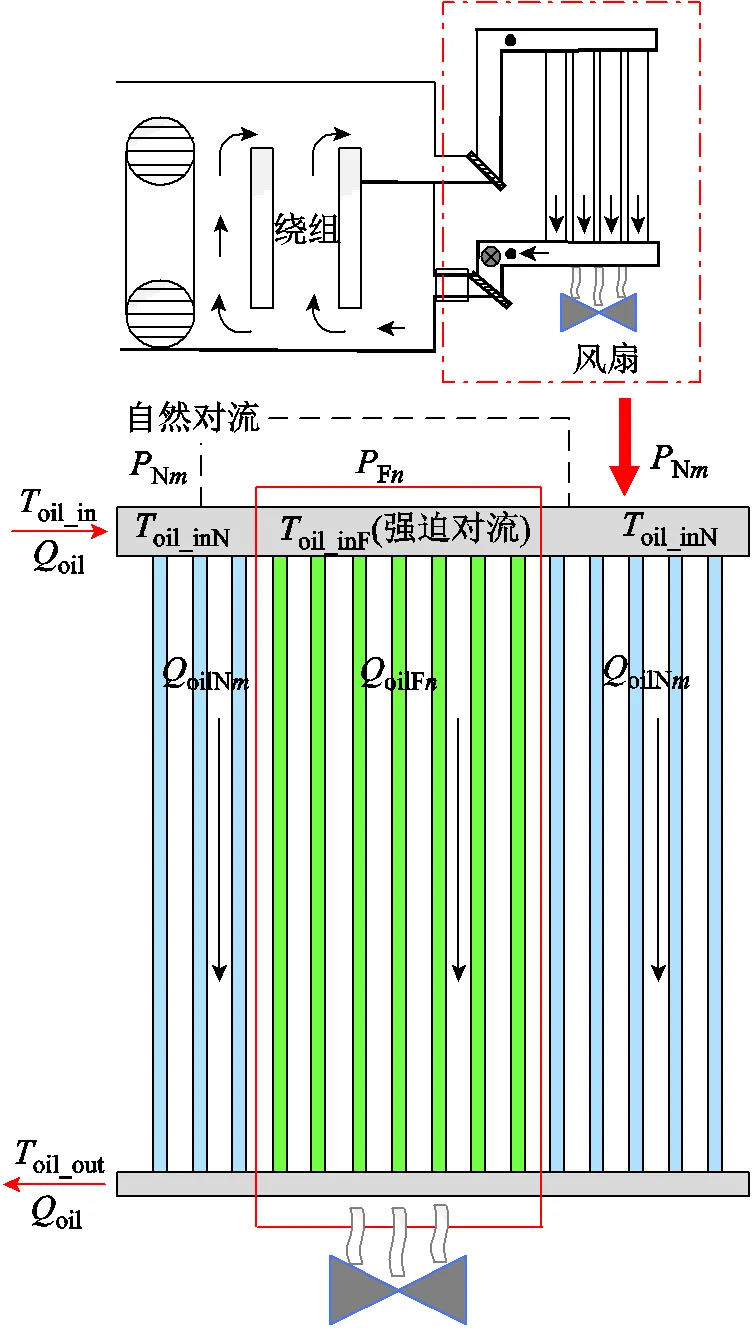
图4 自然对流与强迫对流耦合平面图

总散热功率是自然对流散热量∑Nm（=1, 2,…,1）与强迫对流散热量∑Fn（=1, 2,…,2）之和。假设所有散热片的入口油温与顶层管道的油温一致，各层散热片内部油流量因为热虹吸管力的改变而不同，可得到

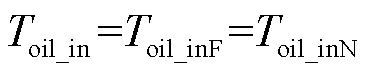
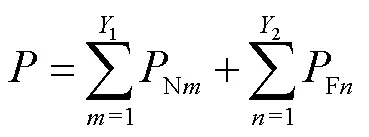
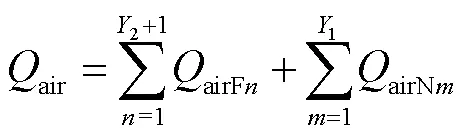
式中，oil_inN和oil_inF分别为自然对流与强迫对流时顶层入口油温；∑oilNm、∑oilFn∑airNm与∑airFn分别为处于自然对流和强迫对流时冷却油质量流量与冷却风质量流量。

出口油温平均值是用自然与强迫耦合对流下的模型计算得出，计算式为

式中，oil_outN和oil_outF分别为自然对流与强迫对流下的散热片出口油温。

通过散热片中的能量平衡微分方程可获得油质量流量与温度分布情况，可表述为

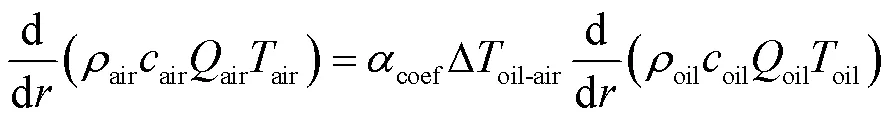
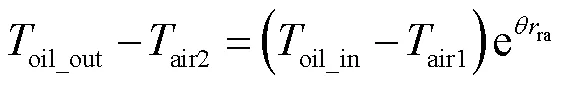
式中，为综合流体物性、传热系数等参数确定的数值；air1为入口空气温度；air2为出口空气温度。解析模型中空气特性随着温度的变化而变化，这些特性参数见表2。

表2 空气热特性参数

Tab.2 Air thermal characteristics parameters

2 模型验证与案例计算

2.1 实验设置与测量

为验证计及风量变化关联式的热工水力解析模型的适用性，首先搭建如图5所示的实验装置。该平台配有1个15 kW的加热装置，1个容积为30 L的油箱和1个散热器。散热器装有22个长为2 600 mm、宽为520 mm、高为50 mm的薄片。风扇安装在散热器底部油管中心下方240 mm处且风速设置为3.5 m/s。同样，使用直径为10 mm的热线风速计来测量散热片之间的空气速度和温度。配置1个7.5 kW的油泵。利用k型热电偶测量位于距底部集管中心200 mm处的油温；利用多个阀门对油路进行调控。选用直径为455 mm、655 mm和855 mm的三种风扇，记录散热器进出口温差变化情况，记录监测的散热器内油流速和出口油温值，并与仿真、计算模型对比分析。

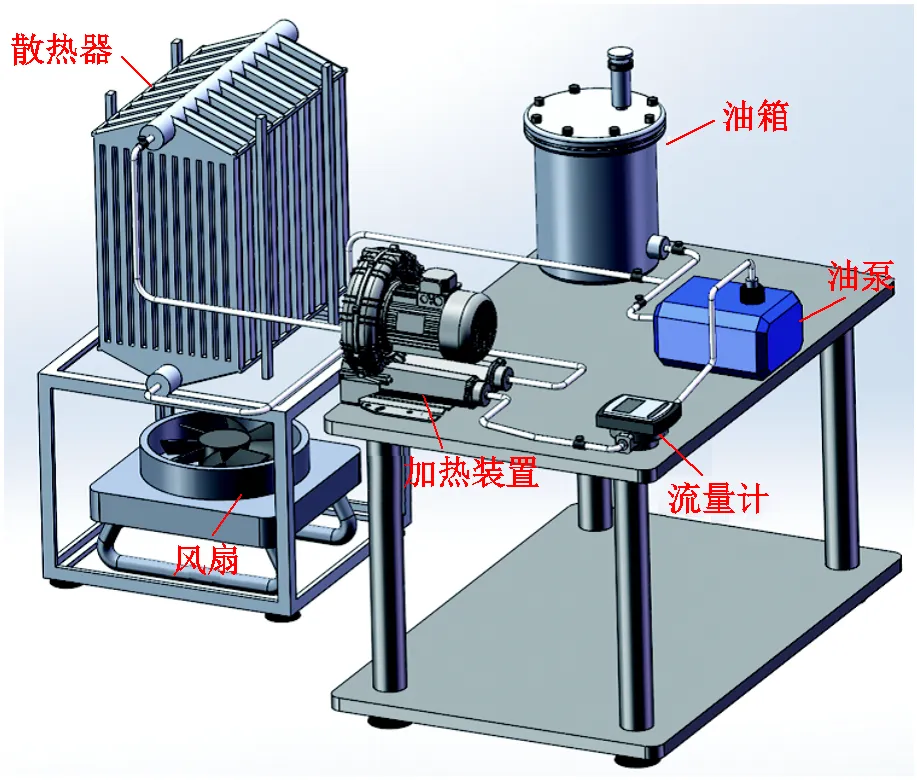
图5 实验装置示意图

2.2 仿真验证

为了使仿真效果逼近实际工况下散热器的散热性能，基于实际应用的散热器尺寸等比例建立三维简化模型。考虑到传热学中的三大传热方式：热辐射、热传导和热对流，建立了长为3.3 m、宽为1.5 m、高为1.7 m的空气域，其中风扇侧所在空气域口被视为入口边界，其湍流强度设置为1%，合理的湍流强度是为了空气被吸入后等效于实际环境。自然油循环空气强迫对流下的三维模型如图6所示，探究455 mm、655 mm、855 mm三种直径的风扇对散热器冷却性能的影响。

图6 ONAF散热器三维模型

2.2.1 网格绘制

本文中，考虑到散热片的高度与长度之比极端失调，采用结构化网格不仅可以减少网格数量，还能保证网格质量与计算精度，因此使用Ansys绘制六面体网格，局部加密网格如图7所示。在简化模型中，风扇可视为二维面，对流体进行离散化，且在流体交界面上需绘制加密边界层。

图7 散热器局部加密网格

设置流体材料如下：两个流体域分别设置油和空气的热物理参数，取油流进口温度为335 K，流速为0.03 m/s，油质量流量为0.3 kg/s，环境参考温度为300 K，强迫对流时风扇入口风速为3.5 m/s，自然对流时空气平均风速为1.05 m/s。此外fluent中连续性、动量、能量的残差分别小于10-3、10-3、10-6，将其作为ONAF模式下散热器对流散热模拟收敛的判别条件。

2.2.2 温度云图与风速流线图

本节探明了ONAF模式下散热器的油流分布规律、进出口油温差及风量分布变化规律。在内部-外部耦合流动与对流传热仿真模拟中，以直径为455 mm风扇作用下的散热器表面与内部温升云图为例，研究了内部油温跃变轨迹与风量流动情况。模拟的散热器温度分布如图8和图9所示。

图8 散热器表面温升云图

图9 散热器内部油流温升云图

散热器内部风道流速与局部风损分布如图10所示，从图中可以看出，受冷却风作用部分的散热薄片内油温明显低于自然对流部分，不同风扇直径下的散热器出口油温有着一定差异。由图10a可知，当风扇直径为455 mm时，风扇作用的区域是在第7～16个散热片；由图10b可知，当直径为655 mm时，风扇的作用范围逐渐扩大至第5～18个散热片；由图10c可知，当直径为855 mm时，风扇的作用区域覆盖第3～20个散热片，三种不同直径下的冷却风分别出现了一定差异性的风量损耗。本文为顺应变压器向“轻量化、小型化”的发展趋势，配置精准的风扇直径，在控制风损的前提下，保证进出口油温差大于18 K。

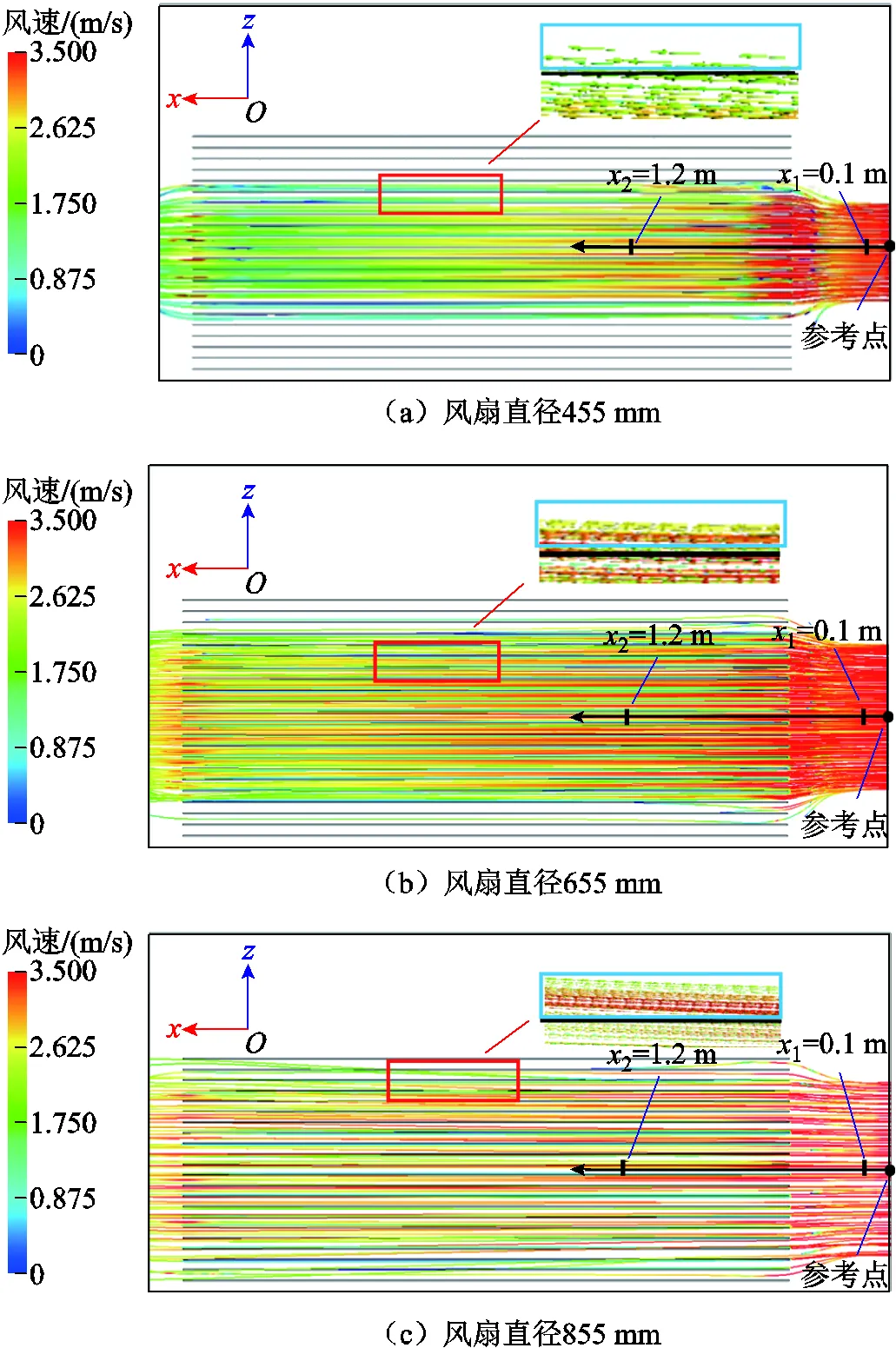
图10 散热器内部风道流速与局部风损分布

散热器风道中冷却风流速从风扇中心（图10中所示参考点）沿着轴正方向有着一定程度的变化。由于风量的沿程损耗与局部损耗，距离风扇越远的散热片传热效果越不理想。空气流速分布如图11所示，以图10中的2=1.2 m处为例，可观察到无论直径取455 mm、655 mm或855 mm，其风速较初始时（图10中1=0.1 m处）的值均有一定的下降。

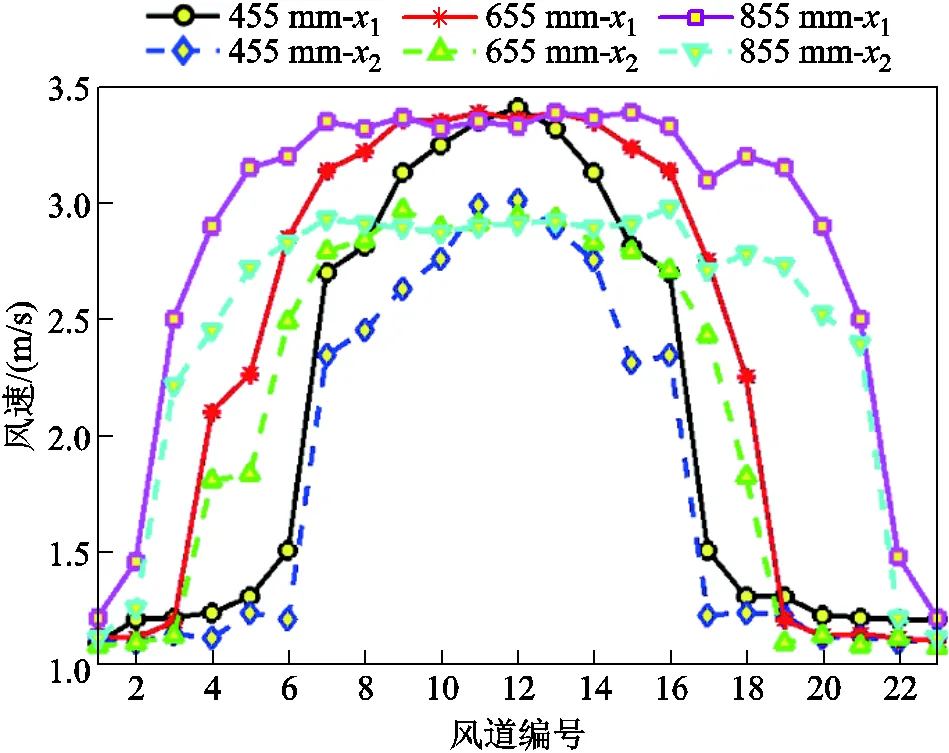
图11 空气流速分布

2.3 案例验证

本文以一台PC2600-22/520变压器散热器为例，具体参数见表3，表4和表5为计算过程中散热片油道与风道的设计参数值。

表3 散热器参数

Tab.3 Radiator parameters

表4 油道参数

Tab.4 Oil duct parameters

表5 风道参数

Tab.5 Air duct parameters

（续）

以配置直径为455 mm风扇的散热器为例，利用第1节模型计算冷却风下散热器流热特征参数，得到结果见表6。

表6 散热器特征参数

Tab.6 Characteristic parameters of heat sink

以CFD仿真及实验测量结果作为计算模型的基准值，沿轴正方向的22个散热片的油质量流量仿真、实验与计算结果的对比如图12所示。从图12可以看出，引入风损的计算模型结果与仿真值、实验值在合理的误差范围内。以直径为655 mm的风扇为例，第11个散热片油流量绝对误差为0.000 9 kg/s；第1个散热片油流量绝对误差为0.003 5 kg/s。在不同直径风扇下，各散热片内油流量分布的变化梯度范围较大，但是总质量流量基本不变。此外，因为始末端散热片与空气充分接触，可以将热量快速辐射到环境中，从而导致热虹吸管压力增大，带来更多的油流量。

沿轴正方向的22个散热片出口油温仿真、实验及计算结果的对比如图13所示，可见强迫对流下散热片油温低，而自然对流下散热片油温高，最外侧两端的散热片油温偏低于其相邻内侧散热片，原因是其与空气接触面最广，传热性能优于内侧散热片。此外，仿真与计算模型是空气域与油域直接对流传热，而实验考虑到固体自身热阻，其出口油温值偏高，即存在一定的合理性误差。对比不同直径风扇下散热器的散热性能，由于风量沿程损耗与局部损耗的影响，直径655 mm与直径855 mm冷却风影响下的平均底层油温绝对误差为1.25 K，而冷却风流量绝对误差高达0.735 kg/s。

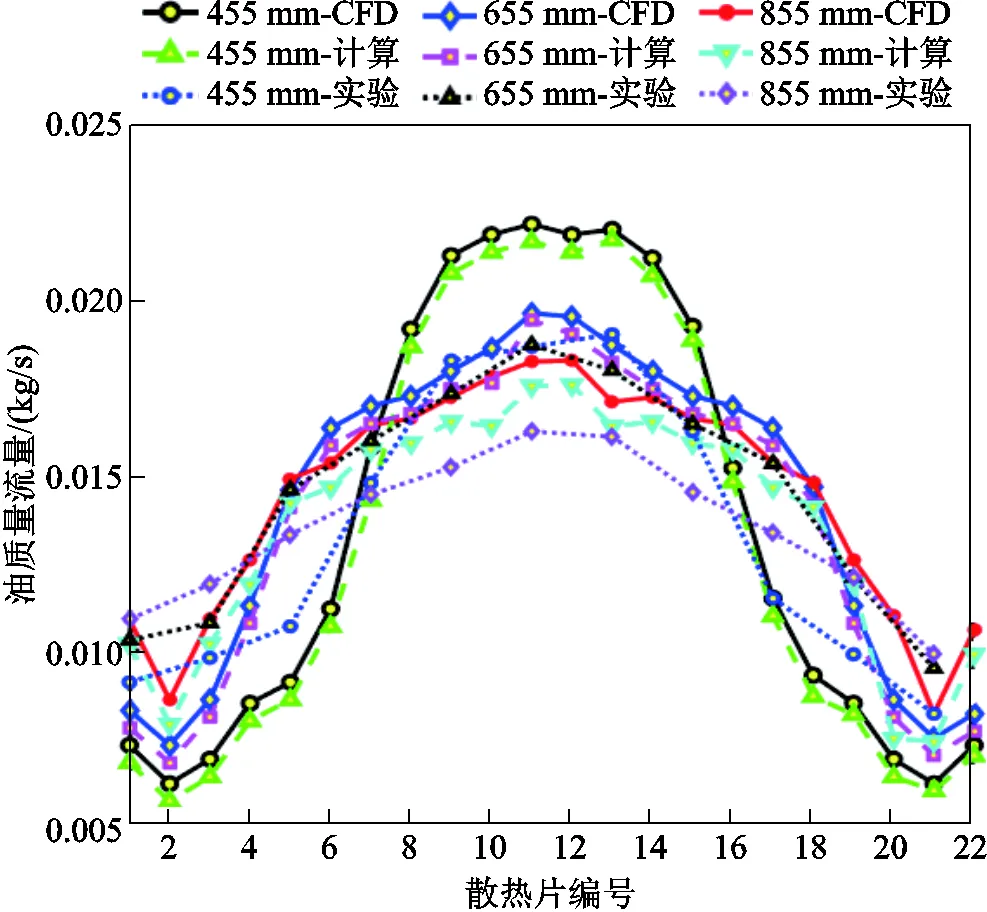
图12 不同风扇直径下油质量流量规律

图13 不同风扇直径下出口油温规律

不同直径风扇下位于散热片中心处相邻风道的冷却风质量流量和底层油温仿真、计算结果及实验测量的误差见表7。由表7可见，整体而言，冷却风质量流量分布的平均绝对误差在0.146～0.231 kg/s之间，平均相对误差均小于6%，此外出口油温的平均绝对误差在5 K以内，平均相对误差均小于1.6%，说明所建计算模型对冷却风质量流量、油质量流量及出口油温的预测结果较为精确。

综上所述，附加风量损耗关联式的热工水力解析模型的正确性得到了较好验证。

表7 解析模型、CFD及实验对比

Tab.7 Computational model, CFD and experimental comparison

3 风损与散热效率协同最优区间

定义散热效率为

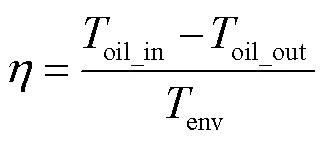
定义温差与风损比为

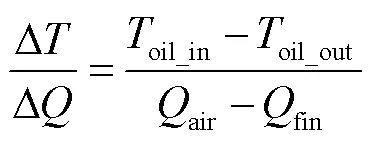
本文探明了油-气耦合流热特性规律，即冷却风作用下的油温差与风扇直径呈非线性关系。图14表示出了风损与温差协同约束下散热效率变化规律，当风扇直径从155 mm扩大至655 mm时，空气侧的风流量增加，散热效率从1.83%升高到了5.5%，提高了3.67%，上升趋势较快；若风扇直径从855 mm持续扩大，即一味追求散热最大化，此时温差变化趋势并未如预期一样快速上升，仅仅是缓慢上涨，风量泄漏参数∆会越来越大，这既增加了系统整体质量，更造成了较大的气动损失。本文的实验测算值、仿真测量值与计算模型结果基本一致，对于PC2600-22/520散热器，设置风速为3.5 m/s，在风扇直径为655 mm时，温差变化趋势放缓，而855 mm之后由于风损值持续增大，致使∆/∆值继续呈下降趋势。此规律表明，当风扇直径为散热片宽度的1.2～1.5倍时，风量损耗控制为最小，且此时进出口油温差达到期望值，散热效率也提升至5.5%～5.75%。所以为了能够真正做到高效冷却，需综合考虑系统整体质量及合理投切风量值。

图14 温差与风损对散热效率的影响

4 结论

本文提出了一种快速高效迭代寻优的解析模型，该模型求解了一组自然和强迫对流散热的耦合非线性方程，考虑风扇气流在散热片之间的分布特性，进行冷却回路的流量和热特性参数的计算，并对散热器散热效率进行了优化提升，得到如下结论：

1）解析方程模型可快速、精准地获取变压器散热器流热特性参数，以案例散热器为例，将总散热量、油温差及风量分布计算总时长由CFD方法的13 h 25 min缩短为7 s，计算效率得到明显提升。

2）散热器解析模型计算所得的风损及温差与仿真、实验结果基本一致，位于散热片中心处相邻风道的冷却风质量流量平均绝对误差为0.146～0.231 kg/s，平均相对误差均小于6%，此外出口油温的平均绝对误差在5 K以内，平均相对误差均小于2%。

3）研究规律表明：风扇直径对油温差的影响呈非线性，风损与直径呈正相关；以PC2600-22/520散热器为验证对象，当风速为3.5 m/s，风扇直径是散热片宽度的1.2～1.5倍时，温差可达到期望值，风损影响控制在最小区域，此时散热效率与温差风损比出现协同最优区间。

[1] 刘丛, 郝建, 李文平, 等. Box-in结构对特高压换流变压器散热性能影响的仿真分析[J]. 电网技术, 2022, 46(2): 803-811. Liu Cong, Hao Jian, Li Wenping, et al. Simulation analysis of box-in structure influence on heat dissipation performance of UHV converter transformer[J]. Power System Technology, 2022, 46(2): 803-811.

[2] Fu Ronghuan, He Zhiguang, Zhang Xing. Life cycle cost based optimization design method for an integrated cooling system with multi-operating modes[J]. Applied Thermal Engineering, 2018, 140: 432-441.

[3] 靳艳娇, 乔光尧, 邓占锋, 等. 全环氧固封高频变压器散热优化设计研究[J]. 电网技术, 2022, 46(7): 2531-2537. Jin Yanjiao, Qiao Guangyao, Deng Zhanfeng, et al. Heat dissipation optimization design of epoxy resin sealing high frequency transformer[J]. Power System Technology, 2022, 46(7): 2531-2537.

[4] 宋全刚, 王琦, 张承, 等. 基于ANSYS分析的水冷散热器多目标优化[J]. 流体机械, 2022, 50(4): 65-70. Song Quangang, Wang Qi, Zhang Cheng, et al. Multi-objective optimization of a water-cooled heatsink based on ANSYS analysis[J]. Fluid Machinery, 2022, 50(4): 65-70.

[5] 魏本刚, 吴楠楠, 任晓明, 等. 基于有限体积法的分体式冷却变压器热学三维仿真技术[J]. 电力自动化设备, 2018, 38(2): 177-181. Wei Bengang, Wu Nannan, Ren Xiaoming, et al. Three dimensional simulation technology of separated cooling type transformer based on finite volume method[J]. Electric Power Automation Equipment, 2018, 38(2): 177-181.

[6] Tălu M D L, Tălu S D L. Modelling of thermal processes of a hydraulic cooling system for a power transformer[J]. The Scientific Bulletin of Valahia University-Materials and Mechanics, 2011, 6(9): 224-227.

[7] Tălu S D L, Tălu M D L. Dimensional optimization of frontal radiators of cooling system for power transformer 630 kVA 20/0.4 kV in terms of maximum heat transfer[J]. University Politehnica of Bucharest Scientific Bulletin Seris C: Electrical Engineering and Computer Science, 2010, 72(4): 249-260.

[8] Kim Y J, Doo J H, Ha M Y, et al. Numerical study on the effect of the shape of the heat transfer plate on the thermal performance of the radiator[J]. Journal of Computational Fluids Engineering, 2015, 20(1): 65-76.

[9] Susa D, Lehtonen M, Nordman H. Dynamic thermal modelling of power transformers[J]. IEEE Transactions on Power Delivery, 2005, 20(1): 197-204.

[10] Radakovic Z, Feser K. A new method for the calculation of the hot-spot temperature in power transformers with ONAN cooling[J]. IEEE Transactions on Power Delivery, 2003, 18(4): 1284-1292.

[11] 徐永明, 刘飞, 齐玉麟. 基于流体网络的电力变压器绕组温度预测[J]. 高电压技术, 2017, 43(5): 1509-1517. Xu Yongming, Liu Fei, Qi Yulin. Prediction of winding temperature in power transformers based on fluid network[J]. High Voltage Engineering, 2017, 43(5): 1509-1517.

[12] Raeisian L, Niazmand H, Ebrahimnia-Bajestan E, et al. Feasibility study of waste vegetable oil as an alternative cooling medium in transformers[J]. Applied Thermal Engineering, 2019, 151: 308-317.

[13] Mahdi M S, Khadom A A, Mahood H B, et al. Effect of fin geometry on natural convection heat transfer in electrical distribution transformer: numerical study and experimental validation[J]. Thermal Science and Engineering Progress, 2019, 14: 100414.

[14] Paramane S B, Joshi K, van der Veken W, et al. CFD study on thermal performance of radiators in a power transformer: effect of blowing direction and offset of fans[J]. IEEE Transactions on Power Delivery, 2014, 29(6): 2596-2604.

[15] 林弘毅, 伍梁, 郭潇, 等. 高功率密度SiC静止无功补偿器强迫风冷散热综合建模及优化设计方法[J]. 电工技术学报, 2021, 36(16): 3446-3456. Lin Hongyi, Wu Liang, Guo Xiao, et al. A comprehensive model of forced air cooling and optimal design method of high power density SiC-static var generator[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3446-3456.

[16] 刘刚, 王晓晗, 马永强, 等. 基于控制体-迎风有限元法的变压器绕组二维流体场-温度场耦合计算方法研究[J]. 高压电器, 2021, 57(6): 1-9. Liu Gang, Wang Xiaohan, Ma Yongqiang, et al. Study on coupled calculation method of two dimensional fluid and temperature field of transformer winding based on control volume-upstream FEM[J]. High Voltage Apparatus, 2021, 57(6): 1-9.

[17] 蒋惠中, 魏本刚, 文杰, 等. 分体式油浸自冷变压器三维温度场和流场仿真与分析[J]. 高压电器, 2021, 57(2): 63-69. Jiang Huizhong, Wei Bengang, Wen Jie, et al. Numerical simulation of 3D temperature and flow fields in separated oil-immersed cooling transformer[J]. High Voltage Apparatus, 2021, 57(2): 63-69.

[18] 王泽忠, 李明洋, 宣梦真, 等. 单相四柱式变压器直流偏磁下的温升试验及仿真分析[J]. 电工技术学报, 2021, 36(5): 1006-1013. Wang Zezhong, Li Mingyang, Xuan Mengzhen, et al. Temperature rise test and simulation of single-phase four-column transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1006-1013.

[19] 唐钊, 刘轩东, 陈铭. 考虑流体动力学的干式变压器热网络模型仿真分析[J]. 电工技术学报, 2022, 37(18): 4777-4787. Tang Zhao, Liu Xuandong, Chen Ming. Simulation analysis of dry-type transformer thermal network model considering fluid dynamics[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4777-4787.

[20] 程书灿, 赵彦普, 张军飞, 等. 电力设备多物理场仿真技术及软件发展现状[J]. 电力系统自动化, 2022, 46(10): 121-137. Cheng Shucan, Zhao Yanpu, Zhang Junfei, et al. State of the art of multiphysics simulation technology and software development for power equipment[J]. Automation of Electric Power Systems, 2022, 46(10): 121-137.

[21] 赵志刚, 张学增. LLC平面变压器绕组损耗与漏感改进有限元计算方法[J]. 电工技术学报, 2022, 37(24): 6204-6215. Zhao Zhigang, Zhang Xuezeng. Improved finite element method of winding loss and leakage inductance for planar transformer used in LLC converter[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6204-6215.

[22] 朱涛, 王丰华. 地磁感应电流作用下大型变压器的温升特性计算[J]. 电工技术学报, 2022, 37(8): 1915-1925. Zhu Tao, Wang Fenghua. Calculation of temperature rise of large transformer under geomagnetically induced current[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 1915-1925.

[23] Karsai K, Kerenyi D, Kiss L. Large power transformers[M]. New York: Elsevier, 1987.

[24] Fay J A. Introduction to fluid mechanics[M]. Cambridge: MIT Press, 1994.

[25] Rodriguez G R, Garelli L, Storti M, et al. Numerical and experimental thermo-fluid dynamic analysis of a power transformer working in ONAN mode[J]. Applied Thermal Engineering, 2017, 112: 1271-1280.

[26] El Wakil N, Chereches N C, Padet J. Numerical study of heat transfer and fluid flow in a power transformer[J]. International Journal of Thermal Sciences, 2006, 45(6): 615-626.

[27] 孔珑. 工程流体力学[M]. 4版. 北京: 中国电力出版社, 2014.

[28] 周利军, 勾小凤, 袁帅, 等. 轻量化车载牵引变压器风道局部损失系数及冷却风分布计算[J]. 中国铁道科学, 2021, 42(6): 152-161. Zhou Lijun, Gou Xiaofeng, Yuan Shuai, et al. Calculation of local loss coefficient and cooling air distribution in air duct of lightweight on-board traction transformer[J]. China Railway Science, 2021, 42(6): 152-161.

[29] Churchill S W, Chu H H S. Correlating equations for laminar and turbulent free convection from a vertical plate[J]. International Journal of Heat and Mass Transfer, 1975, 18(11): 1323-1329.

[30] Churchill S W. A comprehensive correlating equation for forced convection from flat plates[J]. AIChE Journal, 1976, 22(2): 264-268.

Heat Dissipation Efficiency Optimization Method for ONAF External Cooling System Taking into Account Airflow Losses

Wang Lujia1Cai Zhenlu1Qiu Yabo1Zhang Lebin1Yang Haitao2Zhang Jianwen1

（1. School of Electrical Engineering China University of Mining and Technology Xuzhou 221116 China 2. Electric Power Research Institute of State Grid Anhui Electric Power Company Hefei 230601 China）

To help improve the energy efficiency of transformer cooling systems, “lightweight and miniaturization” is a development trend. The precise configuration of the fan diameter ensures efficient heat dissipation and reasonable air volume distribution while avoiding the problems of high cost, heavy mass, and large air loss, which is in line with the “light” and “small” concepts. The main means to study the cooling performance of transformers is often based on computational fluid dynamic (CFD) tentative modeling and improvement, to explore the cooling effect of the configuration structure, but CFD numerical simulation can obtain the required high precision results, but the pre-processing such as equal scale 3D modeling, mesh drawing and multi-physics field simulation consumes a lot of computational resources and time, and the process is complicated and the optimization objective is single. Thus, a fast iterative optimization model is constructed for a radiator with natural oil circulation forced air cooling (ONAF).

Firstly, the analytical model includes the momentum analysis of the overall oil circulation, the cooling air intensity analysis based on the local air loss coefficient, and the heat transfer analysis of the internal oil flow and external air of the radiator. Among them, the momentum analysis of oil circulation is the core of radiator temperature rise calculation, and the local loss coefficient of air volume is closely related to wind speed, fan diameter, cooling air distance, and duct perimeter, and directly affects the Nusselt number (), which is the most important dimensionless number reflecting convective heat transfer strength. Matlab is then used to iteratively calculate the flow-heat characteristic parameters of the analytical model to obtain the radiator import and export oil temperature difference, the relationship between air loss and heat dissipation efficiency is finally integrated and controlled to achieve efficient heat dissipation in the cooling system.

Secondly, to verify the accuracy of the analytical model, a combined flow-thermal simulation and test platform was also established based on the PC2600-22/520 radiator with an equal scale. The k-ε model was selected for the simulation, and the physical parameters of mineral oil, air, and heat sink were defined. In the test, three types of fans with diameters of 455 mm, 655 mm, and 855 mm were used to record the temperature difference between the inlet and outlet of the radiator, and a hot-wire anemometer was used to measure the air velocity and the temperature between the radiator fin.

Finally, the research shows that the fan diameter has a non-linear effect on the oil temperature difference, and the wind loss is positively correlated with the diameter. With the PC2600-22/520 radiator as the verification object, the temperature difference can reach the desired value when the wind speed is 3.5 m/s and the fan diameter is 1.2～1.5 times the width of the radiator fin, at which time the heat dissipation efficiency and the wind loss collaborate to enter the optimal interval. In addition, the average relative error between the model calculated cooling air flow rate of the adjacent air duct at the center of the radiator fin and the test and simulation results is less than 6%, and the average relative error of the outlet oil temperature is less than 2%, which saves more than 98.56% of time cost. The work of this paper provides a new idea for the lightweight design of radiator structure under forced air cooling, cooling efficiency improvement and cooling air intensity distribution calculation.

Lightweight, radiator, wind loss, oil temperature difference, heat dissipation efficiency

10.19595/j.cnki.1000-6753.tces.230091

TM411

国家自然科学基金（52207180）和广东省基础与应用基础研究基金（2021A1515110435）资助项目。

2023-01-19

2023-02-16

王路伽 男，1992年生，讲师，硕士生导师，研究方向为电气设备多物理场建模与状态感知。E-mail：lujia.wang@cumt.edu.cn（通信作者）

蔡镇潞 男，1998年生，硕士研究生，研究方向为变压器散热器热建模与仿真。E-mail：zhenlu_c@cumt.edu.cn

（编辑 李冰）