基于非凸惩罚融合套索模型的电机轴承复合故障诊断

王凡，马军,2※，熊新,2，李祥

（1. 昆明理工大学信息工程与自动化学院，昆明 650500；2. 昆明理工大学云南省人工智能重点实验室，昆明 650500）

0 引言

三相异步电机作为现代农业生产活动中电动力农业机械装置的核心部件之一，常被应用于电动碾米机、榨油机、粉碎机等各类固定作业机械中进行电力驱动，它具有效率高、污染小、噪声低、操作方便等优点，因此被广泛运用于农业工程领域[1-3]。电机内部的滚动轴承在设备运转过程中起着支撑和导向的作用，滚动轴承安装简单使用方便，产生的摩擦力小，能够提高机械的工作效率，轴承的健康状态影响着设备机组的运转性能甚至决定着整个运行过程是否可以正常进行[4]。电机轴承属于旋转机械中的易损零部件，由于运行环境和工况复杂多变，当轴承形成一个故障形态后容易恶化并导致其他位置的故障并发，多种故障信号彼此耦合给检测带来了巨大的困难[5-6]。因此，如何在复合微弱故障相互耦合以及强烈外界噪声的环境下，精确提取微弱故障特征是电机故障诊断领域亟待攻克的难题[7-9]。

信号稀疏表示方法作为一种新兴的信号压缩与重构方法，已成功地应用于旋转机械的故障诊断领域，该方法使一维信号矩阵用尽可能少的原子来构造稀疏字典，在保留特征信息的同时降低信号复杂度，从而使我们简单有效地获取复杂信号中所蕴含的特征信息。但是构建惩罚函数的好坏会影响稀疏结果，若惩罚函数设计的不理想会导致函数在表达过程中失去物理意义，且获得的信号稀疏表示结果容易存在与原有信号脉冲不匹配的问题[10]。为使信号通过稀疏表示方法获得更准确的重构结果，近年来，学者提出了稀疏正则化方法，该方法的核心思想是把原始振动信号与待提取的故障脉冲看作一维矩阵或向量，引入正则化项来对稀疏过程进行约束，增强了模型的泛化能力和鲁棒性，并通过求解稀疏正则化的反问题，近似得到故障脉冲信号[11]。目前，稀疏正则化方法有L0正则、L1正则、L2正则、Lp正则以及全变差正则（total variation，TV）。其中，L0正则可求解x中有多少个非零元素，但此求解方法是NP 难问题（nondeterministic polynomial-hard problem，NP-hard problem）；L1正则表示各个参数的绝对值之和，L1范数不可导且是一个有偏估计，难以对较大的稀疏解实现精确估计[12]；L2正则即欧氏距离，规则化能力强但特征选择能力弱；Lp正则的构。上述稀疏正则化方法在故障诊断领域广泛应用，但仍存在难以优化求解的问题。TV 正则因其目标函数保持强凸性，且求解过程较为简单，为振动信号的稀疏重构提供了新的途径，TV 正则通常指凸惩罚全变分去噪方法（total variation denoising，TVD），最早被应用于图像噪声去除，FIGGUEIREDO等[13]提出构造TVD模型对图像中的噪声进行去除，并利用MM（majorization-minimization，MM）算法求解该模型。LAURENT[14]首次将TVD 应用于一维信号降噪并取得了较好的滤波效果，YOU等[15]为了减弱机械振动信号中背景噪声的干扰并准确提取时频谱中的特征脊线，引入TVD 方法进行降噪处理，数值仿真和实测结果表明该方法较好地增强了复杂信号的时频表示能力；JIANG等[16]提出一种VMD（variational mode decomposition，VMD）和TVD 相结合的方法，利用信噪比选取参数，并证明该方法优于小波阈值去噪算法。虽然上述TVD 方法的目标函数具有严格凸性且可以有效保留边缘特征，但在实际运用过程中易低估稀疏系数、丢失高幅值特征成分并难以选取正则化参数[17]。

为了避免上述问题并有效提高信号特征的提取精度，一些学者提出了 NCTVD（non-convex total variation denoising，NCTVD）非凸正则方法能更准确地估计信号值并增强冲击成分的特征，如LP(p＜1)方法[18]、重赋权L2/L1方法[19]、对数惩罚函数、反正切惩罚函数、极小极大凹惩罚函数等。有学者通过加入新的惩罚函数项来提升NCTVD 模型稀疏分解效果，如LIN等[20]将莫罗增强函数融合至非凸惩罚模型中，增强了轴承微弱故障特征，同时利用包络谱识别故障特征频率；HE等[21]将可调小波基因子与广义极小极大凹函数相结合成功应用于旋转机械的微弱故障诊断；TRIPATHI[22]利用对数惩罚函数构造非凸正则化项，并证明了此方法优于其他惩罚函数项和小波阈值去噪；WANG等[23]利用极小极大凹函数结合小波函数构造非凸小波全变分模型成功提取了滚动轴承的微弱故障特征，并应用于实测健康状态数据，验证了该方法的低误报率。还有学者通过构建新的非凸惩罚模型和改进稀疏系数的求解方法来解决原模型难以诊断复杂微弱故障的问题，如WANG等[24]利用k-稀疏性策略来求解NCTVD 模型中的稀疏参数，通过仿真实验和实际测试证明了该方法可以显著提高轴承故障信号的估计精度，HE等[25]将观测到的噪声信号建模为两个重复群稀疏分量与高斯白噪声的和，并采用非凸正则化重复瞬态提取算法对机车轴承的复合故障进行诊断；LI等[26]提出交替方向乘子算法与二分量稀疏低秩矩阵分离方法，对减速机齿轮箱复合故障进行诊断；HUANG等[27]将稀疏表示和傅里叶变换融合构成一个紧凑框架，避免了高维逆矩阵的计算，之后通过分割增广拉格朗日收缩算法迭代求解得到两种混合分量的稀疏系数，从而有效地从齿轮箱振动信号提取出复合故障瞬态成分。

虽然上述非凸惩罚稀疏正则化方法例如反正切惩罚函数模型[28]（arctan non-convex total variation denoising）在故障诊断方面取得了良好的效果，但是在实际应用于电机轴承复合故障诊断时仍然存在着如下问题：稀疏后的数据原子复杂度较大，模型稀疏性能较差；不能充分反映信号的稀疏特征成分，无法提取复合故障特征。

基于此，本文提出基于NCFLM（non-convex fused lasso model，NCFLM）的电机轴承复合故障诊断方法，核心思想是将构造融合套索模型的思想应用到基于arctan 非凸惩罚函数的NCTVD 模型中，构建对L0范数逼近程度高且能保持较高稀疏性的信号分解模型，针对复合故障的振动信号需准确分离的工程需求，引入具有良好保幅值能力的GMC（generalized minimax concave，GMC）函数优化稀疏惩罚函数项，在使模型保持强凸性状态的正则化参数和凸性参数取值范围内，进一步利用遍历寻参方法确认最优的参数组合，并通过试验验证该模型对电机复合故障诊断的有效性。

1 基于TVD 改进的NCFLM 模型

1.1 TVD 的基本原理

全变分去噪模型包含保真项和凸正则化项，可实现对原始信号的稀疏表示。定义一维信号为x(n)(0≤n≤N-1)，n为信号中的第n个原子，N为信号长度，该信号的一阶全变分为

式中Dx表示一阶微分，||·||p（p≥1）为Lp范数，p表示阶数，其中矩阵D的定义如下：

三对角矩阵DDT表示为

且||x||p为

当p=1 或者p=2 时，一阶和二阶范数分别定义如下：

信号x(n)加入高斯白噪声w(n)，可得到合成的原始噪声信号y(n)：

定义全变分去噪模型的目标函数为

式中‖y-表示信号保真项，λ‖Dx‖1表示正则化项，λ为正则化参数，TVD 的目的是找到信号x从而最小化目标函数：

采用MM 算法对式（9）进行求解，以xk+1表示F(x)经MM 算法而产生的第k+1个子序列，diag 表示对角矩阵，求解方程如下：

式（10）迭代求解后得到经TVD 模型处理的重构信号，但通过比较式（8）可以发现正则化参数λ调控着正则化项的惩罚程度：λ越小，惩罚程度越小，重构信号x可能会更接近原始信号y，从而失去稀疏表示的意义；λ越大，惩罚程度越大，当λ大于某个阈值后可能会使信号失真。

1.2 NCTVD 与NCFLM 的基本原理

式（8）中正则化项本质上是L1范数，L1范数在凸函数中有效地增强了稀疏性，但作为惩罚函数的L1范数往往低估了较大的信号值。在诱导信号的稀疏性和估计信号值方面，非凸惩罚函数通常优于L1范数，将λ‖Dx‖1变为非凸正则化项形式，式（8）转化为

式中ϕ表示参数化非凸惩罚函数，正则化项用反正切惩罚函数（arctangent penalty，arctan）来表示，即可得到arctan-NCTVD 模型：

式中参数a控制模型的凸性程度，一般来说，非凸惩罚函数项还包括对数惩罚函数项（logarithmic penalty，log）和一阶有理惩罚函数项（first order rational penalty，rat）如下所示：

SELESNICK 利用MC 非凸惩罚函数和线性最小二乘Huber 函数推导出GMC 非凸惩罚函数，该模型能更精确地估计稀疏解的高振幅分量和诱导稀疏性[29]。本文以文献[28]中的arctan-NCTVD 模型为原始模型，融合GMC 函数对模型进行套索化处理，此步骤的GMC 是由卷积下定义的Huber 泛化推导得到，设一元Huber 函数s(x)的表达式为

设b为压缩尺度变量，若b=0，则s(x)=0；若b≠0，则尺度Huber 函数sb(x)为

设A,B∈RM×N，A、B、R为实数矩阵，v表示靠近x两侧邻域内的点，M和N为矩阵行数和列数，对式（17）进行变尺度处理，将其转化为变尺度Huber 函数sB(x)，表示为

利用式（18）定义的sB(x)进行泛化推导得到GMC惩罚函数PB(x)为

融合套索模型是非凸惩罚模型的扩展，将式（12）按式（20）的形式拓展后并代入式（19），此稀疏优化问题可转化为如式（21）的鞍点近似求解问题，此问题可通过FBA 算法求解，该算法具体步骤见文献[29]，其中 β为数据原子，(xopt,vopt)为迭代处理后得到的鞍点坐标，严格凸函数的参数取值范围如图1 所示，可以看出，参数需在三角形内部取值才能保证模型为严格凸。NCFLM 与常规非凸惩罚模型的区别在于它同时对信号数据原子本身及其差分的绝对值之和进行惩罚控制，减少了具有相同特征邻近原子之间的差值，并统筹兼顾了所有原子的顺序联系性，使得不同特征成分更容易区分。也可以说，融合套索模型处理后的原子不仅是稀疏的，原子之间的连续性差异也是稀疏的，因此在原子和连续性差异之间产生稀疏解，更能促进模型的稀疏性。

图1 强凸函数的参数取值范围Fig.1 Value range of parameters for strong convex function

1.3 NCFLM 与其他非凸惩罚函数的函数值变化曲线分析

为验证本文模型在重构性能方面比常规非凸惩罚函数更具优势，将NCFLM 模型与初始L1范数模型、log模型、rat 模型、arctan 模型的函数值变化曲线进行对比分析。

图2a 为不同惩罚因子的惩罚函数值对比，L0范数虽稀疏特征明显但因其较难优化求解而被称为NP 难问题，L1范数被称为L0的最优凸近似并且比其更容易优化求解而得到了广泛应用，log、rat 以及arctan 非凸惩罚因子作为L1范数的改进，比L1范数更能实现对L0范数的逼近，以x=3 为例，R1、R2、R3、R4、R5的惩罚函数值与R0分别相差1.5、0.89、0.83、0.7、0.25，R5与R0最为接近，即NCFLM 函数曲线与L0范数的函数曲线最为相近，逼近程度最高。

图2 基于不同惩罚因子的函数值及模型近端算子函数值对比Fig.2 Comparison of function values and proximal operator function values based on different penalty factors

图2b 为不同惩罚因子的近端算子对比，惩罚因子ϕ(x,a)的近端算子θ为

当0≤a≤1/λ时，近端算子θ变为连续的非线性阈值函数：

若a=0，近端算子转化为软阈值函数，基于L1范数的近端算子是软阈值函数，其低估了较大的非零奇异值。这些惩罚因子的近端算子都是固定阈值函数，sign 为符号函数，当阈值变化时θ可转化为

由图2 可知，在信号系数较大时，NCFLM与L0范数的曲线重合，而其他惩罚因子的近端算子曲线都与L0范数所对应的θ=y处存在一个固定的距离，证明在y较大时，NCFLM 的稀疏能力与L0范数持平，由此可知，融合套索化后的NCFLM 有更加优秀的稀疏性能。以斜率作为接近L0范数程度的评判标准，NCFLM 的逼近性能比arctan 惩罚函数提高了15%。以y=-3 为例，在y值相同时，NCFLM 具有最小的θ值，由式（21）可知，此时在argmin 条件下能取得更合适的x值；以θ=-3 为例，θ相同时，只需要取绝对值更小的y值就可以满足式（21）相同的稀疏重构结果。由上述分析可知，相比于其他模型，本文的NCFLM 惩罚因子更接近理想的L0范数，逼近程度更高，能更好地反映信号的稀疏特征。

2 模型对比试验

2.1 试验平台

为验证基于NCFLM 的电机轴承复合故障诊断方法的可行性，使用昆明理工大学旋转机械故障综合模拟试验平台对外圈和内圈轴承故障电机进行试验验证。图3为试验平台，包括变频调速三相异步电机（型号为101-19-01，额定转速为3 000 r/min，最高转速为5 000 r/min）、弹性联轴器（型号为d14-e18+d18-e18）、磁粉制动器（额定扭矩12 N·m）、加速度传感器（型号为JF2100）、电机控制仪和负载控制仪。故障电机右侧的旋转轴通过弹性联轴器与磁粉制动器左侧的制动器轴相连，故障电机电源线接在电机控制仪的“电机电源”孔位，磁粉制动器线缆接在负载控制仪的“磁粉制动器”孔位，加速度传感器安装于故障电机上的传感器接口位置，采集振动信号并传输至数据采集仪中，再通过数据采集仪传输至电脑终端进行数据分析。

图3 故障电机模拟试验平台Fig.3 Faulty motor simulation experiment platform

表1 电机轴承参数Table 1 Motor bearing parameters

2.2 基于NCFLM 模型的复合故障诊断流程

基于NCFLM 的电机轴承复合故障诊断方法的流程图如图4 所示，主要包括以下步骤：

图4 基于 NCFLM 的电机轴承复合故障诊断方法流程图Fig.4 Flow chart of motor bearing compound fault diagnosis method based on NCFLM

1）通过试验平台采集三相异步电机轴承复合故障的振动信号；

2）对arctan-NCTVD 模型中的惩罚函数项进行基于GMC 非凸惩罚函数的融合套索化处理，构造新的NCFLM 模型；

3）通过一系列稀疏性能指标评判NCFLM 模型与arctan-NCTVD 模型的优劣性；

4）将采集到的复合故障信号导入新模型中，并引入FBA 算法进行求解，同时约束正则化参数和凸性参数，即可得到可准确识别复合故障的稀疏字典。

2.3 结果与分析

图5 为各模型对采集信号进行稀疏重构后的原子分布情况，为避免幅值较小的原子造成信息冗余，将幅值绝对值小于0.2 的原子定义为零原子，图5a、图5b 和图5c 中的零原子数目分别为8 600、9 269 和10 125个，NCFLM 模型处理后的结果更为稀疏，其原子压缩数目比arctan-NCTVD 增大了9.2%。NCFLM 的惩罚项在相邻原子之间进行相似估计，融合一些特征相同的原子，并将幅值绝对值较小的原子向原点压缩，在一定程度上减少了信息量较少的原子数目，降低运算复杂度。图5a和图5b 中的模型原子过于稠密，原子复杂度较大，难以满足解非凸优化的稀疏性要求。由图6 中3 种模型的收敛曲线对比可知，NCFLM 模型收敛速度快于其他模型，在函数值收敛时，arctan-NCTVD 和NCFLM 的初始函数值分别为10 000 和9 297，收敛函数值分别为1 482 和174，NCFLM 的收敛速度比arctan-NCTVD 提高了6.6%。

图5 经不同模型稀疏重构后的原子分布图Fig.5 Atomic distribution diagram after sparse reconstruction by different models

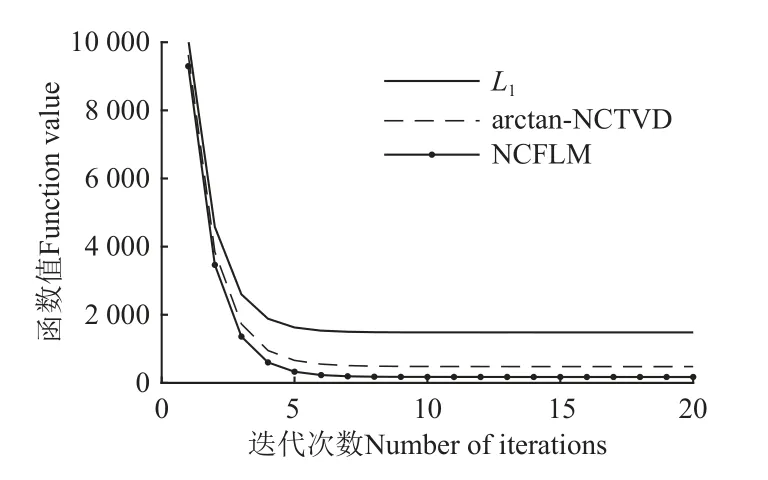
图6 不同模型的收敛曲线Fig.6 Convergence curves of different models

图7 为2 种模型的重构误差M随正则化参数λ1和λ2的变化曲线。随着λ1从0 增加到2，arctan-NCTVD的M值从0.154 增大到0.903，NCFLM的M值从0 缓慢增加到0.683 且一直比前者小；arctan-NCTVD 没有λ2项因此其M值保持在0.45，随着λ2从0 增加到2，NCFLM的M值从0.165 缓慢减小到0.043，NCFLM 的重构误差更小。图8 为2 种模型的稀疏度k和正则化参数λ1和λ2的变化关系。信号的稀疏度是指信号向量中非0 元素的个数，随着λ1从0 增加到2，arctan-NCTVD 的稀疏度从32 768 缓慢下降到7 277，而NCFLM 从32 768 下降到1 822，NCFLM 比arctan-NCTVD 需要更少的元素来进行稀疏表示。同理，λ2相同时也可得到相同的结论。在重构误差为0～1 时，分别计算图7a、图7b在λ1从0到2和λ2从0 到0.8 时各模型重构误差的变化值，结果取平均值，可得NCFLM 的重构准确度比arctan-NCTVD 提高了10%；同上，在稀疏度方面NCFLM 的性能比arctan-NCTVD 提高了46.2%，由上可知，NCFLM 的稀疏性能更优。

图7 不同模型的重构误差与正则化参数的关系对比Fig.7 Comparison of relationship between reconstruction errors and regularization parameters of different models

图8 不同模型的稀疏度与正则化参数的关系对比Fig.8 Comparison of the relationship between sparsity and regularization parameters of different modelss

综上所述，NCFLM 的原子压缩数目、收敛速度、重构准确度、稀疏度和L0范数逼近程度分别比arctan-NCTVD 提高了9.2%、6.6%、10%、46.2%和15%，因此NCFLM 模型更具优越性。

3 诊断结果与分析

前面已证明NCFLM 在稀疏性能指标方面比arctan-NCTVD 更具优势，本节展示NCFLM 的最优参数选取方法和复合故障诊断结果。

3.1 遍历寻找最优参数

图9 为电机外内圈复合故障轴承振动信号标准化处理后得到的时域及频域波形，可见频谱中识别不了fo和fI，因此无法识别轴承复合故障特征频率及其倍频成分。

图9 电机轴承复合故障信号波形图Fig.9 Waveform diagram of motor bearing compound fault signal

在进行NCFLM 处理前，需要对模型进行正则化参数选取。本文采用遍历寻参的方法来确定最优正则化参数λ1和λ2。

对图9a 的观测信号进行分析，试验中发现若λ1选取较大值，会抑制冲击成分导致结果失真，本文选取λ1范围为[0,2]，寻参过程中步长设置为0.2，文献[29]算法中参数λ2范围为[0,1)，步长设置为0.1，通过相关峭度CK刻画总体重构效果，如图10 所示，最大相关峭度CK=10.2，此时λ1=2，λ2=0.8。

图10 遍历寻找最优参数过程Fig.10 Traversal to find optimal parameter procedure

3.2 复合故障诊断结果

arctan-NCTVD 模型和NCFLM 模型的外内圈复合故障结果如图11 所示，图11a 表明arctan-NCTVD 模型虽然可初步提取外圈故障冲击成分，但是会淹没内圈故障特征；并且在恢复信号特征的过程中大量衰减信号能量，从而导致故障特征不明显。

图11 不同模型的复合故障诊断信号频域波形图Fig.11 Frequency domain waveform diagram of composite fault diagnosis signal with different models

图11b 表明NCFLM 可检测到外圈和内圈故障特征频率以及转频的调制边频带，且幅值更大，噪声更少。综上，NCFLM 在处理轴承外圈和内圈复合故障信号时比arctan-NCTVD 模型更具有优越性。

4 结论

本文基于arctan-NCTVD 模型并借鉴融合套索模型的思想，将原模型进行GMC 套索化构造了NCFLM 模型，解决了原模型无法准确识别复合故障和稀疏性能欠佳的问题，通过对自制故障电机试验平台的实测信号验证、对比和分析得到了如下有益结论：

1）NCFLM 的原子压缩数目、收敛速度、重构准确度、稀疏度、L0范数逼近程度分别比原始arctan-NCTVD 模型提高了9.2%、6.6%、10%、46.2%和15%，验证了NCFLM 的优越性；

2）所提的NCFLM 方法成功提取了由外圈和内圈局部损伤引起的周期性冲击特征，验证了本文方法的可行性和工程实用性。

NCFLM 作为一种基于信号稀疏表示的方法，其分析结果往往会受到电机轴承的时变转速和负载的影响，定工况下的复合故障诊断方法失效，故障类型会更加难以评估。因此，如何根据变工况下复合故障演变规律以及该振动信号的时频域特征构造出重构性能更强的稀疏分解模型和指标，并针对重构结果获得更准确的故障识别和分类效果，这将是之后研究工作中的重点之一。