基于VMD 的谷物清选筛振动分析与结构优化

庞靖，林毅，王升升，杜哲，谢乐乐，陈新奇,2

（1. 河南科技大学农业装备工程学院，洛阳 471003；2. 洛阳智能农业装备研究院有限公司，洛阳 471003）

0 引言

随着农业机械化进程的不断推进，农业装备的作业质量、可靠性等也需不断提高。振动是任何结构都具有的固有特性，对机械装备的振动特性被广泛关注。联合收获机作为田间收获作业的重要装备，其复杂的振动特性不仅会影响机器的可靠性和寿命，也会造成难以预料的作业损失[1-4]。

目前国内外对于联合收获机的相关研究主要包含整机振动测试[1-3]、应力分析[4]、有限元模态分析与模态试验[5]、清选筛内部气流场分析[6]、作物特性研究[7-8]以及关键结构的优化设计等[9]。张黎骅等[9]针对大豆玉米套作场景下的收获机清选作业质量问题，设计了一种应用于大豆玉米兼收的收获机清选装置，使用流固耦合和台架试验探究了振动频率、上下筛倾角等对含杂率和损失率的影响，并得到了工作指标最优的影响因子组合；刘鹏等[10]以多参数可调的清选系统为分析对象，对大豆联合收获作业中的清选参数进行了研究，得到了鱼鳞筛开度、风机转速和作业速度等因素组合对损失率等指标的影响；李永磊等[11]对所提出的批次式种子清选机橡胶球清筛装置测定了橡胶球的激振力，探究橡胶球激振力对清选性能的影响；张学军等[12]针对油葵联合收获中籽粒含杂率和损失率偏高的问题，以振动频率为因素之一，探究其对籽粒损失率和含杂率的影响；LI等[13]针对谷子联合收获时的清选效率问题，以探究自主设计的双风机振动筛谷子清选装置的工作性能为目标，设计了因素试验，其中，筛体振频是其考虑的因素之一。EBRAHIMI等[14]构建了描述联合收获机割台振动的有限元模型，使用频域分解法对割台在运行状态下的振型参数进行了估计，发现在50 Hz 附近存在共振，采用质量变化策略估计割台振动系统的频响函数矩阵，最终，通过优化割台结构，使得割台的第五阶振型50 Hz 的固有频率降低为48 Hz，有效地降低了割台的共振情形；YILMAZ等[15]针对联合收获机作业中的噪声振动问题，使用两个加速度计和两个麦克风采集传统联合收获机脱粒过程的噪声和振动，得到了发动机是主要的激振源；GALKIN等[16]针对谷物振动气动分选机清种效率低、损失率高等问题，推导了分选机在工作时种流的理论运动模型，计算了颗粒物料分层的气流速度和物料表面的流动速度，研究结果表明，使用改进型振动气动分选机在进行谷物清选时，可降低30%～50%的功耗，减少1.5 倍的种子损失。

综上，目前针对联合收获机的相关研究已取得了较多的成果，但有关清选系统振动特性研究的相关文献相对较少。清选是联合收获机作业流程中的重要一环，由于加工、装配误差，以及清选筛在机器作业时受到的复杂外界激励，会引起清选筛的不平衡振动，进而加剧清选筛关键部件的磨损，影响其清选性能，导致含杂率增高等问题。因此，本文将基于动态信号分析理论中的变分模态分解（VMD，variational mode decomposition）结合峭度及模糊熵等指标对谷物清选系统进行振动测试与分析，围绕其中因转子系统不平衡而造成的不平衡振动问题，对采集到的原始信号进行VMD 分解和特征提取，然后使用惩罚函数法完成对清选筛转子系统的结构优化。以期提高联合收获机械作业稳定性并为其减振分析提供参考。

1 谷物清选系统组成及工作原理

谷物清选系统结构简图如图1a 所示，主要包括风机1、筛箱2、筛体3 和筛体驱动装置4。清选系统模型如图1b，其中，驱动装置为曲柄滑块机构，筛体上筛为鱼鳞筛、下筛为编织筛。在风机作用下，筛箱内部形成风场，由于谷物脱出物空气动力学特性的差异，将其中的轻质杂余吹出筛箱；动力通过链传动传输至曲柄，曲柄带动筛体运动，除了驱动装置，上筛和下筛分别通过螺栓固定在筛体支架上，随着筛体运动而振动，籽粒落在筛体网面上受到振动落入网面空隙而达到清选的目的。

图1 清选系统结构示意图Fig.1 Schematic diagram of cleaning system structure

在清选系统工作时，受自身结构以及一些外部激励的作用，造成转子系统不平衡，使得整个装置振动不平衡，进而影响清选筛的工作效率与寿命。因此，需要对清选筛的振动特性进行研究。

2 驱动机构转子系统不平衡分析

2.1 驱动机构转子系统组成

本研究的驱动机构转子系统示意如图2 所示，主要由轴承座、偏心轮、中间轴、筛体连接盘、驱动链轮和配重盘等组成。其中，配重盘的质量为3 500 g，质心与驱动链轮中心的距离为135 mm，中间轴轴径为41 mm，偏心轮和筛体连接盘以及中间轴之间通过一对轴承连接；中间轴通过轴承固定在轴承座上，实现动力的传递。

图2 驱动机构转子系统模型Fig.2 Driving mechanism rotor system model

2.2 转子系统动力学模型

根据有限元分析理论，转子系统可描述为由轮盘单元、轴段单元和轴承座单元组成的系统整体，其中，各个单元之间通过节点来联结。根据转子动力学理论，转子系统的运动方程可分解为各个单元的运动方程。拉格朗日方程是建立转子系统动力学模型主要的广义模型[17]，其数学表达式为

式中T为系统总动能（J）；V为系统总势能（J）；qi为广义坐标；Qi为系统所受广义力（N）。

假设刚性轮盘单元质量为m1、外径为D1、内径为D0、极转动惯量为J1，轮盘单元的惯性力主向量在空间坐标系中x轴和y轴上投影的坐标为(x1,θy)和(y1,-θx)，则该轮盘单元处节点位移可表示为：u1=[x1,θy]T，u2=[y1,-θx]T。

基于拉格朗日方程可进一步求得轮盘单元的动力学方程为

式中Qwdk(k=1,2)为轮盘单元所受的广义力(N)。

同理可得轴段单元的动力学方程为

式中Ms为轴段单元的运动惯性矩阵，ΩJs为回转矩阵，Ks为刚度矩阵，Qks为轴段单元所受的广义力(N)。

对于轴承座单元的动力学分析，不仅要考虑其固体接触，也要分析油液接触，基于Hertz 接触理论，受到载荷的作用时，假设两构件接触时一构件的粗糙表面微型凸起与另一构件刚性结合面接触时的真实接触半径为r1，不考虑变形时两构件接触半径为r2。根据Lankarani-Nikravesh 碰撞接触模型[18]，综合考虑两碰撞体的材料属性、碰撞体间的相对碰撞速度及碰撞体的局部变形等信息可得固体接触部分碰撞力模型为 δ(-)为两部件碰撞相对速度（m/s）。

式中K'为接触刚度系数，δ为碰撞刺穿深度（mm），n为非线性指数（金属材料取值1.5），ce为碰撞恢复系数，

此外，轴与轴承配合之间存在润滑剂，因此，需要分析轴与轴承结合部位的液体接触。

由于间隙往往非常小，即油膜厚度很小，因此，假设油膜上的承载力方向在油膜厚度方向（y）上保持不变，且不考虑动力粘性系数μ随空间位置的变化。则基于液体平均流动的广义雷诺方程，轴与轴承之间油膜流动的动力学方程可表示为[19]

式中∇2为拉普拉斯算子，div 为散度，Fi(i=x,y,z)为作用在油膜内部微元体内所有质量上的力。

2.3 驱动机构转子系统不平衡分析

旋转件的异常振动会影响整机的正常运转，转子不平衡是旋转机械的主要激振源[17]，不仅会影响转子系统的稳定性，也会加剧磨损等进而造成转轴疲劳、联结失效等。旋转件在运行中即使是很小的质量偏心也会产生较大的离心力而引发振动，对于平衡转子的常见方法包括静平衡和动平衡等。无试重动平衡法[20-21]旨在通过理论分析来代替实际测试进而对不平衡量进行估计或计算，常见的如动力学模型求解、影响系数估计和智能算法求解等。为了分析本文驱动机构转子系统的不平衡特性，将配重块视为偏心配重圆盘（如图3 所示），对偏心配重圆盘建立如下的动力学方程：

图3 偏心配重盘示意图Fig.3 Schematic diagram of eccentric counterweight plate

式中J2为偏心配重盘的极转动惯量，e为配重盘安装偏心距，m2为配重盘质量，ϕ 为转子不平衡量相位，Ω=ϕ。

最终，将各个单元的动力学方程进行综合可得转子系统响应的运动方程为

其中，M为系统各单元集成后的质量矩阵；C为各单元集成后的阻尼矩阵；K为各单元集成后的刚度矩阵；R为系统的位移向量；Q为各单元集成后的广义力向量。

针对清选筛的不平衡振动问题，假设其不平衡响应解为

c为阻尼系数；k为刚度系数。

由式（9）可求解处系数A1、A2、B1、B2，进而得到不平衡信号幅值特征矩阵。

3 不平衡振动分析

3.1 变分模态分解

变分模态分解于2014 年由DRAGOMIRETSKIY等[22]提出。该方法是一种非递归的变分分解方法，和其他信号分解方法相比，可以指定分解的模态数，在对模态函数求解过程中，采用镜像延拓有效避免了类经验模态分解在信号分解中的端点效应[23]，但对模态函数的求解前需要指定模态数、二次罚项等参数。作为一种信号分解方法，其将任何信号都假设为由一系列具有特定中心频率、有限带宽的子信号组成，基于经典维纳滤波、希尔伯特变换和混频和外差解调等原理，构建描述约束变分问题的数学表达式[22-23]，并对其进行迭代求解，得到中心频率和带宽。

3.2 模糊熵与峭度

模糊熵[24-25](FE,fuzzy entropy)是ZADEH 在1968 年提出的来描述一个模糊集模糊程度的概率学概念，该方法用均值代替绝对幅值差，以指数函数作为模糊函数来衡量两个向量之间的相似度。在信号分析中以待测信号作为样本集，计算其模糊熵YFE，YFE越大，两信号相关性越差；YFE越小，两信号相关性越好。

峭度(Kurtosis)是一种无量纲指标，该值越大，信号中所包含的冲击成分和特征信息就越丰富[26]，在正常工作状态下，轴承座处振动信号接近正态分布，峭度指标接近3[27]。而在一些不平衡冲击下，会使轴承座处振动信号偏离正态分布，不平衡振动冲击成分会混叠在原始信号中，峭度值越大，不平衡振动冲击成分特征更易于提取。因此，通过对峭度的计算可以有效的识别特征信号。其定义如下：

式中μi为本征模式分量ui的均值，σi为ui的方差。

3.3 基于VMD 及综合指标信号分析流程

尽管基于VMD 的振动信号分析在信号时间序列的预测与成分分解方面是可行的，但仅仅依靠该方法无法准确得到关于所要提取特征本身的信息。在一些研究中，模糊熵和峭度被构建为一种综合指标应用于轴承的故障诊断中[28-29]，综合指标K的定义如下：

通过综合指标K可有效的找到振动信号中包含冲击成分和特征信息最丰富的分量，进一步的，对提取后分量信号的进行包络谱分析，得到不平衡振动频率。该方法的主要步骤如下：

1）采集清选筛在不同工况下的振动数据样本，对其进行时、频域分析，选取频率成分丰富的测点采集到的振动信号进行VMD 分解，得到有限个本征模式分量ui。

2）计算各分量的综合指标，选择综合指标最小的分量作为敏感分量，用于后续的特征提取。

3）对选择的敏感本征模式分量进行希尔伯特变换求其包络谱，提取不平衡振动。

4 清选筛振动台架试验

4.1 清选筛试验台工作参数

本文所用清选筛试验台为河南科技大学自主设计的谷子切-轴流脱粒清选系统，如图4a 所示。其结构主要包含两级脱粒系统、清选系统和电机等，两级脱粒系统主要由一级切流滚筒和一级轴流滚筒以及凹板筛组成。如图4b 所示，在装置运行时，动力由电机输出，通过动力中间传动轴传输至风机上，并通过一级带传动和一级链传动传输至清选筛驱动转轴上，其次，通过带传动将动力输出到脱粒滚筒上，两级脱粒滚筒之间通过链传动。

图4 谷物清选筛试验台及其传动示意图Fig.4 Grain cleaning sieve test-bed and its transmission schematic diagram

激励源是引起结构振动的核心因素，除此之外，轴承缺陷、结构件的制造或装配误差以及旋转件的配重设计等也是重要因素。其中，外部激励源包括驱动装置或作业环境中可能存在的激励源，如地面起伏等。本文旨在分析转子系统不平衡引起的振动问题，忽略轴承缺陷、系统的制造和装配误差，且不考虑地面的激励作用，对清选筛试验台进行了传动计算和工作参数分析，其中，电机、脱粒滚筒、中间传动轴和风机为主要激励源，分别计算了其理论工作转速和激励频率，如表1 所示。

表1 试验台工作参数Table 1 Working parameters of the test bed

4.2 振动试验测试系统及方法

如图5 所示，振动试验测试系统由加速度传感器、DH5902 动态信号采集仪、计算机、变频器、异步电机和试验台架组成。其中，三向加速度传感器量程为±50 g，频响范围为0.3～6 kHz，x向、y向和z向灵敏度分别为101.1、97.3 和99.3 mV/g；单向加速度传感器灵敏度为96.1 mV/g；数据采集仪共有16个通道，最高采样频率为100 kHz。

图5 测试系统Fig.5 Testing system

为了准确反映清选筛的振动特性，对试验台进行了预试验，基于试验台的动力传动特点与主要的激励源，选择筛体支撑（筛体驱动装置支撑）轴承座为测点5、筛体尾部侧板为测点6，其次，为了反映各个激励源的实际振动特点，选择动力中间传动轴轴承座为测点1、第一级脱粒滚筒转轴轴承座为测点2、风机转轴轴承座为测点3、第二级脱粒滚筒转轴轴承座为测点4，共6个测点（图6）；其中，测点1 和3 分别布置一个单向加速度传感器，其余测点布置为三向加速度传感器，共使用DH5902 采集系统的14个通道；传感器的安装选择胶粘和磁吸两种方式，在轴承基座上（测点1、测点3）由于基座表面不平整，选择粘接对传感器进行固定，其余测点均选择磁吸方式固定。

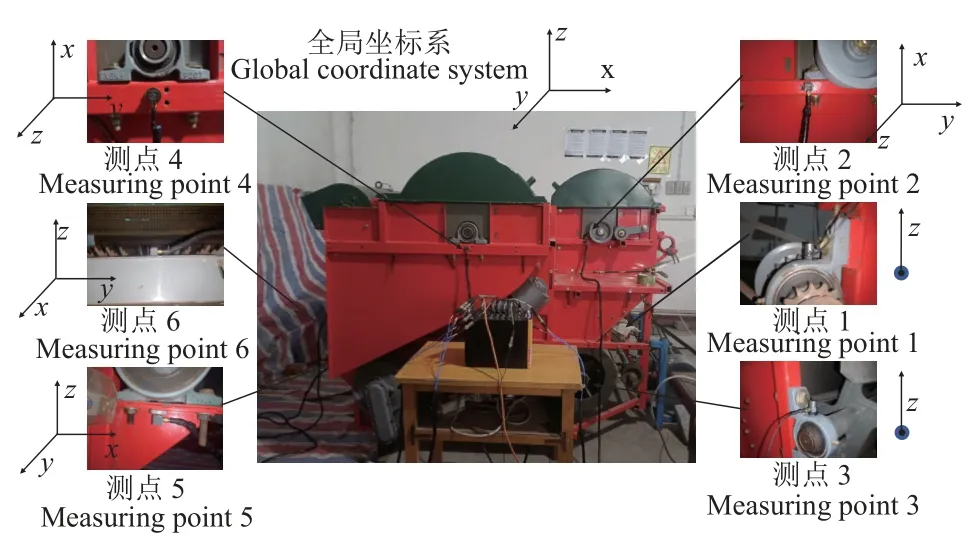
图6 试验测点布置Fig.6 Layout of test measuring points

此外，为了便于提取和分析各个加速度传感器检测的振动信号，从而更加准确的得到每个测点的振动情况，构建如图6 所示的试验台全局坐标系和各个测点的局部坐标系。以物料喂入方向为全局坐标系x方向，垂直大地方向为全局坐标系z向。测点1、3 分别检测中间传动轴和风机轴承座的径向振动，规定其局部坐标系如图6，测点2 与测点4-6 分别检测一、二级脱粒滚筒轴承座、筛体支撑轴承座和筛体尾部侧板在全局坐标系3个方向上的振动。

4.3 信号采集与时、频域分析

在完成测试系统的调试和预试验后，考虑到试验台的实际应用场景，即履带式联合收获机的作业场景，基于试验台的工作参数，以设计的动力输入轴额定转速900 r/min 为基础，并根据采样频率和采样定理，选择5 Hz为激励源的频率分辨率，分别在电机转速为300、600、900 r/min 三种工况下对6个测点进行测试。限于篇幅，选取清选筛上的测点5 和测点6 在局部坐标系3个方向上的时域信号及其均方根值如图7、图8 所示。

图7 测点5 在3个方向上的时域信号Fig.7 Time domain signals of measuring point 5 in three directions

图8 测点6 在3个方向上的时域信号Fig.8 Time domain signals of measuring point 6 in three directions

通过计算振动信号的加速度均方根值（root mean square，RMS）可见，随着转速的提高，各个测点在不同方向上的信号的RMS 值越来越大，其中，测点5、6在3个方向上信号的最大RMS 值分别为0.004、5.982、3.617、6.581、24.327 和25.123 m/s2，即振动强度越来越大；其次，三种工况下各个通道采集的信号趋势相当，随着整个装置输入转速的增大，脱粒滚筒1 和2（测点2、测点4）、清选装置尾部侧板（测点6）与筛体支撑轴承座（测点5）以及风机转轴（测点3）的振幅均呈增大趋势且信号中带有大量的噪声和不平衡成分，但中间传动轴（测点1）和筛体支撑轴承座局部坐标系x方向（测点5-x向）的振幅在0 附近波动且未有较大改变，究其原因，主要是因为中间传动轴处与轴承座的装配精度高，从而使得该部位轴在运转过程中的径向振动小。而筛体支撑轴承座处局部坐标系x方向的振幅趋近于0 说明清选筛在全局坐标系x方向的振动小，强度趋近于0，这也为下文进一步的分析提供了参考。

为了初步确定测点5、6 处的振动情况，对工况3 下测点5 在其局部坐标系y和z方向与测点6 在其局部坐标系各个方向上的振动信号进行功率谱密度计算如图9所示。

图9 转速为900 r/min 时测点5、6 不同方向功率谱密度Fig.9 Power spectral density in different directions of measurement points 5 and 6 at a rotational speed 900 r/min

其中，由于测点5-x向处信号的振动强度很小，所以不考虑在该处局部坐标系x方向上的振动。除此之外，测点5 处采集到的信号中所包含的特征频率主要分布在12、13、18、19、20、24、25、30 和36 Hz 附近；测点6 处采集到的信号中所包含的特征频率主要分布在6、12、13、18、19、20、24、25、26、30、31 和36 Hz 附近。

其中，在12、13、18、20、24、25、30 和36 Hz 附近，两个测点处均存在对应的振动。

4.4 基于VMD 及综合指标的不平衡振动提取

对于实测振动信号，其中往往夹杂着噪声和特征信号等复杂的成分，仅仅通过对实测振动信号的时、频域分析，不足以明确其准确的振动特点，需要进一步分析。

由于本文主要探讨转子质量偏心所造成的的不平衡振动问题，而测点6 主要测的是筛体尾部侧板的振动，考虑其中可能存在因零件的加工、装配误差而造成的振动，在转速为900 r/min 下，选择筛体驱动装置支撑轴承座处测点5 局部坐标系y和z方向的振动信号使用变分模态分解（VMD）法对其进行分解（如图10 所示）。有关模态个数k的选择，基于对整个装置运动特点和理论激励源的分析，初步选择k为5，7，9 进行预分解，考虑到模态混迭，最终确定k取7。之后分别对测点5局部坐标系y、z方向的振动信号进行VMD 分解。得到测点5 在局部坐标系y和z方向上信号的VMD 分量后，分别计算各分量的模糊熵和峭度，并得到综合指标K，如表2 所示。

表2 VMD 分量的特征量计算结果Table 2 Calculation results of characteristic quantities of VMD components

图10 测点5在y和z 向的VMD 结果Fig.10 VMD results of measuring point 5 in y and z directions

由表2 可以看出，在测点5 局部坐标系y和z两个方向振动信号VMD 后的7 阶本征模式分量(u1-u7)中，u1的综合指标K最小，可初步确定u1与原始信号之间的敏感性最优。

5 清选筛结构优化

5.1 驱动机构转子系统不平衡模型计算

为了减小因驱动机构因转子系统不平衡而造成的清选筛不平衡振动，应尽可能的使不平衡量最小，即不平衡振动信号幅值尽可能小。基于清选筛曲柄滑块机构的设计参数，选择配重盘质量m2和安装偏心距e的优化区间分别为[500g,5 000g]和[41mm,200mm],利用约束优化方法建立了驱动机构转子系统的不平衡优化数学模型如下：

其中：ψ=[m2,e]为优化变量矩阵。

然后通过惩罚函数法[29]利用SUMT 程序在Matlab中完成优化参数的计算。

其运算过程为：首先随机选取优化变量初始值ψ0、惩罚因子初值r0（根据经验公式试算选择）和缩减系数c（经验取值在0.1～0.7 之间），然后根据收敛条件依次迭代k次，满足收敛条件后迭代结束，输出约束最优解ψ*。将驱动机构转子系统的不平衡优化数学模型导入SUMT 程序中，通过Matlab 进行计算后得到：m2=3 650 g，e=136.7 mm。

5.2 优化效果验证

在转速为900 r/min，优化前后测点5 局部坐标系y和z方向上采集的振动信号进行VMD 分解并对其敏感分量进行包络谱分析如图11 所示。

图11 优化前后测点5在y和z 两个方向敏感分量包络谱分析结果Fig.11 The envelope spectrum analysis results of the sensitive component of the measuring point 5 in y and z directions beforeand after optimization

从图11 可以看出，在30.13 Hz 处振动强度最大，分别为0.29 和0.24 dB。此外，基于4.1 节有关激励源的分析，剔除激励源附近的频率点，选择30.13 Hz 为不平衡振动的主要特征频率。

相比优化前，优化后在30.13 Hz 的不平衡冲击振动强度分别为0.12 dB 和0.11 dB，相较于优化前的0.29和0.24 dB，振动能量最大下降了58.62%，证明了对驱动机构转子系统优化的有效性。

6 结论

本文针对谷物清选筛的振动问题，基于VMD 及综合指标对清选筛实测振动信号进行分解、特征提取和驱动机构的优化。基于动态信号峭度和模糊熵所构建的综合指标对VMD 后的模式分量进行计算、选取敏感分量，最后分析敏感分量的包络谱确定不平衡振动的特征频率，主要结论如下：

1）基于VMD 信号分解的特征提取方法及由峭度和模糊熵构建的综合指标，通过选择最优模式分量并计算其包络谱，能够有效的提取信号中的特征成分，在谷物清选筛不平衡振动分析与减振分析中具有良好的实用性。此外，也可为其他结构的振动分析提供参考。

2）通过计算清选筛筛体支撑轴承座处信号VMD 后本征模式分量的综合指标，得到第1 阶本征模式分量的综合指标最小，分别为0.706 和0.241，选择第1 阶本征模式分量为原始信号敏感分量并计算其包络谱，得到在电机转速(即动力输入轴转速)为900 r/min 时，清选筛的不平衡振动主要在30.13 Hz 处。

3）采用惩罚函数法建立了清选筛驱动机构转子系统的结构优化函数并进行计算。优化前30.13 Hz 处的振动强度在0.24～0.29 dB；优化后转子系统配重块质量为3 650 g，距轮盘中心的偏心距为136.7 mm，30.13 Hz处的振动强度在0.11～0.12 dB。