物料-干燥箱一体化的香菇热风干燥模拟方法及应用

胡如响，孙东亮,*，朱跃强，卢星宇，王 鹏，宇 波

（1.北京石油化工学院机械工程学院，北京 102617；2.西安交通大学能源与动力工程学院，陕西 西安 710049）

果蔬类农产品是人类生产生活所必需的食物，其新鲜采摘后的含水率大部分高达85%以上，高含水率给长期贮存和长距离运输带来了巨大困难，农产品干燥技术应运而生。干燥作为一种延长水果、蔬菜等高含水率食品贮存时间的方法，主要通过降低含水率以降低水的活性和抑制微生物的生长繁殖，从而达到延长贮存时间的目的[1]。目前最常用的干燥技术为热风干燥，但干燥过程中存在产品品质降低、耗时等缺陷，且干燥过程是一个复杂的传热传质过程，影响因素众多，一直备受学者们的关注[2-6]。

在现有的农产品热风干燥研究中，主要分为试验研究和模拟研究。试验研究中大部分聚焦于通过大量试验探究提升产品品质和降低干燥能耗的方法[7-11]，存在周期长、耗材量大等缺陷。而在热风干燥的模拟研究中，大部分的研究聚焦于物料层面，通过描述单个或几个物料的热风干燥过程，探究物料内部的传热传质过程以及物料的变形、干燥条件对产品品质的影响等[12-15]。而在实际工程应用中干燥条件多变且分布不均匀，所以物料层面的研究无法考虑到干燥箱内流速、温度和湿度不均匀性的影响，导致结果与实际情况不相符。基于此，部分学者对干燥箱层面的热风干燥模拟展开了研究。Smolka[16]和Kjær[17]等通过模型模拟研究了干燥箱内干燥参数的分布情况，并采用不同方法降低了干燥参数的分布不均匀性，但是他们采用的模型中没有考虑物料对流场、温度场和湿度场的影响，与实际情况偏差较大。这是因为在干燥过程中物料内的液态水吸热蒸发成水蒸气，会加剧温度场和湿度场的分布不均匀性。为了解决这一问题，Wang Peng等[18]尝试将物料和干燥箱进行耦合，并将人参堆积区域假定为多孔介质，考虑了人参对流场、温度场和湿度场的影响。但在这项研究中人参干燥过程中的水分蒸发速率被设置为常数，没有考虑干燥速率在时间和空间上的变化，与实际的干燥过程不符。

综上，目前干燥箱规模的热风干燥模拟研究重点主要集中在干燥箱方面，缺乏对物料本身干燥过程的分析，没有真正将物料与干燥箱耦合起来。为解决这一问题，本研究构建了物料-干燥箱一体化的香菇热风干燥模拟方法，并通过模拟结果分析了香菇干燥过程中的干燥不均匀性。

1 材料与设备

1.1 材料

新鲜香菇（Lentinus edodes）购自北京某生鲜超市，初始湿基含水率约为88.56%，选取质量和体积相似的香菇装入密封袋后贮存在医用冷藏箱中（（4±1）℃）。

1.2 仪器与设备

多功能干燥机（图1） 常州一步干燥设备有限公司：干燥箱（1.42 m×1.20 m×1.65 m）、YX3-905-2循环风机（额定功率为1.5 kW） 江苏运中电机股份有限公司；LDR0.016-0.7蒸汽加热器（额定功率为12 kW）张家港威孚热能股份有限公司；XKY-1H热泵（额定功率为1.05 kW） 中山爱美泰电器有限公司；YC-100医用冷藏箱 澳柯玛股份有限公司；BSA220.4电子分析天平上海卓精电子科技有限公司；XY-100MW卤素水分分析仪常州市幸运电子设备有限公司。

2 物料-干燥箱一体化的香菇热风干燥模拟方法

2.1 定工况条件下香菇干燥动力学模型

2.1.1 定工况条件下香菇热风干燥试验

待试验前取出香菇晾至室温并去掉菇柄，保留约1 cm蒂根，单层平铺于干燥架隔板上，每一层平板平铺9 列13 行，总共12 层（图2）。在实际的工业生产过程中，香菇热风干燥的温度多为50～60 ℃，风速多为2～4 m/s，故本试验的空气温度设置5 个水平，分别为45、50、55、60 ℃和65 ℃，风速设置5 个水平，分别为1、2、3、4 m/s和5 m/s，相对湿度设置了5 个水平，分别为0.25、0.30、0.35、0.40和0.45，进行3因素5水平的正交试验，如表1所示。试验过程中，选取第1层上第1列的香菇，利用电子分析天平每0.5 h测定其质量变化，重复测定3 次取平均值。干燥至GB 7096—2014《食品安全国家标准 食用菌及其制品》规定的香菇安全贮存标准以下，即湿基含水率不高于13%[19]，随后将样品密封、常温保存。

表1 热风干燥试验工况Table 1 Experimental conditions of hot air drying

图2 香菇在干燥箱中的排列方式Fig.2 Arrangement of Lentinus edodes in the drying chamber

2.1.2 试验参数的获取

干基含水率Mt的计算如公式（1）所示。

式中：mt为干燥至t时刻香菇的质量/kg；md为香菇的干基质量/kg；Mt为干燥到t时刻香菇的干基含水率/（kg/kg）。

水分比（moisture rate，MR）的计算如公式（2）所示。

式中：Me为干燥结束时香菇的干基含水率/（kg/kg）；M0为初始时刻香菇的干基含水率/（kg/kg）。

农产品干燥过程中水分比随时间的变化通常用干燥动力学模型描述，目前常见的干燥动力学模型主要有Newton、Page等半理论模型，如表2所示。

表2 常见的干燥动力学模型Table 2 Common drying kinetic models

根据表2中常见的干燥动力学模型，可以将其写成统一的形式，如式（3）所示。

式中：t为干燥时间/h；A、B、C均为拟合参数。本研究将采用式（3）拟合试验数据。

为了评价数据拟合后的效果，通常使用决定系数R2、离差平方和χ2、均方根误差（root mean square error，RMSE）和平均相对误差e来说明拟合结果的准确性，R2的值越接近1，χ2、RMSE和e的值越接近于0，说明拟合结果的准确度越高，效果越好[26]。上述4 个评价指标分别采用式（4）～（7）进行计算[27]。

式中：MRexp为水分比的试验值；MRpre为水分比的拟合预测值；n为试验数据的总数；m为模型中参数的个数。

2.1.3 定工况条件下干燥动力学模型

通过上述试验已经得到了不同工况下香菇的质量随干燥时间的变化情况，利用Origin软件对试验结果进行处理，采用式（3）进行干燥动力学模型拟合，可以得到不同试验工况下香菇的干燥动力学模型和对应模型的统计分析结果，如表3所示。

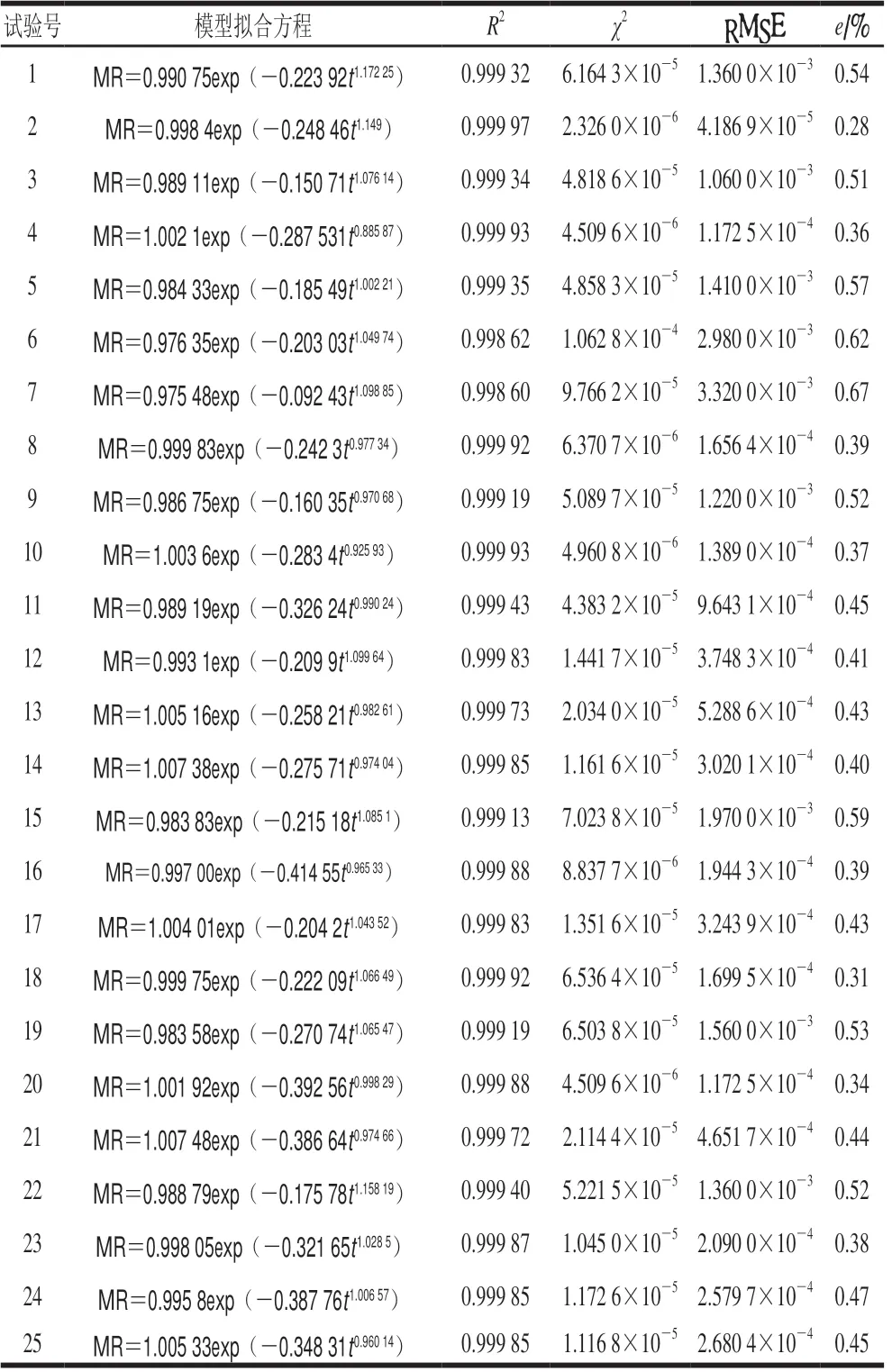
表3 不同工况下的模型拟合方程及统计分析结果Table 3 Fitting model equations under different conditions and their figures of merit

通过表3中的统计分析结果可以看出，R2的值均大于0.99，且χ2和RMSE的值均接近于0，以干燥试验数据为对照，对回归模型进行验证，试验数据和拟合值的平均相对误差e小于1%，说明常见干燥动力学模型的通式（3）对于香菇在定工况条件下的热风干燥试验数据具有较高的预测精度。

分别建立式（3）中拟合参数A、B、C关于空气温度、空气相对湿度和风速的回归关系，如式（8）～（10）所示。

式中：T为空气温度/℃；RH为空气的相对湿度；U为风速/（m/s）。

以空气温度50 ℃、相对湿度0.35和风速3 m/s的干燥试验数据为对照，对模型通式及各拟合参数的回归关系进行验证，验证结果的R2为0.993 7，表明模型的预测效果较好。说明模型通式（3）及其参数的多元回归模型描述香菇在定工况条件下热风干燥的干燥动力学是可行的。

2.2 变工况条件下香菇干燥动力学导数模型

上述香菇的干燥动力学模型虽然能够预测在定工况条件下香菇干燥过程的水分比变化，但是在实际工程应用中，由于物料较多，吸热蒸发产生的水蒸气会影响干燥箱内的温度场和湿度场，致使干燥箱中的工况处于动态变化中，所以上述定工况下的香菇干燥动力学模型不再适用，而且难以应用于干燥过程的计算流体力学（computational fluid dynamics，CFD）数值模拟之中。为了更好地解决上述问题，本试验推导了适用于变工况下的香菇干燥动力学导数模型，并基于该导数模型得到了香菇内部液态水的蒸发速率。

以下基于定工况条件下的干燥动力学模型（3），给出变工况条件下香菇干燥动力学导数模型的推导过程。首先将通式（3）对时间求导，得到求导后的方程，如式（11）所示。

再将通式（3）代入到式（11）中，得到式（12）。

最后将拟合参数与干燥工况参数之间的多元回归关系式（8）～（10）代入式（12）中，即得到能够适用于变工况参数条件下的香菇热风干燥动力学导数模型。由式（12）可知，该导数模型中不含有时间项，只含有水分比和工况参数，所以能够保证在实际求解应用过程中水分比的连续性，可以用来预测变工况条件下香菇热风干燥过程中的水分比变化。

在上述变工况条件下香菇热风干燥动力学导数模型的基础上，本研究提出了一种能够适用于变工况条件下香菇内部液态水蒸发速率的计算方法。首先，单位体积内香菇液态水的蒸发速率可以用式（13）进行表示[28]。

然后将变工况条件下的导数模型（12）带入到式（13），最终可以得到香菇内部液态水的蒸发速率，如式（14）所示。

由于拟合参数A、B、C是空气温度、空气相对湿度和风速的多元回归关系，因此能够将香菇内的水分蒸发速率与干燥箱内部的工况变化过程联系在一起，充分考虑时间和空间上的变化，进而能够用于准确计算在变工况条件下香菇热风干燥过程中的水分蒸发速率。

2.3 物料-干燥箱一体化的模型构建

2.3.1 物理模型及网格划分

针对该试验所用的干燥箱尺寸和香菇的排列方式（图2），对物料和干燥箱建立一体化的物理模型，如图3所示。主要将干燥箱内部划分为两个区域，分别为空气自由流动区域和香菇平铺区域。

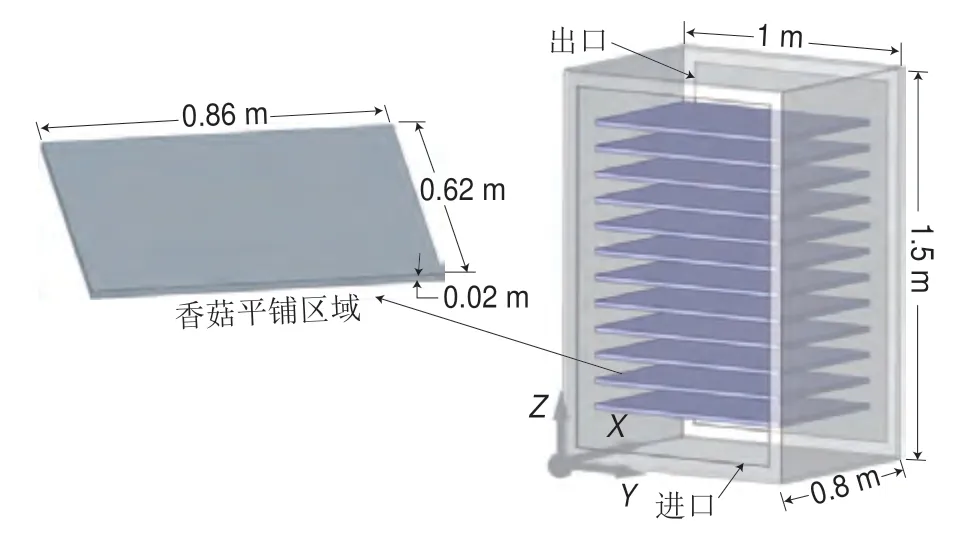
图3 物料-干燥箱一体化的物理模型Fig.3 Physical model of material-drying oven integration

由于计算区域相对规整，所以选用结构化网格划分计算区域。另外考虑到香菇平铺区域同时存在流动、传热传质和香菇失水形变等复杂的物理现象，所以对此区域进行了加密处理，网格划分结果如图4所示。

图4 物料-干燥箱网格划分Fig.4 Mesh generation of material-drying oven integration

2.3.2 数学模型

在热风干燥过程中，热空气从香菇表面流过，通过对流换热作用使香菇的温度上升，内部的水分不断蒸发，产生的水蒸气在压差和扩散的作用下转移到香菇的表面并被热空气不断带走。所以干燥过程是一个流动、传热和传质的耦合过程。

控制方程基于如下假设建立：在香菇平铺区域，香菇之间存在充满空气的孔隙，所以将此区域假设为多孔介质，由热空气和香菇组成，其中香菇被假设为固体；热空气为不可压缩理想气体；香菇平铺区域保持局部非热平衡，即热空气与香菇的温度不同；由于空气流速较高，以强迫对流为主，故不考虑重力的影响。

2.3.2.1 流动方程

在干燥过程中，干燥箱入口风速在1 m/s及以上，雷诺数大于等于5.6×104，所以干燥箱内部为湍流流动[29]。连续性方程和动量方程分别如式（15）和式（16）所示。

式中：u为矢量风速/（m/s）；ρg为热空气的密度/（kg/m3）；p为干燥箱内的相对压强/Pa；νg为热空气的运动黏度/（m2/s）；νT为热空气的湍流黏度/（m2/s）；F为动量源项。

在自由流动区域，热空气没有额外的阻力，所以该区域的动量源项F为零。在香菇平铺区域，由于被设定为多孔介质，所以热空气在该区域的流动受多孔介质阻力的影响，根据Darcy-Forchheimer定律[30]，多孔介质内的流动阻力分为与流速成正比的黏性阻力和与流速的平方成正比的惯性阻力两部分，采用Ergun公式（式（17））计算动量源项F。

式中：φ为孔隙率；dep为当量直径/m。

2.3.2.2 能量方程

在自由流动区域，只有热空气存在，根据能量守恒定律，该区域的能量方程如式（18）所示。

式中：Cp,g为热空气的比热容/（J/（kg·℃））；λg为热空气的导热系数/（W/（m·℃））。

在香菇平铺区域，存在气相的空气和固相的香菇，由于两者的温度相差较大，所以采用局部非热平衡模型描述该区域的传热过程。根据局部非热平衡假设[31]，多孔介质内各相温度不相等，所以要为热空气和香菇分别建立能量方程，建立的能量方程分别如式（19）和式（20）所示。

式中：hAlg（T1－Tg）表示多孔介质内热空气与物料的对流换热量/J；h为空气与物料之间的对流换热系数；Alg为界面面积密度/m－1；T1为香菇的温度/℃；Tg为热空气的温度/℃；ρ1为香菇的初始密度/（kg/m3）；Cp,1为香菇的比热容/（J/（kg·℃））；λ1为香菇的导热系数/（W/（m·℃））；表示香菇内部液态水蒸发消耗的蒸发潜热/（J/kg）。

2.3.2.3 传质方程

热风干燥过程中，自由流动区域和香菇平铺区域都存在水蒸气的传质过程，这主要是由于压差形成的对流和浓度扩散造成的[32]。因为香菇内部的水分蒸发后会被周围的热空气带走，所以只有香菇平铺区域的传质方程存在质量源项。自由流动区域和香菇平铺区域的传质方程分别如式（21）和式（22）所示。

式中：ω为空气中水蒸汽的质量分数/%；Dva为扩散系数/（m2/s）；为质量源项，即香菇内部液态水的蒸发速率/（kg/（m3·s））。

本研究中，每次干燥箱中香菇的数量都达到上千个，而在实际的工程应用中，干燥的香菇数量会更多，因此在这种情况下对每个香菇进行建模计算其内部的水分蒸发速率是不现实的，所以这里采用前文推导得到的式（14）对香菇内部液态水的蒸发速率进行计算。由式（14）可知，香菇内部液态水的蒸发速率的计算与拟合参数相关，而拟合参数又是空气温度、空气相对湿度和风速的回归关系，因此实现了香菇内部液态水的蒸发速率与传热传质方程的耦合，充分考虑了香菇吸热蒸发过程和干燥箱内工况环境变化的相互影响，实现了物料与干燥箱的真正耦合，最终构建了符合实际干燥过程的物料-干燥箱一体化香菇热风干燥模型。

2.3.3 边界条件

入口边界和出口边界的位置如图3所示，其中入口边界的空气温度、相对湿度和风速为固定值，湍动能和湍流耗散率分别由式（23）和（24）确定，出口边界为自由流动出口。干燥箱其余壁面具有良好的保温特性，为绝热壁面，速度和水蒸气质量分数分别为无滑移和零法向梯度条件；壁面湍流采用壁面函数，湍动能的法向梯度为零，湍流耗散率由式（25）确定。

式中：ωwall为壁面的湍流耗散率；ωVis为黏性底层（壁面的法向距离的无量纲量y＋＜5）的湍流耗散率；ωlog为对数律层（y＋＞30）的湍流耗散率。

2.3.4 模型参数

2.3.4.1 孔隙率

香菇在干燥过程中会发生收缩，且收缩率与水分比之间呈如式（26）的函数关系[33]，这使得香菇的体积会随着干燥过程不断减小，对应的孔隙率会不断增大，所以孔隙率由式（27）计算。

式中：SR为香菇的收缩率；V1为香菇的体积/m3；Vg为香菇平铺区域空气的体积/m3；V1,0为香菇初始时刻的体积/m3。

2.3.4.2 等效直径

对于非球形粒子填充的多孔介质，用式（28）、（29）求解等效直径可使多孔介质阻力的计算误差最低[33]。

式中：φ为球形度；A1为单个香菇物料的表面积/m2；As1为与单个香菇体积相同的球的表面积/m2。

在干燥过程中，香菇会发生收缩，对应的等效直径也会发生变化。香菇的菌盖直径约为0.07 m，高度约为0.02 m，形状和球冠类似，所以本试验采用球冠的相关公式计算香菇的体积和表面积。假设香菇各向同性，在各个方向上均匀收缩，则等效直径可进一步表示为式（30）。

式中：dep,0为初始时刻香菇的等效直径/m。

2.3.4.3 界面面积密度

界面面积密度是固体与流体交界面的面积和多孔介质总体积的比值，即本研究中香菇的表面积和香菇平铺区域体积的比值。香菇在干燥过程中的收缩会导致表面积减小，对应的界面面积密度也会减小，变化后的界面面积密度由式（31）计算。

式中：Alg,0为初始时刻的界面面积密度/m－1。

2.3.4.4 香菇的热物性参数

香菇主要由固体基质、水和气体组成，随着干燥过程的进行，各组分的体积分数和质量分数也会随之变化，对应香菇的密度、导热系数和比热容分别由式（32）、（33）和（34）计算。

式中：ρs为香菇固体基质的密度/（kg/m3）；ρw为香菇中液态水的密度/（kg/m3）；ρg为香菇孔隙中空气的密度/（kg/m3）；φs,0为初始时刻香菇中固体基质的体积分数/%；φw,0为初始时刻香菇中液态水的体积分数/%；λs为香菇固体基质的导热系数/（W/（m·℃））；λw为香菇中液态水的导热系数/（W/（m·℃））；λg为香菇孔隙中空气的导热系数/（W/（m·℃））；Cp,s为香菇固体基质的比热容/（J/（kg·℃））；Cp,w为香菇中液态水的比热容/（J/（kg·℃））；Cp,g为香菇孔隙中空气的比热容/（J/（kg·℃））。物性参数的具体值如表4所示[34]。

表4 物料-干燥箱一体化模型的物性参数Table 4 Physical parameters adopted in the model of material-drying oven integration

2.3.5 模型求解

本试验采用商业软件FLUENT对所建模型进行瞬态模拟求解。非稳态项、对流项分别采用一阶隐式格式、二阶迎风格式进行离散，采用SIMPLE算法进行求解。压力和速度的亚松弛系数分别为0.3和0.7，湍动能和比耗散率的亚松弛系数为0.8，温度的亚松弛系数为1.0。总模拟的干燥时间为14 h，时间步长设置为6 s。

3 结果与分析

3.1 模拟结果与试验数据对比

首先，进行一组进口空气温度为55 ℃、相对湿度为0.35、风速为2 m/s条件下的验证实验，将数值模拟结果与干燥箱内第一层上不同位置香菇的水分比实际变化情况进行对比，结果如图5所示。可以看出，试验数据和模拟结吻合度较高，相对偏差很小。为了更加准确地描述二者之间的微小偏差，计算了模拟结果与试验数据的R2，第1、5、9列的R2分别为0.995 6、0.998 3和0.998 6，3 个不同位置香菇水分比的R2都大于0.99，说明本研究所提出的模拟方法能够用于准确模拟香菇的热风干燥过程。

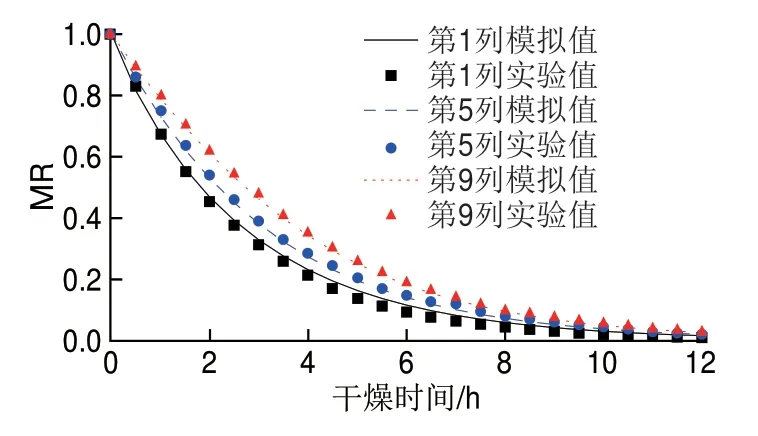
图5 第一层上不同位置香菇的水分比模拟值与实际值的对比结果Fig.5 Comparison between simulated and actual values of moisture ratios at different locations on the first layer

3.2 模拟结果分析

本试验对进口空气温度为55 ℃、相对湿度为0.35、风速2 m/s下的模拟结果展开研究，主要分析香菇干燥过程中的干燥不均匀性，包括干燥过程中不同层、不同列、不同行之间的水分比分布情况。考虑到物理模型在Z轴方向上的对称性，所以只对干燥箱下半部分的第1、3、6层的模拟结果进行分析。

3.2.1 整体的干燥不均匀性

图6给出了不同干燥时期香菇的水分比分布情况。根据水分比的大小分布，将干燥过程分为干燥前期、干燥中期、干燥后期和干燥末期4 个阶段。从图6可以看出，干燥前期的干燥不均匀性最为显著，随着干燥过程的进行，干燥不均匀性逐渐降低。

图6 干燥过程中香菇水分比分布的变化Fig.6 Variation in moisture ratio distribution of Lentinus edodes during drying

在X轴方向即空气流动方向上，干燥前期和中期香菇的干燥不均匀性比较显著，水分比呈现逐渐增大的规律。这主要是因为随着对流换热过程的进行，空气的热量不断向香菇传递，使得空气的温度下降，同时香菇干燥后产生的水蒸气使得空气的相对湿度逐渐升高，所以在空气流动方向上干燥速率逐渐降低，水分比分布呈现逐渐增大的现象。而在干燥后期和末期，香菇的干燥不均匀性逐渐减小，且水分比呈现先增大后减小的分布规律。水分比先增大的原因与干燥前、中期水分比逐渐增大的原因一致，而后逐渐减小是由于在干燥后期和末期，香菇的体积大幅缩小，香菇间隙变大，结合出口处自由流动区域的体积突然变大，引起尾部香菇间的流速增大，导致尾部香菇干燥速率变快。此外，通过比较不同层香菇的水分比分布可以发现，越靠近干燥箱的顶部或底部，空气流动方向上的干燥不均匀性越大。

从图6中还可以看出，在Y轴方向即横向方向上，两侧的水分比明显高于中间位置。这是由于在两侧的位置靠近干燥箱壁面，干燥架与两侧壁面之间空气的自由流动区域体积较大，导致大部分热空气流过自由流动区域，使得流过两侧香菇的热空气流速较小，同时，缓慢的空气流动使得这一区域的空气温度更低，相对湿度更高，所以两侧香菇的干燥速率降低，水分比高于中间位置。随着干燥过程的进行，横向方向上空气的温度和相对湿度的不均匀性逐渐减小，但流速的不均匀性依然存在，所以即使在干燥后期和末期，横向方向上的干燥不均匀性依然较大。此外，通过比较不同层香菇的水分比分布可以发现，越靠近干燥箱中间层，横向方向上的干燥不均匀性越大。

综上，干燥过程中香菇在空气流动方向上和横向方向上都存在明显的干燥不均匀性。在空气流动方向上，越靠近干燥箱顶部或底部干燥不均匀性越明显；在横向方向上，越靠近干燥箱中间层干燥不均匀性越明显。

3.2.2 空气流动方向上的干燥不均匀性

为了更加准确地描述香菇在空气流动方向上的干燥不均匀性，选取第1、3、6层上的第1、3、5、7、9列香菇，并计算出不同时刻每列13 个香菇的水分比平均值，得到变化结果如图7所示。每一层上不同列的香菇具有明显的干燥不均匀性，其中第1层上不同列的香菇水分比差异最大，最大水分比偏差为0.16。另外，根据GB 7096—2014[19]的规定，香菇的水分比为0.026时达到贮存要求，视为干燥过程完成。根据此标准，由图7可以得到第1、3、6层上不同列香菇达到干燥要求的最长时间差值分别为1.42、0.89、0.57 h。

图7 干燥过程中空气流动方向上不同位置香菇水分比的变化情况Fig.7 Variation in moisture ratios of Lentinus edodes in the direction of air flow at different positions during drying

图8、9、10分别为不同层上不同列风速、空气相对湿度和空气温度随干燥过程的变化情况。可以看出，靠近干燥箱出口的第9列区域空气相对湿度较高（图9）、温度较低（图10），但由于风速较大（图8），第9列香菇的干燥速率并没有明显降低，和第7列相差不多（图7）。这一现象在第3层和第6层更加明显，所以空气流动方向上这两层上香菇的干燥结果比第1层更为均匀。结合图7可以看出，在干燥末期阶段，最晚达到干燥要求的是第3列，而不是更加靠近出口的第7或第9列，这主要是因为干燥末期空气的相对湿度和温度趋于一致，而第3列的风速最小，导致其干燥速率降低，最晚达到干燥要求。

图8 干燥过程中空气流动方向上不同位置风速的变化情况Fig.8 Variation in air flow rate in the direction of air flow at different positions during drying

图9 干燥过程中空气流动方向上不同位置空气相对湿度的变化情况Fig.9 Variation in air relative humidity in the direction of air flow at different positions during drying

图10 干燥过程中空气流动方向上不同位置空气温度的变化情况Fig.10 Variation in air temperature in the direction of air flow at different positions during drying

3.2.3 横向方向上的干燥不均匀性

在横向方向上，同样对第1、3、6层上的香菇进行分析，由于在横向方向呈中间对称，所以选取每一层上的第1、3、5、7行进行研究。首先计算出不同层上每一行9 个香菇的水分比取平均值，得到水分比变化结果，如图11所示。在相同时刻，同一层上越靠近边侧香菇的水分比越高，其中第1行香菇的水分比明显高于其余几行，这与3.2.1节中的分析结果一致。对比不同层上的水分比变化可以发现，越靠近干燥箱中间层，不同行的水分比差异越大，最大水分比偏差出现在第6层上，差值为0.08。另外，由图11可以得到，第1、3、6层上不同行香菇达到干燥要求的最大时间差值分别为1.16、1.24、1.35 h。

图11 干燥过程中横向方向上不同位置香菇水分比的变化情况Fig.11 Variation in moisture ratios in the horizontal direction at different positions during drying

图12、13、14分别给出了不同层上不同行的风速、空气相对湿度和空气温度随干燥过程的变化情况。可以看出，在同一层上越靠近中间位置，空气的流速和温度越高，空气的相对湿度越低，所以同一层上越靠近中间位置，香菇的水分比越低。从图中还可以发现，越靠近干燥箱中间层，在横向方向上流速偏差越大，最大偏差达到0.28 m/s，导致越靠近干燥箱中间层香菇的干燥不均匀性越大。

图12 干燥过程中横向方向上不同位置风速的变化情况Fig.12 Variation in air flow rate in the horizontal direction at different positions during drying

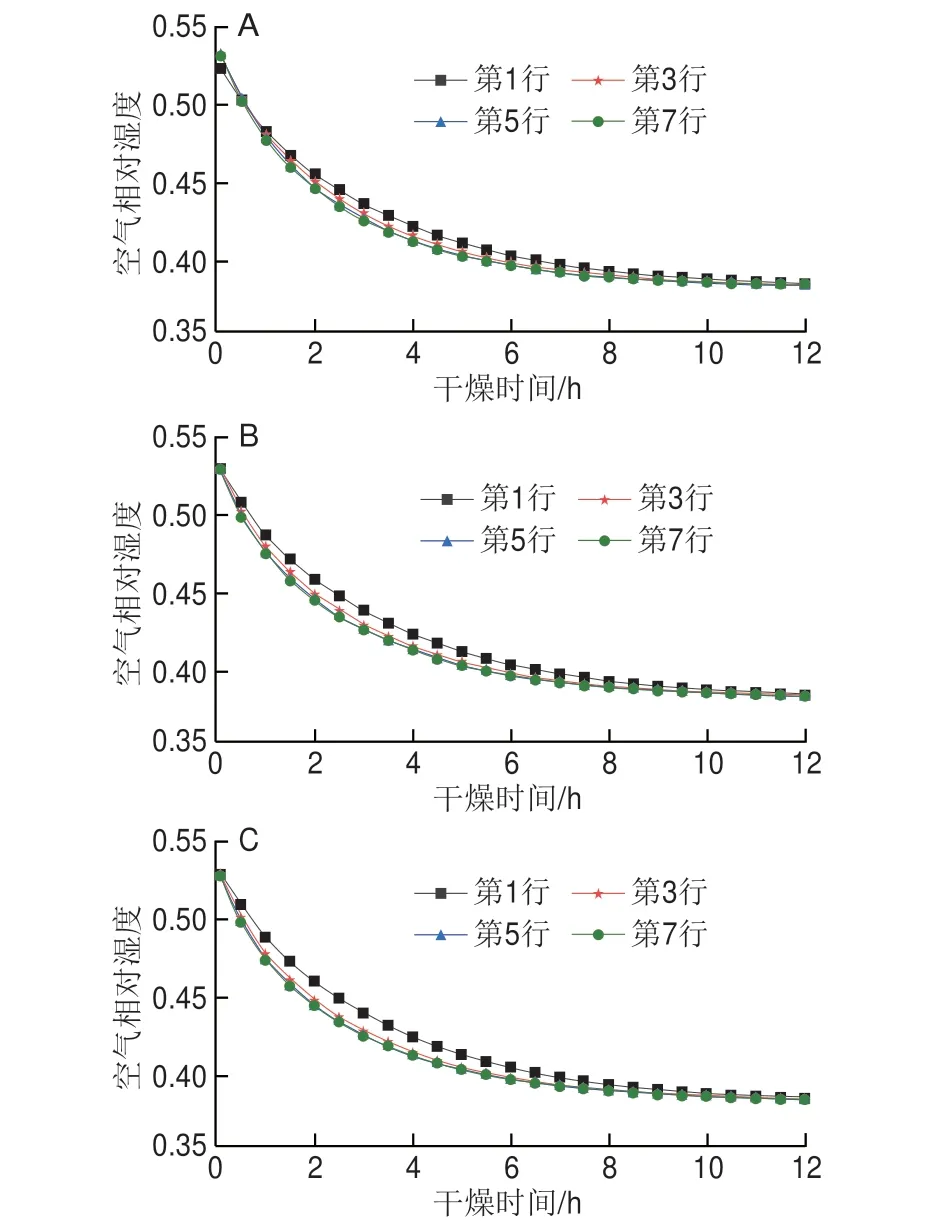
图13 干燥过程中横向方向上不同位置空气相对湿度的变化情况Fig.13 Variation in air relative humidity in the horizontal direction at different positions during drying

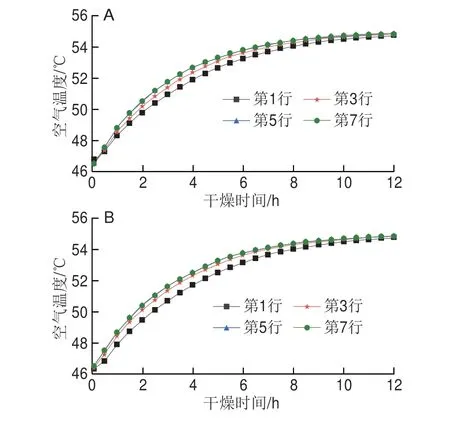
图14 干燥过程中横向方向上不同位置空气温度的变化情况Fig.14 Variation in air temperature in the horizontal direction at different positions during drying

4 结 论

本实验以香菇为研究对象，开发了物料与干燥箱一体化的热风干燥数值模拟方法，并通过实验验证了模拟方法的精确度，能够用于准确模拟大批量的香菇热风干燥过程。通过分析该方法的模拟结果得出以下结论：1）干燥过程中，整体存在明显的干燥不均匀性，在干燥前期干燥不均匀性最为显著，随着干燥的进行，不均匀程度逐渐降低；2）在空气流动方向上，越靠近干燥箱顶部或底部干燥不均匀性越明显，同一层上达到干燥要求的最大时间偏差为1.42 h；3）在横向方向上，越靠近干燥箱中部干燥不均匀性越明显，达到干燥要求时的最大干燥时间偏差出现在第一层，为1.16 h。本研究所开发的香菇热风干燥模拟方法可用于干燥工艺优化、干燥箱结构设计和产品质量提升等方面，可为香菇热风干燥技术的进一步发展提供支撑。