基于热循环曲线法的低合金高强钢对接接头焊接残余应力数值模拟

廖 娟,程 鹏,冯 芳,蒋 鸿

(1.西南交通大学希望学院,成都 610400;2.国网四川省电力公司成都供电公司,成都 610041)

0 引 言

低合金高强钢具有综合性能优异和成本低的优点,多用于重要的焊接结构,在石油工程、火力发电、工程机械等诸多领域得到广泛的应用。在焊接过程中低合金高强钢会发生固态相变,这会明显改变结构的应力和应变,从而造成结构变形[1]。同时,焊接残余应力也会显著影响结构的疲劳强度和应力腐蚀开裂行为,而且残余拉应力是促使结构发生脆性断裂的重要因素。因此,研究低合金高强钢焊接件的残余应力具有重要的理论意义和工程应用价值。

由于现场实地测试结构件残余应力的成本高、工作量大,近年来,数值模拟方法在此方面的应用取得了很大的进展。针对钢结构焊接残余应力的有限元模拟,国内外学者已做过很多研究:陆皓等[2]采用考虑组织演变的温度-组织-应力耦合计算了低合金高强钢焊接残余应力;LEE等[3-4]研究了高强钢相变对环焊缝和厚板多道焊对接接头残余应力的影响;马学周[5]研究了高强钢不同接头形式多层多道焊接头残余应力的分布。以上研究预测精确,但计算过程耗时长,影响实际工程应用的模拟周期。GOLDAK 等[6]提出的三维双椭球体热源(3Ddouble ellipsoidal heat source,3D-DEHS)模型已广泛应用于焊接数值模拟,大量研究成果验证了其用于模拟弧焊温度场的准确性,但计算效率不高[7]。为了提高计算效率,CAI等[8]提出了串热源模型,但需要采用细小网格对焊接残余应力进行计算;HU等[9]研究了二维实体模型对焊接残余应力计算精度和效率的影响;PERI'C等[10]采用二维和三维单元混用的实体模型模拟焊接残余应力,发现混用模型能提高计算效率,但会降低计算精度。采用热循环曲线(thermalcyclecurve,TCC)对热源模型进行简化可提高数值模拟的计算效率[11]。为了兼顾计算精度和计算效率,采用三维实体模型保证模拟精度的同时,结合基于TCC的热源模型提高计算效率的焊接残余应力模拟方法研究相对匮乏。

为此,作者采用SYSWELD软件建立了低合金高强钢Q345对接接头单道焊和2层3道焊的热-冶金-力学三维耦合计算模型,在考虑相变情况下,采用三维双椭球体热源模型计算了单道焊温度场,再基于TCC对该热源模型进行简化,并将温度场模拟结果与试验结果进行对比;分别采用三维双椭球体热源模型和基于TCC简化的热源模型对单道焊和多道焊对接接头的残余应力分布进行计算,并进行了试验验证。研究结果对于提高复杂焊接结构的模拟效率具有实际工程意义。

1 试样制备与试验方法

焊接用母材为尺寸200 mm×150 mm×10 mm 的Q345热轧钢板,化学成分如表1所示。采用AVP-360 型交直流两用脉冲TIG 焊机对Q345钢板进行单道惰性气体钨极保护(TIG)对接重熔焊接,不开坡口,焊接电流为200 A,焊接电压为12.5 V,焊接速度为10 cm·min-1,保护气体为纯度99.99%氩气。

表1 Q345钢的化学成分Table 1 Chemical composition of Q345 steel

焊接完成后,在接头上以焊缝为中心垂直于焊缝方向截取金相试样,经打磨、抛光,用体积分数4%硝酸酒精溶液腐蚀后,采用Axio Vert.A1 MAT型倒置数字材料显微镜观察接头形貌。采用TLWELD热电偶丝碰焊机将K 型热电偶一端点焊到测试点,另一端接入GL220型焊接热循环曲线测试仪,记录温度随时间的变化曲线。参考文献[12-13],采用盲孔法测定钢板上表面中心位置的纵向和横向残余应力。

2 焊接模型的建立

2.1 网格划分和材料的热物性参数

为了准确模拟焊接过程中接头的温度场和应力场,采用三维实体计算模型。在建立TIG重熔焊接Q345钢的有限元模型时,采用visual-mesh划分网格,模型的节点数为66 303,单元数为61 568,最小单元尺寸为1.56 mm×1 mm×0.63 mm。为了兼顾计算精度和效率,焊缝及近缝区采用较细的网格,远离焊缝区采用较粗大的网格。模拟过程中采用三点约束以防止模型发生刚体位移。具体的有限元模型如图1所示,图1中箭头方向为焊接方向,Line1为钢板上表面中心位置。假定焊缝金属与母材Q345钢具有相同的热物理性能和力学性能,性能参数取自参考文献[14]。

图1 TIG重熔焊接Q345钢的有限元模型Fig.1 Finite element model of TIG remelting welding Q345 steel

2.2 热源模型及边界条件

对于单面对接焊接,热源采用三维双椭球体热源模型,热源移动方向为y轴方向,该体热源由y轴前后2个部分组成。y轴前半部分和后半部分的椭球内部热流密度分布函数qf,qr表达式[15]分别为

式中:af,ar,b,c均为热源形状参数;Q为有效热输入;ff,fr分别为热流密度在y轴前后2个部分的分配系数。

设置焊件初始温度为20℃,焊件表面与周围介质的热交换为表面换热,将对流和辐射系数转化为总热交换系数来进行模拟计算。

2.3 力学模型

在焊接过程中,温度场随时间的变化会引起热应变和相变应变。假定材料遵循各向同性的弹塑性准则(von Mises塑性模型),则总应变速率增量ε·可表示为

式中:ε·E,ε·P,ε·T,ε·TP,ε·C分别为弹性应变速率、塑性应变速率、热应变速率、相变塑性应变速率和蠕变应变速率。

在采用增量有限元分析法进行模拟时,ε·E可根据胡克定律由弹性模量和泊松比计算得到,ε·T可由热膨胀系数计算得到,ε·P可由von Mises屈服准则和各向同性硬化规律计算得到,ε·TP可用相变塑性系数计算得到[16-17];焊接是短时间的加热和冷却过程,在高温停留时间较短,可忽略ε·C的影响[15]。

3 温度场模拟与基于TCC简化热源模型的建立

3.1 焊接温度场模拟结果与试验验证

由图2可知:在单道焊焊接模拟过程中,熔池中心最高温度为1 963℃,温度达到1 450℃的区域为熔化区;模拟得到熔池深度最大处焊缝截面熔化区和热影响区的形状和尺寸与试验得到的焊缝和热影响区的形状和尺寸吻合。

图2 模拟得到熔池深度最大处的单道焊接头焊缝截面温度分布以及试验得到的接头形貌Fig.2 Temperature distribution of weld cross section of singlepass welded joint at maximum pool depth by simulation(a)and joint morphology by test(b)

图3为单焊道焊缝截面A、B点的热循环曲线模拟结果与试验结果,其中A、B点距熔池边缘距离分别为1,3 mm。由图3可知,不同位置的热循环曲线模拟结果与试验结果吻合良好,相对误差小于2.34%,验证了所提取的热循环曲线的准确性。

图3 单道焊接头焊缝截面不同位置的热循环曲线模拟结果与试验结果Fig.3 Simulation and test results of thermal cycle curves of different positions on weld cross section of single-pass welded joint

3.2 基于TCC简化热源模型的建立

通过单道焊温度场模拟结果,提取焊缝截面上熔化区中所有节点的热循环曲线,并求出平均值,得到一条新的热循环曲线作为热源,结果如图4所示。在模拟焊接过程中,焊缝中所有节点同时受到该热源作用,经历焊接的加热和冷却过程,热源的加载时间为0～270 s,270 s时焊件温度降至约100℃,之后不再施加热循环曲线,焊件自然冷却到室温。

图4 基于TCC简化的热源模型的温度与时间关系曲线Fig.4 Temperature-time curve of heat source model simplied by TCC

4 焊接残余应力模拟结果及分析

4.1 单道焊焊接残余应力

图5为单道焊接头上表面Line1处的纵向和横向残余应力分布模拟结果和试验结果。由图5可以看出:在焊缝及近焊缝区为拉应力,远离焊缝区为压应力。这是由于焊接加热过程中,随着温度的升高,材料膨胀受阻产生压应力,当温度达到熔点时,应力降为0;冷却时焊缝及热影响区受到周围母材的约束,焊缝区域拉应力急剧升高,冷却到室温时焊缝及近缝区产生拉应力,为了保证整个焊件受力平衡,远离焊缝区为压应力。纵向残余应力的峰值出现在焊缝中心,采用三维双椭球体热源模型和基于TCC简化的热源模型模拟得到单道焊接头焊缝区的纵向残余应力模拟结果与试验结果吻合良好,相对误差分别小于11.38%,4.34%。采用基于TCC简化的热源模型模拟得到的最大纵向残余拉应力为571 MPa,大于采用三维双椭球体热源模型模拟得到的485 MPa。主要原因是用三维双椭球体热源模型模拟时,焊缝中心某点在热源中心到达前受到热源前端的热输入影响,在热源中心离开时受到热源后端热输入影响,而用基于TCC简化的热源模型模拟时,整条焊缝同时经过相同的加热过程,忽略了焊接方向上热源前端和后端的热流分布差异,低估了电弧热作用时间[18],因此模拟得到的空间温度梯度更高,焊接残余应力更大[19]。采用基于TCC简化的热源模型模拟得到的焊缝及近缝区拉应力范围稍大于采用三维双椭球体热源模型模拟得到的拉应力范围。这是由于基于TCC简化的热源模型的热源长度大于三维双椭球体热源模型,模拟时热源在板宽方向的传热更快,在焊接线垂直方向超过某一峰值温度的区域会更大,由此产生的塑性变形区也更大[20]。三维双椭球体热源模型和基于TCC简化的热源模型模拟得到的单道焊接头的横向残余应力分布趋势相似。横向残余应力的峰值出现在焊缝中心,采用基于TCC简化的热源模型模拟得到的最大横向残余拉应力为250 MPa,大于采用三维双椭球体热源模型模拟得到的212 MPa。焊缝中心到热影响区的横向残余应力先减小后增大,远离焊缝区的应力逐渐减小并趋于0。横向残余应力产生的原因复杂,其值受到焊缝冷却时横向收缩的直接影响,同时受到焊缝的纵向收缩、表面和内部不同冷却过程以及叠加的相变过程共同作用的间接影响[16]。横向残余应力的数值小于纵向残余应力的数值,这是由于在焊缝冷却收缩与相变膨胀过程中钢板的纵向拘束远大于横向拘束。采用基于TCC简化的热源模型和三维双椭球体热源模型模拟时的计算时长分别为103,155 min,可见基于TCC简化的热源模型的计算效率提高约32%。

4.2 多道焊焊接残余应力

图6为采用三维双椭球体热源模型和基于TCC简化的热源模型模拟得到的多道焊接头残余应力分布,焊接时采用V型坡口,分2层进行焊接,共3道焊缝。由图6可以看出:3道焊接头纵向残余应力在焊缝及近焊缝区为拉应力,峰值区域主要分布于焊道2、焊道3的接触区域及焊道2的热影响区附近,采用基于TCC简化的热源模型和三维双椭球体热源模型模拟得到的最大纵向残余拉应力分别为820,769 MPa,相差51 MPa;热影响区靠近母材处应力骤减,远离焊缝区为压应力。3道焊接头横向残余应力几乎为拉应力,焊缝中心到热影响区应力逐渐增大,远离焊缝区的应力逐渐减小并趋于0;采用基于TCC简化的热源模型和三维双椭球体热源模型模拟得到的最大横向残余拉应力分别为247,245 MPa,仅相差2 MPa。对比可知,2种热源模型模拟得到的残余应力分布基本一致,最大残余应力均位于焊道2的热影响区近母材附近,由于第3道焊缝的焊接使第2道焊缝的部分金属熔化或软化,缓解了焊道2的残余应力峰值,因此焊道2和焊道3交界处的应力峰值略低于焊道2的热影响区近母材侧的应力峰值。基于TCC简化的热源模型和三维双椭球体热源模型模拟时的计算时长分别8,15.5 h,可见基于TCC简化的热源模型的计算效率提高约50%。

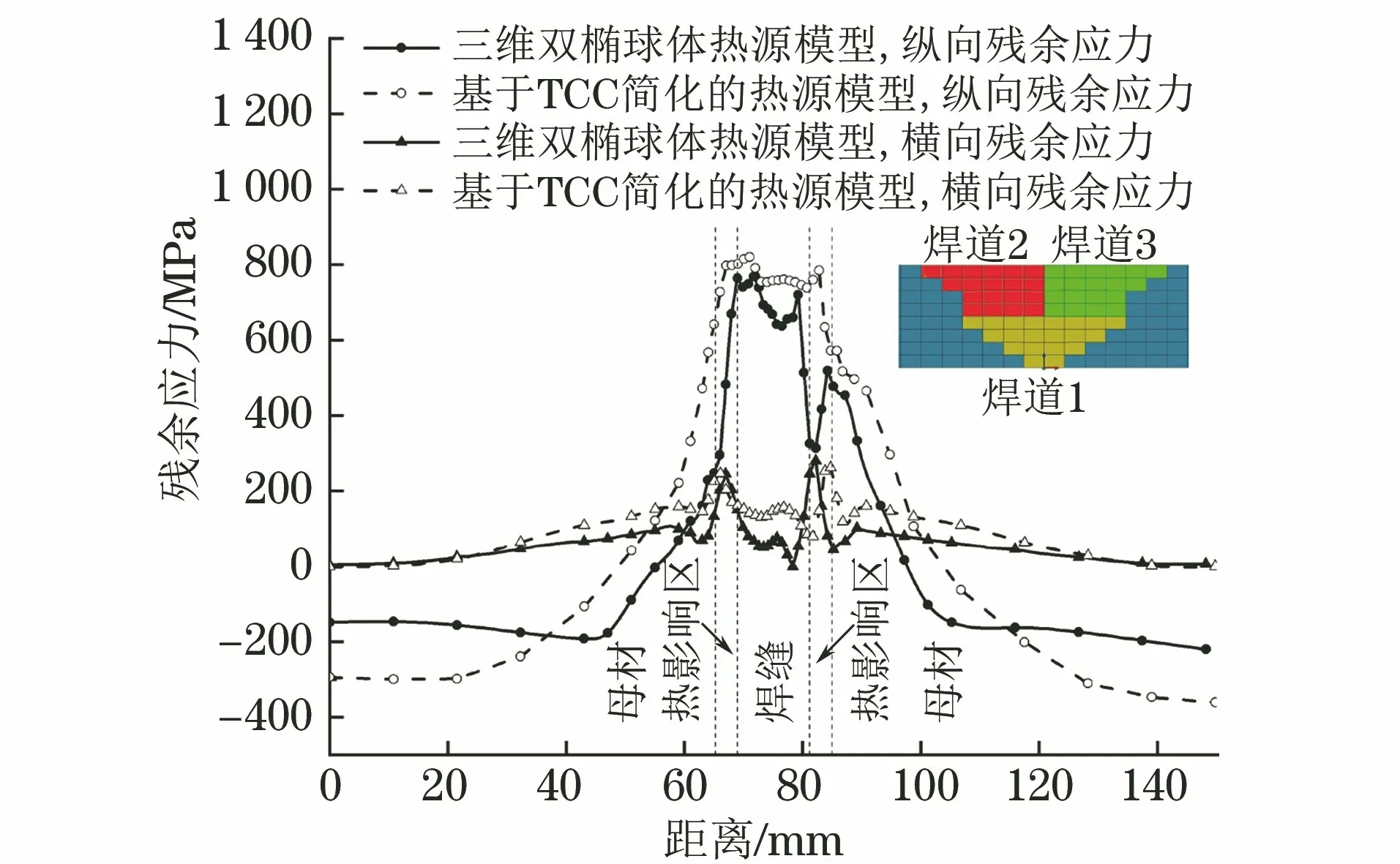
图6 不同热源模型模拟得到多道焊接头残余应力分布Fig.6 Residual stress distribution of multi-pass welding welded joint simulated by different heat source models

5 结 论

(1) 由单道焊温度场模拟得到,熔池深度最大处焊缝截面熔化区和热影响区的形状和尺寸与试验得到的焊缝和热影响区的形状和尺寸吻合;根据温度场模拟结果提取的不同位置的热循环曲线模拟结果与试验结果吻合良好,相对误差小于2.34%,验证了热循环曲线的准确性。

(2) 单道焊接头的残余应力峰值出现在焊缝中心,采用三维双椭球体热源模型和基于TCC简化的热源模型模拟得到焊缝区的残余应力模拟结果与试验结果吻合良好,纵向残余应力相对误差分别小于11.38%,4.34%,横向残余应力分布趋势相似,验证了2种模拟方法的准确性;与三维双椭球体热源模型相比,基于TCC简化的热源模型的计算效率提高约32%。

(3) 采用三维双椭球体热源模型和基于TCC简化的热源模型模拟得到的多道焊接头残余应力分布基本一致,最大纵向残余拉应力分别为820,769 MPa,最大横向残余拉应力分别为247,245 MPa;与三维双椭球体热源模型相比,基于TCC简化的热源模型的计算效率提高约50%。