金属铸锭自动扒渣过程流体仿真研究

杨公波,杜 磊,黄文虎

(长沙有色冶金设计研究院有限公司,湖南 长沙 410000)

0 引言

目前,国内电锌生产过程中劳动强度最大的铸锭、堆垛、排板和制片等操作工序早已被自动化装备取代,但锭面扒渣仍采用人工作业方式[1],该工序的工作条件恶劣。

1)环境温度高,铸模上方最高达500 ℃以上,烟尘重;

2)高温熔液遇水汽易发生爆炸飞溅,对扒氧化皮操作人员有烫伤的危险;

3)劳动强度大,操作人员在铸模旁弯腰作业,每8 s 需完成一次扒渣、抛渣、清铲、返回等动作。目前,冶炼厂在该环节的人力成本也逐年递增;

4)浇注现场存在从高温铸模中逸出的铅蒸气,扒氧化皮作业人员长期近距离接近铅液,铅蒸气经呼吸道和皮肤进入人体,是造成铅中毒职业病的原因之一。

因此,采用机器人自动扒渣取代人工成为大势所趋,但目前对于扒渣装置的最佳结构及工作参数的研究尚少。本文旨在研究扒铲的浸入深度、运行速度、倾斜角度等影响因素对扒渣效果以及对锭模内流体运动的影响,从而为扒铲的结构和工作参数设计提供借鉴。

扒铲的主要工作分为扒渣和捞渣,扒渣过程是将锭模中渣皮聚集起来,捞渣过程将聚集起来的渣皮从锭模中捞出。扒渣过程近似于匀速运动,而在运动至扒渣过程的行程终点时,扒铲会在前进的同时向下运动,再向前运动至与扒渣槽内壁接触,然后沿着内壁将渣皮缓缓捞出[2]。

扒渣过程可以通过Fluent 软件做流体仿真,在建立扒铲扒渣过程的模型后,改变扒铲的运行速度、浸入深度、倾斜角度,分析上述因素对扒渣效果以及对锭模内流体运动的影响,从而为扒铲工作参数设计提供借鉴。

利用Fluent 软件进行扒铲的扒渣过程流体仿真研究,需要进行以下三部分工作[3]。

首先,建立扒渣过程的数值模拟模型,模型主要包含了锭模、扒铲以及锌液。在建立仿真模型时,需要确立锭模及扒铲主要尺寸,并根据实际情况对其进行合理的条件假设和模型简化,方便仿真计算。在建立仿真模型后,需要将其网格划分,为研究计算做准备。

然后,对锌液及其氧化物在扒铲作用下的流动状态进行仿真研究。使用流体仿真为了研究锌液在锌盘中的流动状态,锌液表面及其氧化物在不同几何尺寸、形貌特征、表面状态、运动位置状态的扒铲作用下的流动状态提供依据。因此,仿真需要完成对数值模拟模型中的参数以及初始条件的设置,并运用控制变量的研究方法,分别改变扒铲的浸入深度、运行速度、倾斜角度等影响因素,完成多组对比仿真实验。

最后,根据多组对比实验结果,分析以上因素对扒铲除渣效果和平稳性的影响,确定能使扒铲除渣效果和平稳性较好的影响因素范围,进而对扒铲的结构设计提出改进方案。

1 仿真模型建立

1.1 物理几何模型

锭模上表面尺寸为422 mm×220 mm,下表面尺寸为396 mm ×170 mm,整体高度为50 mm,扒铲的宽度与锭模宽度一致,设置为422 mm,扒铲的初始厚度设置为5 mm。氧化锌渣皮简化为浮在锌液上厚度为1 mm 的流体。

为了简化模型且优化仿真计算,根据工业实际情况,假设锌液为不可压缩流体;不考虑铸模底和模壁的厚度;由于扒渣时间比较短,不考虑温度降低对扒渣过程的影响。

1.2 网格划分

使用ANSYS 中的ICEM 软件进行网格划分,使用非结构网格划分整个锭模模型,采用四面体单元,总网格数大约为120 万个左右。为了简化网格模型,扒铲在锭模上表面以外部分被去除,且锭模内部部分被简化为一个空腔,锭模网格模型如图1 所示。

图1 锭模网格模型图

1.3 模型参数设置

在流体仿真模型中,需要提前设置材料参数、边界条件、初始条件、物理模型以及求解器和操作条件等等。

1)材料参数定义

在建立数学模型中非常重要的一步是正确设定所研究对象的材料参数,锭模中液体主要分为下层大部分的锌液和上层小部分的锌渣,锌液的化学成分为Zn,锌渣是锌液与空气的氧气发生反应所产生的ZnO。其各自的物理特性参数如表1所示[4]。

表1 锌液与锌渣物理特性参数

2)边界条件设置

边界条件就是流场变量在计算边界上应该满足的数学物理条件。边界条件与初始条件一起并称为定解条件,只有在边界条件和初始条件确定后,流场的解才存在,并且是唯一的,所以边界条件对求解结果有非常大的影响,因此要合理准确的设置好边界条件。

运动边界条件:锭模的侧壁以及底面采用静止壁面条件;扒铲采用动网格设定其边界条件,为运动刚体,其运动速度定为0.09 m/s。

压强边界条件:由于锌液上方有空气存在,所以锭模上表面设定为压强入口条件,大小为一个标准大气压。

3)初始条件设置

选择Standard Initialization 对流场进行初始化,对压强、速度、湍流变量、第一相组分体积分数进行设定,完成全局初始化。由于在本次研究中使用了动网格设置,因此在全局初始化过程中不需要设置运行速度,并且设置第二、三相组分体积分数为0。

在完成了全局初始化后,利用Patch 功能,即修补功能,对局部区域内变量的值进行修改,进行局部初始化,补充其他相的体积分数,完成对流场初始条件的全部设定,即将不同流体补充到划分好的区域。

4)基本物理模型选取

由于将氧化锌渣皮假定为了一种流体,所以应在锭模中建立出锌液流体和氧化锌渣皮的模型,因此选择多相流模型。而Fluent 提供了四种多相流模型:VOF(Volume of Fluid)模型、Mixture(混合)模型、Eulerian(欧拉)模型和Wet Steam(湿蒸汽)模型。一般常用的是前三种模型,Wet Steam 模型只有在求解类型是Density-Based 时才激活。由于VOF模型的主要研究对象是分层流,而混合模型和欧拉模型的主要研究对象是混合流体,因此在本研究中选取VOF 模型作为基础模型,选择显性方式并打开体积力增强选项(Implicit Body Force),用以提高收敛精度,然后在Phase 面板中设定好主相与次相的材料。

由于扒铲在运动时会引起锌液湍流运动,所以选择k-ε双方程湍流模型,使用标准壁面函数;模型常数均采用系统默认值。

5)求解器和操作条件设置

求解器类型分为两种:Pressure-Based 和Density-Based。Pressure-Based 是基于压力法的求解器,使用压力修正算法,擅长求解不可压缩流动,对于可压流动也可以求解。Density-Based 是基于密度法的求解器,具有比较好的求解可压缩流动能力。由于锌液被假定为不可压缩流体,所以选取Pressure-Based 求解器。

由于在计算中要考虑重力的影响,所以需要确定重力的数值和方向,并设置好参考压力值的大小以及参考压力值的位置。

1.4 模拟结果

在流体仿真模型中,需要提前设置材料参数、边界条件、初始条件、物理模型以及求解器和操作条件等等。

在确定好初始条件参数之后,进行扒铲的扒渣过程流体仿真,模拟出来的锌液流场与实际工业生产情况进行对比分析,验证模拟的准确性。模拟结果如图2、图3 所示。

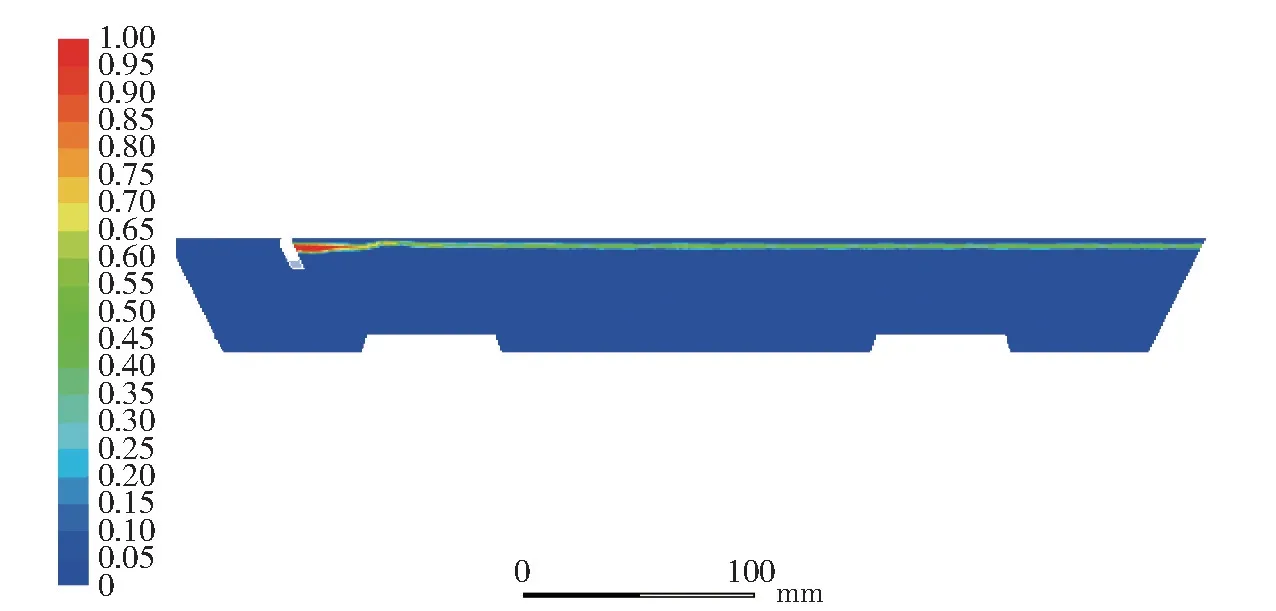
图2 扒铲扒渣运动初始阶段z=0 截面上的渣皮体积分布图

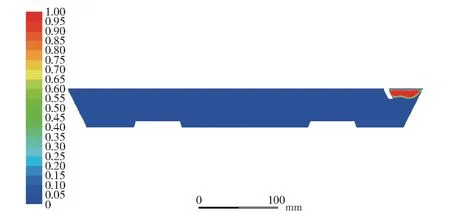
图3 扒铲扒渣结束运动阶段z=0 截面上的渣皮体积分布图

根据模拟出来的氧化锌体积分布图可以看出,扒铲在扒渣过程的初始阶段,锌渣均匀浮在锌液表面,随着铲子的匀速移动,锌渣不断积累,靠近扒铲的部分锌渣厚度不断增加。在扒铲扒渣过程结束时,锌渣累积在锌槽的另一端,没有下沉趋势,保持着上浮的稳定状态。

从模拟出来的氧化锌渣皮体积分布图可以看出,当快运行至行程终点时,锌渣被完全集中在锭模左侧,这与实际工作情况要求大致相符,因此该流体仿真模型是可行的。

另外,根据扒铲扒渣运动的速度矢量图,可以推断扒渣过程的流场状态。扒铲扒渣运动初始阶段z=0 截面上的速度矢量图如图4 所示。

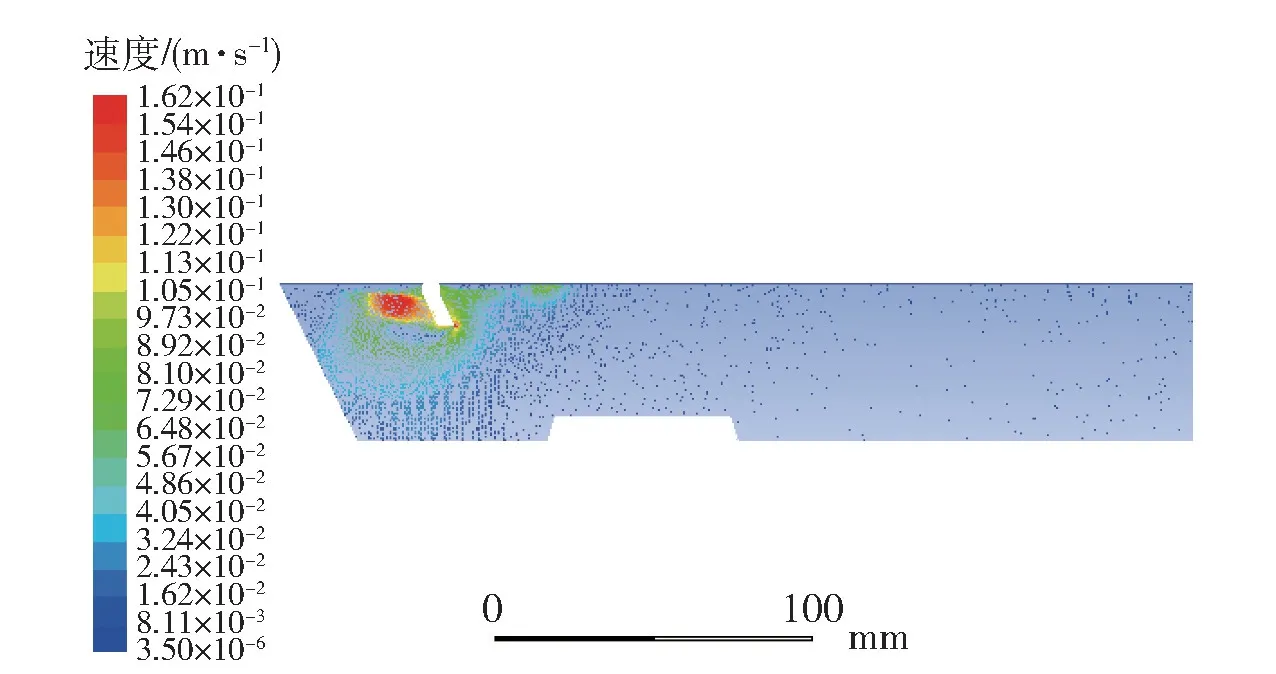
图4 扒铲扒渣运动初始阶段z=0 截面上的速度矢量图

从图4 来看,可以发现扒铲左右两侧的锌液都向右流动且扒铲左侧锌液流速明显比右侧大,即比扒铲运动速度大。这是由于当扒铲进行扒渣运动时,在短暂时间内会使扒铲左右两侧液面高度不一致,右侧液面会明显高于左侧液面,而左侧液面低于静止时的液面,在重力的影响下会产生重力势能,迫使锌液流动补充扒铲左侧液面,而补充的锌液来自于扒铲右侧的锌液,这也就是扒铲附近涡流的形成原因,而左侧锌液在扒铲以及涡流的共同作用下速度才会比扒铲右侧锌液流动速度大,不过在扒铲向右的运动过程中,扒铲左右两侧的速度差值会逐渐缩小。因此,锌液的速度和大小也大致符合实际运动情况。

2 扒渣影响因素分析

扒铲的主要影响因素初始值如表2 所示。

表2 影响因素初始值表

2.1 浸入深度对扒渣的影响

在初始浸入深度基础上,每隔1 mm 取一个数值进行模拟。氧化锌渣皮体积分布如图5 所示,速度云图分布如图6 所示。

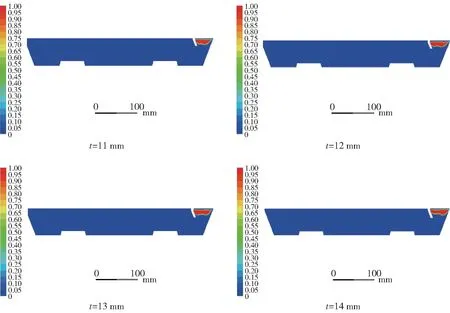
图5 浸入深度不同时z=0 截面上的渣皮体积分布图

图6 浸入深度不同时z=0 截面上的速度云图

由图5 可见,当扒铲浸入深度大于扒渣过程中锌液堆积的最大高度时,增加浸入深度并不影响整体渣皮的流动规律,即在扒铲能够很好地将渣皮聚集起来时,增加扒铲的浸入深度对扒渣效率无影响。

由图6 可见,随着浸入深度的增加,锭模中锌液的运动速度明显增加,这表明增加浸入深度对锭模中锌液的流动有十分显著的影响。而锌液流动越剧烈,越容易与空气反应生成更多的氧化渣,既影响锌锭的外观,也造成金属的浪费。

2.2 运行速度对扒渣的影响

在初始运行速度0.09 m/s 基础上,每减少0.01 m/s 取一个数值进行模拟。运动速度与扒刀表面锌渣堆积厚度关系图如图7 所示。

图7 运动速度与堆积厚度关系图

从图7 可知,随着扒铲速度的增加,渣皮堆积厚度呈上升趋势,不过当速度增大到一定程度时,渣皮堆积厚度会大于扒铲浸入深度,从而导致渣皮从扒铲下方流出,严重影响扒渣质量。

2.3 倾斜角度对扒渣的影响

在初始倾角tanα=0.5 基础上,每隔tanα=0.25 取一个数值进行模拟。由于在某些角度下,渣皮会从扒铲下流出,从而影响锌锭质量以及扒渣效率,因此使用渣皮从扒铲下方流出位置时的运动行程与总行程的比值衡量扒渣效率。

从图8 可知,随着角度的增大,渣皮从扒铲下方流出的现象逐渐减轻,在α=26.6°附近完全消失。此外,改变扒铲倾斜角度对锭模中锌液流动影响不大,主要影响扒铲附近锌液的流动,扒铲倾斜角度越大,扒铲前面流体向前流动的速度也就越大,对流体的影响范围也就越大。

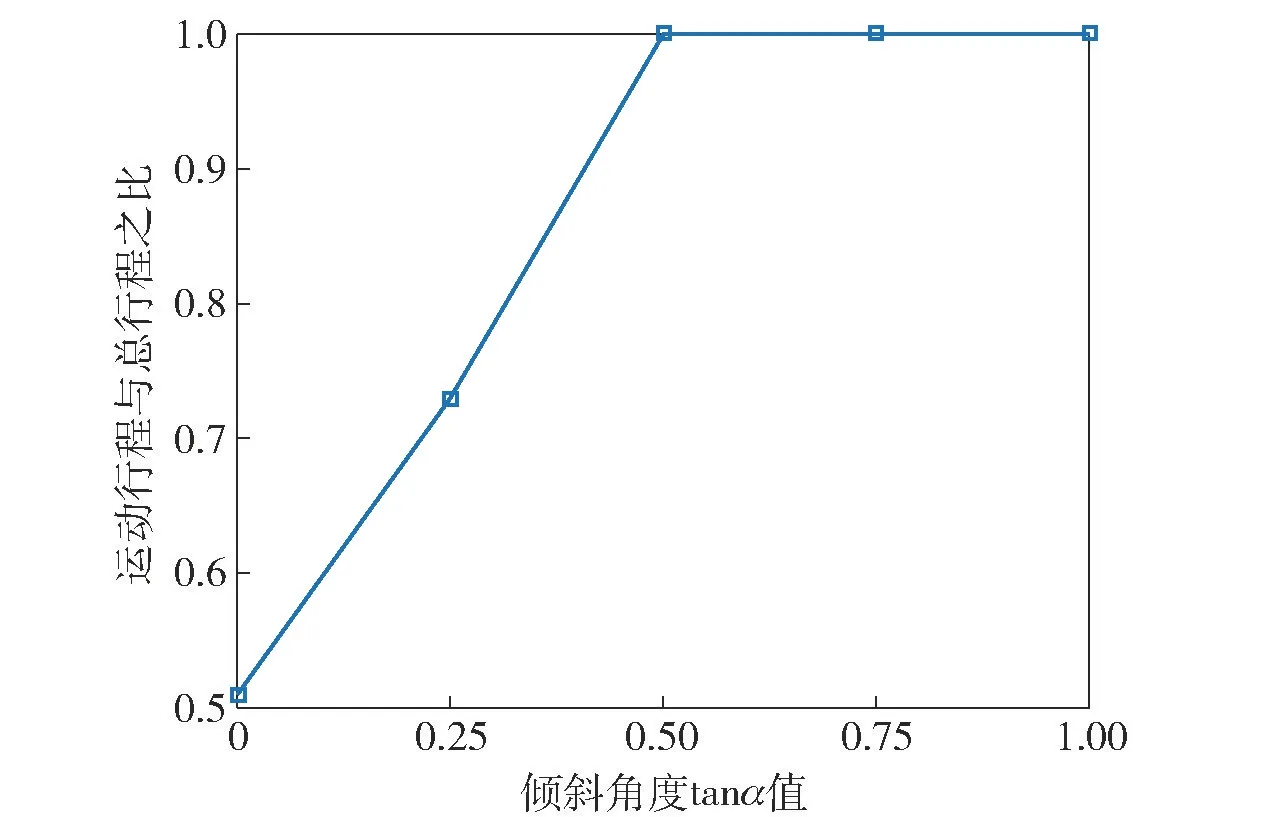
图8 倾斜角度与运动行程与总行程之比

3 结论

通过对仿真结果的分析,得出以下结构。

1)改变扒铲的浸入深度对扒渣过程有影响,尤其在扒铲下方有氧化锌渣皮流出时,增加扒铲浸入深度可以有效阻止此现象,但是随着扒铲浸入深度的增加,锭模内锌液的整体流动速度也会明显增加,即会对锭模内锌液的流动产生显著影响。在尽量提高扒渣合格率(清除锌渣的效率)的前提下,同时减少锌液整体流动的波动性,应选扒铲的浸入深度在10～14 mm 范围内。

2)改变扒铲的运行速度会对扒渣过程有很明显的影响,扒铲运行速度越小,扒渣过程就越稳定,渣皮堆积的厚度也就越小;相应的,扒铲的浸入深度随之减小,对锭模内锌液流动的影响也会减小,并且减小扒铲运动速度本身就能减少对锭模内锌液流动的影响。但是扒渣运行速度太低,会使扒渣整体过程周期变长,需要保证不影响扒渣效率的基础上,控制合适的扒渣运行速度,应选择速度在0.06～0.09 m/s 范围内。

3)改变扒铲的倾斜角度也会对扒铲的扒渣过程产生显著的影响,且随着角度的增大,扒铲将氧化锌渣皮集中的能力也在缓慢增强,但是角度的改变对锭模中锌液流体的流动影响不大,主要影响扒铲运动方向上流体的运动,使其能更快达到与扒铲运动近似的速度,这也是倾角的改变会对扒渣过程产生影响的原因。为保证锭模中锌液流体的流动稳定,应控制扒铲倾斜角度在26°～45°。