“平均数”一二三

吴俤仙

你掌握“平均数”的知识点了吗？随我来看看下面的“一”“二”“三”吧！

一、平均数的意义

通俗来讲，平均数是指用一组数据中所有数据的和除以数据的个数，反映的是這组数据的平均水平。

平均数与以后要学习的众数、中位数不同。众数是指一组数据中出现次数最多的数，反映的是这组数据的众多水平；中位数是把一组数据按从小到大的顺序排列，在中间的一个数（或中间两个数的平均值）反映的是这组数据的中等水平。在5、32、8、5、7、8、5这组数中，平均数是（5+32+8+5+7+8+5）÷7=10；这些数中，5出现了3次，出现的次数最多，所以5是这组数的众数；7是这组数的中位数，因为把这7个数按从小到大的顺序排列，7排在中间。

二、平均数的解法

解答平均数数学问题的方法比较多。在小学阶段，大家要掌握“移多补少”和“直接计算”这两种方法。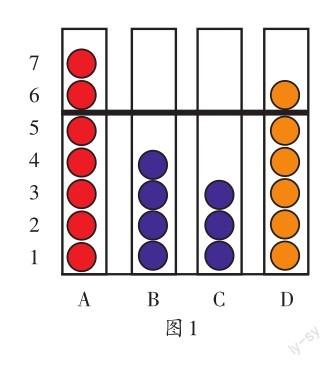

图1中，A、B、C、D四个筒中装了不同数量的球，平均每个筒装了多少个球？从图中可以看出，A筒中有7个球，C筒中有3个球，A筒中比C筒中多4个球。从A筒中“移”出2个到C筒中，A、C两筒中球的数量都变成了5。像这样把多的“移”出来“补”给少的，就叫“移多补少”。同样道理，把D筒中的球“移”1个给B筒，B、D两筒中球的数量也都变成了5。也就是说，A、B、C、D四个筒中原来装了不同数量的球，现在都变成了5个球。5就是平均每个筒装球的数量，即四个筒装球的平均数。

“直接计算”是根据平均数的意义，用所有数据的和除以数据的个数，即总数÷份数=平均数。所以，平均每个筒装球的个数是（7+ 4+3+6）÷4=5（个）。当然，用“移多补少”解决平均数问题有局限性。如果题中的数据不能刚好可以“移”、可以“补”，就不能用这种方法。而用“直接计算”解决平均数问题的方法，具有普遍性。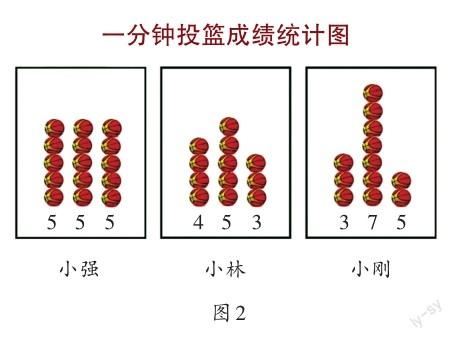

三、平均数的应用

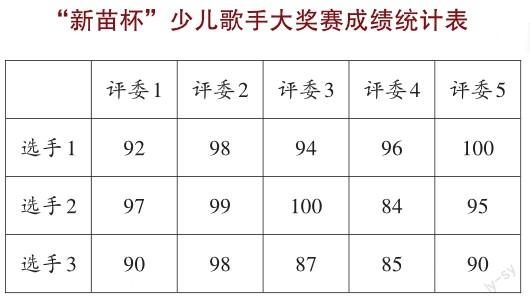
解决平均数数学问题的策略，在生活中的应用十分广泛。比如：图2中小强、小林和小刚三个人谁的投篮水平比较高？右表中选手1、选手2和选手3谁的成绩比较好？我们都要先求出平均数，才能确定谁的水平高、谁的成绩好。