基于预充电模型的直流支撑电容器状态辨识方法研究

田睿, 刘维可, 伍珣

(1. 国网湖南省电力有限公司超高压变电公司, 湖南 长沙 410004；2. 国网湖南省电力有限公司电力科学研究院, 湖南 长沙 410208；3. 中南大学交通运输工程学院, 湖南 长沙 410075)

0 引言

直流支撑电容器是功率变流器的关键器件之一, 能平衡变流器输入与输出之间的瞬时功率差,大幅减小直流环节的电压变化, 为后级负载提供稳定的直流支撑电压, 广泛应用于机车牵引、 航空航天、 风力发电、 光伏发电等领域。

然而, 受环境温度、 谐波、 过电压等影响, 直流支撑电容器在使用一段时间后性能退化, 失效率上升, 极易损坏[1－4]。 统计结果显示, 在功率变流器故障中, 由电容器故障导致的情况占比高达30%[5]。 直流支撑电容器老化失效的重要特征是电容量持续下降, 当电容量下降超过5%[6－8]时, 认为其寿命达到服役终点。 因此, 有必要对直流支撑电容器状态进行定期监测以保障工作安全、 稳定。

近年来, 国内外涌现大量有关电容器状态辨识的研究成果。 注入电流法是一种常见的电容器状态监测技术。 LEE D C 等人[9]向交直交型脉宽调制(pulse width modulation, PWM) 变换器的输入端注入低频交流电, 观测输出端直流电压电流中的纹波分量, 以此估计支撑电容的电容量。 文献[10]将可控的交流电流注入三相交直流PWM 变换器的输入端, 借助数字滤波器改变输出端的交流分量并计算电容器的等效串联电阻。 LEE K W 等人[11]对逆变器铝电解电容进行监测, 在电机停转时对定子绕组施加恒定占空比的电压, 据此估算的电容值和等效串联电阻值最大误差在5% 以内。 ABOKHALL A G 等人[12]提出将可控的交流电压注入直流侧, 并使用支持向量回归方法计算电容值, 该方法最大检测误差仅为0.15%。 尽管注入法可以获得较为理想的辨识精度, 但极易引入额外谐波, 给系统稳定性带来一定影响。

不借助外部注入信号, 通过电路模型也可以对电容器状态进行辨识。 姚凯等人[13－15]提出一种基于采样周期中特定时刻的纹波量辨识电容值的方法, 在Boost PFC 变换器中实验效果良好, 电容量的辨识误差在3.5%以内。 ARYA 等人[16]根据2 次谐波阻抗辨识光伏逆变器电容器电容量值, 但在逆变器样机中的试验效果不佳, 最大误差为14.7%。AHMAD 等人[17]使用与变换器开关频率相同的采样频率测量电容电流以消除开关频率的谐波分量,在此基础上利用二次谐波阻抗估计电容量值, 最大辨识误差为2.56%。

目前, 直流支撑电容器状态辨识还存在如下问题有待解决: 在直流电压较高场合, 用于测量电容器电压的传感器具有较大绝对误差, 测量噪声幅值与直流电压纹波分量接近, 导致现有方法出现较大辨识误差。 针对上述问题, 提出一种基于预充电过程的电容量辨识方法, 该方法通过构建预充电模型, 采用递推辅助变量最小二乘法对模型参数进行估计, 从而得到准确的电容器电容量辨识结果。 与现有技术相比, 本文提出的方法可以有效减小测量噪声对辨识结果的影响, 具有较好的鲁棒性。

1 直流支撑电容器与预充电模型

1.1 直流支撑电容器

目前, 广泛使用的直流支撑电容器有铝电解电容器和金属薄膜电容器[18－20], 性能对比如图1 所示。 在许多工业系统中, 铝电解电容器因为拥有高电容密度和低成本的优势, 成为直流链路电容的常用选择。 但铝电解电容器仍有许多不可忽视的缺点, 如对温度变化敏感、 滤波带宽有限等。 以薄膜技术为支撑的金属薄膜电容器越来越多地取代铝电解电容器发挥作用, 具有较低的等效串联电阻、 良好的滤波带宽和独特的自愈特性。 此外, 金属薄膜电容器是金属基结构, 对温度、 湿度等环境变化不太敏感。 因此, 采用薄膜电容器作为直流支撑电容器是当前的主要趋势。

图1 铝电解电容器、 金属薄膜电容器性能对比

薄膜电容器由阴阳极金属箔、 中间绝缘电容薄膜、 金属壳或其他具有绝缘性质的外壳组成[21]。在制作上, 将金属电极轧成箔后和绝缘电容薄膜卷绕构成电容内芯, 这样能够尽可能减小电容体积以增加电容量密度。 受制作工艺、 工作频率和环境条件的影响, 实际电容器可能伴有寄生电感、 等效串并联电阻。 因此, 电容器可以等效为电容与电阻的串联形式, 如图2 所示。

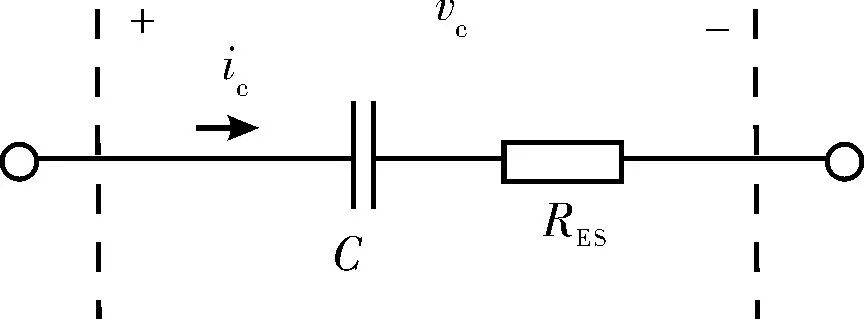
图2 电容器等效电路

1.2 预充电过程及模型

图3 为一种常用的变流系统拓扑, 包含整流器、 中间直流环节及三相逆变器。 其中,C为直流支撑电容器,R1为预充电电阻。 预充电过程在变流器运行前开始, 接触器K1断开,R1接入电路；接触器K2断开, 三相逆变器、 放电电阻与直流环节断开。 整流器输出的直流电压经充电电阻R1为直流支撑电容器充电, 此时电压传感器监测直流电压u1与电容电压u2。 当两者电压差小于一定值时,预充电过程结束, 逆变器投入运行。

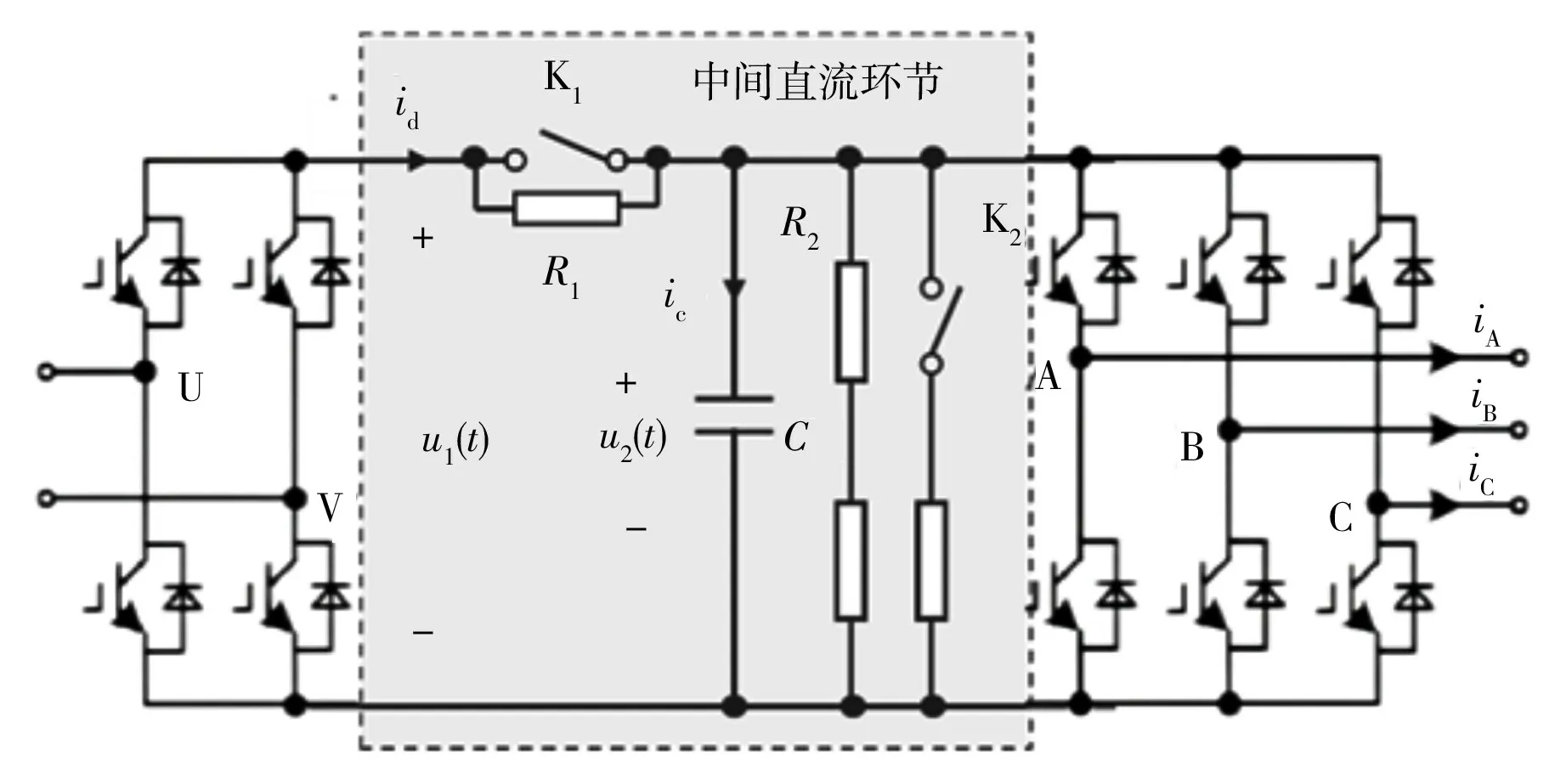
图3 变流系统拓扑

可知, 预充电过程简化后的等效电路模型如图4 所示。

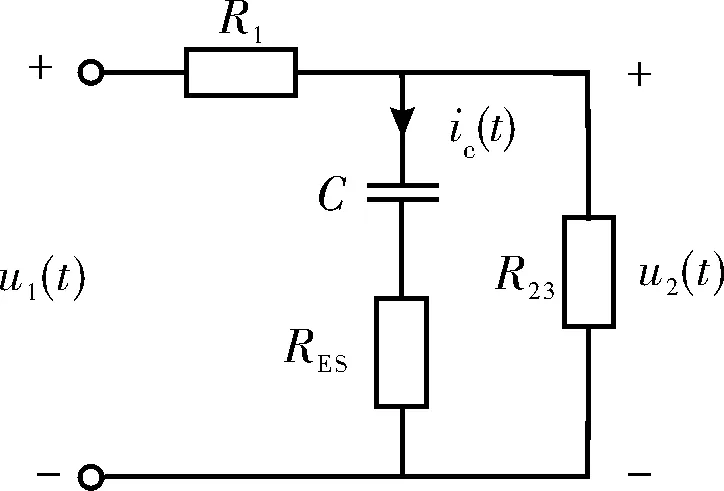
图4 预充电过程简化电路

根据基尔霍夫定律, 计算流经支撑电容的电流ic:

电容电压可表示为:

在复频域中, 上式可描述为:

采用双线性变换将其离散化, 整理后得:

式中

可得到电容量C的计算公式:

因此, 通过辨识b0和b1即可得到电容量的值。

2 基于递推辅助变量最小二乘法的电容器状态辨识

传统的递推最小二乘法只适用于白噪声系统,当系统先测数据存在有色噪声时, 传统的递推最小二乘法在迭代次数逐渐增加时是有偏差的； 引入辅助变量可以校正偏差, 有效提高辨识准确度。 因此, 在预充电过程中, 采用递推辅助变量最小二乘法辨识直流支撑电容健康状态, 能够在更广泛的工程实际情况下保证较好的估计准度。

将系统差分方程写为最小二乘格式, 为:

式中

式中,u2(k) 为系统的输出；θ是待辨识的系统参数；φ(k) 是可观测数据向量。 以表示θ的估计值,表示u2的估值, 则有系统估计:

系统残差δ(k) 可表示为:

以残差平方和为辨识准则, 准则函数表达式如下所示:

最小二乘原理要求残差的平方和为最小, 因此, 令J(θ) 最小的系统参数估值即为最小二乘估值。 当J(θ) 导数值为0 时, 即可得到最优估计值。

递推最小二乘算法是在一次性算法的基础上,按观测次序引入新的观测数据逐步修正估计, 经过多次迭代求得最终估计结果。 以表示θ在k时刻的估计值, 递推公式为:

式中,K(k) 为增益矩阵；P(k) 为协方差矩阵, 初值可设为P＝m2I,m为足够大的实数。

在有色噪声情况下, 递推最小二乘法的辨识结果是有偏的, 因此引入辅助变量法。 利用Tally 原理构造辅助变量矩阵Z来修正误差项δ, 有:

整理得辅助变量法下系统参数的最小二乘估计值:

求期望, 可得:

引入辅助变量Z矩阵后, 迭代公式改进如下:

采用辅助变量法进行系统辨识时, 可以先用递推最小二乘法迭代一定次数, 获得估计结果, 再将其作为辅助变量法的启动初值进行无偏估计。 至此, 通过上述算法可以求得准确的电容量估计值。

3 方法验证

选取一个6.81 mF 的薄膜电容器为测试对象。考虑到工程应用中存在较大测量噪声, 在方法验证中对试验环境下的电压信号人为添加一定方差的噪声, 用于模拟实际噪声情况。 为了探究方法的性能, 电压信号的采样频率分别设置为200 Hz、500 Hz、 700 Hz、 1 kHz。 设定算法在前50 次迭代使用递推最小二乘法辨识, 从第51 次后开始进行递推辅助变量法辨识。

图5 和图6 分别给出了无噪声和有噪声下的电容量辨识结果。 可以看出, 采样频率在500 Hz、700 Hz、 1 kHz 时, 观测数据无噪声, 辨识精度达1%以内； 观测数据含噪声, 辨识精度达2%以内。而采样频率为200 Hz 时, 观测数据无噪声, 辨识误差小于2%； 观测数据含噪声, 前期迭代结果产生尖峰, 计算结果与真实值相差较大。 分析原因,由电容器充电过程可知, 在预充电过程前期电容电压较小, 而试验验证时设置了传感器测量噪声方差使前期数据偏差较大。 同时, 采样频率低意味着辨识数据量较少, 迭代次数随之减少, 而采样点电压噪声大, 导致辨识效果与其他采样频率下的效果相差较大。

图5 无噪声添加时的电容量辨识结果

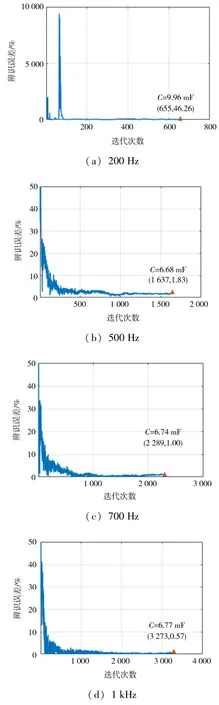
图6 噪声方差σ2 ＝3 时的电容量辨识结果

在200 Hz 采样频率下将噪声方差降低至1, 继续进行辨识测试, 结果如图7 所示。 可以发现, 迭代初期的发散情况被修正, 电容量辨识结果近似收敛。 尽管最终辨识的相对误差为9%, 但仍与更高采样频率下的辨识精度有一定差距, 说明除噪声外, 该算法效果受制于迭代次数, 在低频下受噪声影响较大。 因此, 在使用递推辅助变量法进行电容器状态辨识时, 要综合考虑噪声大小与采样频率的平衡关系, 避免辨识失效。

图7 噪声方差σ2 ＝1、 采样频率f＝200 Hz 时的电容量辨识结果与误差

为进一步确定递推辅助变量法参数辨识的收敛性, 表1 给出了噪声方差σ2＝3, 采用500 Hz、700 Hz和1 kHz 的采样频率时, 辨识误差收敛于5%、 2%、 1%所需要的迭代次数及最终辨识结果。

表1 噪声方差σ2 ＝3 时的电容量辨识收敛情况

从表中可以看出: 1) 在三种采样频率下, 辨识误差均可收敛至2%以内, 说明该方法能较为准确地辨识电容器电容量, 满足及时监测电容器老化失效的要求； 2) 该方法估计误差收敛至5%所需要的迭代次数为260 次、 387 次和327 次, 能够较为快速地收敛； 3) 采样频率为500 Hz、 700 Hz时, 最终辨识相对误差大于1%, 采样频率为1 kHz时, 相对误差小于1%, 说明电容量辨识结果的相对误差随着采样频率的提高而降低, 即辨识精度随之提高。

4 结语

本文针对直流支撑电容器状态辨识在较大测量噪声情况下的辨识精度问题, 提出一种基于预充电过程的电容量辨识方法。 该方法通过建立预充电模型来削减测量噪声对信号测量的干扰, 通过递推辅助变量最小二乘法对模型参数进行辨识, 从而得到准确的电容量辨识结果。 验证结果表明, 该方法能够有效抵御测量噪声的不利影响, 在500 Hz 以上的信号采样频率下可以得到较好的辨识结果, 当采样频率为1 kHz 时, 电容量辨识误差为0.569%。