基于多元回归分析及迭代线性规划的多断面有功潮流控制算法

羿敏, 赵邈, 周恒逸

(国网湖南省电力有限公司电力科学研究院, 湖南 长沙 410208)

0 引言

随着我国电力需求的快速增加, 输电断面功率越限的问题日益突出, 导致电网安全裕度降低[1－2]。 如果重载线路跳闸, 会使潮流大规模转移, 甚至发生大规模停电事故。 因此, 为了提高系统的安全裕度、 提高区域传输极限和优化系统的运行方式, 需要对断面潮流进行精确的控制[3－5]。

目前对断面潮流进行控制的方法主要包括优化控制[6－10]和灵敏度分析[11－13]。 文献[6] 基于连续线性规划技术提出了基于灵敏度的线性规划方法,但是该算法需要调整的设备数目太多且计算量较大； 文献[9] 提出了一种基于线性规划算法的安全约束调度方法, 该方法同时考虑了安全约束和经济性, 但是不能保证调整后所有线路都不越限。 文献[10] 基于发电机的转移分布因子, 提出单个输电断面的有功安全校正算法, 但该算法只对单断面进行控制, 没有考虑对其他断面的影响； 文献[4] 基于直流潮流模型提出了直流潮流灵敏度的断面功率控制算法, 该方法能够对断面总潮流和支路潮流进行精确控制, 但是忽略无功的影响易产生较大的误差。 统一潮流控制器能够对断面潮流进行有效的控制, 但是由于价格昂贵, 目前情况下不可能大范围推广使用。

多断面协同控制算法目前常采用的算法有预分配功率法[11]、 最优潮流法[12]、 扩展潮流法[13]等。文献[11] 提出的预分配潮流法具有原理清晰、程序兼容性高等优点, 但是收敛性较其他方法差。优化方法是在系统指定参数、 断面交互功率设置值下, 通过运筹学的优化方法进行求解。 该类优化方法算法成熟, 但是计算量大。 另一类扩展潮流法将断面功率约束扩展入潮流方程, 具有较好的收敛性, 但对底层潮流算法改动大。 因此, 有必要研究有效且计算复杂度低的多断面协调控制方法。

考虑多断面的协调控制, 本文提出一种基于多元回归及迭代线性规划的多断面有功潮流控制算法。 该算法选取区内发电量和负荷作为自变量对断面潮流进行多元回归分析； 考虑系统各类约束条件, 建立迭代线性规划求解模型； 最后利用该模型对目标调整量进行各机组出力调整量的计算。 利用IEEE 39 节点系统进行仿真试验, 结果表明, 该方法能够对多个断面有功潮流进行精确的控制, 不受区域内部网络拓扑变化影响, 且计算速度快。

1 断面有功潮流多元线性回归

1.1 自变量选取

电力系统中的元件众多, 特征量庞大。 从庞大特征量中筛选出对断面有功潮流控制最有效的特征量是解决问题的关键。 这些有效的特征量用于断面有功功率的控制, 因此也称为自变量。

进行多元回归的自变量需要遵循如下原则:

1) 选取的自变量能够控制。 多元线性回归一般用于对某个变量进行预测, 如负荷预测。 而本文的目的不是对断面有功潮流大小进行预测, 而是找到断面有功潮流大小的控制方法。

2) 自变量的个数应较少。 实践表明, 断面有功潮流与发电机出力及负荷具有较强关联性。 大型互联电网中发电机和负荷数目庞大, 如果将所有发电机和负荷作为拟合断面有功潮流的自变量, 会导致回归模型复杂、 模型过拟合造成的精度降低、 估计方差扩大等问题[14]。 因此, 自变量的选取个数应该尽可能少。

3) 回归效果好。 在自变量个数较少的情况下还应使回归效果尽可能好, 回归效果取决于自变量的好坏, 回归效果也将直接影响断面有功潮流控制的精度。

根据上述原则并综合考虑如下因素: ①断面潮流的控制方式主要有调整发电机出力、 切负荷、 调制直流支路传输功率等[15]； ②电力系统的分区及电力系统分区调度的特点[16], 选取区内机组出力和区内负荷大小作为自变量。

1.1.1 集合定义

假设系统有m个断面将系统分成了n个区域。用S表示断面集合,A表示区域集合。

断面有功潮流数据集合如式(1) 所示。

区域发电量数据集合、 负荷大小集合、 自变量集合表示如式(2) 所示。

式中,PAi、LAi、xi这三个变量都是与ySi一样的向量。

1.1.2 自变量的筛选

对任意断面来说, 与相邻区域发电量和负荷相关程度较大, 与电气距离较远区域的发电量和负荷相关程度很小。 因此, 对任意断面进行回归分析需要从自变量集合X中选取相关程度较高的自变量。具体筛选步骤如下。

步骤1, 计算相关系数。 为了表征断面潮流和自变量之间的相关程度, 采用皮尔逊(Pearson)相关系数。 Pearson 相关系数可以定量描述两变量x与y间的线性相关程度, 计算公式为:

式中,rxy为自变量x与y的相关系数且rxy∈[－1,1] 。 相关系数绝对值越大, 则相关程度越高, 相关系数绝对值越小, 则相关程度越弱； 相关系数大于0, 则两个变量为正相关, 反之为负相关。 计算所有断面和自变量的Pearson 相关系数得到相关系数矩阵如下:

式中,ri,j表示为第i个断面和第j个自变量的Pearson 相关系数, 其中i＝1, 2, …,m；j＝1,2, …, 2n。

步骤2, 形成逻辑相关矩阵。 为了尽可能精确, 如果ri,j小于0.2, 则认为第i个断面和第j个自变量不具有相关性, 置φi,j＝0； 否者置φi,j＝1。可以得到逻辑相关矩阵如式(5) 所示, 该矩阵用于回归模型。

1.2 多元线性回归模型

断面潮流的多元线性回归数学模型, 用于描述断面潮流和自变量之间的关系。 考虑逻辑相关矩阵, 第i个断面的多元线性回归模型表示为:

式中,βi,0为常数项；βi,j为回归系数, 当φi,j＝0时,βi,j＝0；εi为不可观测的随机变量。 根据样本数据可以计算出回归模型中的参数。

2 多断面有功潮流调整模型

2.1 公式推导

当系统状态发生改变时, 式 (6) 变为式(7):

式中,ΔySi为断面Si有功潮流改变量；Δxj为第j个自变量的改变量。 式(7) 减去式 (6) 得到式(8):

2.2 多断面优化调整模型

回归模型能够对断面有功潮流预测。 但式(6) 所示的多元回归方程是不定方程, 数学上存在无穷多的解, 因此回归模型不能用于控制。 本文在回归模型的基础上, 通过构建多断面优化调整模型, 实现断面功率的有效控制。 多断面优化调整模型以断面调整误差最小为目标函数, 同时考虑机组的出力约束, 模型描述如下。

1) 变量选取。 多断面有功潮流调整模型选取区域发电量、 负荷量, 发电机有功出力、 无功出力为控制变量； 选取各个断面有功潮流作为状态变量。

2) 目标函数

式中,f为调整误差, 即关注断面拟合调整量与目标调整量差值的绝对值的和；ΩZ为关注断面的集合；ΔySi,d为断面Si的目标调整量。

3) 等式约束。 不考虑网络损耗变化的情况下, 多断面调整模型的等式约束条件为系统功率平衡约束。

4) 不等式约束。 多断面调整模型的不等式约束包括各区域机组出力调整上下限, 区域负荷调整上下限, 和不关注断面调整量的上下限。

式中,pmax,j、pmin,j分别为发电机j有功出力上、 下限；p0,j为发电机j调整前的有功出力值；Ωg,Ai为区域Ai的发电机集合；Lmax,j、Lmin,j分别为负荷j有功需求上下限；L0,j为负荷j调整前的有功出力需求值；ΩL,Ai为区域Ai的负荷集合。 假设尽量不损失负荷, 则负荷调整量Δxi(i＝n＋1, …, 2n) 等于0。

目标函数(9) 和约束条件(10)、 (11) 一起构成了多断面有功潮流调整模型。

5) 发电机出力调整。 根据多断面调整模型计算出各区域发电调整量, 在此基础上还需要计算出每台发电机出力的调整量。 按照机组备用容量大小进行出力分配, 对区域i内的各机组出力按式(12) 进行调整。

式中,pj、qj分别为区域i内第j台发电机调整后的有功、 无功出力值；p0,j、q0,j分别为第j台发电机调整前的有功、 无功出力值；pm,j、qm,j分别为第j台发电机的有功、 无功出力限值, 当Δxi ＜0 时, 取机组最大有功、 无功输出功率, 反之取机组最小有功、 无功输出功率。

2.3 迭代多断面调整算法

求解优化模型, 可以得到发电机出力的调整量。 潮流方程本质是高阶非线性方程组, 本身的非线性特征导致一次调整后潮流断面功率并不能达到设定值。 因此, 提出迭代多断面调整算法。

迭代多断面调整算法的步骤为: 1) 首先根据调整后机组出力值, 重新进行潮流计算； 2) 根据潮流计算结果, 得到调整后的断面潮流值； 3) 计算调整后断面潮流值与调整前断面潮流值的差, 此差值称为实际调整量； 4) 计算实际调整量和目标调整量之间的差值； 5) 若差值小于某给定限值,则结束迭代； 否则返回第1) 步。

在以上步骤中, 实际调整量和目标调整量之间的差值作为下次迭代的目标调整量。 通过上面的步骤, 直到实际调整量和目标调整量之间的差值小于某一限值, 结束迭代。

3 算法流程

算法的详细计算流程如图1 所示。

图1 迭代多断面有功潮流调整算法流程

步骤1: 输入数据。 输入数据包括多元回归分析中得到的回归系数矩阵, 算例系统的原始数据:母线数据、 发电机数据、 线路数据等。

步骤2: 给定各断面需要的调整量。

步骤3: 置迭代次数K＝0。

步骤4: 根据最优调整模型计算各区域机组出力的调整量。 最优调整模型的目标函数不变； 约束条件中的各区域调整出力上下限会随着迭代次数不同而改变。 第一次迭代出力调整最大限制为区域最大出力减去基态潮流下区域的出力； 第二次迭代时, 调整出力的最大限制为区域最大出力减去第一次调整后区域出力, 依此类推。

步骤5: 置迭代次数K＝K＋1。

步骤6: 累加前K次区域机组出力的调整量。

步骤7: 机组出力调整。 根据区域出力的调整量和机组的备用容量确定区域内每台机组的调整量。

步骤8: 计算潮流。 根据更新后的算例系统数据, 计算潮流、 各断面有功潮流大小、 实际调整量, 以及实际调整量和计划调整量的差值。

步骤9: 判断是否结束迭代。 判断误差是否小于设定的限值, 或者是否大于最大迭代次数Kmax,两者只要满足一个则结束循环。 否则, 计算新的调整量, 返回步骤4 继续迭代。

步骤10: 判断K是否小于等于Kmax。 如果K小于等于Kmax, 则输出找到可行解和各机组出力改变量； 否则, 输出没有找到可行解, 并输出误差大小和各区域有功出力调整量。

4 算例分析

4.1 IEEE 39 节点系统验证

以图2 所示的IEEE 39 节点系统为例, 验证本文方法的有效性。 根据谱聚类算法[16－17]将系统划分为三个区域, 三个区域之间一共有三个断面, 断面之间的联络线见表1。

表1 IEEE 39 节点系统断面及其包含线路

图2 IEEE 39 节点系统分区示意图

4.1.1 样本生成

系统负荷水平、 发电机组出力分别在73%～100%的基准负荷水平、 基准发电机出力水平下,以3%的步长变化, 得到10 组样本； 对每一组样本的所有负荷和发电机, 出力大小在8%左右随机波动, 生成100 种样本, 合计得到1 000 个运行样本。

4.1.2 相关系数计算

根据生成的样本数据, 计算断面有功潮流与自变量之间的偏相关系数, 见表2。 需要说明的是,生成样本个数、 生成方法会对相关系数计算产生影响, 经试验证明, 此影响较小。

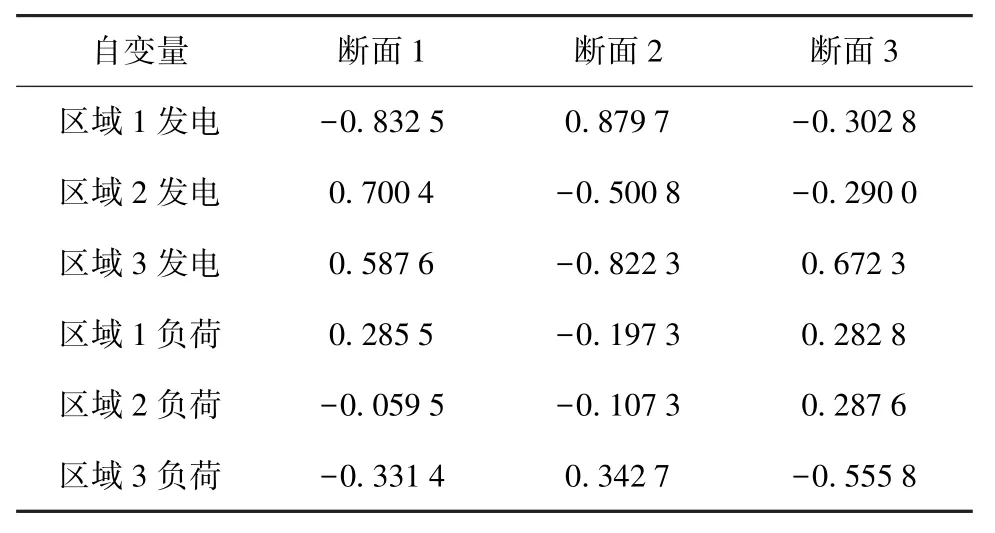
表2 断面潮流和自变量的偏相关系数

4.1.3 多元回归

根据多元回归模型, 进行三个潮流断面的多元回归分析。 各个回归系数及回归效果都进行了显著性检验, 形成的回归系数矩阵如下。

4.1.4 多断面调整

对本算例系统, 由于断面1、 3 潮流较大, 断面2 潮流较小, 选取断面1、 3 为关注断面, 断面2 为不关注断面。 为了证明本算法的有效性, 设置不同的场景。

1) 情景1: 断面1 潮流降低40 MW, 断面2为不关注断面, 断面调整上、 下限分别为30 MW、－30 MW, 断面3 潮流降低20 MW。 计算可得各断面调整误差随迭代次数的变化, 及发电机出力改变量, 分别如表3 和图3 所示。

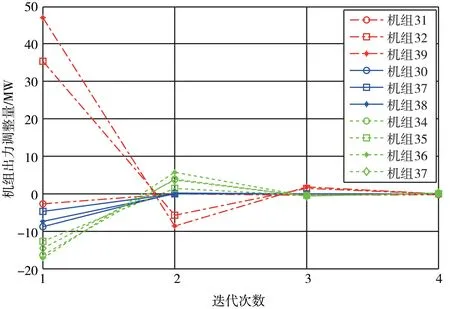
图3 情景1 下机组出力调整量随迭代次数变化

2) 情景2: 断面1 潮流降低40 MW, 断面2潮流调整量绝对值上限为25 MW, 断面3 潮流降低25 MW。 计算可得各断面调整误差随迭代次数的变化及发电机出力改变量, 分别如表4 和图4 所示。

表4 情景2 下断面潮流控制效果MW

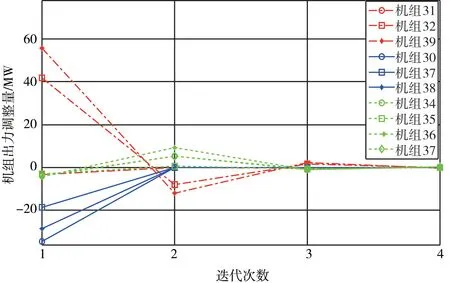
图4 情景2 下机组出力调整量随迭代次数变化

可以看出, 随着迭代次数的增加, 断面潮流大小越来越接近控制目标, 机组出力的变化量越来越小； 表4 的控制误差比表3 大, 这是因为情景2 下断面2 的调节量绝对值大小从30 MW 减小到了25 MW。

5 结语

本文结合大电网分区调度的实际情况, 研究区内发电量、 负荷与断面有功潮流大小的关系, 并结合线性优化方法, 提出多断面有功潮流控制方法,该方法能够对多个断面有功潮流进行精确的控制。相较于灵敏度算法, 本文的方法能够实现多断面潮流协同控制。 相较于其他最优化方法, 本文方法不存在收敛性问题且计算量小。

由于本文只对断面上总有功潮流进行了控制,并没有对断面内的单条线路上的潮流进行控制, 如何在协调控制多断面有功潮流的情况下对单条线路进行控制, 将是今后研究的重点。