深海载人平台舵翼结构疲劳可靠性分析
杜一凡,郝 恒
(1.中国船舶科学研究中心深海载人装备国家重点实验室,江苏无锡 214082;2.深海技术科学太湖实验室,江苏无锡 214082)
0 引言
深海载人平台是人类进行深海探测、开采深海资源的重要装备,其舵翼结构是保证平台操纵性和稳定性的重要装置。舵翼结构在水面航行时承受巨大的波浪砰击载荷和海水动压力,若长期服役,其很可能发生疲劳破坏,导致安全事故发生。因此,有必要保证深海平台舵翼结构在寿命期的疲劳可靠性。
深海载人平台舵翼结构设计主要参考潜艇相关规范,但规范[1-2]中关于舵翼结构的设计,没有考虑结构疲劳,也没有考虑可靠性相关问题,不能直接作为判断结构长期服役疲劳可靠性水平的依据。文献[3]对船舶舵装置单次工况下的可靠性进行研究,提出舵装置可靠性设计方法,分析了不确定因素对舵装置可靠性的影响;文献[4]对深海平台操舵机构进行了运动精度可靠性分析,并研究了运动精度与舵叶偏角之间的关系。以上关于舵翼结构设计的文献均未提及疲劳可靠性问题。中国船级社相关规范给出了船体结构通用的疲劳强度评估方法和建议的S-N 曲线[5],其评估方法可以为深海载人平台舵翼结构疲劳可靠性评估提供参考。
本文对深海载人平台舵翼结构疲劳可靠性进行研究,分析了舵翼结构各部分的主要疲劳载荷和结构热点。以升降舵结构为例,建立了深海载人平台舵结构疲劳可靠性分析模型,并对相关疲劳可靠性设计问题进行探讨。
1 舵翼结构疲劳可靠性问题
1.1 工况与热点
深海载人平台舵翼结构包括稳定翼、方向舵与升降舵。稳定翼结构的疲劳载荷主要为水面波浪砰击,结构热点出现在翼梁根部与艇体框架焊接处;方向舵结构的疲劳载荷主要为水面海水动压力与水下偏舵状态下的水动力载荷;升降舵结构的疲劳载荷主要为水面波浪砰击与水下偏舵状态下的水动力载荷。方向舵与升降舵结构热点出现在舵轴与舵叶根部连接处、舵锺梁根部与艇体框架连接处。以下舵翼结构疲劳可靠性评估以舵轴与舵叶根部连接处的舵叶结构为例。
1.2 可靠性定量要求
目前,深海装备领域暂无安全性与可靠性定量指标的相关规范,一般参考GB 50153—2008《工程结构可靠性设计统一标准》和GB 50158—2010《港口工程结构可靠性设计统一标准》中相关结构可靠性的定量要求。港口工程结构的可靠性指标要求[6]用可靠性系数表示,如表1所示。
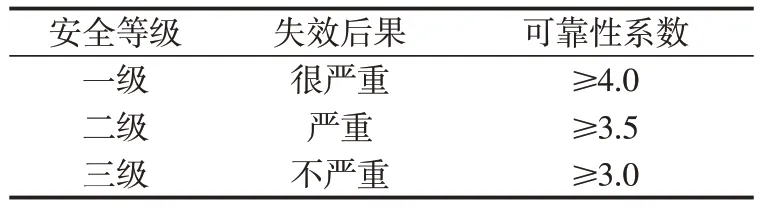
表1 港口工程结构的可靠性指标Tab.1 Reliability index of port engineering structure
深海载人平台舵翼结构损坏后可能导致平台撞上船只或大型海洋生物,造成平台结构严重损坏。同时,舵翼结构损坏后须要返回基地维修,导致出航任务终止,因而舵翼结构破坏属于二级事故。结构疲劳可靠性随服役时间降低,但仍须要其能满足定量可靠性要求,即深海载人平台舵翼结构服役末期的疲劳可靠性系数不小于3.5。
2 舵结构疲劳可靠性分析方法
2.1 基于不确定因素的疲劳寿命公式
本文采用Miner线性累积损伤模型结合S-N曲线进行深海平台舵翼结构疲劳可靠性分析。
在船舶与海洋工程中,通常采用如下形式的S-N曲线:
式(1)中:N为应力循环次数;S为应力范围;A和m为材料属性。
结构疲劳可靠性计算中,采用的是中值S-N 曲线[7],即存活率为50%。
基于Miner 线性疲劳累积损伤理论,结构节点在时间L内的总累积损伤度为:
式(2)中,Di为结构节点在应力范围为Si下的累积损伤度。
深海平台升降舵结构的主要疲劳工况为水面状态的波浪砰击工况和水下航行变深状态的水动力工况[8]。升降舵结构的总疲劳损伤为以上2 种工况导致的疲劳损伤之和,即:
式(3)中:DT为总的疲劳累积损伤;D1、D2分别为波浪砰击工况和水动力工况导致的疲劳累积损伤。
下面分别计算2种工况导致的疲劳累积损伤。
1)波浪砰击导致的疲劳累积损伤。
升降舵结构在时间T内的疲劳累积损伤D1为[6]:
Ω1为波浪砰击工况下定义的应力参数:
式(5)中:fL1为波浪砰击应力范围发生的平均频率;S1为波浪砰击工况的应力范围;fS1(S1) 为波浪砰击载荷的概率密度函数。
船舶及海洋工程结构疲劳可靠性分析中,常用韦布尔分布描述波浪载荷导致的应力长期分布[9],概率密度函数为:
式(6)中:α为尺度参数;ξ为形状参数。
尺度参数α按“一生中一遇”定义,即在载荷谱回复周期L1期间,大于SL1的应力范围仅可能出现1次。尺度参数α[10-11]为:

根据Miner线性累积损伤理论,当DT=1 时,结构会发生疲劳破坏,由此可得升降舵结构的疲劳寿命:
式(14)中:参数A是1个随机变量,反映了材料疲劳强度的不确定性。同时,应力参数Ω也反映出疲劳载荷的随机性,所以结构的疲劳寿命也是随机的。
此外,在结构寿命的计算中还有2 个重要的不确定因素需要考虑。首先,在计算疲劳载荷的过程中,对海况的描述、波浪荷载的计算、有限元结构应力分析等方面都采用了很多假设或理想化的计算模型,得到的应力范围与结构在真实环境中产生的应力范围之间必然存在误差。这种误差是随机的、不确定的,可用随机变量表示为:
式(15)中:Sa为结构在实际环境中产生的应力范围;S为计算得到的应力范围;B为用于反映疲劳载荷计算过程中的不确定性的随机变量。因此,实际环境下的应力参数为:
此外,Miner 线性累积损伤理论本身具有不确定性,结构在真实情况下破坏时的累积损伤度并不总是等于1。在分析时,可采用随机变量Δ 来表示真实结构发生疲劳破坏时的累积损伤度,即当构件发生疲劳破坏时,DT=Δ。
综上可得深海平台升降舵结构的疲劳寿命为:
2.2 参数不确定性分析
1)S-N 曲线的斜率m。
根据以往对实际构件的疲劳试验数据进行分析,证明m的分散性很小,即m可看作为确定值[10]。
2)S-N 曲线参数A。
在给定的应力循环范围S下,lgN服从正态分布,当m是1个确定值,那么lgA也可以看作为1个服从正态分布的随机变量。
参数A的变异系数可以通过试验数据进行拟合,缺少试验数据时,可以参考英国标准协会(BSI)和英国能源部(UK DEn)推荐的数据,推荐的8条S-N曲线的参数A变异系数范围在0.431~0.629,均值为0.51。
3)疲劳累积损伤极限Δ。
Wirsching等经过大量试验和研究后,认为在船舶及海洋工程结构中Δ 服从对数正态分布,并取Δ 的中值和变异系数分别为1.0和0.3[12]。
4)应力参数B和Ω。
在进行疲劳可靠性分析时,将Ω视作确定值,而疲劳应力的计算过程中,所有的不确定因素都由B来描述[13],随机变量B如下计算:
式(18)中:M为结构加工工艺;S为海浪描述;F为波浪力计算;N为名义应力计算;H为应力集中系数。
Bi服从对数正态分布,B的中值和变异系数分别为:
式(19)(20)中,B͂i和CBi分别为各Bi的中值和变异系数。
表2列出了世界上一些海洋工程和石油公司统计归纳出的各Bi的统计特征参数[10,14],可供参考。对海洋结构和普通船舶结构计算时,B的中值和变异系数分别取0.7和0.5[15-16]。
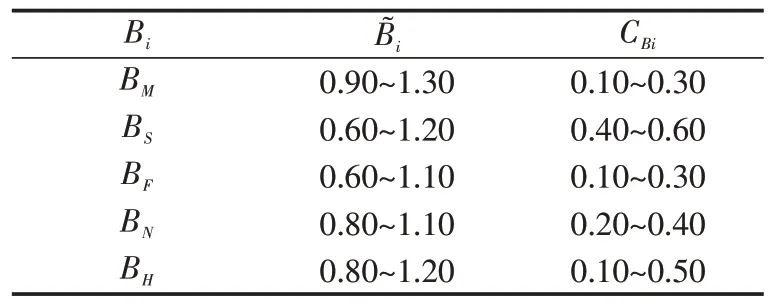
表2 Bi 的经验资料Tab.2 Empirical data of Bi
2.3 疲劳可靠性模型及可靠度计算
舵结构设计时一般会给出设计寿命TD。当计算得到的疲劳寿命Tf大于或等于设计寿命TD时,就认为结构是安全的;反之,则认为结构不安全。由此可得安全裕量为:
可靠性系数为:
2.4 低应力范围作用下疲劳损伤的修正
上文采用单直线形式的S-N曲线计算疲劳累积损伤,但很多材料,特别是船用钢,在低应力范围作用的高寿命区,S与N之间的关系与中等寿命区是不同的。为反映这一性质,S-N 曲线常采用双直线形式[17],即应力范围小于SQ。S-N 曲线的参数为m′和A′,应力范围大于SQ,S-N 曲线的参数为m和A,SQ为2条直线相交点对应的应力范围值。双直线形式的S-N 曲线如图1所示。

图1 双直线形式的S-N曲线Fig.1 S-N curve in double straight line form
考虑低应力范围作用下疲劳损伤修正后的应力参数定义为:
式(23)中,Λ为修正系数。
波浪砰击载荷属于连续性载荷谱,修正系数为[10,18]:

修正后的深海平台升降舵结构的疲劳寿命为:
3 舵结构疲劳可靠性设计
3.1 确定寿命下的疲劳可靠性计算
工况:深海载人平台设计寿命为20 a,每年执行任务和训练时间约为200 d。其中,水面航行的时间约60 d,水面使用最大海况5级,水下变深时升降舵舵角为15°或30°,单潜次作业平均约变深50 次,平均每年下潜作业15次,15°和30°舵角的使用频率为1 ∶1。
深海平台舵装置结构材料为Q345 号钢,对于焊接节点,适用于英国能源部推荐的8 条S-N 曲线中的D 曲 线[5]。有 关 数 据 为:m=3.0 ,A͂=3.988×1012,m′=5.0 ,A͂′ =1.138 × 1016,CA=CA′=0.512 ,SQ=53.37 MPa。
1)波浪砰击工况下的应力参数计算。
终年在海上工作的固定式海洋平台,20 a 的波浪载荷循环次数NL=108。对于深海平台,每年水面航行时间约60 d,20 a的NL1=60 365×108=1.64×107。
波 浪 砰 击 载 荷 发 生 的 平 均 频 率fL1=NL1L1=1.64×107( )20×365×24×3 600 =0.026/s。
形状参数ξ根据航区环境、结构类型、动力性能,以及所考虑构件在整个结构中的位置等因素来确定。对在全球范围航行的船舶,可取ξ=0.91[6]。
B的中值和变异系数分别取0.7和0.5。
深海平台舵翼结构与常规潜艇舵结构载荷工况类似,最大工况为水面波浪砰击且远大于水下工况,潜艇舵结构在水面工况下安全系数取1.5[1],因而深海平台舵翼结构强度安全系数取值为1.5。按照此要求设计的深海平台舵装置最大应力范围SL1=σs/1.5=345/1.5=230 MPa。
将以上数据代入式(10),得到波浪砰击工况下的应力参数Ω1为:
修正系数Λ1为:
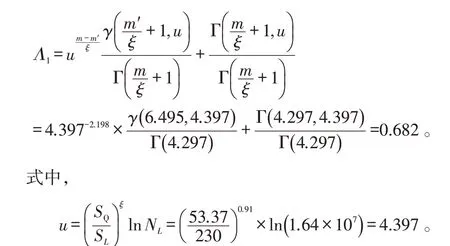
修正后的应力参数Ω1=Λ1Ω1=180.15。
2)水动力载荷下的应力参数计算。
水下变深时升降舵水动力应力范围的平均频率:
fL2=NL2/L2=50×15/(365×24×3 600)=2.38×10-5。
舵角偏转30°时,应力范围为35 MPa;舵角偏转15°时,应力范围为1 MPa。
将以上数据代入式(12)和(25),得到水动力工况的应力参数Ω2为:
修正系数Λ2为:

由结果可以看出,在以上使用工况下,根据强度安全系数为1.5所设计的舵翼结构不满足长期服役的疲劳可靠性要求,须要进行定期检修或更改设计。
3.2 满足疲劳可靠性要求的寿命计算
由式(22)变换可得疲劳寿命:
按照强度安全系数取1.5,可靠性系数满足安全等级二级要求,取3.5,计算疲劳寿命。
即满足安全等级二级要求的疲劳寿命最大为9.79 a,因而最迟需要在第9年进行舵结构疲劳损伤探测、修复或更换。
3.3 满足疲劳可靠性要求的安全系数与寿命的关系
鉴于深海平台舵装置设计时常采用强度安全系数来保证舵装置的安全性,因此有必要推导出满足疲劳可靠性要求下的强度安全系数与寿命的关系曲线,供设计人员参考。
由于升降舵结构疲劳几乎全是由波浪砰击导致的,在计算时可以忽略水下水动力工况。
深海平台舵翼结构的疲劳可靠性系数要求β取3.5,假设设计寿命为ta,寿命t与强度安全系数n的关系可由“t—u—SL—n”的顺序推导。
t—u的关系,
由式(23)推导出:
由式(27)推导出:
(28)(29)两式联立,得:

式(32)中,n为安全系数,结构材料为Q345 号钢,σs=345 MPa。
联合式(30)~(32),绘制寿命t与强度安全系数n的关系曲线,如图2所示。

图2 寿命t 与强度安全系数n 的关系曲线Fig.2 Relationship curve between life t and strength safety factor n
从图2可以看出:当设计寿命为20 a时,强度安全系数取1.8;设计寿命若为30 a,强度安全系数则取到2.0。
英国能源部推荐的S-N曲线通常适用于屈服强度小于400 MPa的钢材,没有区分钢材种类,因而对于不同的钢材安全系数取值不同,不方便指导疲劳设计。为便于指导疲劳设计,可直接将最大应力范围SL作为舵翼结构强度设计许用参考值,即强度设计要求为:σ 由式(30)(31),绘制寿命t与最大应力范围SL的关系曲线,如图3所示。 图3 寿命t 与最大应力范围SL 的关系曲线Fig.3 Relationship curve between life t and maximum stress range SL 从图3中可以看出,当设计寿命为20 a时,最大应力范围约为190 MPa。设计人员可参考图3选取不同设计寿命时的最大允许应力范围。 本文对深海平台舵装置结构疲劳可靠性问题进行研究,分析了舵翼结构的工况与结构热点,提出了舵翼结构的疲劳可靠性要求,建立了基于S-N曲线的舵结构疲劳可靠性分析方法,并对疲劳可靠性相关设计问题进行探讨。得到以下结论: 1)深海平台舵翼结构破坏属于二级事故,参考相关工程结构可靠性标准,其服役末期的疲劳可靠性系数不小于3.5。 2)深海平台升降舵与稳定翼结构的疲劳损伤几乎全部由水面波浪砰击载荷造成,进行疲劳分析时可以仅考虑水面波浪砰击载荷作用。 3)在最大5级海况、每年水面航行时间60 d的工况下,根据现行潜艇舵装置设计规范选取的1.5 倍安全系数进行设计得到的深海平台舵翼结构不满足长期服役的可靠性指标要求;若要满足此要求,应当在服役第9年进行舵翼结构疲劳损伤探测、修复或更换,或者根据满足可靠性要求的最大应力范围-寿命曲线,确定设计时的最大许用应力。 4)本文选取的S-N 曲线是英国能源部对较大范围钢材的疲劳试验数据统计分析归纳而得到,适用于屈服强度小于400 MPa 的钢材,适用范围较大意味着对特定材料存在较大误差,若想得到更准确的结果,应开展相应材料的疲劳试验获取材料的S-N曲线。
4 结论

