网联车环境下动态信号交叉口通行能力分析

徐菡，林兆丰，高佩佩，吴亚庆

（山东建筑大学交通工程学院，山东 济南 250101）

随着车联网与自动驾驶技术不断完善，不同智能化等级、不同占比的智能车辆参与到城市交通，尤其在与人工驾驶车辆混行的条件下，交通环境会变得更加复杂。目前人工驾驶情境下的交叉口通行能力的相关研究较为完备，智能网联环境下在交叉口方面的研究更加倾向于区域内自适应控制[1-2]、车速引导[3]以及各类传感器等技术方面，关于网联车背景下通行能力的研究更倾向于路段或路网[4]，而在交叉口通行能力方面的研究相对较少。

本文首先分析了网联车背景下信号交叉口控制原理，基于此分析了受动态信号控制时交叉口通行能力的计算方法，提出了一种基于最小延误模型与交叉口实际车流量确定最大绿灯时间的方法，并给出了相应的求解算法，结合道路宽度、行人步行时间以及车流量确定最小绿灯时间，最后根据现场调查数据对仿真建模中的相关参数进行标定后进行仿真，并对动态信号交叉口的通行能力进行分析。研究结果能够为网联车背景下的道路交叉口相关交通参数设计提供理论指导，有利于加强对道路的规划、设计与管理。

1 控制原理

1.1 网联车控制原理

网联车控制原理结构图如图1 所示，分别为智能云端、路侧感知设备以及智能车载设备三个模块，智能云端在整个体系中充当了大脑的作用，主要通过对车流量和交通环境数据进行分析和处理，并结合信号控制交叉口优化控制模型及相关算法对为车辆制定相应的控制策略。智能车载设备能够实时获取流量、速度、位置、天气和道路环境等信息，同时将信息传递给路侧感知设备，路测设备再将信息进行初步处理后传递到智能云端，智能云端通过对相关信息与数据进行分析与优化，为交通信号控制参数的调整提供可靠的数据支持。

图1 控制系统结构

1.2 动态信号控制原理

在动态信号控制中，实际的绿灯延长时间等于激活本次单位绿灯时间开始到下次检测到来车之间的时间，其中单位绿灯时间会有重叠的部分。原理如图2 所示。

图2 单位绿灯延时时间工作原理

通过对图2 分析可知该相位内有效绿灯总时间为每个相位绿灯延长时间U 减去各自重叠的绿灯时间Vi的总和，相位内有效绿灯总时间可表示为：

式中：Vi为各个单位绿灯延时之间重叠的时间，s；为平均重叠时间，s；n 为有效绿灯时间内到达的车辆数，辆（veh）。

动态信号配时条件下对交叉口通行能力相关参数进行计算时，通常采用有效绿灯时间与周期时长平均值进行计算。动态交通分配中交叉口通行能力可以由下式决定：

式中：Si为车道i 的饱和流率，veh/h。

2 参数优化与估计模型

最大绿灯时间与最小绿灯时间共同决定了绿灯延长时间，最小绿灯时间的设置会影响交叉口是否满足通行需求，同时也是保障通行公平性的重要前提，最大绿灯时间设置过大或过小都会影响交叉口的服务水平。

2.1 最小绿灯时间

通常情况下，最小绿灯时间需保证停靠在停车线和检测器之间的所有车辆都可以安全驶出停车线，还要保证行人、非机动车能够安全通过。因此，在本文中利用初始时间与行人过街时间对最小绿灯时间进行确定。初始时间[5]取决于排队车辆、平均车头时距和开始的延迟时间：

式中：h 为平均车头时距，s；n 为停车线与检测器间的车辆数目；K1为开始的延迟时间，s。

当交叉口流量较少时，初始时间可能并不能保证行人安全过街，为确保行人能够通过交叉口，所以每个相位的绿灯时间必须大于行人安全过街的最短时间，行人过街时间由人行横道与行人步行速度确定：

式中：di为人行横道宽度，m；V1为第15 百分位行人步行速度，一般为1.5m/s；Ii为绿灯间隔时间，一般取5s。对于车道数较多的交叉口，可以考虑设置2 次过街。所以最小绿灯时间：

2.2 最大绿灯时间

2.2.1 模型建立

通过对交叉口延误模型的分析与比较，采用Webster 延误模型[6]在较高饱和度时的计算公式对动态信号配时的最大绿灯时间与周期时长进行优化。模型建立如下：

2.2.2 模型求解

针对提出模型的基本形式，选择Frank-Wolfe 算法[7]对模型进行求解。Frank-Wolfe 是求解线性约束问题的一种算法，其基本形式为

式中：A 是m×n 矩阵，秩为m，b 是m 维列向量，f（x）可行域记为：。

使用MATLAB对提出的模型编写代码并进行求解，求解过程为：

（1）给定初始可行点x（1），允许误差，令k=1；

（2）求解线性规划问题，得到最优解y（k）；

（4）从x（k）出发，沿方向x（k）—x（k）在连接x（k）和x（k）的线段上搜索，得到；

3 仿真分析

3.1 搭建仿真环境

选取德州市某交叉口作为研究场景，仿真场景分为静态场景与动态场景。

3.1.1 静态场景

经现场调查与测量，路口每个方向上均为3 个入口和2 个出口，进口道宽度为3.2m。处理后得到该交叉口的大致布局分布见图3。

图3 研究场景布局示意图

3.1.2 动态场景

该交叉口信号相位为典型的对称放行四相位交叉口，右转无限制，南北车流量较东西方向车流量大。收集该交叉口7：00-9:00 两个小时的交通量，计数周期为5min 一次，通过对数据的整理与计算，该交叉口高峰小时为7:30-8:30，高峰小时各进口道车流量见表1。

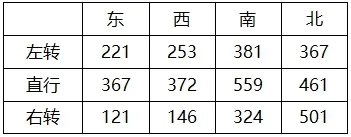
表1 车流量(单位：veh/h)

在对最大绿灯时间进行求解时，选取15min 内最大交通量作为高峰小时流量计算交叉口饱和度，按照表1所示的相位单侧高峰小时交通量分别为972veh/h、292 veh/h、1408 veh/h、1040 veh/h。求解后求得各个相位的最大绿灯时间分别为25s、20s、48s、26s。

3.2 通行能力分析

基于微观仿真软件进行标定，搭建网联车行驶状态下的模拟场景，通过仿真可以获得每个相位的平均有效绿灯时间与平均周期时长，仿真结果如表2 所示。

表2 仿真结果

根据公式（3）计算可以获得该交叉口在使用动态信号控制时的实际通行能力为3295veh/h。当交叉口流量增大时，会使有效绿灯时间倾向于固定值，此时采用动态信号控制并不能获得理想的效益。

4 结论

本文首先分析了网联车背景下信号交叉口控制原理，基于此分析了受动态信号控制时交叉口通行能力的计算方法，然后提出了确定最大绿灯时间与最小绿灯时间的方法，最后根据现场调查数据对仿真建模中的相关参数进行标定后进行仿真，经实例测试，提出的模型和方法是有效可行的。

本文提出的方法仅在交叉口流量不大时才会有显著效果，当交叉口流量较大时，动态信号配时会倾向于固定配时，在网联车环境下使更为灵活的控制方法成为可能，在下一步的研究中，将会对更为复杂的控制方法下的交叉口通行能力进行深入探究。