考虑周向波形特性的航空管路弯曲成形起皱理论建模与临界成形半径分析

刘 衡 汪志能,, 宾光富 林伟明 林姚辰, 马雁翔

1.湖南科技大学机械设备健康维护湖南省重点实验室,湘潭,4112012.浙江金马逊智能制造股份有限公司,丽水,3214003.浙江省航空航天金属导管塑性成形技术与装备重点实验室,丽水,321400

0 引言

航空管路制造缺陷严重威胁飞机服役安全性能。据相关资料,1965、1966两年间,我国某型歼击机由于管路缺陷产生的飞行事故占到失事总数的60%[1];2019年某公司一架空客A320飞机在起飞前,因管路问题导致飞行计划取消[2]。这些航空事故引起全球对航空管路缺陷的广泛关注。大量学者对航空管路缺陷进行统计,发现管路制造过程起皱缺陷出现概率极大。该缺陷诱发管路油液冲击、疲劳断裂,严重影响飞机服役的可靠性。为保障安全飞行,需严格保证航空管路制造无起皱缺陷。

管材起皱缺陷形成是一个非常复杂的弹塑性流动过程。大量工程实践[3-9]表明,起皱受弯曲半径的影响极大。文献[10]对钛合金管材进行弯曲极限研究,发现CP-Ti大口径薄壁管材(直径50.8 mm,壁厚0.508 mm)在弯曲半径小于101.6 mm时出现失稳起皱。文献[11]通过对弯曲工艺参数的研究和实验分析,采用数字分析和有限元建模仿真的方法,获得了0Cr18Ni9管材无芯冷弯成形极限。文献[12]对铝合金管材进行了起皱分析,实验研究了直径15 mm、壁厚1 mm的6061-T6管材在进行自由弯曲时的成形极限。为了解释弯曲半径对不同管材弯曲成形起皱规律的影响, 文献[13-15]采用有限元方法从力学机理上分析了起皱过程应力与应变。这些研究表明,管材起皱是一个应力做功与理论起皱能的平衡过程。一旦应力做功超过起皱能,管材流动失稳,就发生起皱现象。因此,要揭示弯曲半径对起皱的影响机理,需构建出精准的应力做功与起皱能理论模型。对于应力做功,部分研究人员将该应力功近似为管材弯曲过程外部电机的输入功,实际上电机输入功率不完全用于内侧管材压缩成形,还用于外侧管材拉伸成形。文献[16]基于中性层偏移理论分析了管材拉伸塑性变形区与压缩塑性变形区。在此基础之上, 文献[17]建立了压缩塑性变形区应力与应变理论模型,结合压缩塑性变形区面积、应力与应变模型,形成了应力做功模型。对于起皱能,其数值大小与管材起皱变形程度相关。文献[18]对板材弯曲起皱变形进行了研究,发现板材起皱在弯曲方向上呈余弦连续波动,在法向方向上呈线性衰减特性,并以此构建了弯曲方向连续波动与法向方向线性衰减的二维波形函数。结合该二维波形函数,文献[18-19]建立了矩形板弯曲起皱能函数,并较为精准地预测了矩形板起皱。文献[20-21]将该矩形板波形函数引入管材,建立了管材起皱能理论模型,在一定程度上对工程起皱预测起到了较好的指导作用,但仍存在预测精度不高的问题。实际上,管材起皱波形与板材起皱波形存在着较大的差异。大量工程实践表明,管材起皱仅在轴向上呈连续波动特性,在周向方向呈单峰波形特征。现有管材起皱理论模型大多没有考虑管材周向起皱波形特性。

为此,考虑管材周向起皱波形特性,本文对管材起皱波形特性进行了分析,提出了一种轴向连续波动、周向呈单峰波形函数分布的波形函数,构建起皱能理论模型,结合管材弯曲应力变化特性,建立了应力做功模型。依据能量准则,推导弯曲过程临界起皱判定依据,在此基础上,研究弯曲半径对管材成形中起皱的影响机制。

1 管材起皱理论建模

1.1 管材起皱波形函数构建

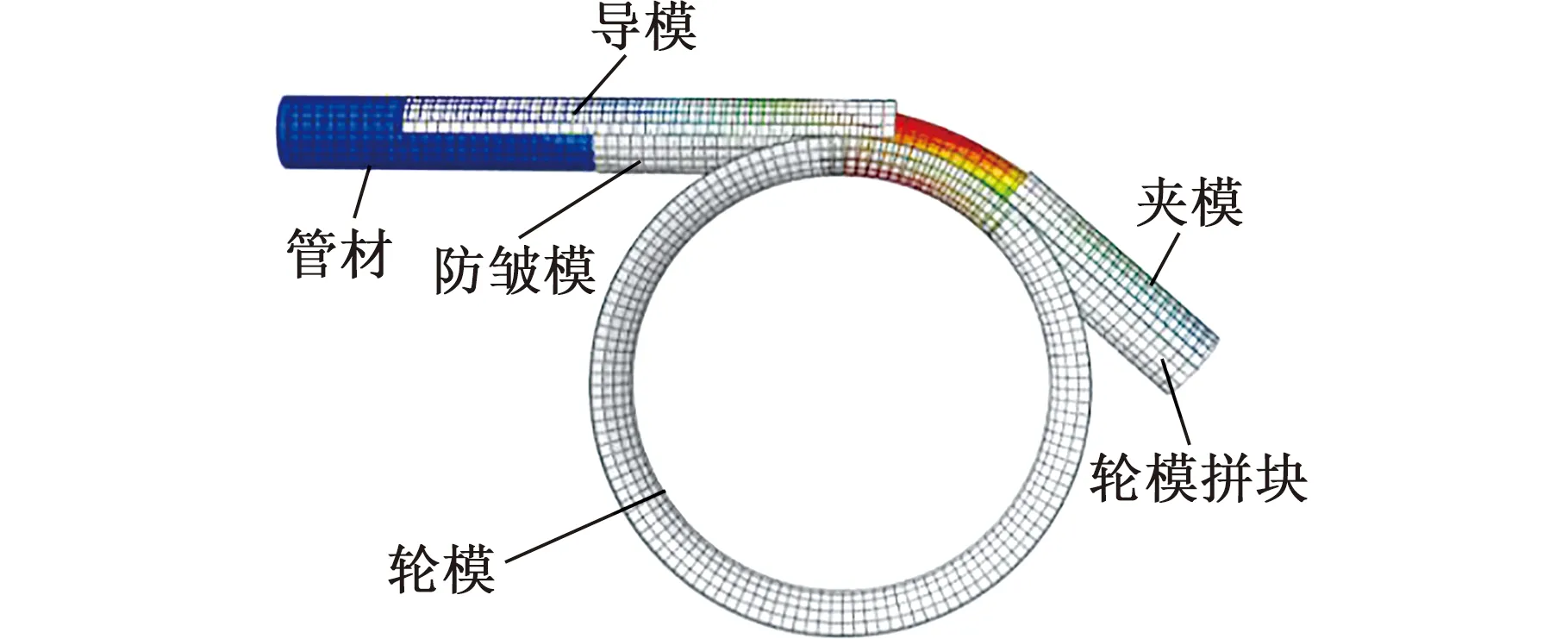
管材弯曲原理如图1所示,管材围绕轮模弯曲成形过程中外侧不断受拉,内侧不断受压。其中,管材中性层在弯曲过程中发生内移。在极限弯曲状态下,内侧受压材料流动易失稳,发生失稳起皱现象。

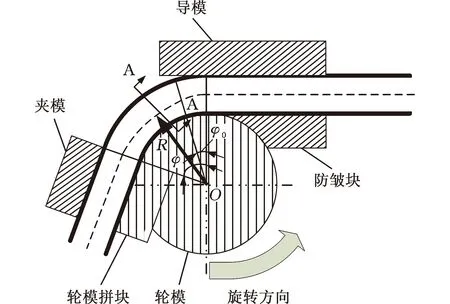
(a)弯曲原理示意图

(b)中性层偏移示意图图1 弯曲原理图及中心层偏移图

众多研究者[18-19]采用板材起皱波形函数描述管材波形特性:

w0=δ(b-y)sin(mπx/l)

(1)

式中,w0为板材起皱波形函数;δ为起皱的波高;b为起皱的宽度;m为半波数;l为起皱时投影在二维平面的弧长;x为板带长度方向上的位置;y为板带宽度方向上的位置。

板材起皱在弯曲方向上呈连续余弦波动特性,在法向上呈线性变化特性,而管材起皱波形与板材存在着较大的差异,其变化如图2所示,在周向上并非呈现矩形板的线性衰减特性。大量实践数据[20-21]表明,弯管在周向方向上呈单峰波形函数波动特性。通过有限元仿真获得管材弯曲成形起皱数据,管材相关仿真参数如下:管径30 mm,壁厚1 mm,弯曲半径100 mm。为研究管材起皱区周向波形特征,选取起皱区一个横截面,其周向厚度特性如图3所示。

(a)管材起皱实物图

(b)板材起皱实物图[18]图2 起皱实物图

图3 周向管壁起皱波线形和波形函数拟合图

为描述周向波动规律,在后续拟合处理时,将图3中的厚度波动数据减去了初始厚度值1 mm。从材料变形过程中质量守恒原理上讲,材料周向起皱波形与轴向起皱波形具有类似特征。实际上,大量研究已经证明管材起皱波在轴向呈余弦变化特性[22],那么,基于体积不变原理,周向波形也应呈余弦波动特性。为此,将起皱周向波形数据导入MATLAB拟合工具,通过自定义函数对数据点进行拟合,结合现有的轴向波动公式[18],可形成管材轴向-周向的波动函数:

(2)

R′=R-rcosα

式中,w为管材的起皱波形函数;R为管材的弯曲半径;α为圆周向角;r为管材的半径;φ为管材弯曲的角度;φ0、φ1分别为起皱区域外圆周起始角和最终角,一般地φ0=0°,φ1=90°(图 1)。

为对比传统的周向线性波形函数式(1)和新建的周向波动波形函数式(2)的拟合效果,对周向线性波形函数式(1)进行拟合:首先根据线性拟合曲线找到横坐标截距,该截距就是起皱的宽度b;其次,拟合曲线的纵坐标截距即为起皱的宽度与起皱的波高的乘积δb,根据起皱的宽度b,可计算获得起皱的波高δ。同样,可对新建的周向波动波形函数式(2)进行拟合。通过对比可知,有限元仿真数据与式(2)吻合精度极高,达到了99.8%。

1.2 起皱力学分析

管材弯曲过程应力分布如图4所示,基于力平衡关系[23],周向应力与轴向应力满足关系

(3)

式中,σx为轴向应力;σc为周向应力;ω为弯曲半径与管径的比值,ω=R/(2r)。

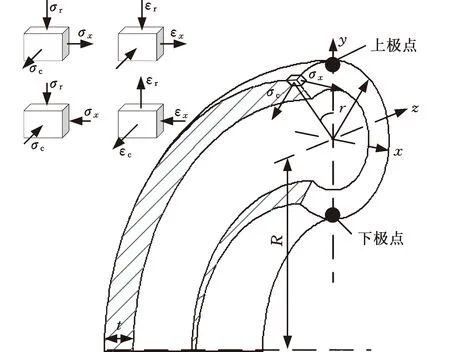
图4 管材弯曲的应力应变与几何参数

轴向应变可表示为

(4)

式中,εx为轴向应变;e为中心线偏移距离,e=0.42r/ω。

管材弯曲过程采用von Mises屈服准则[23],屈服函数为

(5)

由式(3)、式(5)可得

(6)

应力状态进入塑形阶段需用到增量理论[23],可表示为

(7)

式中,λ为正标量常数(与材料硬化有关);下标x、r、c分别表示轴向、径向、周向三方向。

依据式(3)、式(5)、式(7)可得

(8)

依据式(8)可以得到 3 个方向应变的比例关系:

εx∶εc∶εr=(2-ϖ)∶(-1-ϖ)∶(2ϖ-1)

(9)

依据式(4)、式(9)以及畸变能理论[23]可得等效应变

(10)

航空管材可选用幂强化材料模型[23]描述材料塑性流动特征:

(11)

式中,K为强度系数;n为硬化指数。

联立式(6)、式(10)、式(11),可求解管材弯曲过程轴向应力

σx=

(12)

同理,可求解周向应力

σc=

(13)

1.3 基于波形函数的管材临界起皱判定

管材在弯管成形过程中,塑性稳定流动状态的条件为:外力做功T小于材料内部起皱能U。一旦外力做功T超过起皱能U,管材将失稳起皱。

对于起皱区,外力做功量为

T=t∬|σx|r2cosαdαdφ

(14)

式中,t为管材厚度。

内部起皱能与波形函数相关。林艳[22]提出内部起皱能与波形函数满足如下关系:

(15)

式中,Es为割线模量;Et为切线模量;Er为折减模量;E、ν分别为管材的弹性模量和泊松比。

当管材弯曲90°时,根据最小能量原则,管材内能虚拟增量为

F=U-T=m2K1+K2+K3/m2

(16)

(17)

(18)

(19)

起皱判定条件为

(20)

此时管材不发生起皱,且临界波数

2 有限元验证

借助ABAQUS有限元软件,建立管材绕弯成形过程有限元分析模型。绕弯成形模具结构参数如表1所示。管材材料为LF2M,管材的材料模型采用幂强化材料模型,管材的材料参数如下:密度2700 kg/m3,弹性模量7600 MPa,泊松比0.33,硬化指数0.26,强度系数184 MPa。管材壁厚1 mm,管材管径在30～60 mm之间。设置弯曲模以 0.1 rad/s的速度转动90°。轮模拼块和夹模与轮模同步转动。导模以轮模的切向线速度19 mm/s沿管材移动方向移动。防皱模和芯轴保持静止,约束所有自由度,芯球不受任何约束,保留所有自由度。接触类型选择面面自动接触,接触算法为罚函数法,设置初始罚函数刚度因子为0.01。

表1 成形模具的结构参数

管材弯曲过程有限元模型和管材厚度分布规律如图5所示。为了验证新建理论模型的准确性,在保证所选的流动关系和屈服准则相同的情况下将理论模型计算结果和有限元仿真结果进行对比分析。相关计算参数为:管径30 mm,壁厚1 mm,弯曲半径60 mm。

(a)有限元模型

(b)厚度云图图5 有限元模型及厚度分布

对于新建理论模型,在已知材料参数和弯曲半径的情况下,根据式(4)、式(7)、式(9)可计算出管材轴向、周向以及径向方向的应变值。选取一个过起皱区的圆形横截面进行分析,对比理论模型计算结果和有限元仿真计算结果,如图6所示。轴向应变在管外侧为正,在管内侧为负,这表明管材在外侧受轴向拉伸,在内侧受轴向压缩。周向应变与径向应变表现出与轴向应变相反的变化规律,即在管外侧受周向和径向压缩,在管内侧受周向和径向拉伸。对管材内侧区域进行分析,越靠近弯曲半径方向的下极点,轴向压应变越大,即越靠近管内侧轴向压缩量越大。材料在轴向压缩过程中,同时会产生周向和径向拉伸效应,并且这种周向拉应变与径向拉应变越靠近下极点位置越明显。这说明材料在轴向堆积过程中,往周向和径向存在扩散效应。这种扩散效应在一定程度上对材料局部堆积具有一定的缓解作用。但相对于材料轴向堆积速度,材料往周向和径向方向的转移量有限,即材料往周向和径向扩散速度远不及轴向材料堆积速度,尤其是在靠近下极点位置,轴向压应变急剧增大,过快的材料堆积造成材料流动失稳,材料在局部区域过渡积累,引发内侧管壁起皱现象。

图6 应变的仿真与计算

3 实验验证

实验设备采用KM-A100-CNC-E120数控弯管机,如图7所示。夹模与轮模拼块将管材固定,夹模施加夹紧力,迫使复合管沿弯曲模中心线旋转。导模施加压力夹持在管壁上向前运动,提供助推作用。防皱模和轮模紧密相切,到达设定弯曲角度时完成整个弯曲过程。弯曲过程结束后,模具脱开。数控弯管机成形模具的结构和工艺参数具体如表1所示。设置轮模以0.1 rad/s的角速度绕转动中心转动,轮模拼块和夹模与轮模同步转动,导模以轮模的切向线速度沿管材移动方向运动。

图7 数控弯管机

为研究管材弯曲的成形极限,采用LF2M作为管材材料,弯曲起皱实验方案如表2所示。由图8可明显发现60 mm管径的管材在弯曲半径为113 mm时出现起皱情况。

表2 实验方案

图8 加工的管材

图9所示为弯曲实验临界弯曲半径Rc验证结果。根据周向单峰凸波波形函数的起皱理论模型,采用MATLAB编程计算,先输入已知参数管径、材料特性参数、初始弯曲半径等,然后计算式(1)～式(13)得到应力和应变,再通过式(14)～式(19)计算起皱能量和外力做功,最后根据式(20)的判别不断递增弯曲半径直到满足判别式(20),停止计算。传统模型采用周向线性衰减波形函数,与圆形管起皱波形存在着一定的差异。新建理论模型考虑了周向呈现出单波特性,其计算结果和实验结果误差在5.5%以内,较传统模型高出了12%,说明建立的成形起皱机理模型可以精准地预测起皱。

图9 实验与理论计算对比图

4 临界弯曲半径影响因素分析

在验证新建立的管材起皱理论模型的准确性后,分析典型影响因素对临界弯曲半径的影响。弯曲半径直接影响管材弯曲内侧部位应变量,对起皱能影响较大。图10所示为外力功T与起皱能U之比即起皱率(T/U)随弯曲半径变化规律(管径D=60 mm)。弯曲半径越小,管材内侧弯曲部位轴向压缩量越大,外力功亦急速上升,外力功与起皱能之比在小半径(75～100 mm)区域随半径减小表现出急剧增大现象。这意味着管材小半径弯曲时,其外力功能快速逼近材料的起皱极限,造成管材起皱失稳。

图10 弯曲半径对起皱率的影响

管径会影响中性层位置,大口径管材弯曲时,其中性层内移距离较小,内侧受压缩应力区域增大。图11a为起皱率随管道半径变化曲线。管径越大管材所需的弯曲力矩也越大,管材内侧受压区域应力上升,其外力功也增加,因此随管径增加,当外力功与起皱能之比逐渐增大。外力功突破起皱极限时,管材起皱。因此在实际生产过程中大口径管材弯曲成形半径不宜过小。对不同管径的管材临界弯曲半径进行分析,如图11b所示,管径越大,其临界弯曲半径越大,弯曲半径与管径成线性变化规律。根据管径与临界弯曲半径的线性变化特征,采用线性函数拟合,可得临界弯曲半径与管材口径的函数关系:

Rc=1.89D

(21)

对拟合式(21)进行验证,在其他工况下,如厚度t=0.5,0.8 mm的管材参数下,临界弯曲半径与管材口径也基本符合式(21)。对管径与临界弯曲半径的线性变化特性进行分析可知,管材弯曲半径不易过小,建议临界弯曲半径不小于1.89倍管道直径。

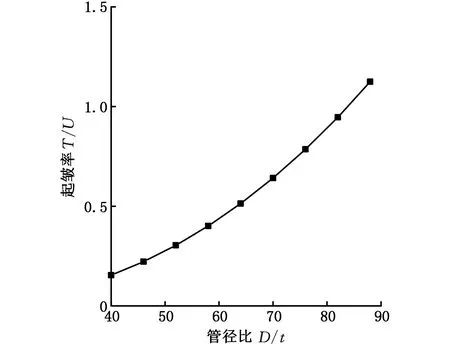
(a)管径比对起皱率的影响

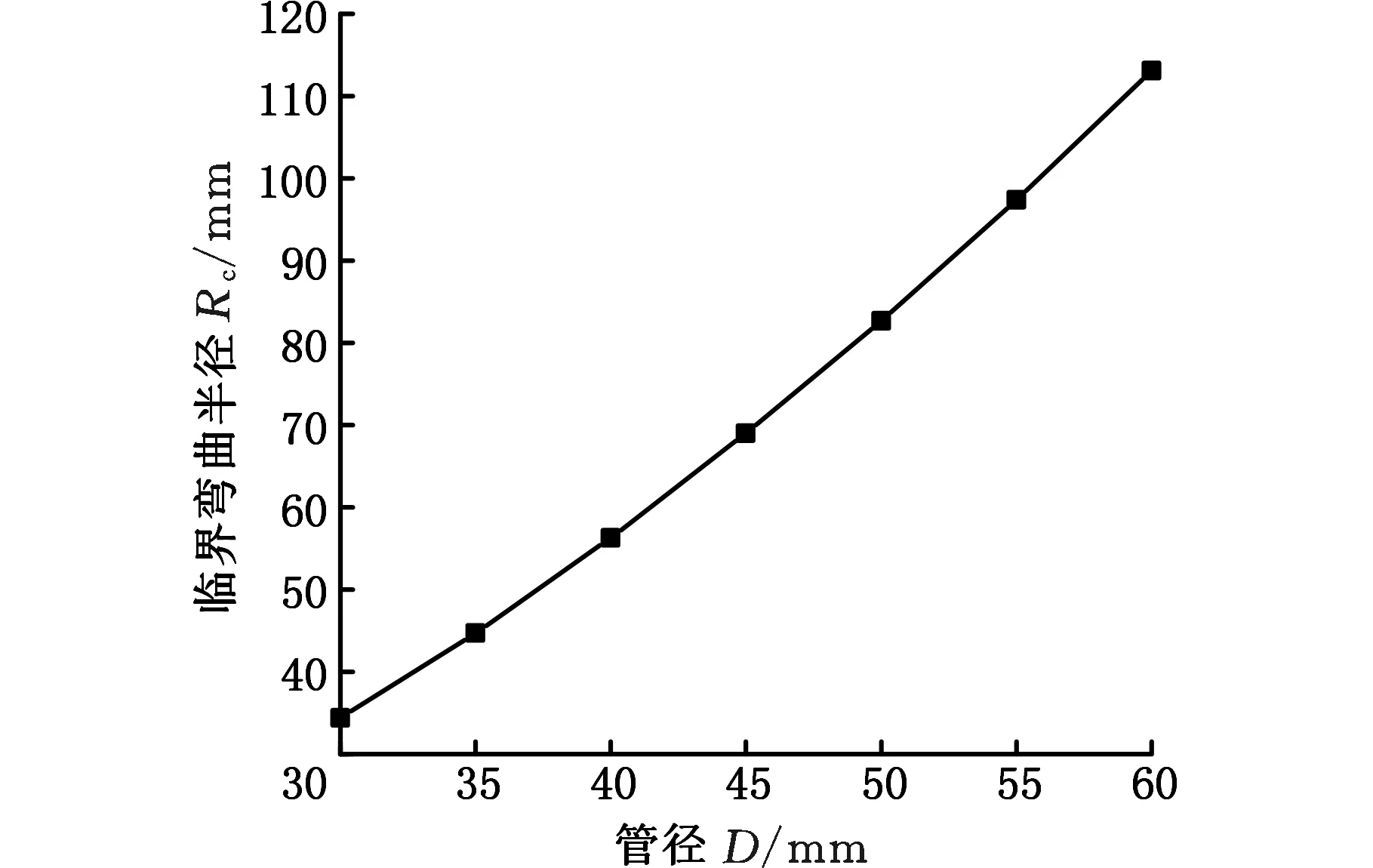
(b)管径对临界弯曲半径的影响图11 管径比的影响(t=1 mm)Fig.11 Influence of pipe diameter ratio(t=1 mm)

材料硬化指数对管材起皱的影响较为复杂。图12a为起皱率随材料硬化指数变化曲线。起皱率随硬化指数增加表现出先减小后增大的规律。其中,在低硬化指数区域(n<0.1)减小极为明显,这说明管材起皱在低硬化指数区域变化极为敏感。一般而言,硬化指数减小能显著降低管材弯曲加工硬化程度,但会造成压应力分布不均现象,诱发管材内侧压缩区域出现局部应力集中,同时这种材料软化效应会抑制管材材料向周向扩散,进一步造成材料在局部点出现过度积累,严重削弱管材的抗起皱能力,因此,起皱率在低硬化指数区域(n<0.1)表现出急剧下滑特性。当材料处于高硬化指数(n>0.4)区域时,起皱率随硬化指数的增加表现出快速增大趋势。这种过快的增大趋势同样也削弱了管材抗起皱能力。对于高硬化指数,材料强度随硬化指数呈指数增加,在弯曲加工过程中所需要的弯曲力矩增大,这直接造成起皱区外力功急剧增加,从而导致起皱率随材料硬化指数增加而增大的情况。对不同硬化指数下的管材临界弯曲半径进行分析,如图12b所示。临界弯曲半径的变化曲线与图12a中起皱率曲线表现出相同的趋势。当材料处于低硬化指数区域(n<0.1)时,临界弯曲半径随硬化指数的增加迅速减小,这进一步说明临界弯曲半径对低硬化指数极为敏感。同样,当材料处于高硬化指数(n>0.4)时,临界弯曲半径随硬化指数的增加也表现出急剧增大的特性。因此,工程上管材选取硬化指数不宜过小,也不宜过大,硬化指数的最佳范围为[0.1,0.4]。

(a)硬化指数对起皱率的影响(强度系数K=184 MPa)

(b)硬化指数对临界弯曲半径的影响(强度系数K=184 MPa)图12 硬化指数的影响

强度系数影响管材内侧塑性变形区域抵抗起皱的强弱程度。不同强度系数对管材起皱率的影响如图13a所示。起皱率随强度系数的增大而减小,但是变化幅度不大。增大强度系数,弯管材料对塑性变形的抵抗能力略有增强,但总体上强度系数对起皱能的影响并不明显,因此,起皱率随强度系数变化比较平缓。如图13b所示,在强度系数的影响下临界弯曲半径的变化没有超过0.2 mm。工程上,基本可忽略强度系数对管材内侧起皱缺陷的影响。

(a)强度系数对起皱率的影响(硬化指数n=0.26)

(b)强度系数对临界弯曲半径的影响(硬化指数n=0.26)图13 强度系数的影响

5 结论

(1)建立了基于周向单峰凸波波形函数的起皱理论模型。传统起皱采用周向线性衰减波形函数,与圆形管起皱波形存在着一定的差异。实际弯曲过程中,圆形管内侧轴向波表现出连续变化的特点,周向表现出单波特性。为此,建立起轴向连续波、周向单波波形函数,结合管材弯曲应力应变模型,推导了外力功与起皱能理论公式,基于外部能量过剩理论,形成了管材弯曲起皱判据公式,结果表明临界起皱判据方法预测精度达到了94. 5%,能为实际工程提供有力的理论指导。

(2)管材起皱对弯曲半径极为敏感。管材弯曲半径不宜过小,临界弯曲半径不小于1.89倍管道直径。管材弯曲起皱本质上是一种材料沿轴向、周向与径向三个方向的重分布过程。弯曲半径对材料三方向流动速度影响极为明显。过小的弯曲半径所需外力功较大,能急剧增加轴向压缩应变,造成材料在管材内侧局部区域轴向堆积严重,形成管材起皱现象,因此管材实际弯曲半径不宜过小,最小弯曲半径不应小于1.89倍管道直径。

(3)材料硬化指数对临界起皱半径的影响表现出复杂的非线性特性。工程上管材硬化指数选择宜适中,较佳的抗起皱硬化指数范围为0.1≤n≤0.4。材料硬化指数能提高管材应力分布均匀性,削弱内侧峰值应力,在一定程度上提高管材抗起皱能力,但过高的硬化指数增加了管材屈服强度,导致外力功急剧增加,管材更易起皱。因此,为了减少起皱失稳现象的发生,工程上管材选取硬化指数不宜过低,也不宜过高。