顾及视线效应的城市户外传感网络空间布局优化

张笑雨,马潇雅,2

(1. 长江大学地球科学学院,湖北 武汉 430100; 2. 自然资源部城市国土资源监测与仿真重点试验室,广东 深圳 518034)

城市户外空间由不同类型传感器构成的传感网络是智慧城市基础设施建设的重要内容[1-3]。城市中的部分传感器,如基于可见光的传感器和激光雷达等,其服务范围易受障碍物遮挡而导致其真实有效感知范围非常有限[4]。这种服务需求与传感器设备之间需要视距可见才能实现感知服务覆盖的特性,在设施选址问题中通常被定义为视线效应(line-of-sight,LOS)[5-6]。在传感网络布局规划中,决策者往往需要根据建筑物的形态与空间分布,在建筑物密集的区域部署大量传感器,以实现对重点区域的无缝服务覆盖[7-8]。以最小的设备数量和运营成本,实现有效服务范围的最大化,是城市传感网络空间布局优化问题的核心目标和主要难题[9]。

城市传感网络的空间布局优化问题从本质上是一类特殊的最大覆盖选址问题(maximal covering location problem,MCLP)。针对不同设施选址的应用场景,国内外相关学者先后对经典MCLP模型进行了改进。如文献[10]提出了基于欧式距离同心圆模式的通信基站服务覆盖模型;文献[11]设计了顾及任意凸多边形障碍物阻隔效应的设施选址模型;文献[12]设计了针对具有盲区的有向视觉传感器在保持连通性前提下的最大保持覆盖控制模型。

但顾及LOS服务覆盖特性的选址优化模型仍有待深入研究。如文献[13]提出一种顾及LOS效应的无线传感器网络优化模型,但该模型不适用于建筑物密集分布的城市复杂建筑环境。文献[14]提出了一种基于GIS视域分析方法的校园安全监控摄像头网络布局优化模型,但模型仅用于解决小区域内的选址优化问题,难以实现对大空间范围的监控传感网络的高效率优化。

本文提出一种基于可视多边形算法(visibility polygon,VP)[15]的城市户外传感网络覆盖模型。此外,MCLP问题是一类典型NP-hard问题[16-17],现有研究表明,以遗传算法(genetic algorithm,GA)为代表的启发式优化算法是解决这类NP问题的有效工具[18-21]。因此,本文将耦合遗传算法和GIS技术相结合,设计城市户外传感网络布局选址优化算法,并以某城市街区传感网络中的摄像头空间布局优化问题为例,对设计算法的有效性进行验证。

1 顾及LOS效应的传感网络布局优化建模

1.1 顾及LOS效应的传感器服务覆盖模拟

假定传感网络中布设的传感器在没有障碍物阻隔效应的情况下,对于给定有效服务距离R,其在二维空间内的服务覆盖范围是一个以传感器为中心,半径为R的理想圆[22]。然而,由于城市内不规则分布建筑物的阻隔效应,传感器的实际有效服务覆盖范围是一个不规则的多边形(如图1(b)所示)。对于任意给定地理坐标的传感器部署候选站点x和建筑物分布集合,利用VP算法和GIS获取其真实服务覆盖范围的基本步骤如下。

图1 顾及LOS效应的传感器服务覆盖范围建模

(2)传感器站点的可视范围生成。根据候选站点x的点位、理论覆盖圆和圆形内的建筑物分布、形状,利用VP算法生成候选站点x对应的可视多边形。其基本思路为:以x为中心,以圆形区域内的建筑物拐点为终点,生成系列视线,若视线遇到障碍物或圆形边界,且视线不与任意障碍物相交,则生成一个视线端点。该端点即为视域范围的轮廓点,按照顺时针方向连接各端点即可生成可视多边形(如图1(b)所示)。关于VP算法更多详细的情况可参考文献[15]。

考虑相邻传感器设备之间LOS服务覆盖可能存在重叠情况,在生成单个站点的可视范围后,利用GIS的多边形合并(Union)功能,将多个站点的独立可视多边形融合成单个多边形。图1(b)—(c)中的蓝色多边形区域分别为传感器站点x和y独立生成的可视服务范围;图1(d)则展示了规划区域中被传感网络站点x和y最终覆盖的区域。

1.2 传感网络布局优化问题的定义

二维场景下的传感网络布局优化问题主要包括对服务覆盖需求、建筑物集合和候选站点集的建模。本文服务覆盖需求可用连续多边形进行表达,建筑物则使用二维多边形表达。

获取候选站点时,首先利用GIS叠置分析方法,排除空间上不适合布设监控站点的区域(如坑塘水面、建筑物、河流等)。利用系统抽样方法按照固定间距对可部署的候选区域进行抽样[13],从而有效降低算法搜索空间。

基于给定的采样间距d,对可部署区域进行抽样,d越小,则采样和优化算法的寻优结果精度越高;反之,则精度越低。随着采样间距的降低,算法寻优耗费的时间呈指数上升。如图2所示。

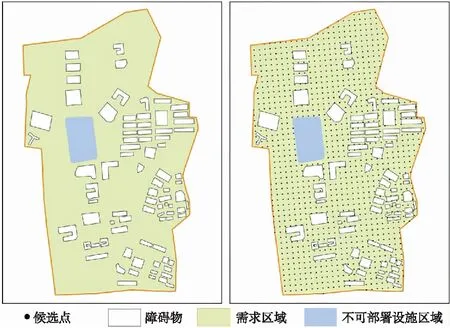
图2 候选站点提取原理

根据上述原则,给出优化问题的变量约定如下:对于面积为SA的多边形规划区域A,通过系统抽样方法获取了由N个点构成的候选站点集合C。假定计划在区域A部署P个传感器,每个传感器设备的有效服务视距为R。从候选站点集合中选取P个位置,可获得优化问题的一个可行解SL。

对可行解SL中的任意站点i,可利用VP算法获取其可视多边形V(i)。则范围A内所有被可行解SL内P个站点覆盖的多边形区域LOSV定义为

使用训练得到的转移概率矩阵和风险概率临界值可以识别异常交易行为，以第二章中提到的短信支付流程为例，正常交易序列间的概率和黑客交易序列间的概率如图6 所示，其中每个节点为从日志中提取的每一步交易名称，节点间的值为交易间转移的概率。

LOSV=∪iSLVi

(1)

式中,区域内最终被所有站点覆盖的区域LOSV是所有可视多边形V(i)覆盖区域的并集,可利用GIS的多边形求并方法获取。

按照以上约定,研究提出的顾及LOS效应的传感网络布局优化问题定义为

Maximize: SC=(SLOS×100)/SA

(2)

Subject to

(3)

式中,SC为整个规划区域内被传感网络站点直接视线覆盖的面积占比;SLOS为多边形LOSV的面积;式(2)定义了问题的优化目标,即对于给定数量的传感器站点,实现其LOS覆盖范围的最大化;式(3)用于确保整个候选站点集合C中有且仅有不重复的P个站点被选中。

2 城市传感网络布局优化方法

2.1 遗传算法的优化流程

遗传算法寻优能力强、算法框架灵活,目前已广泛应用于空间设施选址优化领域[17,23-25]。经典的遗传算法流程如图3所示。

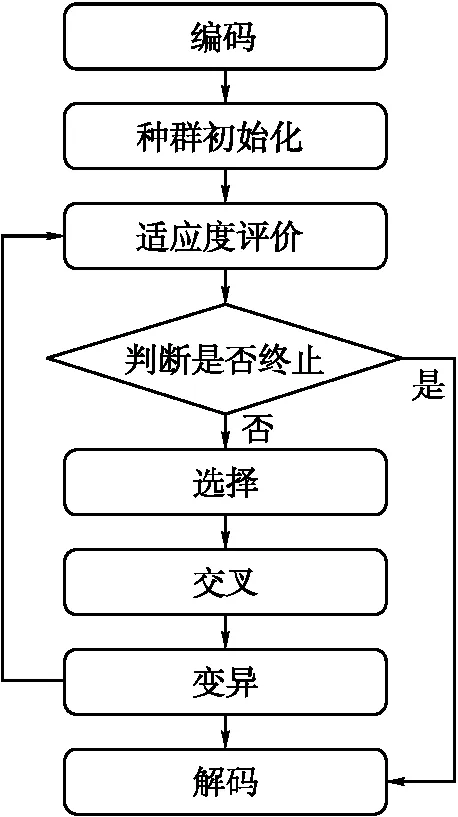
图3 遗传算法的基本流程

遗传算法步骤通常为:①编码。通过一定的编码方案,将现实世界问题的决策变量逐个映射为基因;现实世界问题的一个可行解即对应遗传算法中的一个染色体,构成算法的基本进化单元。②种群初始化。根据编码方案和给定的种群规模,随机生成第一代染色体种群。③个体适应度评价。通过给定适应度函数评估种群内每个染色体的适应度。适应度高的染色体表明该染色体对应可行解的质量越优。④终止条件判断。判断算法是否达到最大迭代次数或是否已收敛,若满足其中任意一个条件,算法则终止并执行步骤⑧,否则执行步骤⑤。⑤选择。通过“轮盘赌算法”随机选择双亲个体遗传下一代,适应度值越高的个体被选中的概率越大,从而实现染色体的“优胜劣汰”。⑥交叉。两双亲染色体的基因在同一位置处切断其基因链,并相互交叉重新组合为两个后代个体。⑦变异。将个体基因链中的基因用其他随机选择的新基因替换,从而生成新一代个体,继续执行步骤③。⑧解码。输出染色体种群中适应度最高的个体作为优化问题的最优解以辅助决策。循环执行步骤③—⑦,直至满足步骤④的终止条件。

2.2 面向城市传感网络空间布局优化的遗传算法

为耦合GIS技术以求解传感网络布局优化问题,经典遗传算法的编码方案、个体适应度评价、交叉和变异算子需要针对问题的特点重新设计。

(1)编码。对候选点集C中的每个站点进行整数编码,为每个候选站点分配整数作为其唯一的ID。对于任意给定数量的P个待部署站点,其可行解对应的染色体可用一条长度为P的整型数组进行表达。染色体中的每个基因存储了其对应站点在集合中的整数编号。

(2)个体适应度评价。对于任意给定以整型数组表达的染色体,根据其整数编号找到其在集合C中的地理坐标,并在GIS的支持下,利用VP算法和式(2)—式(3)定义的目标函数计算每个染色体的适应度值。

(3)交叉。通过轮盘赌策略选择两个父代染色体后,根据给定的交叉概率Pc在染色体上随机选择一个交叉点。位于交叉点后的两个父代染色体互相交换基因值,从而产生两个新的染色体(如图4(a)所示)。为了满足式(3)定义的约束条件,若染色体中出现了两重复的候选站点编号,则对该染色体实施修复操作:去掉重复的编号,从候选点集中随机选取一新染色体代替。

图4 交叉与变异操作

(4)变异。根据给定的变异概率Pm实施变异操作时,随机从候选站点集合C中选择一个不存在于当前种群中的站点以替换当前基因的站点编号(如图4(b)所示),从而实现染色体的变异。

3 实证研究

3.1 试验设计

以某城市街区公共区域摄像头布局优化问题为案例,研究区总面积约为36.7 hm2,区域范围内建筑面积密度约为0.37,研究区及建筑物形状分布如图5所示。

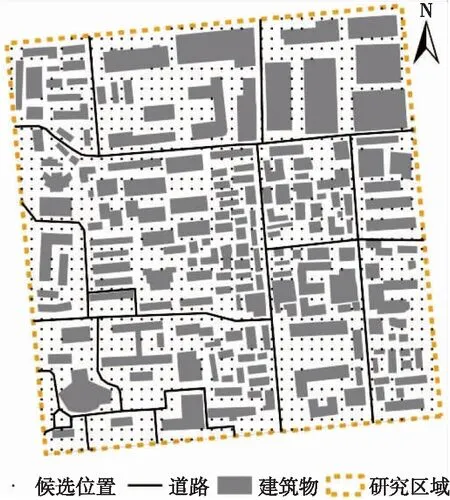
图5 研究区域

排除建筑物等不适宜部署区域后,按照15 m的采样间距,在研究区利用系统抽样方法获得995个摄像头站点布设候选点。在该区域布设有效监控视距为40 m、360°旋转的监控摄像头。监控网络布设的目标为覆盖整个街区面积的90%。P的初始值设置为80,试验时P值逐次增加5,直至P=150。确保每次试验算法都能收敛,设置算法最大迭代次数为2000,种群规模为100。交叉概率设置为0.8,变异概率设置为0.08。具体参数配置见表1。

表1 遗传算法参数配置

3.2 试验结果

基于试验区数据和表1设置的算法参数,通过多次运行优化算法后,获得试验区不同数量下的监控摄像头网络最优服务覆盖率和空间分布,如图6—图7所示。

图6 不同摄像头设施数量下的最优服务覆盖率

图7 LOS服务覆盖范围

当研究区内部署的设施数量分别为80、120、150时,由算法获取的最优服务覆盖率分别为74.67%、90%和 95.74%。总体上看,随着区域内部署监控摄像头个数的增加,所能有效覆盖的区域也随之稳步增大。然而,当站点个数超过120个时,通过增加站点个数提升覆盖比率的趋势有所放缓。

图7中,当P=80时,优化算法倾向于将摄像头站点布设于建筑物稀疏分布的开阔区域,从而获得更好的服务覆盖效果;而在建筑物密集分布的区域布设同等数量的设施可获得的有效服务覆盖明显低于开阔区域。因此,当P太小时,在建筑物密集分布的区域出现了大量的监控服务盲区(图7(a)中A、B和C空白区域)。而随着站点数量的增加,越来越多的摄像头站点被布设到建筑物密集分布的区域,以减少监控盲区。站点的空间分布和建筑物的分布状况存在明显的相关性。从图7(a)—(h)可以看出,随着P值的增加,图7(a)中位于建筑物密集分布区的大片监控盲区逐渐缩小,直至彻底消失(图7(h)中D和E区域)。由此可见,本文设计的传感网络布局优化算法能够有效地提高网络的实际服务覆盖范围。

考虑试验区的监控服务覆盖率目标和摄像头监控网络布设、运营成本,结合模型获取的优化方案,综合确定当P=120时,图7(e)中的摄像头布局是一种合理可行且具有较好经济效益的监控网络布设方案。

3.3 LOS效应对优化方案质量的影响

为进一步评估网络布局优化时,考虑LOS效应的必要性,研究设计了一个未考虑LOS效应的对比试验。将建筑物集合从模型运行数据集中移除,即可直接模拟未考虑LOS效应的监控网络布局优化场景。在对比试验中,将设施数量P初始值设置为70,其他算法参数设置与参照试验完全一致。未顾及LOS效应的监控网络布局优化结果分别如图8、图9所示。

图8 LOS效应对设施服务覆盖范围的影响

当数量为70时,在不考虑LOS效应的情景下,算法获得的理论最优服务覆盖率已达85.49%;而受LOS效应的影响,该方案对应的实际有效监控服务覆盖率仅36.08%。在未考虑LOS效应的情景下,理论上仅需约80个监控摄像头即可实现对试验区内90%以上的区域进行覆盖。而在LOS效应的影响下,其真实有效的LOS监控覆盖率仅为40.14%,比理论覆盖率低52.31%。在不考虑LOS效应下,随着区域部署摄像头个数的增加,其理论监控覆盖比率稳步上升。而由于受到LOS效应的影响,其对应的真实LOS监控服务覆盖比率呈现出一定的波动性。

此外,由图9可知,在不顾及LOS效应的场景下,优化算法倾向于在研究区内均匀地选取备选站点,导致所获得的优化方案存在大量的监控服务盲区。因此,在选址优化模型中实现对LOS效应的模拟仿真,对于传感网络布局优化十分必要。

4 结 语

城市传感网中,如摄像头等类型的传感器需直接视距可见,方能实现有效覆盖的特殊服务覆盖性,而利用现有各类基于MCLP模型的方法难以满足传感网络空间布局优化的需要。针对该问题,本文提出了一种基于可视多边形算法的传感器服务范围建模模型,实现了对顾及LOS效应的传感器站点有效覆盖范围的模拟仿真。耦合GIS和遗传算法完成区域传感网络空间布局的优化。最后,以某城市街区传感网络中的摄像头空间布局优化问题为例,验证了优化模型的有效性。

试验结果表明,本文提出的模型能够有效提高传感网络的真实空间服务范围。另外,对比试验结果表明,在不顾及LOS效应情景下,优化模型倾向于在研究区内均衡的布设监控摄像头站点。然而,由于建筑物对监控范围的限制作用,由此获得的优化方案其真实有效服务覆盖比理论服务覆盖范围低达52.31%。因此,在传感网络布局优化过程中顾及传感器服务覆盖的视线效应是非常必要的。

本文设计的顾及LOS效应的传感网络布局优化模型,对于其他具有相似服务覆盖特性的设施网络布局优化具有非常重要的借鉴意义。如路灯、智慧城市Wi-Fi热点、5G通信基站等。后续研究将关注具有类似LOS服务覆盖特征的设施网络优化。