众源空中全景影像位姿的透视变换解算方法

蒲泓亦,李 锋,徐 铮

(信息工程大学,河南 郑州 450001)

空中全景是利用旋翼无人机在空中悬停拍摄实景影像,对影像进行融合处理制成的全方位全视角实景地图,可将观察视角从地面转移到空中,实现从地平线到地平线的全景观察,获得空中俯视、遨游天空的体验感,对空间环境整体信息的掌握意义重大。国内区域可根据任务需要实地拍摄获取空中全景数据,但受国际关系和法律法规制约,境外陌生地域尤其是敌对国家或地区无法实地拍摄获取全景数据。随着无人机技术的普及,国内外无人机航拍爱好者利用消费级无人机在高空拍摄全景影像,并上传到网络平台供大众浏览。这些众源空中全景影像包含城市、海岸、港口、政府机构等目标信息,对境外战场环境勘察有重要意义。但由于缺少准确的地理位置和方向信息,众源空中全景影像无法在地理空间中精确定位定向和融合匹配,限制了其应用场景。

针对全景影像获取与应用问题,国内外已展开了大量研究。根据全景相机的成像原理,全景模型大致分为严格球面全景模型和理想球面全景模型[1-2]。严格球面全景模型强调全景成像过程中多镜头投影中心存在偏移和旋转,采用旋转矩阵和平移向量构建统一的球面全景坐标系。基于此模型的多镜头全景相机被应用到车载移动测图系统中,系统利用GPS+IMU提供的辅助数据平差计算球面全景影像位姿参数[3-4]。除了辅助地面载体进行测量外,全景影像逐步应用到无人机摄影测量工程实践中。无人机全景倾斜摄影测量将空中全景影像投影至立方体表面,对立方体表面的影像实施空中三角测量,重建场景三维模型[5]。全景摄影测量则是以理想球面全景模型为基础进行测量,属于近景摄影测量,主要用于建筑物三维重建[6-7]。算法方面,球面全景影像的快速位姿估计算法EPnP(efficient perspective-n-point)利用虚拟控制点表示像点和物方点,求得虚拟控制点的像空间坐标和物方空间坐标,根据欧式变换不变性解算影像位姿参数[8]。点-线特征联合算法融合影像上点、线特征的解算数学模型进行平差,求解位姿参数[9]。基于双球面投影的相对定向-绝对定向影像位姿估计方法,利用双目视觉原理计算视差,构建可量测球形立体全景模型[10-11]。文献[12]提出了适合球面全景成像特点的相对定向计算流程,结果符合摄影测量标准。当前,国内外全景影像位姿估计的大部分研究方法需要借助GPS+IMU辅助数据,增加方法成本和计算复杂性,在众源空中全景影像位姿解算方面尚无成熟的方法。

针对众源空中全景影像缺少位姿参数的问题,本文提出基于透视变换的众源空中全景位姿解算方法。根据空间后方交会原理和球面模型特征,设计基于透视变换的空中全景位姿估计算法,提出解算流程;重点研究“平-球-平”变换中模型和坐标变换,采用虚拟平面影像外方位元素描述全景姿态;依据透视变换的变形特征,设计顾及误差的迭代重加权最小二乘法,并通过案例验证方法的可行性和可靠性。

1 算法原理与步骤

1.1 算法原理

空间后方交会法根据成像特征建立共线条件方程,利用泰勒展开线性化方程,采用最小二乘法迭代求解6个外方位元素(XS,YS,ZS,φ,ω,κ)。其中,前3个是线元素,确定像片及其投影中心在物方空间坐标系中的三维坐标;后3个是角元素,分别为偏角、倾角、旋角,确定像空间坐标系三轴在物方空间坐标系中的方向。普通影像的数学模型为垂直于像空间坐标系z轴的平面,像点z轴坐标为定值:z=-f。球面全景像点的z坐标随像点位置的变化而变化,直接代入公式会增加变量,加大解算的复杂程度。本文提出的方法使用透视变换将球面全景模型转换为虚拟平面影像模型,通过解算虚拟平面影像外方位元素求得全景影像位姿参数,简化模型复杂度。方法核心为两个变换。

(1) “平-球-平”模型变换。平面全景模型是众源空中全景影像的原始模型;球面全景模型由平面全景模型球面建模得到,其位姿参数是方法解算的根本对象;虚拟平面影像模型是球面模型经球心透视变换产生的平面,作为连接球面像点和地面控制点的桥梁,其位姿参数是算法解算的直接对象。

(2)坐标系变换。利用旋转矩阵和平移向量将像点和控制点的坐标系转换为虚拟平面坐标系。具体转换过程如下:像素坐标系向虚拟平面像空间坐标系转换;地理坐标系向重心东北天坐标系转换;重心东北天坐标系向虚拟平面像空间坐标系变换。

考虑到透视变换的变形特征、控制点选择误差及测绘数据测量误差,方法在约束平面全景像点选择范围的基础上,设计顾及误差的迭代重加权最小二乘法解算全景位姿,以提高算法准确性和稳定性。

1.2 解算流程

与实拍空中全景影像不同,众源空中全景影像一般仅含有摄站所在县市和景区的名称属性或摄站大致的地理位置信息。由于解算位姿的前提是已知一定数量的地面点物方空间坐标和对应像点像空间坐标,设计历史测绘数据辅助的众源空中全景位姿解算流程,如图1所示。

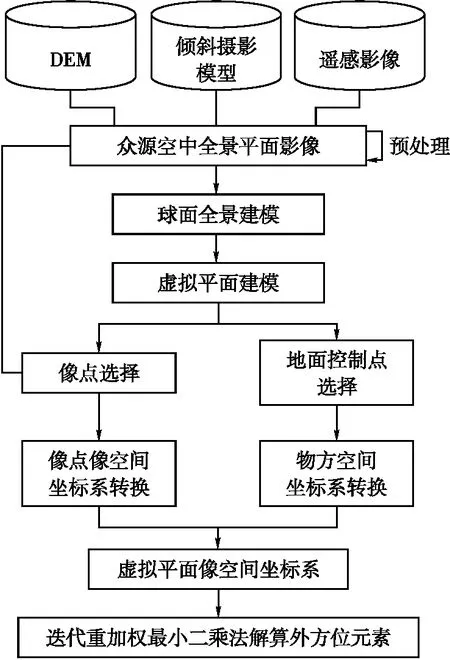
图1 解算流程

步骤1:基于遥感影像、DEM和倾斜摄影模型构建三维地理环境,作为全景影像粗定位的地理空间。

步骤2:获取众源空中全景影像,筛选成像质量较好的空中全景影像,预处理长宽分辨率比达到2∶1。

步骤3:进行球面全景建模。使用透视变换,将球面影像变换为虚拟平面影像,建立虚拟平面坐标系。

步骤4:在三维地理环境中选择地面控制点,确定对应像点。

步骤5:进行像点和地面控制点坐标系变换,将两者统一到虚拟平面坐标系。

步骤6:使用迭代重加权最小二乘法解算众源空中全景影像位姿。

2 空中全景变换

2.1 球面全景建模

球面全景是将平面全景影像映射到球面上得到的球面影像[13],原理如下:以影像中心O′为原点,U′轴平行于像素坐标系U轴方向相同,V′轴平行于V轴方向相反,构建辅助像素坐标系。像素点P′像素坐标(u,v)与辅助像素坐标系下坐标(u′,v′)的转换关系为

(1)

式中,l和w分别为平面全景影像的长和宽,比值为2∶1。

如图2所示,采用等距圆柱投影将平面全景影像映射至球面时,平面全景影像长和宽分别覆盖球面的经度和纬度,即[0,l]对应球面经度[-π, π],[0,w]对应球面纬度[-π/2, π/2]。以球心OS为原点,X轴指向O′,Y轴垂直于X轴构成球赤道平面XOSY,Z轴与X、Y轴构成右手坐标系,建立球空间坐标系OS-XYZ。从Z轴正方向看,顺时针球面经度为负,逆时针为正。球面投影点PS球面经纬度(α,β)与点P′辅助像素坐标(u′,v′)变换关系为

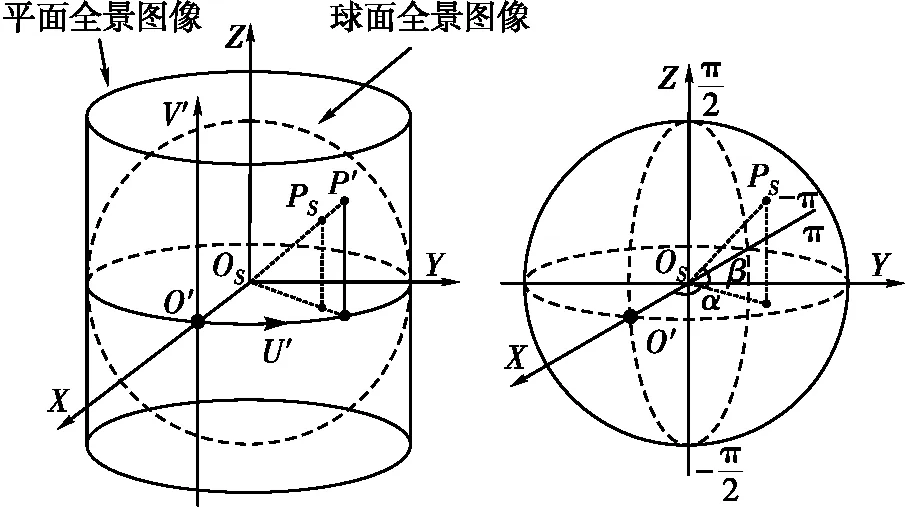
图2 球面全景建模

(2)

2.2 全景模型变换

空间后方交会法根据成像特点构造的共线条件方程为

(3)

式中,(x,y,z)为像点的像空间坐标;f为相机焦距;(X,Y,Z)为控制点物空间坐标;ai、bi、ci(i=1, 2, 3)为角元素的三角函数代数式。在球面全景影像中,像点PS的z值随像点球面纬度变化,并不符合经典空间后方交会的解算条件,通常的改进方式是同时列出x、y、z的方程,大大增加计算成本。本文对球面全景模型进行“球-平”模型变换,即利用透视变换将球面全景影像映射到虚拟平面,得到虚拟像平面像点,采用平面空间后方交会法进行计算,降低计算量。

如图3所示,设球空间直角坐标系Z轴负方向与球面交于点O1,过点O1并垂直于Z轴构建切平面xO1y。球面像点PS(α,β)和虚拟平面映射点p(x,y,z)连线方向交地面于点P。点PS与点p映射关系为

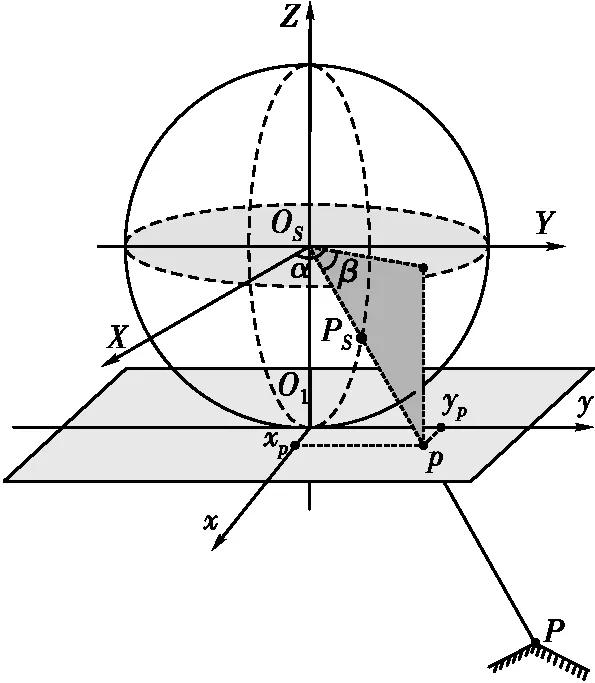
图3 全景模型变换

(4)

根据上述模型构建原则可知:虚拟平面影像的外方位元素与球面全景影像的位置和姿态相同,即可以采用虚拟平面影像的外方位元素描述球面全景影像位姿。

3 空中全景位姿解算

3.1 建立物方空间坐标系

(5)

式中,L和B分别为重心P0的经度和纬度。

3.2 加权重迭代最小二乘法参数解算

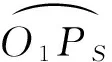
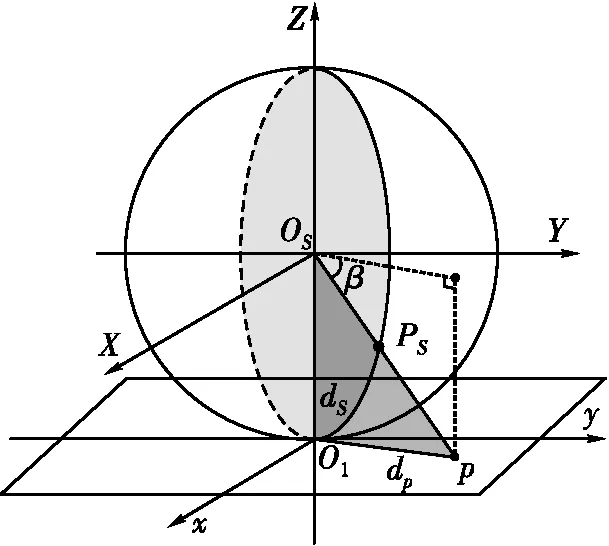
图4 “球-平”模型变换示意图

(6)

(7)

(8)

根据式(8)可知,变换前后长度产生变形。对Δd求导可知:当β∈[-π/2,0]时,β减小,Δd减小且变化速率降低;β增大,Δd增大且变化速率增大,即

(9)

(10)

(11)

式中,Δd′为Δd的导数。极点O1处长度变形为0,赤道处单位弧长与虚拟平面投影长度的差值为无穷。式(9)说明:对球面全景模型下半球进行透视变换,实际得到一个垂直于Z轴且过极点O1的超平面。将遥感影像、DEM和倾斜摄影模型作为控制点选取空间,控制点的坐标数据不可避免地包含了测量误差,其数值大小通常不一致。同时,人工选择像点的过程会引入偶然误差,尤其是选择赤道附近像点时,单位像素的偏差将引起虚拟平面像点极大的偏移,对位姿参数求解产生较大误差。因此,“平-球-平”模型变换对控制点对(像点和对应地面控制点)的质量提出更高要求,控制点对数目和分布都会对解算结果产生较大的影响。为尽量减少偶然误差,方法设定选取像点的纬度区间为β∈[-π/2,δ](-π/2 <δ<0)。

尽管通过限制像点选择范围降低了偶然误差,但仍然存在结果不准确的现象。经典的空间后方交会认为每个控制点对解算结果的贡献度相同,然而对于从历史测绘数据中选取的控制点坐标,其测量误差的分布与大小未知,如果不区别直接进行相机位姿估计,可能导致估计结果与真值相差甚远。因此采用顾及误差的迭代重加权最小二乘法解算众源空中全景影像位姿参数,以达到提高高质量控制点贡献,降低低质量控制点贡献的目的。在已知外方位元素近似值的情况下,按照式(3)一对控制点能够组成2个方程式。理论上,利用3个不在同一直线上的平高控制点即可解算位姿参数近似值的改正数。实际计算中一般选取4对或4对以上控制点,计算过程如下。

误差方程式矩阵形式[15]为

AX-L=V

(12)

其中

(13)

(14)

(15)

式中,A中元素由3个角元素决定;X为外方位元素改正数向量;L中lx=x-x计,ly=y-y计;V为误差向量。

迭代重加权最小二乘法的目标函数为

(16)

解算外方位元素改正数为

X=[ATWTWA]-1ATWTWL

(17)

式中,W为权值矩阵,每次迭代需不断更新矩阵元素wi。

式(12)是线性化近似公式,因此必须采用逐次趋近的迭代计算。将前一次改正的位姿参数作为近似值,重复建立误差方程求解,利用Xi(i=1,2,…,n)不断纠正位姿参数,直至改正数的绝对值小于阈值,或像点坐标的测量值与计算值之间的差值小于规定限差。

3.3 权值选取

权值分配在控制点的测量精度这一问题上应该遵循控制点的可信度原则,通过权值的分配调整异常值对整体误差的影响[16]。采用改进的Huber函数[17]确定权重矩阵元素wi,既能够快速收敛,又能够平衡异常值对整体计算的影响。以每一次迭代中虚拟平面上的像方残差为量度,根据残差大的点所对应的测量误差和深度影响剧烈这一特点可得权重系数的表达式[18]为

(18)

4 应用案例及分析

以河南省登封市纸坊水库地区的空中全景影像为案例对本文方法的有效性进行验证。试验采用全国底层遥感影像、DEM数据及纸坊水库倾斜摄影模型建立虚拟地理环境。全局坐标系采用WGS-84坐标系,参考椭球长半径a=6378 137 m,短半径b=6 356 752.314 2 m,扁率e=1/298.257 223 6。

从720云网址下载河南省登封市纸坊水库地区的多张空中全景影像,分辨率为8192×4096像素。由于地面控制点极少情况出现在影像上半球,且需要限制控制点选择范围,设定纬度区间β∈[-π/2,-π/4],即像点坐标分布在[0,8192]×[3072,4096]范围。设摄站初始高差Z0=50 m,等效焦距f=28 mm,阈值为0.001°。图5(a)以水库全景影像为例,说明了选取地面控制点并完成计算的过程,所选控制点见表1。

表1 控制点对坐标

图5 计算步骤和效果

计算得到全景影像外方位元素为

依据外方位元素,得到全景影像的地理坐标为(*** .525 093°N,*** .105 866°E,*** .36 m)。如图5(b)所示,根据所得到地理坐标和角元素,将全景影像融合至虚拟地理环境内,发现影像定位在准确位置,且进入全景前后虚拟相机视线方向保持一致,说明了本文算法的可行性和准确性。

在验证算法准确性的基础上,本文对算法的复杂度进行测试,使用迭代次数作为指标。试验中,控制点数目从6增加至16,步长为1,比较本文算法、球面后方交会算法[19]和球面迭代重加权后方交会算法收敛至阈值内的迭代次数(如图6所示)。其中,球面迭代重加权后方交会算法根据成像特点构建x、y、z的共线条件方程,采用迭代重加权最小二乘法解算。

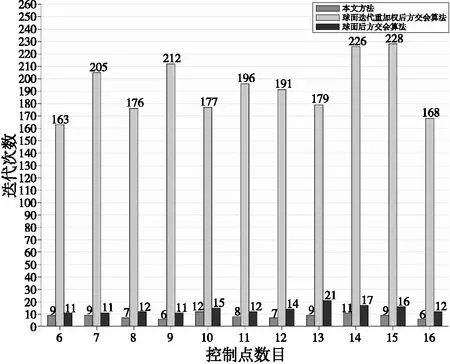
图6 算法迭代次数对比

由图6可知,与球面后方交会算法和球面迭代重加权后方交会算法相比,本文方法在有冗余控制点时,明显减少了算法的计算量。

5 结 语

解算影像位姿参数是众源空中全景影像应用于境外战场环境勘察的基础。本文提出了一种基于透视变换的众源空中全景位姿解算方法,设计完整解算流程;采用透视变换简化数学模型,着重阐明模型变换和坐标变换,减少了位姿解算计算量;使用顾及误差的迭代重加权最小二乘法解算位姿参数,增强了方法的稳定性。最后,以登封市纸坊水库众源空中全景影像为例进行验证。试验表明,本文方法能够实现众源空中全景影像位姿解算;存在冗余控制点情况下,既能减少计算量又能保持较高的稳定性。研究成果为众源空中全景影像与地理信息空间融合等应用提出一种新的实现方法,为境外战场环境勘察提供重要参考。