基于效用理论的未定权益最优套期保值策略
郭建华
(邵阳学院 经济与管理学院,湖南 邵阳,422000)
1 问题的提出
未定权益是一个非负可测的随机变量,作为终止时刻支付的协议。目前,越来越多的公司和企业采用支付未定权益的方式进行员工激励。股份期权就是非上市公司运用股票期权进行员工激励的一种模式。管理人员经营业绩考核和资格审查后可获得一种权利,即在将来特定时期,以目前评估的每股净资产价格购买一定数量的公司股份。届时如果每股净资产已经升值,则股份期权持有人获得潜在的收益,反之,以风险抵押金补入差价。因而,对于未定权益获得者(如公司管理人员)来说,如何对即将获得的权益进行保值是一个极为现实的问题。
关于未定权益的套期保值,在市场完备的情况下,可以利用其相关的资产,通过自融资方式而进行完全复制;但是,在市场不完备的情况下,对于一般未定权益而言,无论采取何种自融资方式都不能完全对冲未定权益可能面临的风险。如何最大程度地降低风险则成为投资者所要考虑的问题。许多套期保值标准也被相应提出,平方标准就是其中之一。NICOLAS等[1]提出均方准则,即把终期财富与未定权益之差的平方的期望E(VT-H)2作为风险。很多学者在此准则下进行了套期保值研究。CERNY[2]运用动态规划原理研究了离散时间下的平方对冲,并得到最优策略的递归方程形式解;DUFFIE等[3-4]研究了扩散模型下的平方套期保值,并得到最优策略的显式解。余星等[5]基于效用函数理论,通过构建等价鞅测度,证明在风险厌恶一般效应函数下,考虑计划成本的最优期货期权套期保值模型最优解的存在性和唯一性,并得出负指数效用函数下的最优套期保值显式解。
不同投资者对市场风险存在的认同感和对风险的偏好程度并不一致。黄金波等[6]研究发现,不同风险厌恶程度投资者有不同的风险对冲策略偏好。赵树然等[7]综合考虑收益、风险和反映套期保值者态度的CVaR为优化目标,结合ECM-DCC模型,构建动态CVaR套期保值模型,得出期货最优套期保值比,但没有进一步分析套期保值者的风险态度对套期保值效果的影响。
纵观现有的研究,很少区别套期保值主体的个性差异,得出的套期保值策略也没有考虑投资者对风险的偏好差异。鉴于此,本文在不考虑交易费用及完全市场条件下,首先,把效用函数与风险厌恶系数相结合,构建不同风险偏好投资者的风险规避目标函数;然后,借助动态规划方法,提出随机支付型未定权益套期保值策略的构造方法,计算不同时刻的最优套期保值比。
2 效用函数与套期保值模型
2.1 效用函数
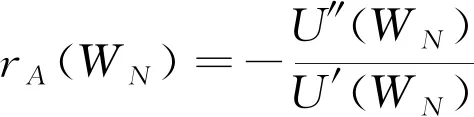
本文主要分析两种与风险相关的效用函数:
2.2 套期保值模型
假设套期保值者在初始时刻获得一份将在T时刻支付的未定权益(如公司管理层的奖励),为了使期末获得的权益资产效益最大,确定在[0,T]期内,以Δt=T/N为时间间隔的离散时间集t∈{0,Δt,2Δt,…,NΔt}上利用与未定权益相关的另一种资产(如以公司股票为标的资产的期货合约)进行套期保值操作。
设St表示未定权益在t=nΔt时刻的价格;Ft表示期货合约在t时刻的价格;ϑt表示套期保值过程中在t时刻持有期货合约的空头头寸;Wt表示t时刻进行套期保值头寸调整前拥有的资产价值;W0表示初始时刻拥有的资产价值;r表示固定的无风险收益率。则套期保值者在各时刻拥有的资产价值可表示为
(1)
其中,R=exp(rΔt)。
以期末资产效用最大为目标,并且以式(1)为自融资约束,可以建立如下套期保值模型:
(2)
其中,E1[U(WN)]是期望效用函数,表示期末财富的期望效用,而且Et[·]=E[·|Ft];t=1,…,N表示在t时刻的信息条件下对应的条件期望,类似地,后文的Vart[·]=Var[·|Ft],t=1,…,N表示条件方差。
3 最优套期保值比的确定
3.1 基本原理
根据贝尔曼最优性原理[14],套期保值问题(2)可以表示为

(3)
因而,对于优化问题(3),可以从N-1时刻开始,采用倒向递推方法,求出各时刻的最优套期保值比。
3.2 最优套期保值比

(4)
证明根据动态规划原理,可以采用倒向递归方法对定理证明。
①当t=N-1时,根据式(1),可得:
WN=RWN-1-(FN-FN-1)ϑN-1+SN
(5)

(6)
对式(6)关于ϑN-1求导数,并令等于0,可得:
(7)
在市场无套利的情况下,期货价格加期货交易成本(如交易手续费等)等于现货价格加现货交易成本(如保管费用、借入资金的利息成本等)[15]。如果不考虑交易成本,即有EN-1(FN)=FN-1。随期货合约到期日的临近,期货与现货期末基差趋于零,即有FN=SN,因此,式(7)进一步简化为
(8)
参照文献[16],当t=N-2时,把式(8)代入WN=RWN-1-(FN-1-FN-2)ϑN-1+SN,并根据式(1),有:

(9)

(10)
对式(10)关于ϑN-2求导数,有:

(11)
令式(11)等于0,可得:
(12)
与t=N-1类似,在市场无套利、并不考虑交易费用的情况下,EN-2(FN-1)=FN-2,同时,因为期货与现货期末基差趋于零,即有FN=SN,则式(12)可表示为
(13)


事实上,当t=n时,由式(1)可得资产价值递推表达式:

(14)


(15)
在市场无套利和期末基差为零的情况下,解如下优化问题(16):

(16)
对式(16)关于ϑn求导数,有
(17)
在市场无套利、并不考虑交易费用的情况下,有En(Fn+1)=Fn,同时,因为期末基差趋于零,即有FN=SN,故令式(17)等于零,可得t=n时刻的最优策略:

(18)
证毕。
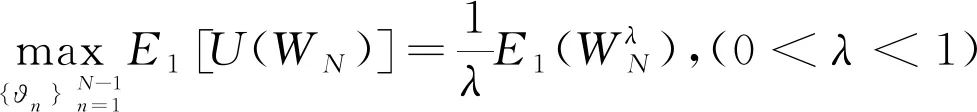
(19)
证明
然后,用类似定理1的方法,证明定理2的结论。


(20)
对式(20)两边取期望,并代入WN=RWN-1-(FN-1-FN-2)ϑN-1+SN,有:

(21)
对式(21)关于ϑN-1求导数,有:

(22)
在市场无套利、并不考虑交易费用的情况下,有EN-1(FN)=FN-1,同时,因为期末基差趋于零,即有FN=SN,把EN-1(FN)=FN-1和FN=SN代入式(22),并令式(22)等于零,可得
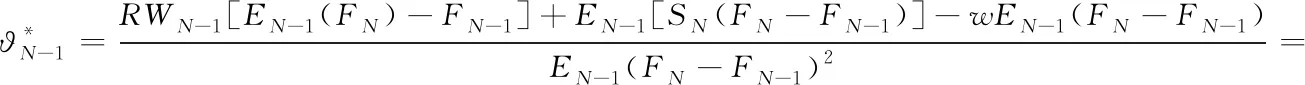
(23)
当t=N-2时,把式(23)代入WN=RWN-1-(FN-1-FN-2)ϑN-1+SN,并根据式(1),有:

(24)


(25)
把式(24)代入式(25),关于ϑN-2求导数,

(26)
在市场无套利,即EN-2(FN-1)=FN-2及期末基差为零,即FN=SN的情况下,令式(26)等于零,可得:
(27)


由式(1)可得资产价值递归表达式:

(28)

(29)
(30)

证毕。
4 结论
本文主要基于效用理论,研究了未定权益的最优套期保值策略问题。首先,把效用函数与风险厌恶系数相结合,构建不同风险偏好者的风险规避目标函数;然后,借助动态规划原理,提出未定权益套期保值策略的构造方法,计算不同时刻的最优套期保值比;最后,证明了在市场无套利情况下,以均方效用和幂效用目标下的最优套期保值比与风险规避系数无关,两者有相同的最优策略。

