基于三维设计主成分分析的电网工程算量信息权重提取方法
孙安黎 向 春 喻建波
(重庆电力设计院有限责任公司 重庆 401120)
0 引 言
三维设计主成分分析(Principal Component Analysis,3DPCA)通常使用于模式识别、特征提取等方面的一种统计学理论方法。该方法能够有效、精准地提取出所需的主成分,去除非主成分[1]。电网工程算量信息包括对象化工程和非对象化工程计算的相关信息。由于电网工程算量包含的种类较多,且每个种类对应多个单项指标,指标之间又存在或多或少的关联性,主要信息和非主要信息混杂在一起,使信息提取变得很困难。为了更好地管理电网工程的算量信息,如何确定几个重要单项状态量的权重显得尤其重要[2]。
目前针对电网工程算量信息权重提取方法的研究有很多,例如:徐长宝等[3]研究的基于贝叶斯理论的继电保护设备状态评价权重更新方法,该方法依据继电保护设备的各状态指标,利用贝叶斯理论的先验概率思想进一步提取、融合继电保护设备实际运行数据特征得到权重的分布,但是该方法在获取权重分布时的召回率略低;白恒远等[4]研究基于拉格朗日函数的配电网评价指标权重,该方法利用拉格朗日函数的经济学意义来确定指标权重,但是该方法确定的权重并非是原始指标的权重,而是经过分析之后的各个成分的权重,无法直接加以利用。因此,为了提高电网工程算量信息权重提取的效率,提出基于三维设计主成分分析算法的电网工程算量信息权重提取方法,更好地管理电网工程算量信息。
1 电网工程算量信息权重提取
1.1 基于3DPCA的电网工程算量信息采集
为了实现三维设计的空间中的电网工程算量信息权重的采集,需要确定三维设计空间内的电网工程算量信息的内容[5]。
设定3DPCA的协方差三维矩阵为:
(1)
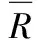
1) 高维张量二维矩阵展开方式:以N=3为例,设置H∈Rb1×b2×…×bN的N维张量可开展为H1、H2、H3的三种二维矩阵。H的奇异值分解为:
(2)
式中:W是H的奇异值三维矩阵;×N为N模式乘法;D(N)是对应H的N模式的酉矩阵。
通过高阶张量展开式(2)后得出:
H(N)=D(N)·W(N)·(D(N+1)⊗D(N+2)…D(N)⊗
D(1)⊗D(2)…D(N-1))T
(3)
式中:⊗为Kronecker乘积;T为阶数。
式(3)能够转换为下述三种方式:
(4)
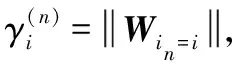

(5)
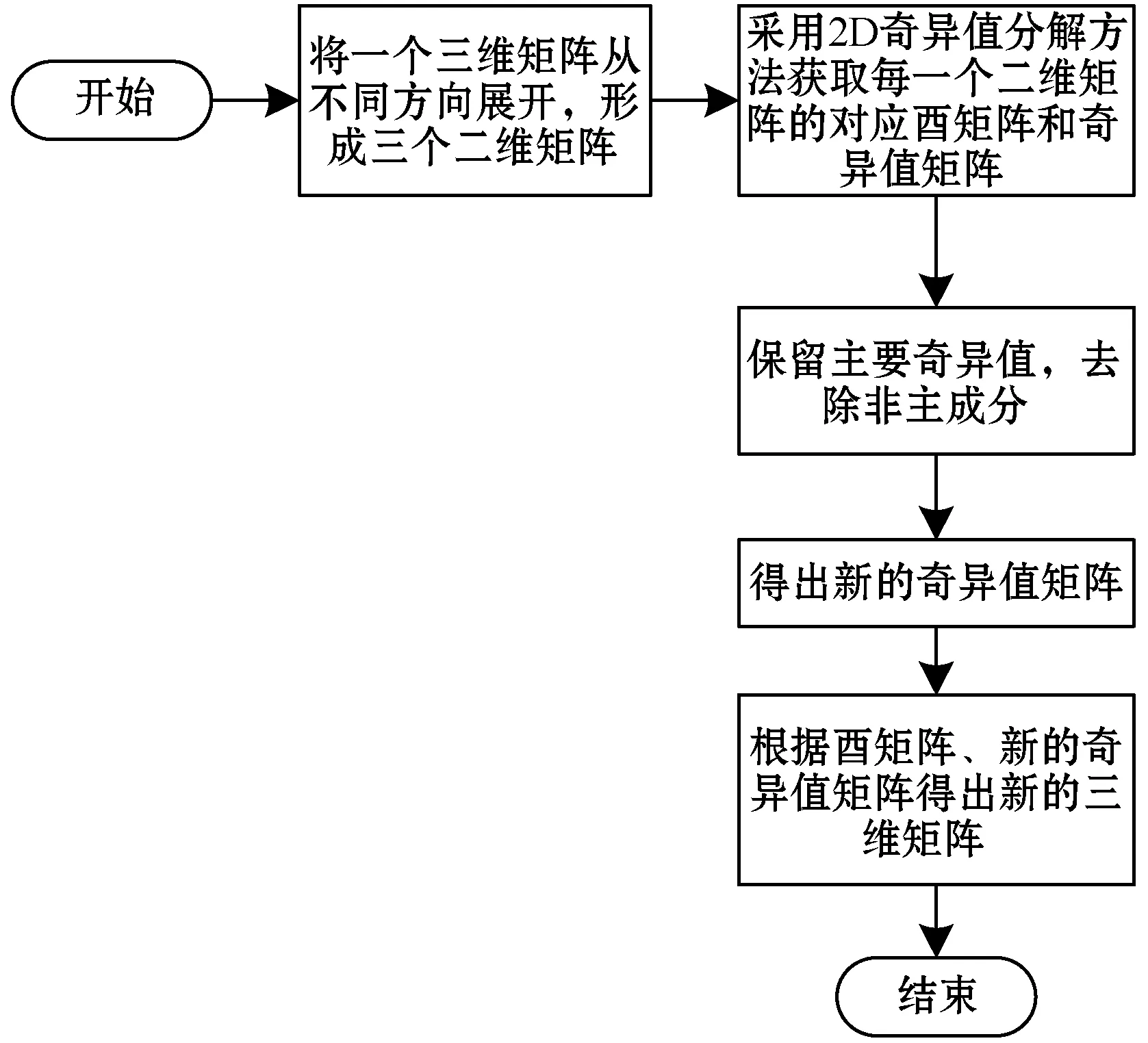
图1 3DPCA算法流程
通过采集的电网工程算量信息,可进一步建立评判矩阵,以提取电网工程算量信息权重。
1.2 评判矩阵建立
评判矩阵是电网工程算量信息权重提取的基础,提取电网工程算量信息权重信息量,需要确定其重要指数的单项算量信息指标数量h,通过对电网工程算量具有丰富经验的Q位专家人员(ZJ),得出h组算量信息Sh专家评分值Pi,j,i=1,2,…,Q;j=1,2,…,Q,其中每组数据中具备Q个元素,以此得出专家人员打分评判如表1所示。

表1 专家人员评分表
由于各专家人员所在的岗位和研究方向不同,导致评分结果存在误差。但是经过研究发现,咨询的专家人数越多,最终获取的工程算量信息权重指数就越科学。因此,为保证所提取到的电网工程算量信息权重的精准性,通过各专家人员给出的指标评分之间的线性关系,简化指标评分[8-9]。通过主成分分析法获取电网工程算量信息权重。
1.3 电网工程算量信息权重获取
电网工程算量信息权重获取的过程就是利用主成分分析法,以提取到的电网工程算量信息内容为基础,结合评判矩阵,获取综合评价函数的过程[10]。其核心是从新的三维矩阵中的获取的电网工程算量信息的内容后,选择几种主成分指标,使这些主成分指标,尽量具有完整的原来指标的信息,并且指标之间没有关联[11]。保证主要工程算量信息不丢失的情况下,解决了指标间的共线性,其基本原理是:通过一个正交变换,将与指标相关的原始随机变量X=(x1,x2,…,xp)T转换成与其不相关的新的随机多维变量C=(c1,c2,…,cp)T,并指向已选指标样本点分布最大的p个方向,对多维变量U完成降维处理,使其转换成一个精度很高的低维变量[12]。主成分分析算法计算电网工程算量信息权重,可以看作是通过因子载荷矩阵获取原始指标变量的线性组合,将因子载荷矩阵中的每列系数矩阵与其相应特征值的平方根相除,得出指标在主成分中的比重,将每个主成分所对应的特征值,占所提取主成分总的特征值之和的比例,作为权重计算主成分综合模型[12-15]。综合模型中的比重,经归一化处理得到因子在综合模型中的权重。
权重模型就是主成分模型,其为:
(6)
式中:分析后取得的m个主成分和决策矩阵中的系数分别为K1,K2,…,Km和cQj,各指标i的权重指数为φi,(i=1,2,…,Q)。由于在主成分分析时,获取的结果是一个初始因子载荷kQj,并不是决策矩阵中的系数,因此两者之间的换算公式为:
(7)
式中:ξj为主成分特征值,j=1,2,…,m。
根据式(6)和式(7),建立综合评价函数KZ为:
(8)
κ=ξ1+ξ2+…+ξm
(9)
式中:φ1,φ2,…,φQ为指标o1,o2,…,oQ在主成分中的综合重要度;κ为所有主成分特征值之和。
结合式(9)和专家评分值,获取原指标的综合值SZi为:
(10)
根据式(9)获取各指标权重指数为:
(11)
结合式(8)-式(11)获取二级权重模型为:
(12)
综上,通过高阶张量奇异值分解方法保留主成分,根据新形成的三维矩阵,提取权重的信息的初始位置,获取完整的电网工程算量的信息内容;依据电网工程算量的信息内容获取电网工程算量信息主成分指标,通过建立权重模型获取主成分特征值和初始因子载荷,完成各指标权重指数提取。
2 测试结果分析
以某电网公司的工程算量中的对象化工程算量和非对象化工程算量两大种类指标为测试对象。选取对象化工程算量中的5个相关单项指标为:电缆沟、检查井、端子箱、线路塔杆和框架柱。选取的非对象化工程算量中的5个相关单项指标为:排水、电气照明、零星砌体、地基处理和场地平整。采用本文方法提取该电网工程算量信息权重,并通过对比方法验证本文方法优势。
2.1 工程算量信息权重提取
邀请5位专家人员根据单项指标算量信息和综合算量信息之间的关联度,完成单项指标算量评分,获取评价得分表如表2所示。
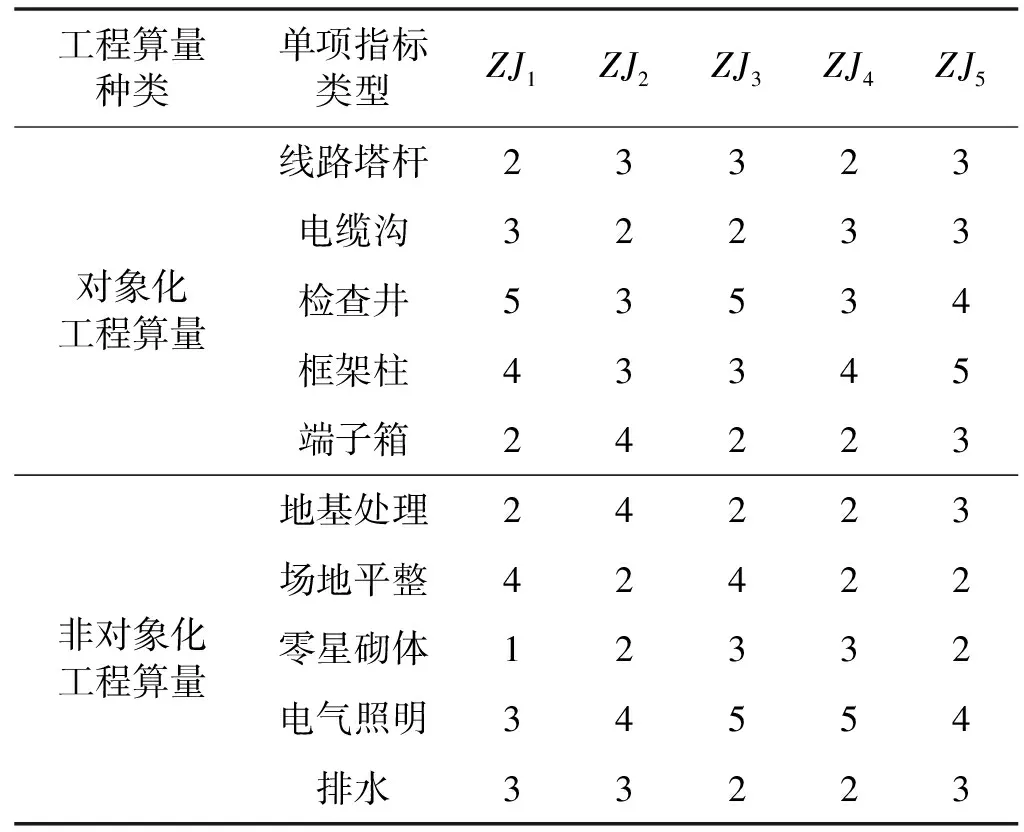
表2 单项指标算量信息专家评分表(分)
表2中,1分为不重要;2分为不太重要;3分为一般重要;4分为比较重要;5分为非常重要。
将表2中的单项指标原状态算量信息,进行主成分分析,获取主成分单项指标初始因子载荷和成分特征值,分别如表3和表4所示。

表3 主成分单项指标初始因子载荷
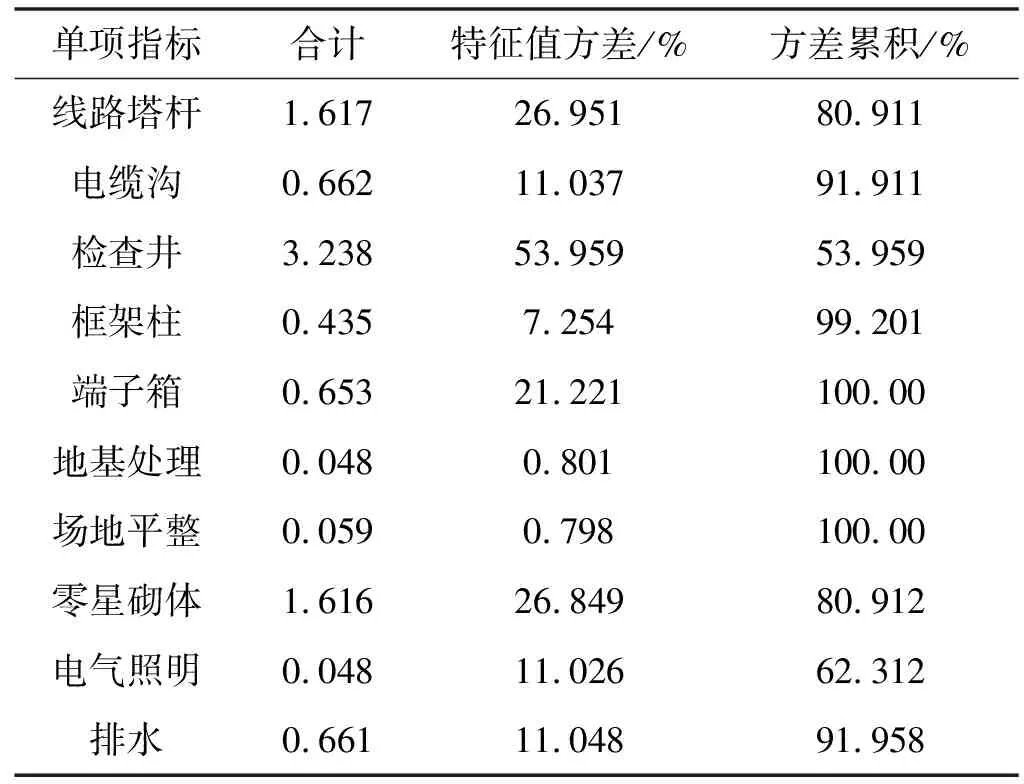
表4 成分特征值
主成分数量提取原则是对应主成分特征值大于1,并且主成分贡献率≥85%的前m个主成分。分析表3数据可知,该电网公司的工程算量中的对象化工程算量和非对象化工程算量均有两个主成分,对于对象化工程算量而言,电缆沟、框架柱两项单项指标在主成分2上的载荷较高,说明主成分2可以显著体现电缆沟、框架柱的信息;线路塔杆、检查井和端子箱等单项指标在主成分2上的载荷较高,说明主成分1主要体现这三种信息。同理可知在非对象化工程算量中,主成分1主要体现地基处理、场地平整、零星砌体和电气照明4项信息,主成分2主要体现排水信息。综上可知,主成分1和主成分2基本可以体现该电网工程算量的全部信息。
利用式(7)计算表4中的结果,可以得出cQj;结合表2、表4及式(6)得出的结果,一同代入式(12)中,得出对象化和非对象化工程算量中各单项指标算量信息的权重指数依照表4中的排列顺序由上到下依次为0.115、0.1306、0.205、0.191、0.145 9、0.211、0.145 8、0.115 8、0.210 5和0.130 7。
2.2 性能测试
2.2.1召回率测试
为验证本文方法的提取性能,采用基于贝叶斯理论的继电保护设备状态评价权重更新方法(文献[3]方法)和基于拉格朗日函数的配电网评价指标权重提取方法(文献[4]方法)与本文方法作对比,选取召回率和F1-measure均值作为方法的测试指标。召回率越大表明提取结果越精准;F1-measure均值越大,提取效果越好。随机选取对象化工程算量中的端子箱单项指标进行10次提取测试,测试结果如图2和图3所示。
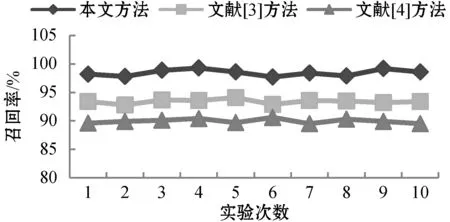
图2 三种方法的召回率对比结果
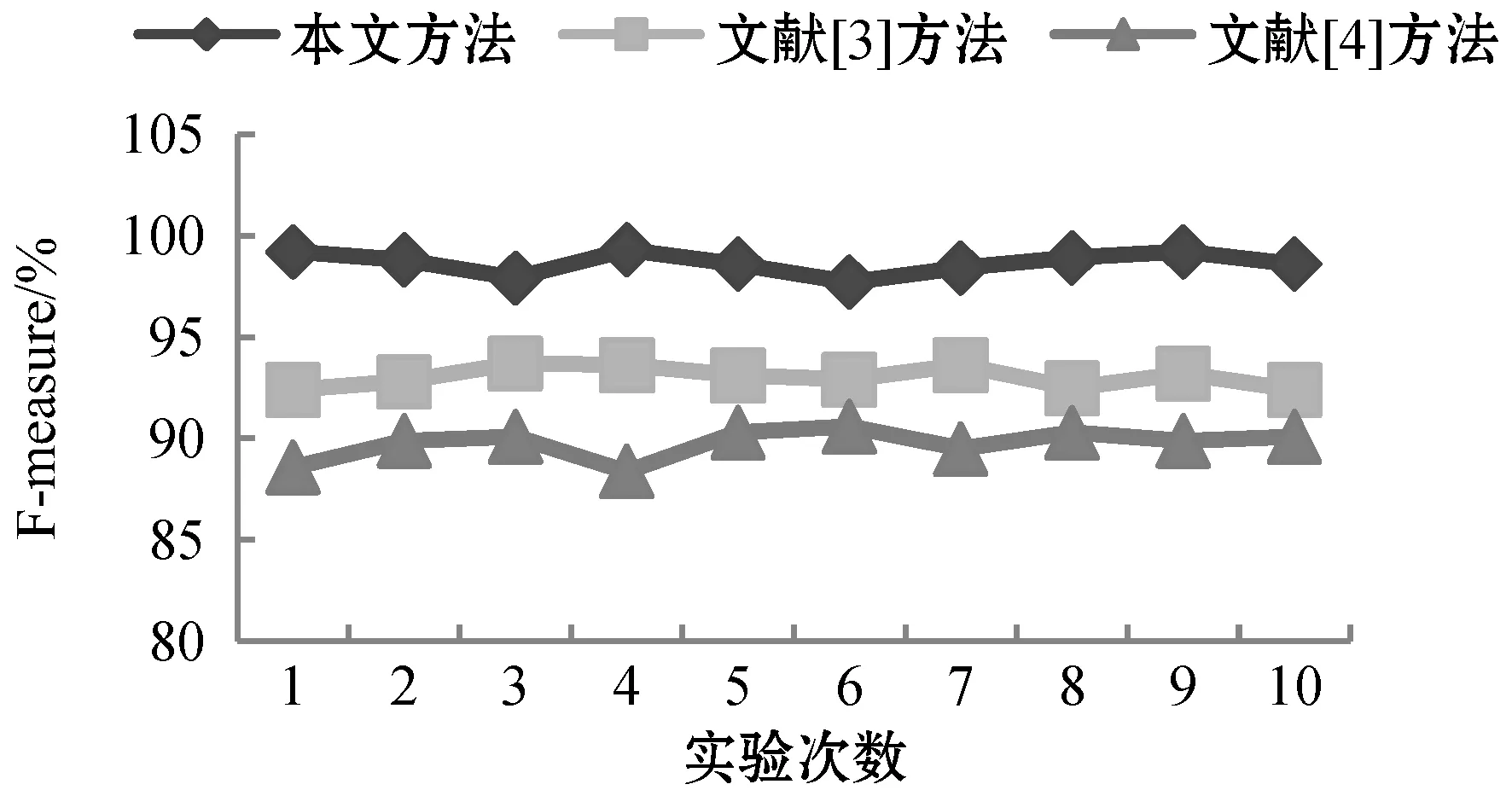
图3 三种方法的F-measure均值对比结果
分析图2图3可以得出:本文方法的召回率和F1-measure均值分别为97.5%、97.0%左右,文献[3]方法的召回率和F-measure均值分别为94%和93%左右,文献[3]方法的召回率和F-measure均值分别为90%和89.6%左右,说明本文方法信息提取的查全性较好,具备明显优势。实验结果表明本文方法的电网工程算量信息提取效果好,原因在于本文方法在信息提取时,去除了影响工程算量信息提取的冗余信息,获取完整的电网工程算量的信息内容,使信息提取效果更好。
2.2.2准确率测试
为了验证本文方法对电网工程算量信息权重提取的准确性,测试三种方法在没有噪声和有噪声的情况下,对象化工程算量的5项指标的信息权重提取的准确率,测试结果如表5所示。

表5 五项指标信息权重提取准确率对比结果(%)
通过观察表5可以看出:本文方法在没有噪声和有噪声的情况下,提取不同的单项指标信息权重准确率均在98.5%以上,另外两种对比方法在没有噪声的和有噪声的情况下,准确率均在94%以下,且存在较大浮动。说明本文方法具备较高的电网工程算量信息权重提取准确率,且几乎不受噪声影响。
2.2.3效率测试
为了测试本文方法的提取效率,测试三种方法在15 s内,提取大小不同的对象化工程算量信息权重时的提取效率,对比结果如图4所示。
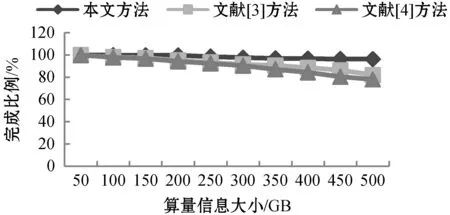
图4 三种方法提取效率对比结果
分析图4可以看出:在相同的15 s的时间内,针对不同大小的算量,信息权重提取效率均在96%以上,即便信息大小为500 GB时,本文方法在15 s内依旧完成96.4%的算量信息权重提取;另外两种对比方法,随着算量信息大小的增加,提取效率明显下降,当信息大小为500 GB时,分别完成了82.1%和78.2%的算量信息权重提取,明显低于本文方法的提取效率。说明本文方法的提取效率较高,能够快速地完成工程算量信息权重提取。
综上所述,本文方法的召回率和F1-measure均值分别为97.5%、97.0%左右,在没有噪声和有噪声的情况下,提取不同的单项指标信息权重准确率均在98.5%以上,在相同的15 s的时间内,针对不同大小的算量,信息权重提取效率均在96%以上,即便信息大小为500 GB时,本文方法在15 s内依旧完成96.4%的算量信息权重提取。主要原因在于本文方法引入三维设计主成分分析,得出要提取权重的信息的初始位置,并采用区域生长法,获取完整的电网工程算量的信息内容,更好地管理电网工程的算量信息。
3 结 语
本文研究了基于三维设计主成分分析算法的电网工程算量信息权重提取方法,三维设计主成分分析算法能够有效、精准地提取出所需的主成分,去除非主成分特点获取电网工程算量信息内容,基于此信息内容,采用主成分分析法的权重指数确定方法,建立了权重计算模型,实现电网工程算量信息权重提取。然而,针对基于三维设计主成分分析算法的电网工程算量信息权重提取,还需不断进行拓展研究,例如实现变电工程的量价联合计算、自动计算、如何运用到输变电工程甚至电网工程全面造价管理等问题,以及如何基于三维设计主成分分析,实现数字化的电网工程管理。

