高空气球发放过程中的流固耦合动力学研究

苏 一,张向强,刘 强

(1. 中国科学院空天信息创新研究院,北京 100094;2. 中国科学院大学,北京 100049)

1 引言

临近空间(Near Space)通常被定义为距离地面18-100km高度的高空区域,其位于地球大气中的平流层和中层,是一个待开拓的具有重要战略意义的空间圈层。在这一空间圈层的中低层(18-50km)运用最为广泛的平台是高空气球,高空气球根据球膜是否承受内外压差通常被划分为零压气球和超压气球,从上世纪五六十年代开始,零压气球由于其成本低、载重大、发放简易等优势,在空间科学领域方面发挥了重要的作用[5-7];1997年,NASA提出了ULDB计划,其目的是完成超压气球载重1.6吨、驻空33.5km,续航100天的飞行任务,目前已实现驻空54天的飞行[8]。由于临近空间的大气密度较小,海拔20km的大气密度是地面的1/14,海拔35km的大气密度是地面的1/150,即为维持浮力重力平衡,高空气球的体积很大,同时材料面密度要小或厚度薄。目前国内外常用的球膜材料一般为聚乙烯,体积达几万至几十万立方米,球膜厚度在20～80微米之间。若设计升限为40～50km,材料的厚度降为几微米左右[13]。因此,基于气球的形变和应力分析的球形设计始终是高空气球的难点[14]。

高空气球发放方式大体上可分为静态发放、半动态发放和动态发放[2-4],不管采用哪种发放方式,解除约束后气球受力和形态变化剧烈,典型的气球发放过程如图1所示。

图1 高空气球发放过程

2 发放过程系缆分析

2.1 数学模型

假设气泡(球体充气部分)刚性,结缆系统和气泡以下的球体部分视为柔性系缆,简化后的模型受力如下图所示。

考虑在X,Y坐标下气球某位置上球体微段的受力,它包括张力T和T′=T-dT,重量dW.g,风对该线段的阻力dDr,在瞬时位置要求每一个微段受力平衡,在系缆没有触地的时候满足以下平衡方程[1]:

X方向有,

T·cosθ+dDr·cosα=(T-dT)·cos(θ-dθ)

(1)

Y方向有,

T·sinθ=dW·g+dDr·sinα+(T-dT)·sin(θ-dθ)

(2)

化简得,

dT=dDr·cosα·cosθ+(dW·g+dDr·sinα)·sinθ

(3)

另外有

dx=cosθ·dl

dy=sinθ·dl

(4)

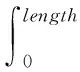
(5)

ODE45是一种自适应步长的采用Runge-Kutta算法常微分方程数值解法,给定微分方程、积分范围和参数初值可以得到积分范围内的解析解。积分的初始值为[T0θ0X0Y0],X0=0,Y0由高空气球所处的位置决定。通过打靶法,并以二分法优化初值的搜索过程,初值T0和θ0建立以下的关联

T0=F·sinθ0

(6)

其中,F为高空气球产生的净浮力,这样T0的初始值由θ0决定,初始值变为[F·sinθ0θ0X0Y0],变量只有一个,确定θ0的取值范围,通过打靶法找到确定的θ0,就可以完成曲线的拟合。

假设有

dDr=fDr·dl

dW=ρ·dl

(7)

其中fDr系缆单位长度所受风阻,ρ为线密度,根据(7)化简(3),这样积分时以dl为自变量,积分区间为系缆长度,根据公式,并考虑初值的正负性,则ODE45初值公式为

=-fDr·cosα·cosθ+(ρ·g-fDr·sinα)·sinθ

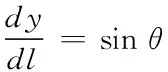
(8)

其中α和θ之间有

(9)

当系缆触地后每一个微段会有

T′+Ff=T

(10)

Ff=f·FN

(11)

根据图2可知,触地后系缆微段的微分方程为

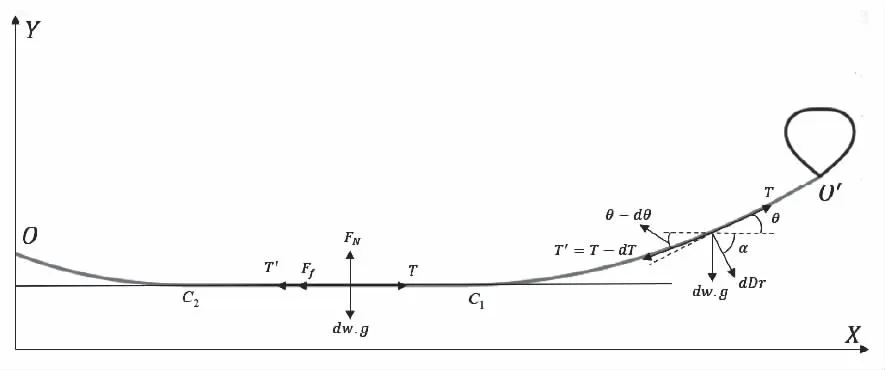
图2 系缆受力图

(12)

确定系缆的曲线后,考虑系缆是否触地,将曲线做出后和地面的高度比较,判断系缆曲线是否与地面直线相交,若不相交,则系缆曲线为所求;若相交,则分段打靶求曲线。第一段打靶根据初始条件找出满足与地面相切的点C1,相切条件为目标点C1(y=0,θ=0),然后根据触地后的微分方程,根据区间设定点C2的范围为(C2,O),作为第三段打靶的初始条件,打靶最后收敛于目标点O,反过来确定C2的位置。

高空气球在发放过程中会受到来自空气的阻力

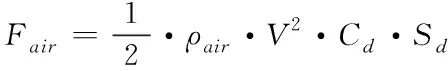
(13)

其中,Fair为空气阻力,ρair为空气密度,V为高空气球体积,Cd空气阻力系数,Sd为高空气球受力面积。由上文可知,每次可以通过确定的位置得到当时球体的受力情况,如图3所示,确定系缆的曲线初值为[F·sinθ0θ0X0Y0],而只需要给定Y0就可以通过打靶法确定曲线,故只需分析Y方向的受力情况,根据基本的运动学公式

图3 高空气球受力图

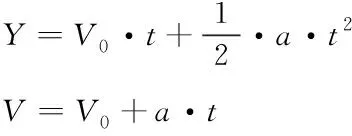
(14)

Y方向受力情况为

F=T·sinθ+Fair+(MHe+Mballoon)·a

(15)

本次数学模型采用VBalloon=7m3的小型高空气球,充入30%的氦气作为浮升气体,经过

FHe=ρair·VHe·g

GHe=ρHe·VHe·g

(16)

F=FHe-GHe-MBalloon·g

(17)

其中,VHe=0.3·VBalloon,经过计算可知F=22.12N,因为充气量存在误差并且球膜的质量不可控,经测量净浮力为21.52N。

通过MATLAB中ODE45函数求解后,高空气球在高度Y方向的加速度、速度、位移和系缆末端O′点拉力随时间的变化如图4所示。

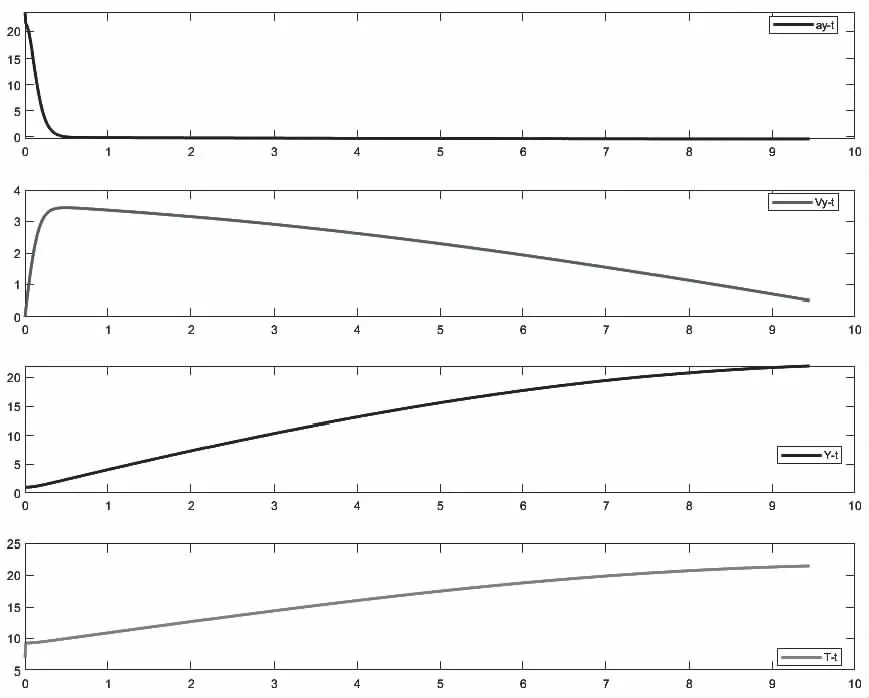
图4 高空气球运动曲线

由高空气球运动轨迹可知,气球在初始时加速度较大,速度在到达峰值后逐渐变小。

2.2 有限元仿真

通过MATLAB中的计算结果可知,在初始时刻发放车和高空球底部的直线距离为20.76m,在DYNA的前处理中将系缆未与高空气球相连的一端通过添加初始位移的方法将距离调至相同,并通过添加重力达到发放的初始状态的参数设置相同距离,除此之外,高空气球高度、发放车高度、系缆的粗细、长度和线密度以及系缆所受的重力和高空气球产生的浮力均与数学模型一致,在LS-DYNA中建立模型如图5所示。

图5 高空气球系缆随时间变化(间隔1s)

图6 LS-DYNA模型初始状态

图7 LS-DYNA仿真系缆形状变化(间隔1s)

高空气球在上升中受浮力和重力相互影响,在LS-DYNA中取全局阻尼为3.5,计算结果如图8～11所示。

图8 气球加速度随时间变化

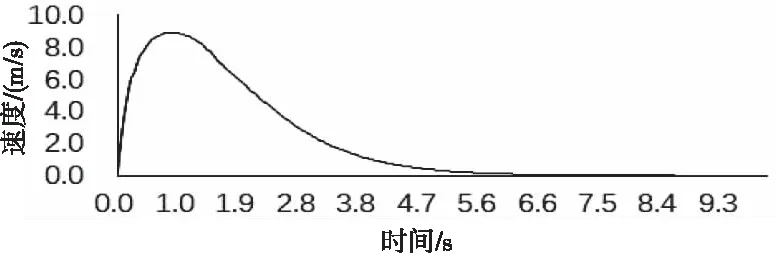
图9 气球速度随时间变化

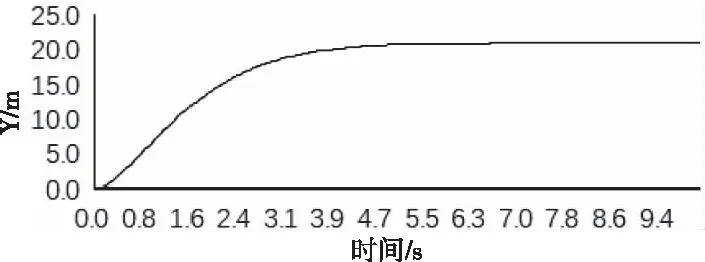
图10 气球高度随时间变化

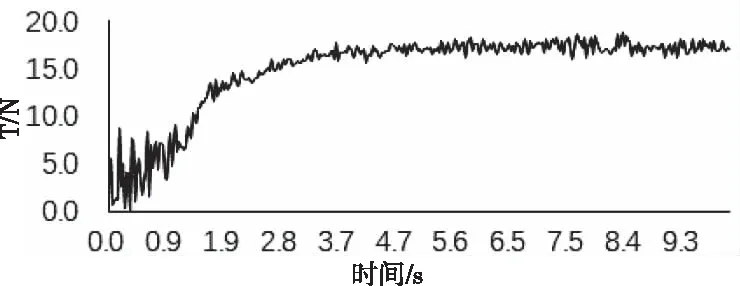
图11 系缆拉力随时间变化

图12 高空气球受力分析

图13 高空气球初始形状

通过LS-DYNA仿真可以看出,MATLAB和LS-DYNA计算结果说明高空气球在发放过程中确实会受到系缆拉力作用,但LS-DYNA中无法做到根据用户要求定义阻尼大小,故速度峰值会有所不同。

3 发放仿真

在LS-DYNA中进行动力学仿真,观察球膜的形状以及应力变化,因此球膜需要转化成柔性体,通过在球膜里面加入SPH粒子来模拟氦气,通过SPH和球膜的相互作用,对发生冲击时球膜和气体进行耦合分析。

3.1 高空气球球型模型

气球球膜一般由厚度为20μm左右的薄膜制成,球膜的厚度和球体尺度相比很小,符合无矩薄壳理论使用的条件[12]。

由回转薄壳无力矩理论可知:

(18)

其中

(19)

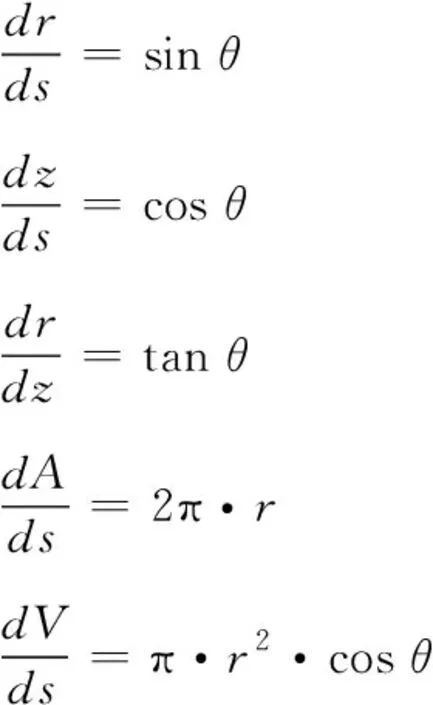
(20)

将式(19)(20)代入(18),并化简得

(21)

在截面圆上的总负载T=2πrσm在弧长方向的改变程度和周向应力在弧长方向的分力以及膜重的和应保持平衡,如式(22)所示。

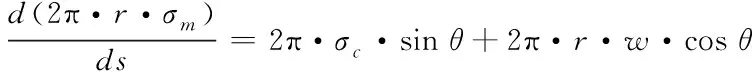
(22)

化简式(22)得

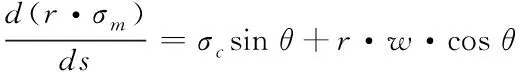
(23)

球形参数λ和∑的定义如式(24)所示,λ和Σ表示了气球负载L及飞行高度对球形的影响程度

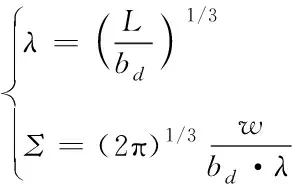
(24)

自然形高空气球应当保证周向应力σc=0,上式共同组成球形母线的求解微分方程组,在NASA高空气球手册中有Σ表,不同的Σ值对应不同的母线形状,本文采用的Σ=0.3,成型后的形状图14所示。

图14 高空气球柔性球膜发放过程

3.2 SPH方法

SPH方法(Smoothed Particle Hydrodynamics)全称为光滑粒子流体动力学方法[10],是一种为求解流体的动力学问题而提出的一种无网格方法。一般流体动力学问题需要基于密度、速度、能量等变量场的偏微分方程组,而SPH方法是通过采用插值方法将连续的流体用相互作用的质点组来描述,每个质点上包含各种物理量的信息,这样再过连续介质力学的守恒定律可以将整个流体过程描述出来,从这个方面来说,只要采用的质点粒子数够多,就能准确的描述流体的力学行为。

在有限元计算中,SPH是一种纯Lagrange方法,SPH由于不存在网格关系,所以不存在由于变形过大导致的网格畸变问题,因此适合求解高速碰撞过程中的大变形问题。

3.3 接触算法

LS-dyna在处理接触问题的过程中主要采用以下三种不同的算法:

1)动力约束法

2)分配参数法

3)对称罚函数法。

LS-DYNA的一般默认采用对称罚函数法,是计算中最常用的一种方法。

其首先要确定接触面的主从关系,一般从接触面比主接触面的网格更密,然后在计算过程中的每一个时间步都判断从节点是否会穿透主表面,没穿透则不操作;若穿透,则对从节点和接触面之间引入一种限制穿透作用的类似法向弹簧的接触力,接触力的大小和穿透深度、接触刚度有关,具体如式(25)所示

F=K·δ

(25)

其中,K为接触界面刚度,δ为穿透量。这种接触算法应用简单,不需要添加碰撞和释放条件,而且计算过程中保持动量守恒。在球膜与氦气耦合过程中,氦气为从节点,球膜为主接触面[9]。

3.4 冲击仿真

3.4.1 材料参数

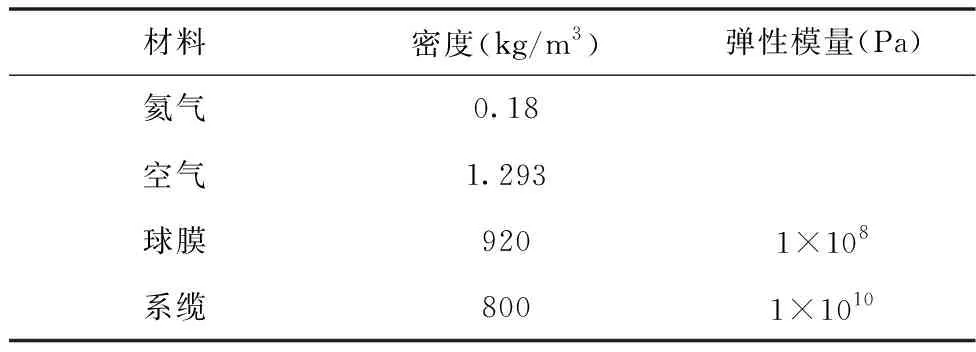
表1 仿真参数表

3.4.2 高空气球发放冲击模拟

本文研究的高空气球的发放过程是高空气球在充气完毕后在滚筒的约束下保持稳定为发放零时刻,之后打开发放滚筒到气球升起并在升到系缆的极限长度后在下方发放车的约束下停止并保持稳定的一个过程。

3.4.2.1 建立模型

首先根据Σ=0.3做出球型的母线,将母线导入UG建立模型,再用ICEM为模型画网格,用LS-prepost进行前处理,并加入SPH粒子,建立好的网格模型如下图所示。其中高空气球体积为7m3,冲入的氦气为气球体积的30%,然后对氦气施加浮力,对球膜和系缆施加重力,获得初始稳定的形状。

利用文章2.2章节中所采用的仿真方法,如图5所示,将球膜转换成柔性体并冲入30%氦气,会得到如图15所示的球膜以及系缆曲线。

图15 高空气球充氦气后形状与实际对比图

发放过程中会出现冲击是在系缆拉直,球膜会向系缆方向收紧,和竖直向上所受冲击模式类似,故可以采用竖直向上发放的方式研究受到系缆和气体冲击时球膜所受应力变化。

3.4.2.2 添加场力

因为建立的模型外部并没有气体,所以要让氦气产生向上的浮力气体的密度并非氦气的密度,而是通过浮力公式进行换算,算出的密度应当将外部气体和氦气的密度都考虑进去,根据式(16),有

F净浮力=FHe-GHe=ρair·VHe·g-ρHe·VHe·g

=ρHe′·VHe·g

(26)

故有

ρHe′=ρair-ρHe

(27)

这样,预先充入的气体在受到向上的加速度g时,可以产生向上的且符合实际的浮力,球膜和系缆通过关键字*LOAD＿GRAVITY＿PART施加重力,获得初始形状如图16所示。

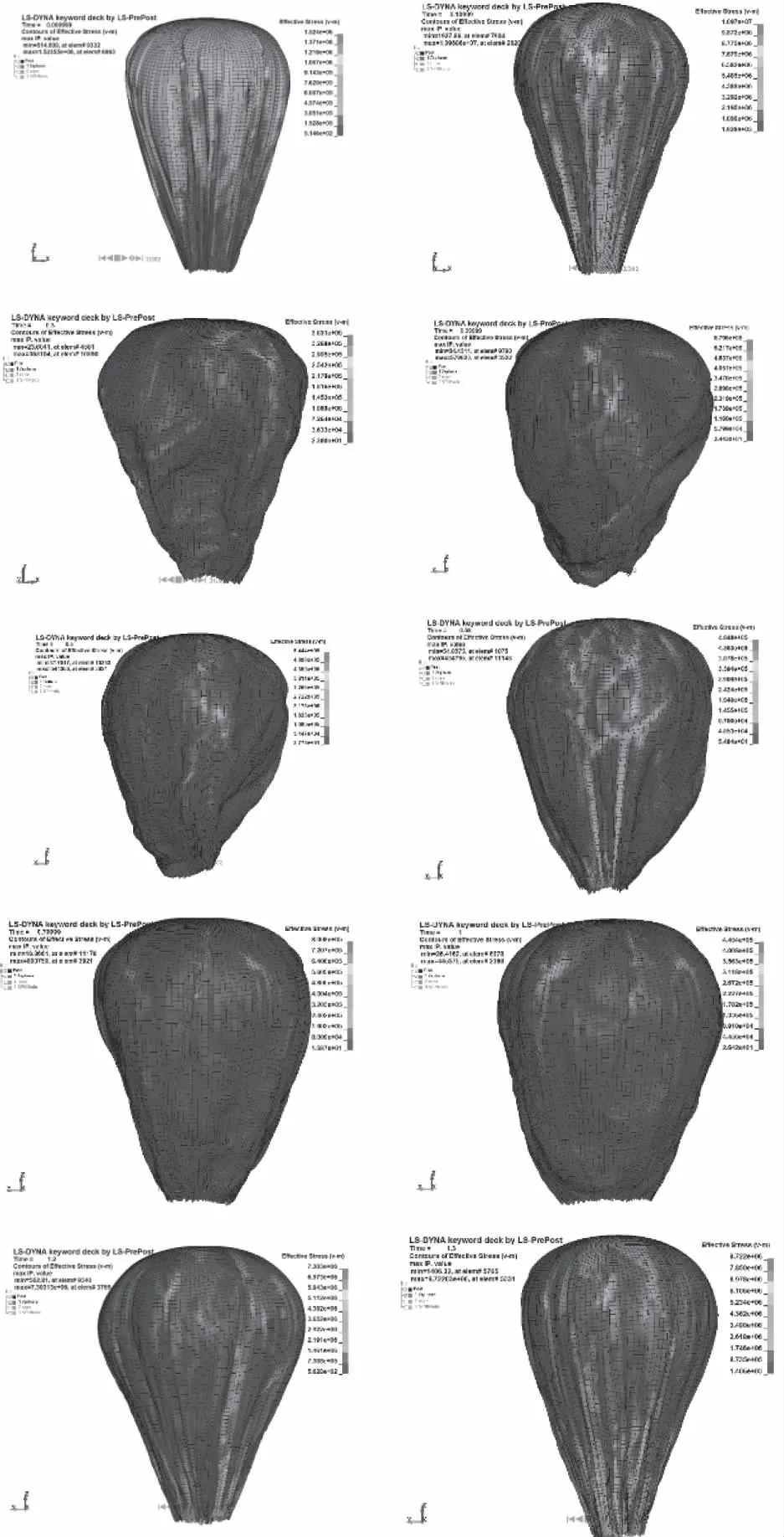
图16 高空气球冲击受力图

高空气球成型后的形状是内部流场和外部流场对球膜共同作用的结果,由于仿真后的高空气球模型没有加入外部流场,故来自于外部流场的压强和风场并没有作用在球膜上,图15中球膜的形状是在内部流场作用下稳定的结果。

3.4.2.3 后处理

获得初始稳定形状后,仿真模型在稳定形状的基础上给其中的SPH粒子和球膜节点通过关键字*INITIAL＿VELOSITY施加初速度4m/s,在仿真时不施加阻尼。 以下为冲击过程中两次冲击间隔过程中球膜的应力以及形状变化。

通过球膜的受力情况可知,开始时球顶中心有比较大的应力,之后随着气体扩散,球顶部受力比较均匀,但较大的应力还是集中在球顶和气球底部。当气体和球膜冲击后会造成球膜有比较大形状变化,并由于气体运动的关系和球膜的接触变少,所以此时球膜应力并不大。在浮力的作用下,气体再次上升,会和球膜再一次发生碰撞,这时球顶部和球底部应力较大,通过应力云图发现球底部应力较顶部更大。

取高空气球顶部中心的单元,做出其速度和应力曲线如图17所示。

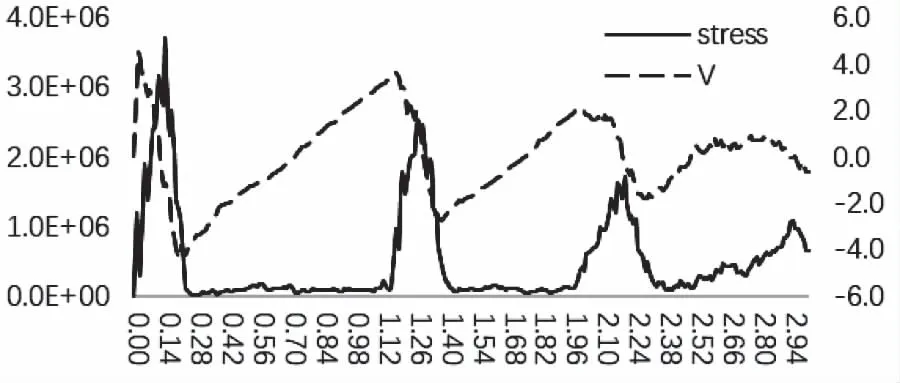
图17 球顶的速度与应力随时间变图

由图中应力和速度曲线可知,在速度下降的同时伴随着球膜应力的上升,说明气体冲击会造成球膜应力增加,同时球膜会降低气体的速度,说明球膜和气体产生了耦合作用。

4 结论

本文以7m3高空气球为例,通过MATLAB和LS-DYNA对高空气球的发放过程中系缆随时间的变化以及受到冲击时球膜形状及应力的变化的进行了模拟。通过MATLAB的数值仿真可以得到系缆的拉力,并可以对高空气球做受力分析,通过运动学方程得到每一时刻高空气球的位置,并得到高空气球每个位置的受力情况,通过LS-DYNA将简化后的模型进行了有限元仿真,并对受到冲击时的球膜的形状及应力变化进行了仿真,通过对比可以得到以下结论:

1)高空气球发放时会产生2～3g的加速度,这时候由于氦气和球膜的初始状态均是静止的,相对速度不大,并且系缆并没有拉紧,初始状态更接近于高空气球做自由上升运动,系缆对球膜的拉力随着高空气球高度的增加逐渐增大,阻力也随着球膜的速度的增大而增大,这样高空气球在阻力和系缆拉力的共同作用下速度上升不会太快,能有效减小到达冲击点时的速度,达到减小冲击的效果。

2)通过LS-DYNA将发放时球膜所受冲击进行仿真,通过应力云图可知气球顶部和气球底部为较大的应力集中区域,而由于球顶部受力面积较大,应力相对较小,而受力更加集中的底部反而是更容易遭到破坏的地方。在以后球顶部中心要加强材料强度,而球底部要加强对球膜的保护,避免应力集中。

在以后计算高空气球发放过程中,可以采用MATLAB数值仿真的方法,改变系缆长度,高空气气球的大小,和充气量的不同,计算不同情况下高空气球的速度峰值。通过LS-DYNA可以仿真小型高空气球球膜应力及形状变化,但难以采用SPH方法对大型高空气球进行模拟,因为随着高空气球的体积增大,网格数量和SPH粒子数量也在增加,导致计算量呈几何级增长,需要找到更加合适的计算方法。