基于差异指标的概念漂移数据流集成分类仿真
柳京秀,梅 颖,卢诚波
(1. 浙江理工大学理学院,浙江 杭州 310018;2. 丽水学院工学院,浙江 丽水 323000)
1 引言
概念漂移[1]是指数据所蕴含的知识或概念随着时间的变化而变化。针对稳定数据流设计的分类方法,不具有抵抗流式数据概念漂移的能力,因此需要有针对性地研究面向概念漂移数据流的分类方法。
根据模型中基分类器的个数,概念漂移数据流分类算法可以分为单分类器算法和集成算法。单分类器算法通常在分类算法中加入增量学习的需求以及遗忘旧数据的功能。Geoff提出了VFDT[2]的算法和CVFDT算法[3],前者只能处理稳定数据流,后者依赖于窗口的大小。H.He提出的解决方案[4]需要在实验开始前设置内核参数,故算法易受到概念漂移的影响。相比单分类算法,集成算法具有更好的泛化能力[5]。其中精度加权集成算法(AWE)[6]和Learn++.NSE[7]算法是经典的集成算法之一。AWE通过当前数据块的性能来设置权重。Learn++.NSE则由基分类器生命周期与分类准确率的变化来计算权重。通过AWE的思想构建的HDWE[1],使用Hellinger距离来修剪集成。AiRStream[8]定期抽样活跃与非活跃基分类器的分类情况来提高模型性能。CALMID[9]设置了集成分类器、漂移检测器、标签滑动窗口等综合的在线主动学习框架。
这些算法在处理分类问题时通常只考虑利用分类准确率作为评判模型分类效果的指标。事实上,只简单地使用某个单一评价指标来评估基分类器的性能,不能全面客观地反映其在集成中的价值。在集成学习中,基分类器的分类性能评价指标是分类器权值调整策略及分类器替换策略的主要依据,因此需要考虑多个指标[10],才能全面反映该基分类器在集成中的整体价值。
基于以上目的,本文提出一种基于差异性综合评价指标的集成算法AE-Div。该算法首先比较样本数据均值来判断当前数据分布是否发生变化;其次利用不一致度量、Kohavi-Wolpert方差作为差异性度量指标来计算集成的差异性,同时结合时间因子、基分类器的分类准确率并以加权的方式融合成“基分类器的综合评价指标”;最后根据概念漂移的检测结果,对基分类器采取不同的调整策略。实验表明,本文提出的算法对比其它算法更具稳定性和适应性。
2 基于差异性度量的集成算法
集成算法由多个基分类器相结合来完成学习任务构建而成,一般结构为:先产生一组基分类器,再利用某种策略将它们结合起来。因此基分类器之间可能存在相关性[11]。如下表1所示,将基分类器C1,C2,C3利用简单投票法策略结合起来,当C1,C2,C3有相同的准确率时,由于(a)中的基分类器具有差异性,故由准确率为66.7%的基分类器组成的集成模型的分类准确率达到了100%;如(b),若由三个完全相同且分类准确率为66.7%的分类器组成,则对集成模型的分类结果没有帮助,其模型准确率仍为66.7%。然而,即使基分类器间具有差异性,由于各个基分类器的分类准确率偏低,同样会影响集成分类器的分类结果,见(c)。因此本文提出一种兼顾准确率和差异性的集成算法,使得集成算法中的基分类器更具独立性、互补性[11]。若数据流发生概念漂移,在集成池中,由于基分类器间具有差异,总有若干个基分类器能更好的应对数据变化。
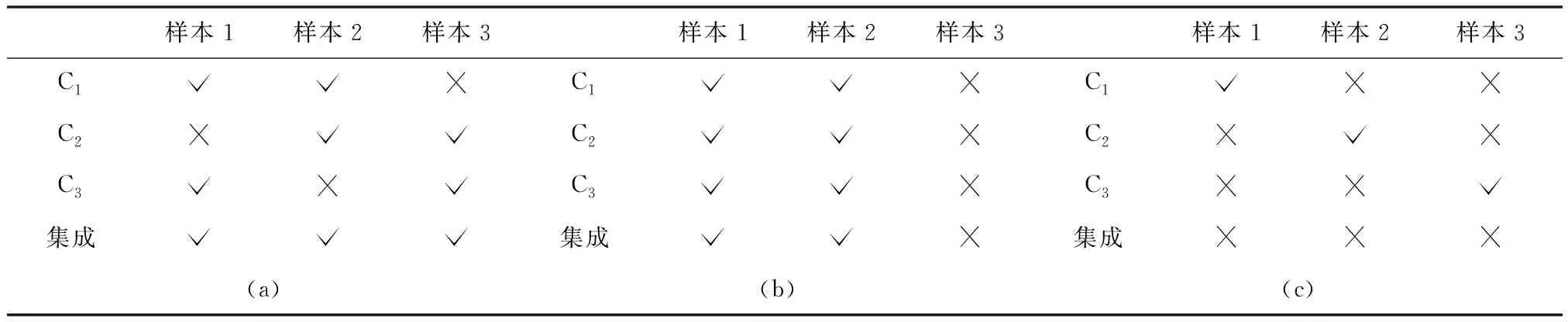
表1 基分类器间的差异性和分类准确性对集成分类结果的影响
2.1 差异性度量指标及权重计算方法
度量差异性的指标有两类[12]:成对度量和非成对度量。成对度量是度量两个基分类器之间的成对相似度或不相似度,然后对所有的成对指标取均值。常用的成对度量有Q-统计量、不一致度量、双错度量等。非成对度量则直接度量集成的差异性。代表性的非成对度量有Kohavi-Wolpert方差、评分者间一致度、熵等。成对度量指标偏重集成分类的局部最优,而非成对度量指标则更强调集成分类的整体最优,因此本文将成对度量和非成对度量作为基分类器的差异性综合评价指标。下面介绍本文选取的度量指标。
不一致度量是指基分类器Ci,Cj给出不同预测结果的样本数目占比,公式如下

(1)
其中:Nab表示分类器Ci分类结果为a,分类器Cj分类结果为b的样本数目,1表示分类结果正确,0表示分类结果错误。根据公式计算,disi.j的值域在[0,1]之间,disi.j值越高,代表两个基分类器的差异性越大。当有T个基分类器参与集成时,集成学习的整体差异性通过求基分类器两两之间的disi.j平均值得到,即
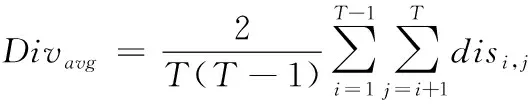
(2)
Kohavi-Wolpert方差源于误差的偏差-方差分解,通过考虑两个基分类器的输出情况来度量差异性,即统计集成E中基分类器对每个样本(xi,yi)的正确分类与错误分类的数目,即
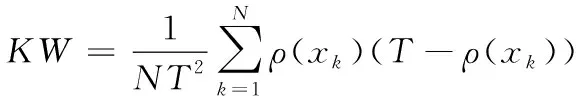
(3)
其中ρ(x)表示对样本(x,y)分类正确的基分类器数目。KW度量的值越大,代表集成差异越大。
当数据分布发生变化时,新分类器与旧分类器不相关,因此本文的权重的设置形式为
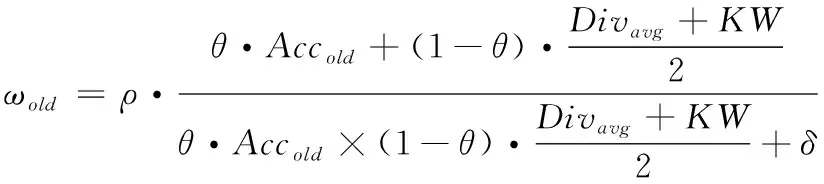
(4)

(5)
其中ρ是权重关于时间的因子。由新数据生成的基分类器在集成E中意义更大,故在模型中增设时间因子。且由当前数据块生成的分类器对该数据块的分类效果最佳,故Acc分别设为
(6)

(7)
其中MSEi为预测误差,MSEr为均方误差。
2.2 AW-Div方法介绍及流程
S1={(x1,y1),…,(xt,yt)},S2={(xt+1,yt+1),…,(xm,ym)}分别表示数据流中的两组样本,其样本总体均值为μ1,μ2。由假设检验可知,若S1,S2服从相同分布,则接受原假设H0:μ1=μ2;否则接受备择假设H1:μ1≠μ2。故本文通过比较两个数据块的样本均值的差异程度来判断数据流是否发生概念漂移。对比其它检测机制更易操作。该检测算法的关键在于阙值的选择。阙值的选择将影响检测机制的结果、基分类器的替换和权重更新的频率,故应根据具体问题来决定阙值的大小。
AW-Div算法步骤可总结如下:
1) 当数据流经缓存区时,按时间顺序将数据块D分成Dold,Dnew两个子数据块,计算两个子数据块的样本均值μold,μnew;
2) 若μold,μnew的变化程度大于漂移阙值,表明当前数据发生概念漂移。将数据块D用K-Means聚成k簇,跳转5);
3) 若μold,μnew的变化程度小于警告阙值,表明当前数据的分布未发生改变,用数据块D按式(4)对旧基分类器进行更新;
4) 若μold,μnew的变化程度在两个阙值之间,说明Dnew中部分数据的分布发生了变化,跳转6);
5) 用K-Means按数据特征将数据聚集成k簇并训练生成k个分类器。用式(5)设置权重;按式(4)对旧基分类器进行更新,跳转8);
6) 用数据Dnew创建基分类器并由式(5)计算其权重,用数据块D按式(4)计算并调整旧基分类器的权重,跳转8);
7) 若集成中基分类器的个数溢出,由分类性能高的基分类器代替过时基分类器;
8) 保留分布发生变化的部分数据与新数据构成数据块D′进入下一轮检测直至结束。
3 仿真研究
本文分别在合成数据集和真实数据集上进行仿真。实验环境如下:Intel UHD Graphics 617GPU,4 GB内存;操作系统为 MacBook Air;仿真环境为基于Python语言的PyCharm平台,编译运行环境为Python3.8。
3.1 数据集
针对AE-Div算法仿真,本文选取了3个人工合成的数据集和3个真实数据集。其中人工合成数据集由ConceptDriftStream构造,真实数据集由UCI数据库获取。具体信息描述见表2。
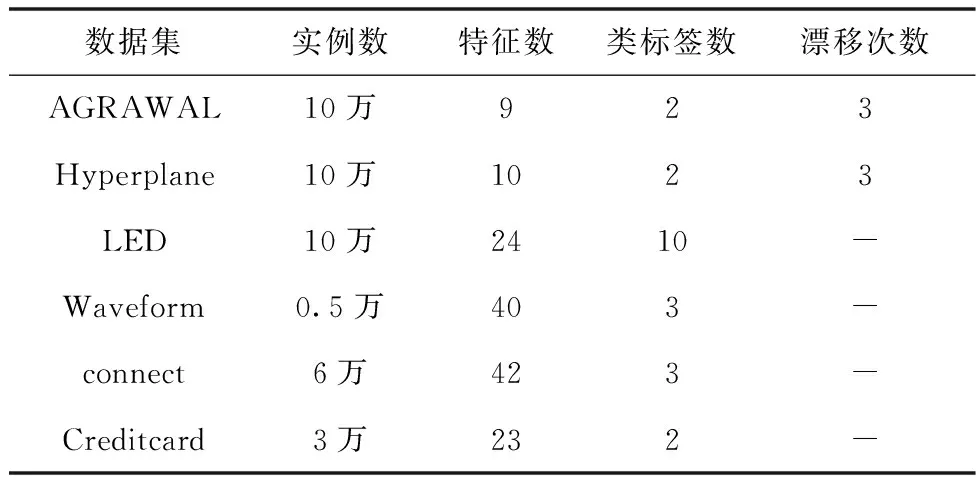
表2 数据集的基本信息
3.2 仿真分析
本文选取AWE、批量增量集成分类器(Batch Incremental ensemble classifier,BIEC)、Learn++.NSE作对比实验。实验统一选取决策树作为基分类器。设置集成分类器的最大容量为30,数据块大小为200,设置AE-Div算法中的参数:ρ=1.1,θ=0.75。
表3为4种算法在6个数据集上运行10次后得到的平均分类准确率,为了方便比较,已将结果转化为百分比。从表中可以看出,在6个数据集上,本文提出的AE-DiV算法的平均分类准确率要优于其它3个算法,且高于其它算法至少7%。为了更详细地展示AE-DiV算法在不同数据集上的对比结果,接下来将分别展示4个算法在不同数据集上实时分类准确率情况。

表3 实验结果
图1、图2分别为4 种算法在AGRAWAL、Hyperplane数据集上的实时分类情况。从图中可以看出,当数据发生概念漂移时,4个算法的分类准确率都受到了影响。由于AE-DiV在每次检测到概念漂移时,会生成适应数据变化的k个新分类器,使模型具有较好分类效果。在AGRAWAL数据集中,当发生第1次、第3次概念漂移时,相比其它算法,AE-DiV更快地恢复分类准确性。从表3可看出,AE-DiV的平均分类准确率最高,其次为BIEC和Learn++.NSE。而在Hyperplane数据集上,AE-DiV的分类效果一直优于AWE、Learn++.NSE。综合表3,对于该数据集,AE-DiV的平均分类准确性最高,其次为BIEC。
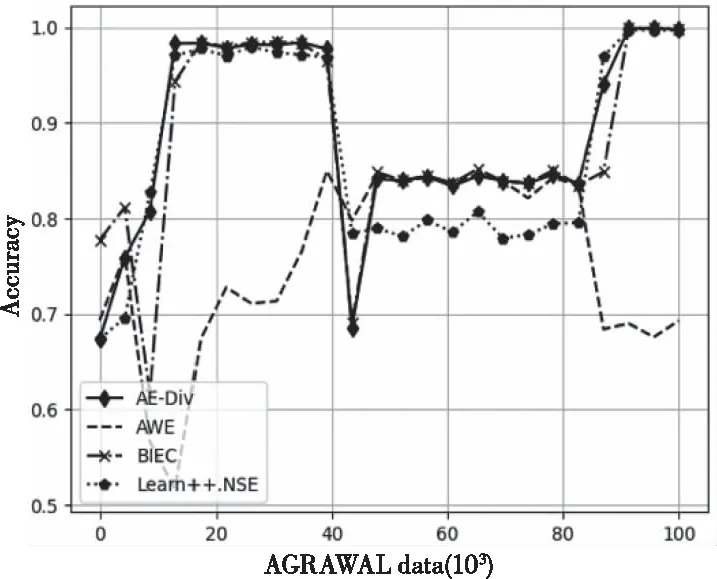
图1 AGRAWAL数据集运行结果
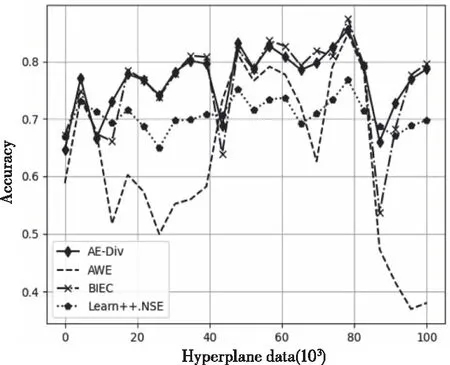
图2 Hyperplane数据集运行结
图3为4 种算法在LED数据集上的分类准确率。由于LED数据分布变化较为缓慢,4个算法都很稳定,AE-DiV、AWE的分类准确率接近90%,Learn++.NSE的分类准确率高于75%,而BIEC的分类准确率只在10%左右。
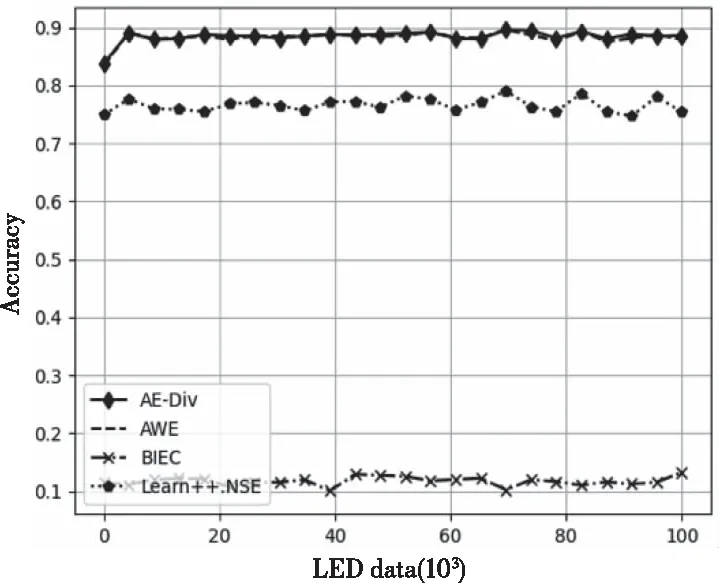
图3 LED数据集运行结果
图4展示了4 种算法在waveform数据集上训练时各个阶段的实时分类准确率。AE-DiV、AWE的分类效果明显优于Learn++.NSE和BIEC,。从表3可以看出,对于waveform数据集,AE-DiV的分类效果最优,其次为AWE。
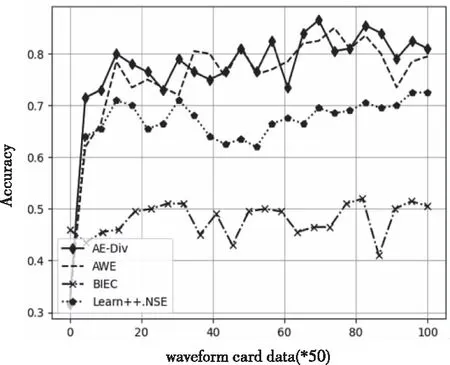
图4 waveform数据集运行结果
图5、图6为 4 种算法在connect数据集、Creditcard数据集上的实时分类准确率。可以看出,当数据分布发生变化时,相对于其它算法的分类效果,AE-DiV均能更快地恢复分类能力,维持较高的分类准确率。结合表3,对于connect数据集,AE-DiV的分类效果最优。对于Creditcard数据集,AE-DiV、BIECE的分类准确率明显优于AWE、Learn++.NSE。
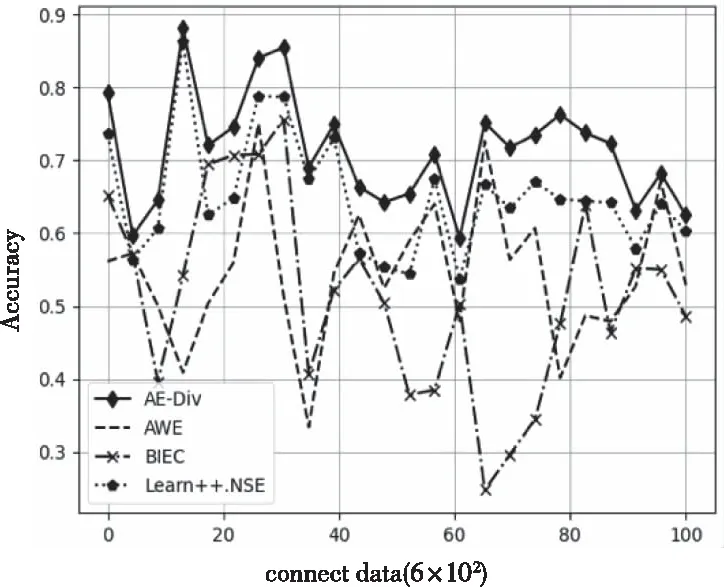
图5 connect数据集运行结果
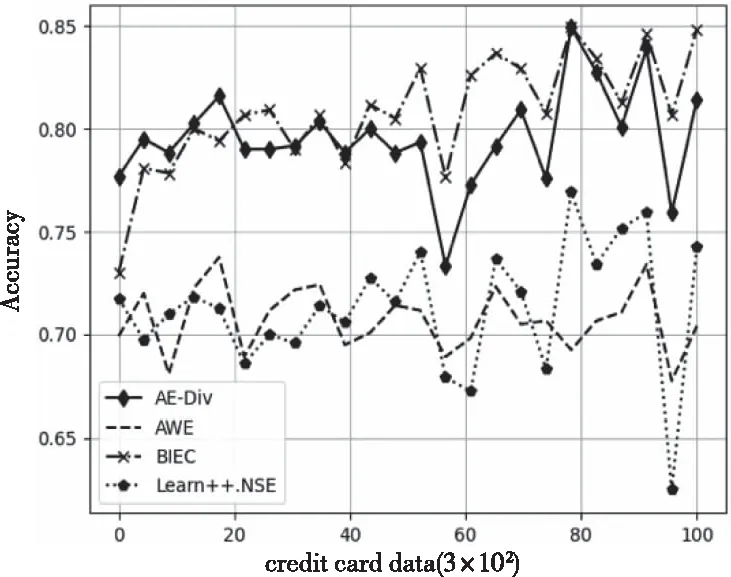
图6 Creditcard数据集运行结果
综合以上可以得出,当测试数据发生变化时,AE-DiV利用新数据训练出新分类器代替过时的冗余分类器调整模型使其更快地适应数据的变化,对比其它算法具有更强的泛化能力和稳定性。
4 总结
本文提出的AE-DiV算法首先通过监测数据块中样本均值的变化来检测数据是否发生概念漂移。该算法仅在数据流分布发生变化时才生成新的基分类器,解决了基分类器在集成模型中的冗余问题。为了使基分类器更好的处理概念漂移,将基分类器的分类准确率和差异性与时间因子相结合融合成权重对模型进行优化。最后与其它几种概念漂移分类算法进行仿真实验,结果表明AE-DiV模型具有更好的分类准确性和稳定性,能更快地适应概念漂移。

