起竖臂桁架的结构优化设计
贾学军,毛利民,贾永涛,曾文应
(1.北京航天发射技术研究所,北京100076;2.航天系统部装备部军代局驻北京地区第二军代室,北京100081;3.北京航空航天大学宇航学院,北京100191)
1 引言
空间桁架结构由于具有自重轻、造价低廉和施工简单等诸多优点,广泛应用于起重、起竖设备等诸多领域。采用优化方法对桁架结构进行结构优化设计可极大地提高其强度、刚度并减轻其自身重量,在工程上具有重要的实际应用价值。
结构拓扑优化一直是优化领域中的热点与难点。自上世纪以来,国内外许多学者就结构拓扑优化展开了大量的研究,并取得了丰富的成果。1904年Michell对桁架结构优化进行研究,并提出了Michell准则[1]。1964年,Dorn等提出了基结构法[2]。之后,谢亿民提出了渐进结构优化法(Evolutionary Structural Optimization, ESO),其基本概念就是通过将无效或低效的材料逐渐去除,从而使结构趋于优化[3]。而在另一个方向上,Bendsoe和Kikuchi提出了均匀化方法[4],开辟了连续体拓扑优化的方向。在此基础上,程耿东等人对变厚度法展开了研究与应用[5],Mlejnek建立了变密度法模型[6]。隋允康等人又创立了基于ICM方法的拓扑优化方法[7]。
按照结构形式划分,工程结构大体可以分为两类:一类为桁架、刚架等形式的杆系结构;另一类为板、三维实体等形式的实体结构。针对这两种不同的结构形式,结构拓扑优化设计又分为杆系结构的离散体拓扑优化设计和连续结构的连续体拓扑优化设计。
起竖臂显然是一种空间桁架结构,对其进行结构拓扑优化本应采用离散体拓扑优化方法。但现有的空间桁架结构的离散体拓扑优化方法是凭借先验知识确定桁架的构型、节距等参数,并用杆件将各节点两两相连作为基结构。然后从基结构出发,利用对各杆件的参数优化方法确定各杆件的有无,从而完成空间桁架结构的拓扑优化。显然,这种方法在确定基结构时就受到设计人员设计经验的影响,难以避免人的主观随意性。如果桁架的基结构选取不好,最终也难以获得满意的优化结果。
连续体的拓扑优化能够在已知边界和载荷条件下确定最佳形状设计方案,在产品研制初期的概念设计阶段具有重要的指导意义。基于上述考虑,本文将首先构造起竖臂桁架的连续体基结构,然后采用连续体拓扑优化方法对构造的起竖臂桁架的连续体基结构进行拓扑优化,获取杆件优化布局后的桁架结构,然后再在拓扑优化结果的基础上,进一步对桁架结构中的杆件进行截面参数优化,以期实现对起竖臂桁架结构的优化设计。
2 起竖臂的结构优化
起竖臂原始设计结构如图1所示,材料为Q345钢。其上有预先规划的外部载荷作用区和自身所需的支撑区,在有限元模型中分别作为载荷施加区域和边界约束区域。工作过程中,起竖臂要经历起竖、运输垂向载荷、运输横向载荷及运输纵向载荷四种工况。各工况下的载荷及边界条件见表1。对起竖臂的优化设计将在上述四种工况下进行。

表1 工况汇总表
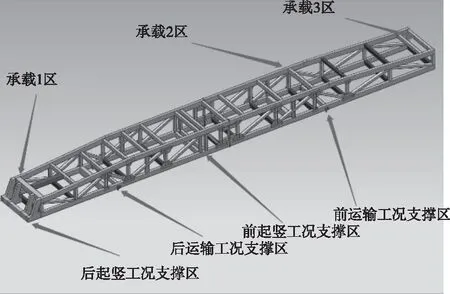
图1 起竖臂原始设计结构
2.1 拓扑优化
参考起竖臂的原始设计结构,起竖臂是由四根弦杆及位于弦杆之间的各种腹杆构成。每两根相邻的弦杆和其间的腹杆都在一个平面内,可以假想这些杆件是从一个完整的平板上“挖出”来的结构。由此,我们可以先恢复这些平板结构,构造一个如图2所示的由四个平板围成的方形筒体结构作为起竖臂的连续体基结构,筒体的尺寸与起竖臂原始设计结构的外形轮廓尺寸一致,为2000mm×3300mm×35200mm,与原始设计结构对应的载荷区及支撑区作为冻结区域予以保留。在此基础上,根据连续体结构拓扑优化理论科学地删减筒体四个平板的材料,进而获得材料的最优布放路径,并据此设计优化的起竖臂结构。基结构板厚的取值应足够大以保证基结构有足够的刚度和强度,在满足上述条件的前提下,板厚的具体取值对拓扑优化结果的影响不大[8],这里取板厚度为100mm。
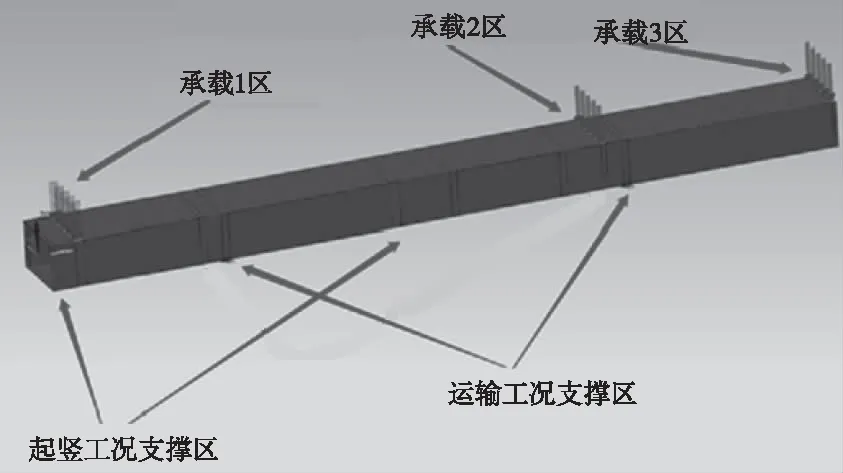
图2 起竖臂连续体基结构
目前,连续体拓扑优化方法中较为成熟且应用较多的主要有均匀化方法、变密度法。变密度法[9]是从均匀化方法发展而来的,以有限元模型中的每个单元的相对密度值(取值介于0~1之间)为设计变量,直接定义一个经验公式来表达密度与弹性模量间假定的函数关系[10],这样结构的拓扑优化问题就被转换为材料的最优分布问题。其实质是将拓扑变量依附于单元材料的密度上以便应用基于连续变量的优化算法。变密度法设计变量少,程序实现简单,在工程应用中得到了广泛的重视和研究,是目前算法上便于实施且应用较多的一种拓扑优化方法。本文将基于这一方法利用TOSCA软件完成起竖臂连续体基结构的拓扑优化。
拓扑优化是以四种工况下的结构应变能之和最小为优化目标,以各载荷作用区最大位移不超过35mm以及结构优化后与优化前的体积比不大于0.2为约束条件。
优化的过程即是调整各单元相对密度的过程,得到的优化结果自然以最终的材料相对密度分布云图表示,见图3。图中,若材料相对密度较高,则该处材料的弹性模量也较高,这部分材料对提高结构刚度有益,应予以保留。反之,若材料相对密度较低则意味着该处材料空心率较高且弹性模量非常小,这部分材料对提高结构抵抗由外力引起的弹性变形的贡献极小,可以从结构中删除。
按照“如果结构某部位材料的相对密度低于0.1,则该处材料即可删除”的原则对拓扑优化结果进行过滤处理,得到剩余结构如图4所示。

图4 起竖臂基结构拓扑优化后的剩余结构
根据拓扑优化结果显示的材料布局形式,经适当规整,便得到了一个新的、经拓扑优化的桁架结构,见图5。该结构只是拓扑优化后的桁架结构的概念设计,可在该结构基础上对其进行有限元建模以便进一步分析和优化。
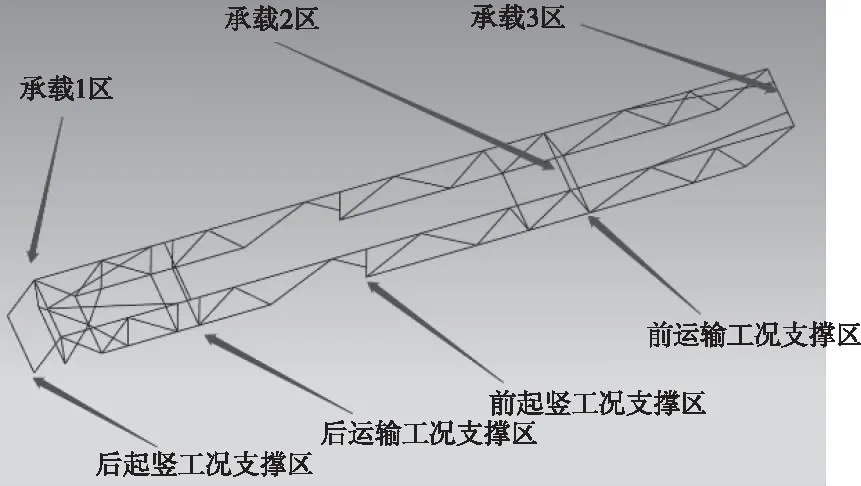
图5 桁架拓扑优化结构的概念设计
2.2 截面参数优化
上一节从连续体基结构出发经连续体拓扑优化得到的桁架拓扑优化结构的概念设计只是整个优化过程中的一个初步结果,它仅指明了杆件的布放路径,但未指明在布放路径上放置什么样的杆件,即在布放路径上的杆件截面尺寸应是什么样的。因此,接下来还需在桁架拓扑优化结构概念设计的基础上进行桁架杆件截面尺寸的参数优化。
杆件截面尺寸的参数优化是基于UG NX自带的几何优化模块进行,该模块可以对结构进行多变量多工况优化,也能对多个变量进行全局灵敏度分析。在前面的拓扑优化设计中,将材料相对密度大于0.1的结构都予以保留。由于0.1这个临界值较低,可能导致并非真正需要的杆件“混入”拓扑优化的结果中,拓扑优化结果中的一些“似是而非”的杆件可作为存疑杆件。在正式进行尺寸优化之前,可先对存疑杆件进行全局灵敏度分析,以确定对它们的取舍。
对于概念设计中各杆件的截面尺寸,可根据剩余结构中杆件的尺寸对其进行粗略的分组并大致确定各组截面尺寸参数的初值。优化以各组截面尺寸参数为设计变量;以桁架总质量最小为目标;以桁架在所有工况下最大位移不超过35mm,最大应力不超过100MPa为约束条件。
经灵敏度分析和参数优化后便可得到图6所示的新桁架结构。需要说明的是,由于桁架的拓扑结构是从基结构的平板中“挖出来的”,桁架中各杆件的截面形状均为实心的矩形,所谓的截面尺寸优化实际上就是对矩形的二个边长进行优化。可依据设计要求,按截面抗弯刚度相当的原则选取要求的型材加以替换。本文按设计要求以方钢管替换实心矩形截面杆件,最终得到的优化后起竖臂结构质量为16.97t,相较于原结构30.78t的质量,减重效果显著。

图6 优化后的起竖臂结构
图中起竖臂优化结构的所有梁结构根据截面尺寸划分为10组,各组截面尺寸分别为:
50mm×100mm×5mm(粉)
100mm×100mm×4mm(红)
250mm×150mm×8mm(棕)
250mm×250mm×10mm(黄)
400mm×250mm×12mm(蓝)
600mm×400mm×16mm(银)
150mm×150mm×4mm(浅蓝)
400mm×400mm×10mm(紫)
250mm×150mm×5mm(绿)
600mm×400mm×8mm(黑)
3 起竖臂优化结构的重分析
为全面、深入考察优化设计效果,在全部四种工况下,对原始设计和优化后的起竖臂结构进行了对比分析,结果汇总于表2。对比分析结果表明,四种工况下原结构和优化结构的最大位移均发生在起竖工况,最大位移点均位于承载3区,二者的位移云图见图7和图8。原结构的最大Von Mises应力发生在运输垂向载荷工况,最大应力点位于后端的运输工况支撑区;优化结构的最大Von Mises应力发生在运输横向载荷工况,最大应力点位于承载3区。二者的应力分布云图如图9和图10。限于篇幅本文仅给出二者最大位移工况和最大应力工况的对比云图。

表2 起竖臂优化结构重分析汇总表

图7 原结构起竖工况位移云图
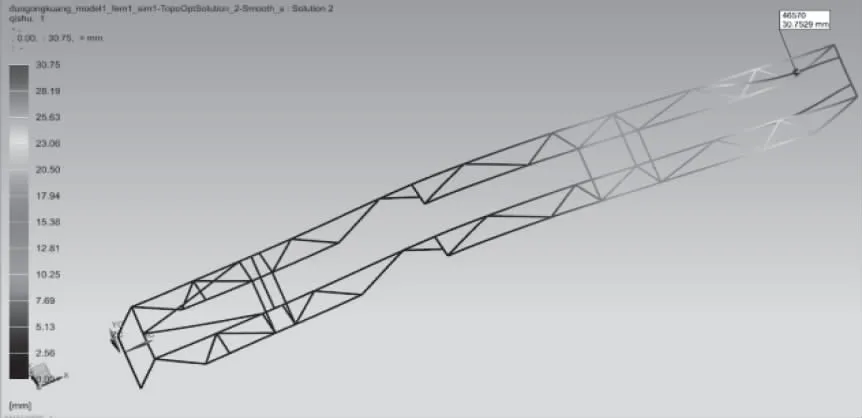
图8 优化结构起竖工况位移云图
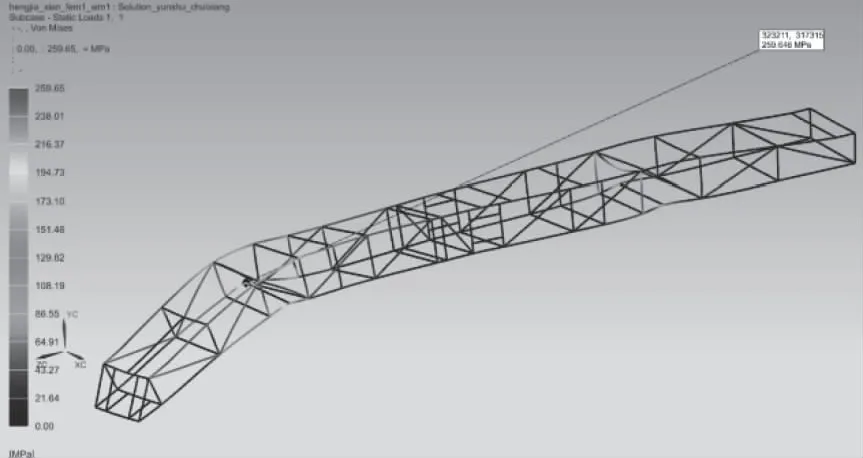
图9 原结构垂向载荷工况应力云图
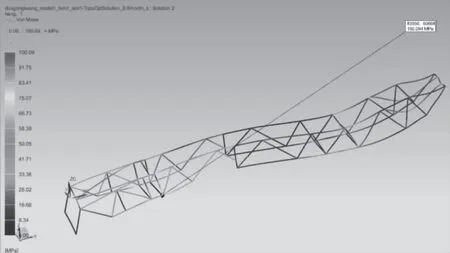
图10 优化结构横向载荷工况应力云图
4 起竖臂优化结构的线性屈曲分析
由于优化过程中没有施加保证结构稳定性的约束条件,优化出的结构中可能会存在细而长的受压杆件,难以满足结构稳定性要求。为此,需对优化结构在全部工况下进行屈曲分析。分析结果表明:全部工况下,一阶特征值最低为5.706,发生在运输横向载荷工况下,屈曲模态如图11所示。由于各工况下结构的特征值都远大于1,可以认为新的起竖臂结构具有良好的稳定性。
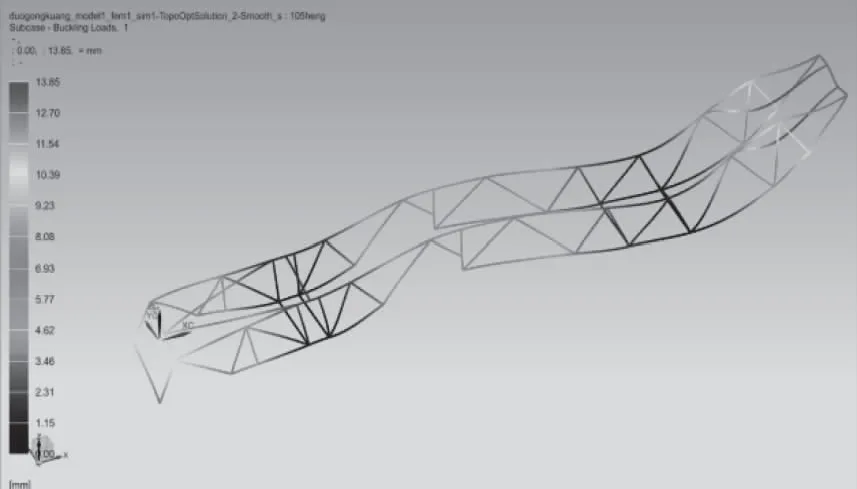
图11 横向载荷工况优化结构屈曲响应分析
5 结论
本文介绍了依次使用基于连续体拓扑优化方法和参数优化方法,对起竖臂桁架结构进行优化设计的完整流程。与原结构在各工况下的对比分析表明,本文方法能够在提高结构刚度和强度的同时,有效降低结构质量,是一种行之有效的起竖臂结构优化设计方法,可在实际工程设计过程中参考使用。

