核心素养导向下的初中数学试卷讲评课探究
陈桂玲

一、借助大数据精准把握学情,提高讲评针对性
借助大数据,可以清晰了解学生在考试中的答题情况。笔者所在学校运用希沃评卷系统,通过系统平台上的数据可以清晰地看到每个班的平均分,各小题的平均分及得分率,每个学生每個小题的得分等,个体与整体的对比情况一目了然。借助大数据,教师在课前能有效地备学情、备教法,把握好课堂讲解的重点和需要突破的难点,在试卷讲评课中做到精准教学。大数据充分暴露学生的思维弱项,教师在备课中针对该思维弱项设计一题多变,讲清知识的本质。
二、试卷讲评之课前功夫,强基提能
1. 教师提个性化要求,生生在互助纠错中强基
每次考试结束,笔者会将学生的问卷收回来,并根据学生的数学测评数据,圈出一些在学生发展区内能做出来的错题。学生准备一个错题本,教师要求学生寻找同学进行交流,将错题进行纠正,充分发挥学生之间的互帮互助精神。一方面,学生得到个性化辅导,在争辩中明理,在合作中进步,及时弥补知识漏洞;另一方面,教师能腾出更多的课堂时间去讲解重点、突破难点。
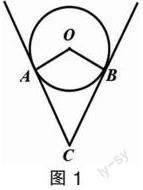
例1(试题第7题) 一根钢管放在V形架内,其横截面如图1所示,钢管的半径是24cm,若∠ACB =60°,则劣弧AB的长是( ).
A.8πcm B.16πcm
C.32πcm D.192πcm
本题的得分率是66.7%,得分率较高,但这类基础题应该具备更高的得分率。学生做错的原因主要是:忘记弧长公式,不会应用切线长定理。对于这类基础且重要的题型,笔者让答错的学生组成一个小组,小组长视情况邀请教师加入指导。学生们在课下自主复习弧长公式的推导和应用、切线长定理的证明,接着小组间合作交流解题思路、答题错误的原因。通过教师的适当点拨,学生能够从知识点、解题方法、错因分析三个方面全方位探究这类基础题所涉及的知识与能力,在交流互助中强化基础,掌握学习方法。
2.教师点拨探究方向,生生在互动探究中提能
在课前,对于重点部分,教师鼓励学生进一步去探究,对题目进行一题多解、一题多变;对于难点部分,教师在解题思路上适当点拨,然后引导学生之间互相探讨。教师不直接告诉学生答案,先跟学生一起探讨解题思路,让学生觉得自己努力一下就可以解决问题,这样更能激发学生的学习兴趣、激励更多的学生参与到探究中来,更好地让学生产生思维的碰撞,从而擦出思维的火花,收获更大的成就感。
例2 (试题第25题第(2)小问)如图2,⊙O的直径AB=10,弦AC= 8,连接BC.
(1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)
(2)在(1)所作的图中,求四边形ABCD的周长.
分析:本题第(2)问的得分率是35.6%,属于得分率较低的题目。这类题不适合直接丢给学生小组自主学习交流。教师需要根据阅卷情况,在课堂上给学生分析解题误区,并给予适当点拨后,安排学生合作探究。本题解题的关键是求AD的长。针对该题,教师先告知学生,他们的答题误区主要体现为“知道要求AD的长,但不会大胆添加辅助线”。接着,教师跟学生一起分析题目的条件,CD=BC有什么用?此时,学生会想到连接OC,教师及时鼓励。但学生发现仅仅连接OC依然不能解决问题。于是,教师顺势提醒学生还需要继续添加辅助线,学生通过回想圆中常用的辅助线添加技巧,不难想到连接BD。最后,教师点拨学生利用垂径定理、勾股定理、中位线等知识构造方程求线段长。
三、试卷讲评之一题多变,揭本求源
在课前的互动环节中,学生基本能纠正试卷上的错题,但他们的认知可能只停留在知识的表面,没有深入理解解题的思路与具体的解题方法,也没有深化错题的多种解题技巧,特别是考察综合能力较强的题目,如果不能真正理解题目当中考查的初中数学思想与方法,就不能达到触类旁通的效果,不能让孩子们真正地了解数学知识重点、难点中所蕴含的深层含义。因此,对于重难点题目,教师要在课堂上对题目进行一题多变,充分发散学生的思维,开发学生的全方位思考能力,提高学生的综合解题能力。
四、试卷讲评之提炼模型,点睛升华
在试卷讲评课中,教师精选典型题目,通过对题目进行横向比较或纵向拓展,揭示题目的本质。
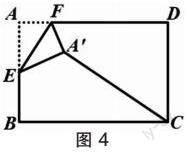
例3(试题第16题)如图4,在矩形纸片ABCD中,AB=4,AD=6,点E是AB的中点,点F是边AD上的一个动点,将ΔAEF沿EF所在直线翻折,得到ΔA′EF,则线段A′C的最小值是 .
分析:这是一道隐圆中的动点求最值问题,属于综合性较强的题目。点F是主动点,点A′是从动点,其中点E是定点,AE=A′E,点A′的运动轨迹是一个以E为圆心,AE为半径的圆。
教师可抽离出题目本身,先跟学生分析“圆上的动点到圆外某一定点间的距离”问题。如图6,在平面内,点E是⊙O上的一个动点,点D是圆外的一点,当E、O、D三点共线时,线段DE有最值。当运动到如图8的位置时,DE有最大值,当运动到如图8的位置时,DE有最小值。
根据上面的分析,如图4,当E、A′、C三点共线时,此时线段A′C有最小值,最小值是CO-CA′,即210-2。教师在细致严谨评讲完这道题以后,马上布置一道类似的题目,进行即时训练。以此来检验教师的教与学生的学是否达成目标。
五、试卷讲评之化静为动,提质增效
教师借助信息技术,如几何画板,可以把动点问题,旋转问题等抽象问题形象生动地展现给学生,真正做到课堂以生为本,发展学生的核心素养。如例3,利用几何画板,通过拖动点F,然后跟踪动点A′的运动轨迹,形象地呈现出点A′的运动轨迹是一个以点E圆心,AE为半径的一个圆。现在就容易理解了,当E、A′、C三点共线时,此时线段A′C有最小值。借助几何画板,能化静为动,为数学的课堂教学提质增效。又如,在数学课堂上,对知识的梳理、解题方法的总结,以及数学模型的提炼等,也可以利用信息技术来制作成生动形象的课件,直观简洁地呈现出来,能帮助学生快速理解知识,提升他的数学核心素养。
【本文系广州市增城区教育科学规划2021年度课题“基于大数据的精准教学互动模式在试卷讲评课的应用研究”(课题编号zc2021 085)研究成果】
责任编辑 徐国坚

