2023年中考数学模拟卷

初中数学教研核心团队

（试卷满分150分 考试时间120分钟）

一、选择题（每小题3分，共30分）

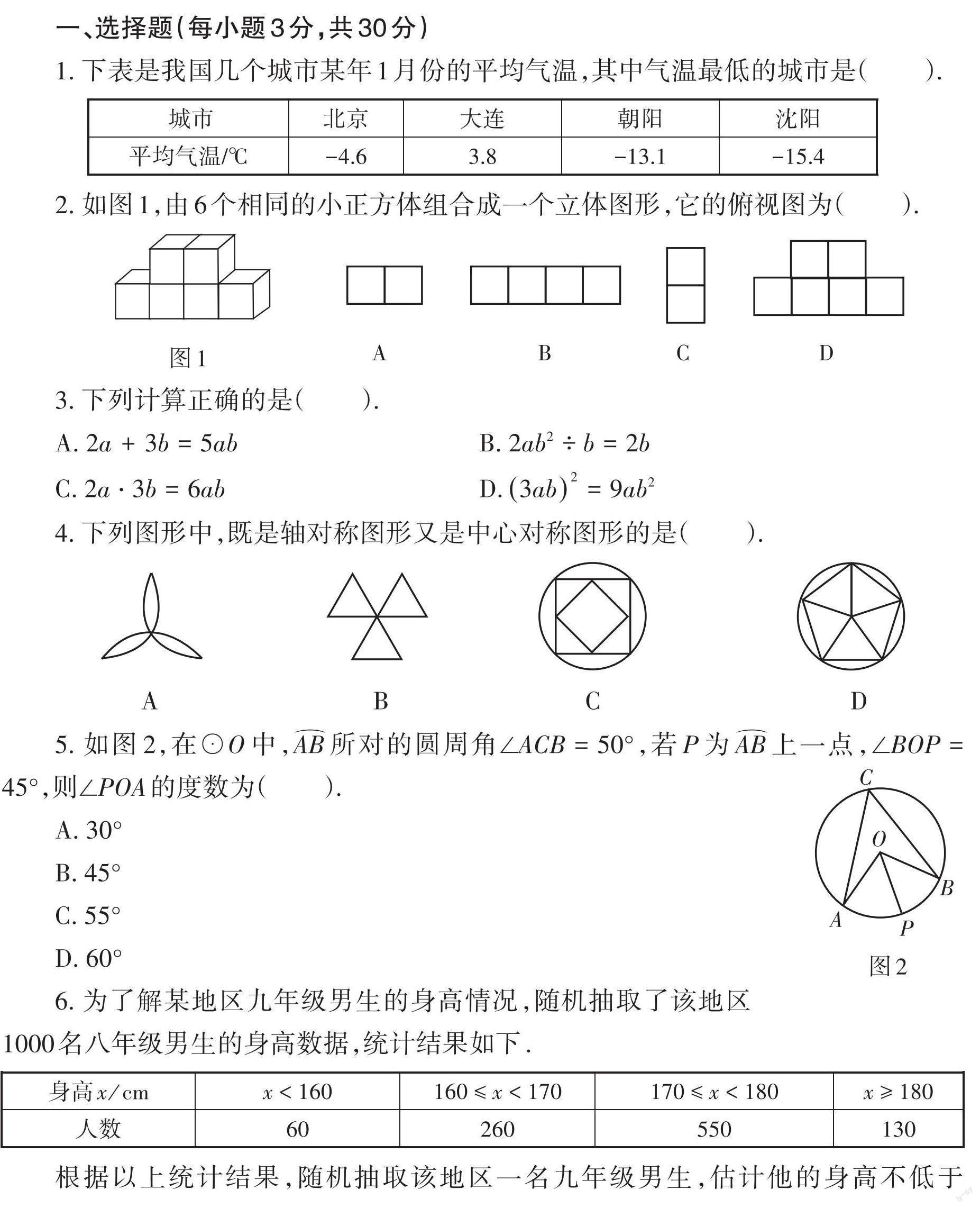
1. 下表是我国几个城市某年1月份的平均气温，其中气温最低的城市是（_____）.

[ 城市 北京 大连 朝阳 沈阳 平均气温/℃ -4.6 3.8 -13.1 -15.4 ]

2. 如图1，由6个相同的小正方体组合成一个立体图形，它的俯视图为（_____）.

3. 下列计算正确的是（_____）.

A. [2a+3b=5ab] B. [2ab2÷b=2b]

C. [2a?3b=6ab] D. [3ab2=9ab2]

4. 下列图形中，既是轴对称图形又是中心对称图形的是（_____）.

5. 如图2，在⊙O中，[AB]所对的圆周角∠ACB = 50°，若P为[AB]上一点，∠BOP = 45°，则∠POA的度数为（_____）.

A. 30°

B. 45°

C. 55°

D. 60°

6. 为了解某地区九年级男生的身高情况，随机抽取了该地区1000名八年级男生的身高数据，统计结果如下.

根据以上统计结果，随机抽取该地区一名九年级男生，估计他的身高不低于[170 cm]的概率是（_____）.

A. 0.32                      B. 0.55                     C. 0.68                        D. 0.87

7. 如图3，Rt△ABC中[，∠ABC=90°]，根据尺规作图的痕迹判断以下结论错误的是（_____）.

A. [DB=DE]

B. [AB=AE]

C.  [∠DAC=∠C]

D. [∠EDC=∠BAC]

8. 如图4，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内）. 已知AB = a，AD = b，∠BCO = x，则点A到OC的距离等于（_____）.

A. asin x + bsin x B. acos x + bcos x C. asin x + bcos x D. acos x + bsin x

9. 如图5，在Rt△ABC中，∠C = 90°，∠BAC = 45°，点O在AB上，经过点A的⊙O与BC相切于点D，交AB于点E，若CD = [2]，则图中阴影部分的面积为（_____）.

A. 4 - [π2]    B. 2 - [π2] C. 1 - [π4]  D.  2 - π

10. 如图6，边长为1的正方形ABCD中，点M从点A出发以每秒1个单位长度的速度向点B运动，同时点N从点A出发以每秒3个单位长度的速度沿A—D—C—B的路径向点B运动，当一个点到达点B时，另一个点也随之停止运动. 设△AMN的面积为S，运动时间为t秒，则能大致反映S与t的函数关系的图象是（_____）.

二、填空題（本题共6小题，每小题4分，共24分）

11. 原子很小，[1]个氧原子的直径大约为[0.000 000 000 148 m]，将[0.000 000 000 148]用科学记数法表示为__________.

12. 若方程[ax2+x-1=0]有两个不相等的实数根，则[a]的取值范围是__________.

13. 不等式组[5x-1>3（x+1） ，12x-1≤4-13x]的解集为__________.

14.将正三角形、正四边形、正五边形按如图7所示的位置摆放，如果∠3 = 32°，那么∠1 + ∠2= __________°．

15.小华和小苗练习射击，两人的成绩如图8所示，小华和小苗两人成绩的方差分别为[s21]，[s22]根据图中的信息判断两人方差的大小关系为__________．

16. 如图9，在等腰三角形ABC中，AC = BC = 4，∠C = 120°，点D为AC的中点，点E为边AB上一个动点，连接DE，将△ADE沿直线DE折叠，点A落在点F处. 当直线EF与直线AC垂直时，则AE的长为__________.

三、解答题  （第17、 18、19题每题8分，第20题11分，共35分）

17. 先化简，再求值：（x + 1）2 - （x + 2）（x - 2），其中[5

18. 如图10，已知在四边形ABCD中，点E在AD上，∠BCE = ∠ACD = 90°，∠BAC = ∠D，BC = CE.

（1）求证：AC = CD；

（2）若AC = AE，求∠DEC的度数.

19. 如图11，点A（1，a）在反比例函数[y=3x]（x > 0）的图象上，AB垂直于x轴，垂足为点B，将△ABO沿x轴向右平移，得到Rt△DEF，且OF = 2OB，点D落在反比例函数[y=kx]（x > 0）的图象上.

（1）求点A的坐标；

（2）求k值.

20. 在阳光大课间活动中，某校开设了立定跳远、实心球、长跑等体育项目. 为了了解九年一班学生的立定跳远成绩的情况，对全班学生的立定跳远测试成绩进行统计，并绘制了以下不完整的频数分布直方图和扇形图，如图12，根据图中信息解答下列问题.

（1）求九年一班学生总人数，并补全频数分布直方图（标注频数）；

（2）求2.05 ≤ a < 2.25成绩段在扇形统计图中对应的圆心角度数；

（3）已知九年一班在2.25 ≤ a < 2.45成绩段中有男生3人、女生2人，现要从这5人中随机抽取2人参加学校运动会，请用列表法或画树状图法求出恰好抽到一男一女的概率.

四、解答题（每题11分，共33分）

21. 如图13，1号楼在2号楼的南侧，两楼高度均为90 m，楼间距为AB. 冬至日正午，太阳光线与水平面所成的角为32.3°，1號楼在2号楼墙面上的影高为CA；春分日正午，太阳光线与水平面所成的角为55.7°，1号楼在2号楼墙面上的影高为DA. 已知CD = 42 m.

（1）求楼间距AB；

（2）若2号楼共30层，层高均为3 m，则点C位于第几层？（参考数据：sin 32.3° ≈ 0.53，cos 32.3° ≈ 0.85，tan 32.3° ≈ 0.63，sin 55.7° ≈ 0.83，cos 55.7° ≈ 0.56，tan 55.7° ≈ 1.47）

22. 如图14，在⊙O中，点P为[AB]的中点，弦AD，PC互相垂直，垂足为M，BC分别与AD，PD相交于点E，N，连接BD，MN.

（1）求证：N为BE的中点.

（2）若⊙O的半径为8，[AB]的度数为90°，求线段MN的长.

23. 一玩具厂去年生产某种玩具的成本为10元/件，出厂价为12元/件，年销售量为2万件．今年计划通过适当增加成本来提高产品档次，以拓展市场．经市场调研可知，若每件玩具的成本提高0.7倍，出厂价比去年相应提高0.5倍，则销售量可提高一倍.现预计今年年销售量将比去年年销售量提高x倍（0< x ≤1）．

（1）用含x的代数式表示今年生产的这种玩具每件的成本为__________元，每件玩具的出厂价为__________元．

（2）设今年这种玩具的年销售利润为w万元，求当x为何值时，今年的年销售利润最大. 最大年销售利润是多少万元？

五、解答题（每题14分，共28分）

24. 已知：点D是等腰直角三角形ABC斜边BC所在直线上一点（不与点B重合），连接AD．

（1）如图15①，当点D在线段BC上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE. 求证：BD = CE，BD⊥CE．

（2）如图15②，当点D在线段BC延长线上时，探究AD，BD，CD三条线段之间的数量关系，写出结论并说明理由.

（3）若BD = [3]CD，直接写出∠BAD的度数．

25.二次函数[y=x2-2mx+m2-4]与x轴交于A，B（A在B左侧），与y轴交于C，抛物线的对称轴交x轴于E. 过C作x轴的平行线，交抛物线于D.

（1）当m = -1时，探究AB与CD的数量关系，请写出探究过程.

（2）当m = 3时，（1）中的结论_______（直接填“成立”或“不成立”）.

（3）四边形CDEA能否为平行四边形？若能，求出此时m的值，若不能，请说明理由.