某皮卡后驱动桥壳强度的计算校核及仿真

卫 锋

Wei Feng

（壁虎新能源汽车科技有限公司，广东 深圳 518000）

皮卡作为客货两用型汽车，近5年来销量逐年上升，后驱动桥是其最重要零部件之一，本文对某款皮卡车型后驱动桥的选型和设计进行计算分析。

1 后驱动桥功用[1]

后驱动桥可将发动机扭矩通过主减速器、差速器、半轴等传动装置传递到驱动轮，实现减速增扭；同时，后驱动桥通过主减速器圆锥齿轮副改变扭矩的传递方向，并通过差速器实现内、外侧车轮转向时具有不同转速。

2 驱动桥类型

国内皮卡车型的后驱动桥主要以非断开式结构为主，如图1 所示，并辅以鼓式或盘鼓式制动器的轮边结构。

图1 非断开式后驱动桥（半轴部分）

3 计算校核[2-3]

某皮卡车型的基本参数见表1。

表1 某皮卡车型基本参数

3.1 桥壳静弯曲应力计算

将后驱动桥视为简支梁结构，其受力如图2所示。

图2 后驱动桥简支梁结构的受力分析

此时桥壳在两钢板弹簧座之间的静弯矩最大，计算式为

式中：M静弯max为简支梁结构下后驱动桥壳的最大静弯矩。

由于车轮质量远小于后驱动桥质量，且初始设计时车轮质量无法准确估计，所以式（1）中可忽略g2，将表1中数值代入式（1）计算得

危险断面处桥壳的垂向弯曲截面系数W弯为

将表1中数值代入式（2）计算得

后驱动桥壳的静弯曲应力δ静弯为

将上述计算值代入式（3）计算得

δ静弯=4299750 Nmm/61020 mm3=70.5 N/mm2

后驱动桥壳的材质为16ML 或09SiVL，此材料的应力[δS]=400 N/mm2，则安全系数n为

将上述数值代入式（4）计算得

一般推荐安全系数大于4，由此判定此款后驱动桥壳的静弯曲强度安全可靠。

3.2 不平路面下桥壳强度计算

当汽车行驶在不平路面时，桥壳除了承受静止状态下的载荷外，还承受路面冲击载荷，此时桥壳的动应力为

式中：δ动弯为后驱动桥壳的动弯曲应力；K动为动载荷系数，通常载货汽车的动载荷系数为2.5。

将数值代入式（5）计算得

δ动弯=2.5×70.5 N/mm2=176.25 N/mm2

此时，δ动弯＜[δS]=400 N/mm2,由此判定动载荷作用下桥壳强度安全可靠。

3.3 紧急制动时桥壳强度计算

皮卡满载时紧急制动，其整车受力分析如图3所示，其中Far、Fbr分别为紧急制动时地面对前、后轮的摩擦力；N1为地面对前轮的法向作用力，N2为地面对后轮的法向作用力；a满为满载时汽车紧急制动的减速度。

图3 紧急制动整车受力分析

地面对后驱动桥左、右车轮的垂向作用力为N2L、N2R，二者大小相等，则

将式（7）代入式（6）得

由式（8）得Δ=1-根据经验本文Δ取值0.85。

汽车紧急制动时，后驱动桥壳的受力分析如图4所示。

图4 紧急制动后驱动桥壳受力分析

以后驱动桥最大载荷这一极限工况计算桥壳在两钢板弹簧座间的垂向弯矩Mv和水平方向弯矩Mh，则

式（9）中忽略g2，将各数值代入式（9）、（10），计算得

桥壳在两钢板弹簧座外侧同时承受制动力矩T，即

将各数值代入式（11）计算得

由式（9）～（11）得到紧急制动时后驱动桥壳的弯曲合成扭矩M合为

即

综上，紧急制动时后驱动桥壳的弯曲扭矩应力δ弯为

即

桥壳设计状态下的危险断面处的扭转弯曲截面系数W扭为

即

W扭=2×8 mm ×(96 mm-8 mm)2=123904 mm3

由紧急制动引起的扭转应力δ扭为

即

则在后驱动桥壳危险断面处弯曲和扭转的合成应力为

即

计算结果表明，δ合＜ [δS]=400 N/mm2，由此判定紧急制动工况下后驱动桥壳强度安全可靠。

3.4 最大牵引力下桥壳强度计算

当汽车以最大牵引力行驶时，其受力分析如图5所示。

图5 最大牵引力下整车受力分析

图5中最大牵引力Fmax的计算式为

将各数值代入式（17）计算得

皮卡满载时以最大牵引力行驶，后驱动桥壳的受力分析如图6所示。

图6 以最大牵引力行驶后驱动桥壳受力分析

后驱动桥壳在两钢板弹簧座间的垂向弯矩Mv′和水平方向弯矩Mh′分别为

式中：Δ′为以最大牵引力行驶时质量转移系数；g2可忽略不计。

即

则

桥壳在两钢板弹簧座外侧同时承受发动机输出最大扭矩T′，即

则

由式（18）、（19）、（21）得到以最大牵引力行驶时后驱动桥壳的合成弯曲扭矩M合′为

即

综上，以最大牵引力行驶时后驱动桥壳的弯曲扭矩应力δ弯′为

即

桥壳设计状态下的危险断面处的扭转弯曲截面系数W扭与式（14）一致，因此最大牵引力引起的扭转应力δ扭′为

即

则后驱动桥壳在危险断面处弯曲和扭转的合成应力为

即

计算结果表明，δ合′＜[δS]=400 N/mm2，由此判定汽车以最大牵引力行驶时后驱动桥壳的强度安全可靠。

3.5 后驱动桥半轴强度计算

此款皮卡车型的后驱动桥半轴为全浮式半轴，只承受扭矩，扭矩计算式为

即

M半轴扭=0.6 × 261Nm × 5.594 × 5.875=5147 Nm

当发动机输出最大扭矩时，半轴的扭转应力τ为

即

材料应力[τS]取值为490～588 N/mm2，τ＜[τS]，由此判定后驱动桥半轴的扭转强度安全可靠。

4 仿真分析

后驱动桥壳的材料参数见表2。

表2 材料参数

将表2 中各参数值输入仿真软件，轴管、桥壳、桥壳盖、桥壳加强板均采用壳单元进行模拟，焊缝处采用RBE2刚性单元进行模拟，轴管法兰盘及板簧座采用3D单元进行模拟。后驱动桥壳的模拟加载力如图7所示，其中，左右板簧座进行全自由度约束，在左、右轮心处各施加22 500 N载荷，方向垂直板簧座平面，并施加扭矩1 200 Nm，方向垂直鼓式制动器安装平面；后桥质心处施加3倍重力场，质心位置质量为120 kg。

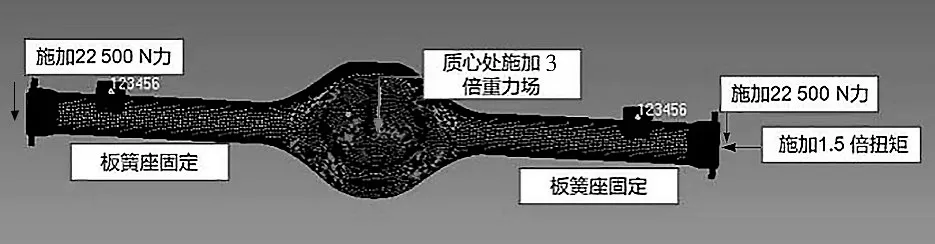
图7 模拟后驱动桥壳的施力点

后驱动桥的仿真分析结果如图8～12所示。

图8 为仿真模拟加载力的后驱动桥的整体位移分布，最大位移值为0.697 5 mm，小于设计要求（1.5 mm），满足设计强度要求。

图9 为仿真模拟加载力的后驱动桥的整体应力分布，最大应力位于板簧座附近，最大应力值为226 MPa，低于材料最小屈服强度（295 MPa），满足设计强度要求。

图9 后驱动桥整体应力分布

图10、11为仿真模拟加载力的后驱动桥桥壳上下片、桥壳盖和加强环的应力分布，其中最大应力值为112.2 MPa，低于材料屈服强度（295MPa），满足设计强度要求。

图10 后驱动桥桥壳上下片应力分布

图11 桥壳盖、加强环应力分布

图12为仿真模拟加载力后驱动桥法兰盘的应力分布，最大应力值为327.3 MPa，微高于材料屈服强度（315 MPa），将法兰材料调整为40#钢，其屈服强度为335 MPa，使材料满足设计要求。

图12 后桥法兰盘应力分布

5 耐久测试

5.1 桥壳测试

对后驱动桥壳进行垂直弯曲疲劳台架测试，共选取了3 个试验样件，其中2 个样件进行了8×105次疲劳测试后未出现裂纹，1 个样件进行了1.07×106次测试后出现桥管破坏现象，疲劳寿命标准要求大于等于8×105次测试，桥壳满足要求。

在桥壳垂直弯曲刚性测试中，满载轴荷时每米轮距桥壳垂直弯曲变形量为0.95 mm，未超过标准要求（1.5 mm）。

5.2 总成测试

对桥壳总成按照疲劳设计要求进行台架测试，测试进行53.7 万次时出现主齿断裂失效，标准要求最低疲劳寿命为30万次，总成满足要求。

5.3 整车测试

进行上述台架测试后，将此后驱动桥装车进行整车可靠耐久测试，试验过程中未出现桥壳开裂失效和漏油等问题。

6 结束语

本文针对非断开式后驱动桥进行强度计算校核，通过CAE仿真模拟，初步验证设计满足要求，为后期台架测试和整车可靠性测试提供数据参考。