线间距对600 km/h高速磁浮列车明线交会气动性能的影响

杨鹏，杨明智，张雷，赵凡，蔺童童，马江川

(1. 中南大学 交通运输工程学院 轨道交通安全教育部重点实验室，湖南 长沙，410075；2. 中国空气动力研究与发展中心 计算空气动力研究所，四川 绵阳，621000)

近年来，高速磁悬浮列车凭借非接触、无磨耗的技术特点和能耗低、爬坡能力强、噪声污染小的性能优势迅速发展[1]。然而，列车高运行速度也带来了诸多空气动力学问题，特别是当两列车等速交会时，列车头部或尾部经过另一列车瞬间会引起交会侧车身表面附近空气剧烈变化，产生强烈的瞬态冲击，严重时可能会造成车窗玻璃破碎、列车侧向摇晃以及轨道旁的设备疲劳损坏等问题[2]。线间距是影响列车气动特性的关键参数之一，增大线间距可以有效降低列车明线交会压力波。与列车低速运行不同，当列车运行速度达到600 km/h时，对应的马赫数为0.49，目前的线间距是否满足其交会需求尚未可知，增大线间距对列车气动性能产生的影响也亟待研究。

针对高速列车交会时的气动问题，FUJII 等[3]构建了用于模拟高速列车交会压力波特性的Fortified Solution Algorithm 方法，研究了列车交会压力波与气动力之间的作用关系；田红旗[4]提出了用于列车交会数值计算的非对称滑移网格技术，研究了列车运行速度、线间距、列车外形以及编组形式等参数对列车交会压力波的影响；梁习锋等[5]通过自研的瞬态压力测试系统对200 km/h动车组交会压力波进行了实车测试；李明水等[6]通过实车试验测量了高速磁悬浮列车5.1 m线间距下交会的压力载荷，为列车运行安全性评估提供了参考；杜健等[7-8]通过数值仿真研究了列车流线型长度及头部型线对其明线交会气动性能的影响，结果表明增大头部流线型长度及水平剖面型线斜率均可不同程度地减小列车交会压力波和侧向力；JOHNSON 等[9]采用动模型试验方法模拟了高速列车明线和隧道内交会时的气动特性，研究了运行速度、线间距和流线型长度对高速列车交会压力波的影响；魏洋波等[10-12]对高速轮轨列车明线或隧道内交会进行数值模拟，研究了不同线间距对列车交会压力波的影响，发现线间距减小会使列车明线以及隧道内交会的压力波增大；HUANG等[13]研究了两磁浮列车以430 km/h 的速度明线交会时产生的瞬态流场，分析了车身表面瞬态压力变化和轨道旁的列车风分布；王田天等[14]研究了不同隧道缓冲结构对列车隧道口微气压波的缓解作用；周细赛等[15-16]研究了不同头部主型线和不同编组长度的轮轨列车隧道内交会的气动特性，发现头部主型线和编组长度等因素对列车交会压力波和气动力有明显影响；MENG 等[17]采用重叠网格技术研究了流线型长度对列车明线交会时的气动特性影响，分析了列车交会时车身周围流场的流动情况和轨道旁的列车风变化。

目前，涉及600 km/h 高速磁浮列车交会的研究相对较少，在线间距对600 km/h 列车交会时的气动影响方面研究较少。本文作者结合列车动模型试验结果开展研究，通过三维、可压缩、非定常N-S方程和SSTk-ω湍流模型模拟2列3节编组的600 km/h 高速磁悬浮列车明线交会，探索了5.1、5.6 和6.1 m 线间距对车身周围流场、列车交会压力波以及列车侧向力等气动性能变化的影响规律，以期为高速磁浮列车的研制、磁浮线路的建设以及列车电磁力的调控提供参考。

1 数值模拟方法

1.1 计算模型

本研究选用的列车模型基于上海高速磁悬浮示范运营线列车，由头车、中间车和尾车3节编组组成。该列车模型全尺寸长度L为79.19 m，宽W为3.7 m，高H为4.1 m，最大横截面积为11.92 m2。C1、C2和C3分别表示列车的头车、中间车和尾车，图1所示为模型简图。磁悬浮列车底部采用T形导轨，轨道顶端距地面1.41 m。为了满足列车车身表面附面层y+在合理范围内，数值仿真模型采用1∶10的缩比。参考上海磁浮运营示范线5.1 m 线间距，本文所研究的线间距分别为5.1、5.6和6.1 m。

图1 磁悬浮列车模型Fig. 1 Model of maglev train

1.2 计算域和边界条件

采用重叠网格法模拟列车交会场景，计算区域简图见图2。该计算区域包含1 个静止的背景区域A 和2 个运动的重叠区域B、C，坐标系原点设置在重叠区域B内的Train1头车鼻尖位置，并以该车的运行方向为X正方向，计算区域长195.1H，宽35.4H，高19.5H，重叠区域长×宽×高为31.7H×1.39H×1.46H。为使2 列车流场不受彼此干扰并使初始流场稳定，两车鼻尖点初始距离为68.3H。在边界条件设置方面，车身表面、轨道以及地面设置为壁面，重叠区域表面边界类型为重叠网格，背景区域的四周及顶面设为自由流，流速设置为0。

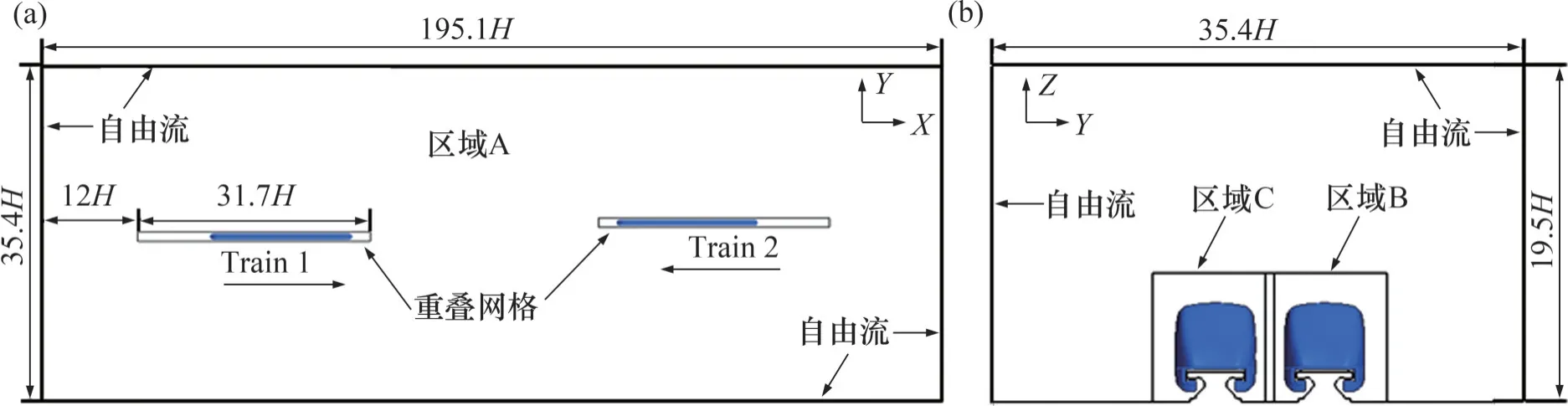
图2 计算区域及边界条件设置Fig. 2 Setting of calculation area and boundary condition

1.3 计算网格

在进行数值模拟时，通过CFD 软件STARCCM+对计算区域进行离散，网格类型选用切割体网格。为使车身周围流场变化过渡更加细致，在2 列车交会区域以及列车尾流区域进行了不同程度的网格加密，其中车身表面最小网格边长为0.003 0H，尾流加密区网格长度为0.024 4H，列车表面棱柱层数设置为15，增长率设为1.2。选用的模型网格数量约为7 784万个，重叠区域网格约占整体31.7%，保证了车身周围的网格密度。磁浮列车明线(5.1 m)交会运行网格分布见图3。

图3 磁浮列车明线(5.1 m)交会运行网格分布Fig. 3 Grid distributions of maglev train with open line(5.1 m) intersection operation

1.4 求解设置

数值仿真通过商用软件STAR-CCM+完成。为了阻止模型应力损耗及网格导致的分离，选择非定常SSTk-ω湍流模型的DDES方法模拟交会时的流场。600 km/h磁浮列车运行时速大于0.3Ma，因此，认为空气流动是可压缩的。时间采用较高精度的二阶隐式不定常格式，物理时间步长设为6×10-5s，每个时间步长设置20次迭代，保证了数值计算的残差和收敛性要求。为避免求解出现非正常物理量波动，列车采用先加速后匀速的启动方式，列车加速时间为0.12 s，总运行时间为0.24 s，列车运行稳定后的X向速度为±166.667 m/s，Y、Z向速度分量为0 m/s。对数据进行分析时，省去列车加速过程，仅保留列车稳定运行后的匀速交会过程。

2 数值方法验证

2.1 网格无关性验证

为验证网格密度对仿真结果的影响，在保证附面层总厚度不变的基础上，通过更改附面层内网格层数和流场局部加密尺寸设计了粗、中、细3种密度网格，网格具体尺度见表1。图4 所示为3种网格密度下的中车某点压力时程曲线。由图4可见：不同网格密度下的车身表面压力变化规律性良好，在峰值处存在一定差异，中网格和细网格最大幅值相对误差为2.7%，与粗网格相对误差为7.9%。综合考虑计算结果和计算资源，最终选择中等网格。

表1 网格无关性验证Table 1 Mesh independence verification

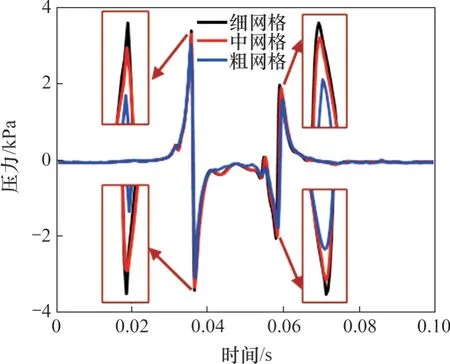
图4 不同网格密度下的中车某点压力时程变化曲线Fig. 4 Time history curves of pressure change at a certain point of middle car at different mesh densities

2.2 算法验证

为保证仿真结果的可靠性，通过对比动模型试验验证选用的数值模拟方法的正确性。动模型试验在中南大学轨道交通安全重点实验室进行，该试验线全长为164 m，试验线间距为5.1 m，试验车模型比例为1∶20，动模型高速磁浮列车模型如图5所示，列车速度选择为166.57 m/s 和166.55 m/s，满足本次试验要求[19]。图6所示为2种工况下交会侧车身中间截面某高度测点的压力时程曲线对比，表2 所示为该测点数值计算与动模型试验压力幅值，结果表明数值仿真与模型试验结果吻合良好，最大压力幅值相对误差均在4%以内，因此，可认为本文所采用的数值模拟方法可以准确模拟600 km/h高速磁悬浮列车明线交会。

图5 动模型高速磁浮列车模型Fig. 5 High-speed maglev trains of moving model test

图6 数值仿真与动模型试验结果对比Fig. 6 Comparisons between numerical simulation and moving model test

表2 压力波幅值数值模拟与动模型试验结果比较Table 2 Comparisons between numerical simulation of pressure wave amplitude and dynamic model test results Pa

3 结果分析

3.1 车身周围流场

从磁悬浮列车车身周围流场入手，通过瞬时涡结构、速度和压力分布云图等使列车交会时的流场可视化，分析5.6 m线间距下列车不同交会时刻的流场变化，进一步分析线间距变化对车身周围流场结构的影响。定义Train 1 头车鼻尖点所在位置截面为X=0、Z=0、Y=0。图7所示为列车明线交会过程示意图，文中t1为列车开始交会时刻(t1=0.150 0 s)，t3为列车头尾交会时刻(t3=0.173 7 s)，t5=0.197 5 s 为列车交会结束时刻，t2和t4分别为列车头部和尾部到达另一列车车身中间部位时的时间。

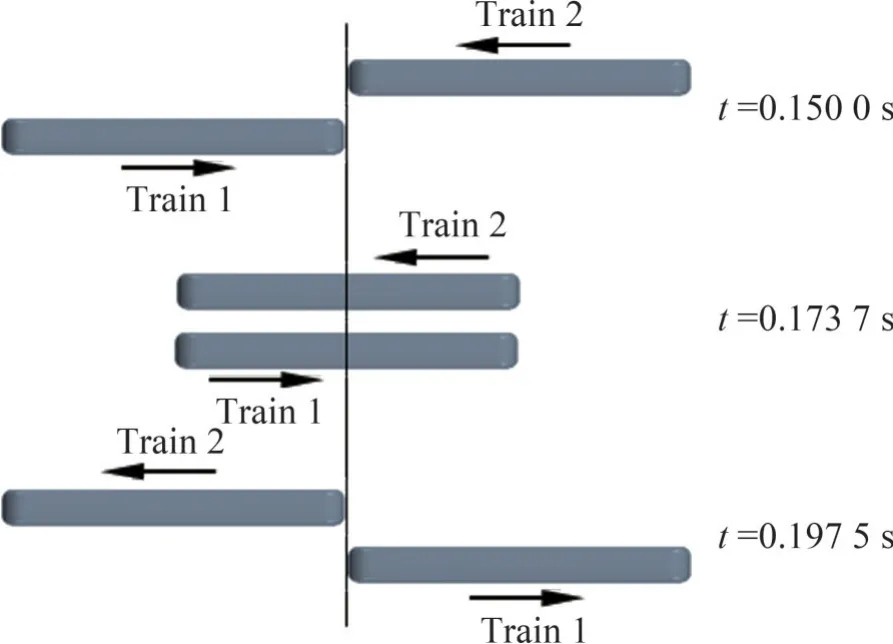
图7 列车交会时刻示意图Fig. 7 Schematic diagram of train passing each other time

为观察列车不同交会时刻的瞬时特征，以5.6 m 线间距为例，通过Q准则描述车身周围的瞬时涡结构。Q准则是一种计算效率高、效果显著的涡识别方法，被广泛应用于涡结构识别和提取[17-18]。图8所示为两车以600 km/h速度交会时的俯视图，Q取为20 000，U=V/166.667，其中，U为量纲一的速度系数，V为流场中某点的速度。由图8可见：列车运行时尾车下游会形成2条方向相反的紊乱漩涡流，列车尾迹区存在大量不同特征尺度的涡结构，且涡强度随距尾车距离增大而减小，头车和中间车附近则无此特征；列车头尾交会后，受另一列车尾涡影响，交会侧车身周围流场湍流强度增加，并且易产生交变载荷，导致车体表面和轨旁设备出现疲劳强度破坏；列车交会结束后，交会区域流场受两列车尾涡相互影响，出现大量紊乱、小尺度漩涡结构，使得流场流动更加无序。

图8 不同交会时刻下的Q准则瞬时等值面图Fig. 8 Instantaneous Q-criterion iso surface maps at different intersection moments

为进一步观察列车交会时车身周围流场结构，分析了列车在5.6 m线间距下交会时的流场分布特征。列车开始交会时不同高度截面的速度流场如图9 所示(其中，U为速度系数)。由图9 可知：受另一列车来流影响，开始交会时两交会侧车身流场之间出现明显的低速区域，随高度增加，该低速区域逐渐减小，车身左、右两侧流场速度分布对称性增强。图10 所示为不同交会时刻下头车周围Z=0 截面的流场。由图10 可知：交会时另一列车交会侧车身受列车头车影响导致其车身周围流场速度比非交会侧车身周围流场速度大，头尾交会后，交会侧车身受另一列车尾流影响流场速度分布较为杂乱，车身左、右两侧流场速度分布对称性较差，列车尾流影响区域长度在1 倍车长以上。

图9 开始交会时不同高度截面的速度流场Fig. 9 Velocity flow field of different height sections at beginning of train intersection

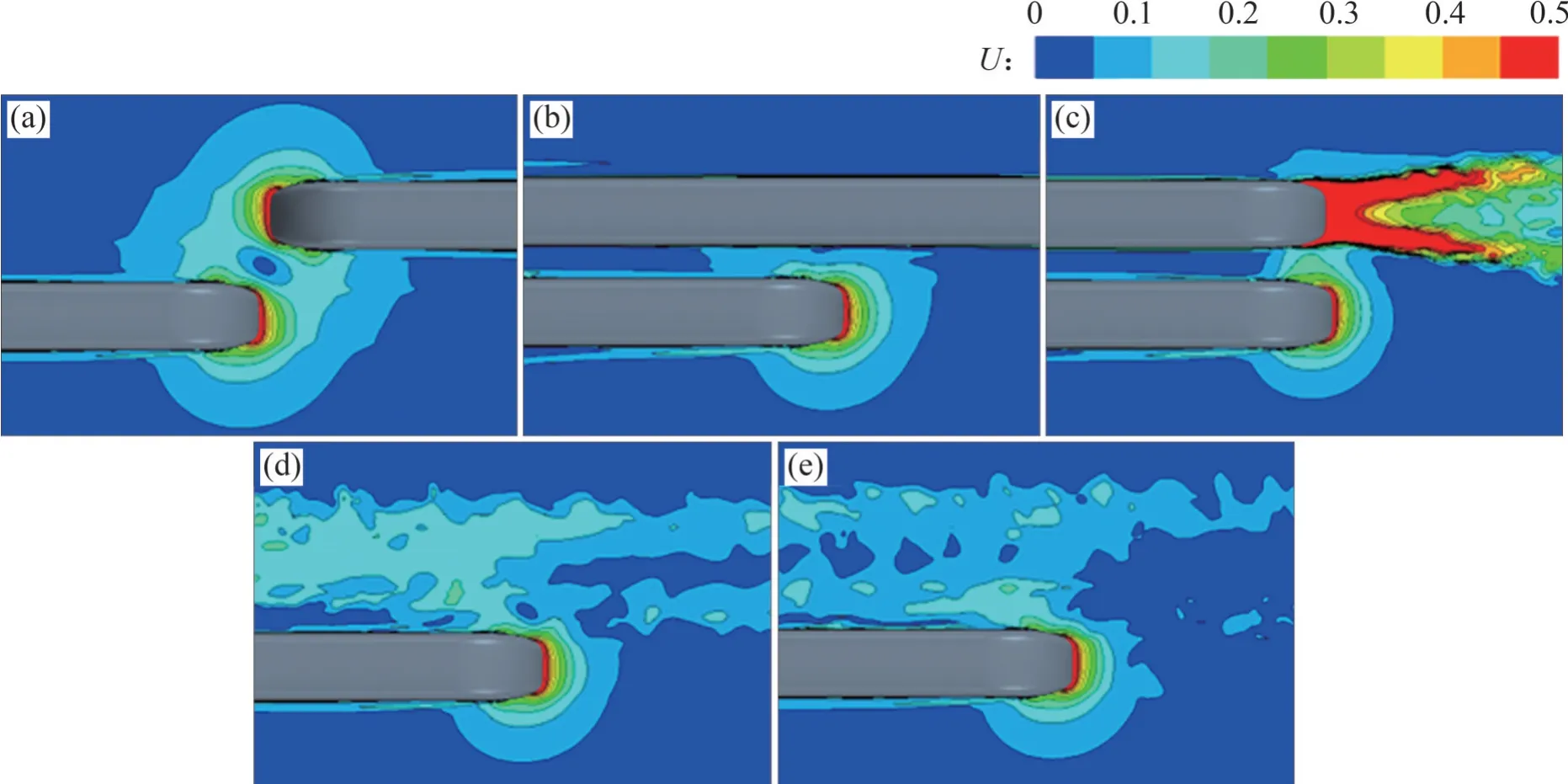
图10 不同交会时刻Z=0截面的头车速度流场Fig. 10 Velocity flow field of Z=0 section at different intersection time of head car

图11 所示为不同线间距下列车交会结束时Train1 列车尾后2H处的流线图。由图11 可见：相比于非交会侧，交会侧尾后流场受另一列车壁面影响导致气体自由流动被限制，车身之间的流场漩涡结构相对密集，随线间距增大，该处的漩涡长度也逐渐增大。3种线间距下形成的角度分别为α、β和γ。当线间距增大时，涡漩展向角度逐渐增大，流场流线更为稀疏，因此，可认为增大线间距可减弱列车尾涡对另一列车交会侧车身周围流场的影响。

图11 不同线间距下列车交会结束时尾后2H处流场流线Fig. 11 Streamline of flow field at 2H behind tail car at the end of train intersection with different line spacings

车身周围流场作用强度以速度和压力表征。图12 所示为列车开始交会时Z=0 截面的头车速度流场。由图12 可见：不同线间距下列车头车周围流场的速度分布特征类似，随线间距增大，两交会侧车身之间的低速区域逐渐扩大，车身左、右流场速度分布呈对称性增加。图13 所示为不同线间距下列车交会开始时的压力流场。由图13可知：3种线间距下列车交会时头车周围的流场压力分布规律一致，车身周围流场压力随距列车壁面距离增大而减小；随线间距增大，两交会侧车身之间流场的压力逐渐减小，非交会侧车身周围流场所受影响较小。

图12 不同线间距下列车开始交会时的速度流场Fig. 10 Velocity flow field of trains at the beginning of intersection with different line spacings

3.2 列车交会压力波

为便于分析线间距增大对列车交会压力波的影响，以5.1 m 线间距为例分析列车交会压力波。选取Train 1 头车(C1)、中间车(C2)、尾车(C3)及两节车中间部位(C12、C23)，其不同情况的交会压力波时程变化曲线如图14 所示，图中，位置后面的数字表示测点编号。由图14 可知：在同一高度不同截面交会侧，列车交会压力波头波先出现正波后迅速变为负波，最大正波极值约出现在中间车中间截面位置，尾波先出现负波又迅速变为正波，其幅值皆比头波的幅值小；中间车(C2)交会侧车身中间截面不同高度测点的变化规律基本上与前面的情况一致，交会压力波幅值自列车顶部至底部先增大后减小，底部幅值仍远比顶部的幅值大，最大幅值出现在鼻尖点高度附近；对于中间车(C2)同一截面高度交会侧与非交会侧，列车交会过程中车身两侧压力波动变化区别明显，交会侧车身压力变化远比非交会侧的大。

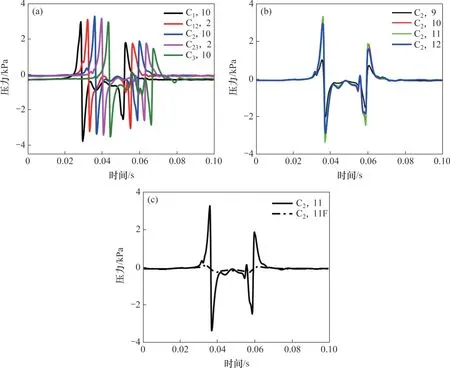
图14 5.1 m线间距下列车表面测点压力变化时程曲线Fig. 14 Time history curve of pressure change at measuring points on train surface with line spacing of 5.1 m

为探明600 km/h 磁悬浮列车明线交会与低速的不同，以5.1 m 线间距下时速350、430、500、550 和600 km 磁浮列车交会为例，图15 所示为不同运行速度下列车等速交会时中间车中间截面在同一高度测点的压力幅值。从图15 可以看出：当磁浮列车明线交会时，列车表面测点压力变化幅值与车速的二次方近似呈正比。

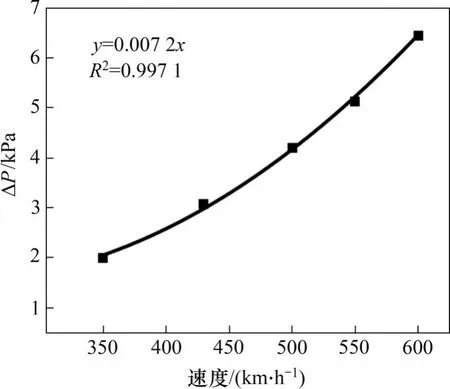
图15 5.1 m线间距下不同运行速度列车同一测点压力幅值Fig. 15 Pressure amplitude at the same measuring point of trains with different running speeds with line spacing of 5.1 m

图16 5.1 m线间距下列车不同交会时刻车身表面压力分布Fig. 16 Pressure distribution on train body surface at different intersection times with line spacing of 5.1 m

为便于分析，对列车压力系数做出如下定义：

式中：Cp为压力系数；P为流场某处的压力；ρ为空气密度，取1.225 kg/m3；v为列车运行速度，取166.667 m/s。

图16所示为5.1 m线间距下Train 1列车不同交会时刻的车身表面压力分布，其中，H和T分别指列车头车和尾车。由图16 可知：对于Y=0 截面，列车头尾部鼻尖点处为较强的正压，且头部压力大于尾部压力，头、尾车流线型与非流线型过渡区域为较大的负压区，直线段车身表面压力较为稳定；列车交会过程中车身表面压力受另一列车表面压力影响出现正、负波动。对于Z=0截面，列车交会过程中交会侧车身表面压力分布受影响较大，车身表面压力波动远比非交会侧的波动大；列车开始交会时车身表面出现最大正压，分布在头车交会车身侧流线型与非流线型过渡区域，头尾交会时车身表面出现最大负压，分布在头车交会侧车身直线段上游区域。根据以上分析，列车交会过程中车身表面压力分布与上述交会压力波变化和压力流场分布特征一致。

以交会压力波幅值描述交会压力波动程度，根据以上分析，以交会侧车身中间截面11 号测点为例，图17所示为不同线间距下的列车交会压力波变化时程曲线。由图17可知：5.1 m线间距幅值及正、负压力波峰值分别为6 539、3 298和-3 241 Pa，增大至5.6 m 线间距时，其幅值及正、负压力波峰值为4 694、2 245 和-2 449 Pa，分别减小28.2%、31.9%和24.4%；当线间距增大至6.1 m时，其幅值及正、负压力波峰值分别为3 765、1 804和-1 960 Pa，分别减小42.4%、45.3%和39.5%，压力波尾波缓解作用相对头波而言较小。因此，增大线间距可以有效缓解列车交会压力波，且对正波缓解作用比负波缓解作用大，头波缓解作用比尾波缓解作用大。

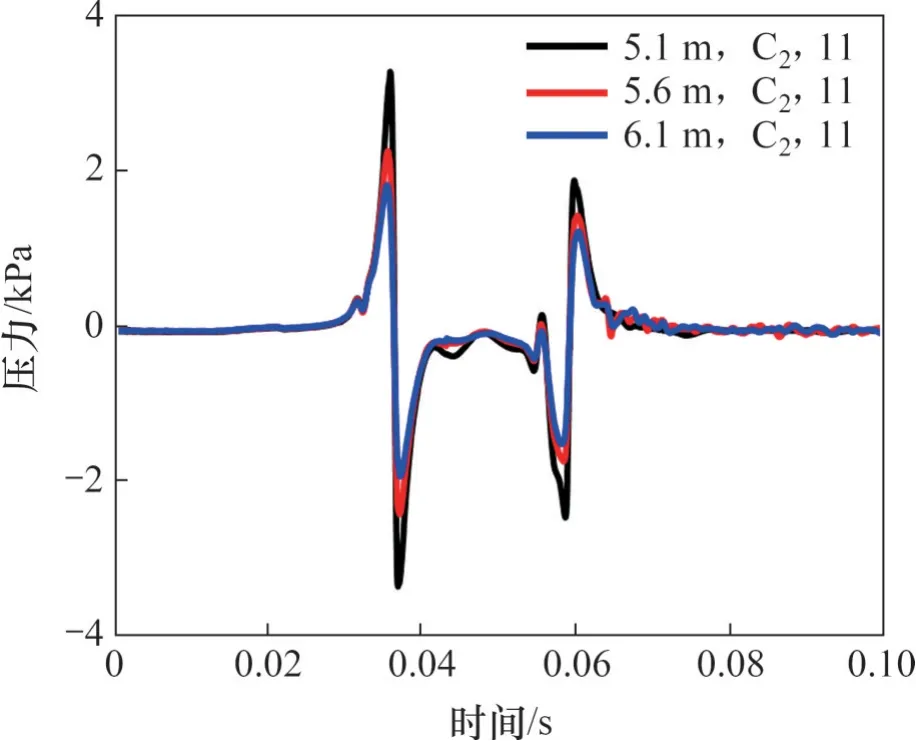
图17 不同线间距下中车中间截面交会侧测点压力变化时程曲线Fig. 17 Time history curves of pressure change at measuring points on intersection side of intermediate section of intermediate vehicle with different line spacings

3.3 列车侧向力

列车交会过程中的侧向力是影响其交会安全性的重要参数，为便于分析，对列车侧向力系数进行如下定义：

式中：Cy为侧向力系数；Fy为侧向力；S为列车横截面正投影面积，取11.915 m2。

以侧向力负值表示列车受到外推、正值表示列车受到内拉作用，图18 所示为不同线间距下列车头车、中间车和尾车侧向力变化时程曲线。由图18 可知：列车在交会过程中各节车分别受到两次侧向力交互推拉作用，在侧向力交互推拉时会对电磁导向系统和列车横向阻尼形成瞬态冲击，引起列车导向间隙出现变化，严重时甚至导致列车产生横向摆动。增大线间距会对列车侧向力产生缓解作用。不同线间距下列车交会过程中的各节车侧向力系数见表3，其中Rmax为侧向力系数最大值，Rmin为侧向力系数最小值，Δ为侧向力系数幅值。

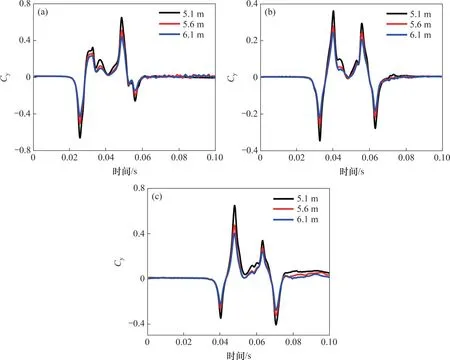
图18 不同线间距下列车明线交会时侧向力系数时程曲线Fig. 18 Time history curves of yawing force coefficient of open line intersection of trains with different line spacings

表3 不同线间距下列车交会时的各节车侧向力系数Table 3 Yawing force coefficient of each car when trains meet with different line spacings

由表3可见：列车头车侧向力系数幅值比中间车和尾车的大，尾车的幅值比中间车的大，其中头车侧向力系数幅值约为中间车的2倍，因此，列车交会过程中头车受侧向力影响最大，摇摆风险最大；当线间距由5.1 m 增大至5.6 m 时，列车头车、中间车及尾车侧向力幅值分别减小22.9%、24.7%和24.6%；当列车头车、中间车及尾车侧向力幅值继续增大至6.1 m 时，其幅值分别减小33.8%、34.1%和35.7%。因此，增大线间距对尾车侧向力幅值的减缓作用最大，中间车次之，头车最小，并且随线间距的增大，侧向力的缓解作用逐渐减小。

4 结论

1) 不同线间距下的车身周围流场分布特征类似。在列车交会过程中，交会侧车身受另一列车头车和尾流影响导致其周围流场压力和速度比非交会侧的大。随线间距的增大，列车尾涡展向角逐渐增大，车身两侧流场分布特征对称性增加，交会侧车身之间流场的速度和压力减小。

2) 增大线间距可以减小列车交会压力波，且对交会压力波头波的减缓效果比对尾波的好，正波的减缓效果比负波的效果好。不同线间距下的列车交会压力波变化规律基本一致，压力波幅值与列车运行速度的二次方近似呈正比，且随线间距增大而减小。当线间距由5.1 m增大至5.6 m时，列车交会压力波正、负峰值及幅值可分别减小31.9%、24.4%和28.2%；继续增大至6.1 m，缓解效果减弱，其正、负压力波峰值及幅值分别减小45.3%、39.5%和42.4%。

3) 列车侧向力幅值的减小效果随线间距增大而减弱。列车各节车的侧向力幅值均随线间距增大而减小。在交会过程中，头车侧向力幅值比尾车和中间车的幅值大，但增大线间距对尾车侧向力减缓效果比头车和中间车的减缓效果好。当线间距由5.1 m 增大至6.1 m 时，列车头车、中间车和尾车侧向力幅值分别减小33.8%、34.1% 和35.7%。