离心载荷对轴类部件过盈配合的影响研究
舒易亮,刘志明,杨广雪,高敬宇,刁晓明
(1. 北京交通大学 机械与电子控制工程学院,北京,100044;2. 中国铁道科学研究院集团有限公司 机车车辆研究所,北京,100081)
过盈量是保证轴类过盈配合结构传递扭矩和载荷的重要参数,在工程结构件正常工作时,过盈量将直接影响结构的过盈配合性能。大多数工程机械紧固连接配合通过压装法或温差法实现过盈装配。然而,轴类过盈配合部件往往服役于高转速环境,如铁路机车轮轴[1]、高速旋转主轴与转子或轴承[2-4]、齿轮与轴[5]、涡轮发动机转子[6]等。高速旋转的轴类过盈配合部件在离心载荷的作用下,过盈配合的2 个部件在接触面产生径向位移差,从而导致旋转部件过盈量减小[7-9]。而轴类过盈配合部件是通过过盈连接传递扭矩及轴向载荷的,当过盈量减小到机械设计允许的最小过盈量[10]时,将直接导致轴类过盈配合部件的性能失效。
国内外学者采用有限元方法对轴类过盈配合结构接触面间的应力、位移,接触压应力及过盈量等参量的变化规律进行了大量的研究。ZHAO[11]通过有限元方法对实心和空心滚子轴承进行了多体接触分析,研究了载荷在滚动轴承内部的分布规律。ZHANG 等[12]基于有限元方法对环形齿轮-轮毂过盈连接部件开展仿真研究,得到了比传统Lame 方程更加完整、更加精确的过盈配合部位的应力。张松等[2]采用有限元方法对高速旋转主轴的过盈连接特性进行了研究,发现主轴与转子间的过盈连接特性与初始过盈量和旋转角速度有关。当主轴转速高于松脱速度时,主轴与转子间处于分离状态,两者之间的接触应力和扭矩下降为零。单宝峰等[13]对影响高速主轴与轴承之间过盈量的因素展开了分析,指出影响主轴轴承过盈量的因素主要有温度、离心力及初始配合过盈量等。
由于过盈量是影响轴类过盈配合部件连接性能的一个关键参数,当轴类过盈配合部件承受周期性的旋转弯曲载荷时,靠近接触边缘的局部接触区域就会产生周期性的往复滑移,从而引起微动疲劳损伤[14]。杨广雪等[15]指出,接触压力、微动滑移幅值、摩擦剪切应力等参数是影响微动疲劳损伤的重要参数,在离心载荷作用下,高速列车轮轴过盈量的变化将直接导致过盈配合面的微动损伤参量发生变化。ZHANG等[16-18]基于旋转弯曲微动疲劳试验和微动疲劳定量仿真模型,研究了过盈配合试样的微动疲劳损伤,揭示了微动疲劳裂纹的表面形貌演化、磨损特征及损伤分布变化特征。ZENG等[19]提出了一种全尺寸过盈配合轮轴裂纹萌生的有限元预测模型,考虑了微动磨损引起的应力重分布对微动疲劳的影响,并提出了缓解轮轴过盈配合接触边缘部位应力集中的方法。陈刚等[20-24]开展了列车车轴过盈配合部位的微动疲劳试样或者全尺寸实物轮轴的微动疲劳试验及仿真研究,指出轮轴配合过盈量作为一个关键参量时刻影响车轴的微动疲劳的损伤。然而,实际轮轴过盈量在不同加载循环次数下的变化情况以及过盈量沿配合区域的轴向分布特征不能观测到,而且现有的研究并没有考虑过盈量在不同旋转角速度下的减小效应对车轴微动疲劳的影响。因此,研究轴类过盈配合部件过盈量在不同离心力载荷作用下的减小效应,同时考虑初始过盈量和离心载荷的影响,建立过盈量随角速度变化的定量分析公式模型是非常有必要的。
轴类部件过盈配合接触仿真研究是属于高度非线性的复杂问题,配合面间呈现复杂的接触状态和应力状态。随旋转角速度增大,离心载荷增大,将导致轴类过盈配合部件的过盈量的减小效应逐渐增强,甚至可能引起轴类过盈配合部件的性能失效。孙林平等[8]对离心载荷作用下实心简化轮轴的过盈量的变化进行了有限元仿真分析,并结合有限元仿真结果分析研究了接触压应力的变化规律,指出在离心载荷对轮轴过盈配合有重要影响,当转速达到一定量级时,会出现轮轴分离现象。庞强宏等[9]采用Ansys Workbench 软件分析了圆盘-轴和齿轮-轴在离心力和高温同时作用下的接触应力和等效应力分布规律,综合考虑过盈连接件可能面临的复杂工况,使设计的过盈配合结构性能更加可靠。卢萍等[7]仿真分析了列车轮轴在高速运行情况下的轮轴连接性能,指出离心载荷会降低轮毂孔面的接触压力。然而,研究者仅仅对轴类过盈配合部件在离心力载荷作用下过盈量的减小效应进行了研究,推导公式时未考虑初始过盈量的影响,也未将仿真分析结果和理论计算结果进行详细对比,更未分析离心载荷作用下轮轴过盈量的定量变化规律和特征。
本文作者将离心载荷对轴类过盈配合部件连接性能的影响研究简化成平面应力问题,推导含初始过盈量的轴类过盈配合部件在不同旋转角速度下的过盈量变化公式。考虑初始过盈量的影响,定量地分析研究离心载荷对轴类过盈配合部件过盈量的影响。基于简化的轮轴实物等效模型,将推导的理论公式进行数值模拟,结合有限元仿真分析轴类过盈配合部件在不同旋转角速度下的过盈量及接触压应力的变化特征,以验证所推导理论公式的准确性。
1 轮轴过盈配合计算方法
1.1 过盈配合接触压力
轮轴过盈配合仿真计算属于接触非线性问题,传统设计方法以厚壁圆筒为模型,采用弹性力学的方法计算过盈连接所需要的过盈量,保证在合理的过盈量下能传递扭矩和轴向力。一般可将轴类过盈配合部件看作组合厚壁圆筒,进而分析厚壁圆筒过盈面间变形和应力的关系。如图1 所示。假设组合圆筒中的内圆筒的内半径为R1,共同配合半径为R2,外圆筒的外半径为R3,过盈配合的长度无限长,不考虑轴向的边界条件,组合圆筒的半径过盈量为δ,内、外圆筒的弹性模量分别为E1和E2,泊松比分别为υ1和υ2。根据过盈量δ和轮轴配合前、后的变形协调条件,轮轴过盈配合的接触应力P可由Lame方程[25]求出:

图1 组合厚壁圆筒简图Fig. 1 Sketches of combined thick-walled cylinder
若轮轴材料属性相同时,则轮轴弹性模量E=E1=E2,泊松比υ=υ1=υ2,接触应力P可进一步简化为
当内圆筒为实心轴时(即R1=0时),接触应力P可进一步简化为
然而,在实际工程问题中,轴类过盈配合部件的轮轴的材料往往不一致,材料力学性能也各有差异。为准确获得轮轴在初始过盈量下的接触压应力,有必要采用式(1)进行精确计算。若轴类过盈配合部件的轮轴的材料一致或者属性相近,可采用式(2)进行计算,也可以得到接近实际的应力。
1.2 离心载荷下过盈量的减小效应
如图1所示,若2个装配的圆柱体处于含初始过盈量的接触状态,则在高速旋转离心载荷作用下,内圆筒和外圆筒将出现径向位移。对于轴类过盈配合部件,轴的长度远比轮的厚度大,当轮轴结构在高速旋转时,可以简化成含初始接触压应力的2个等厚旋转圆盘。对于任意的等厚旋转圆盘,密度为ρ,若以均匀角速度ω旋转,则圆盘内半径为r的单位圆柱的离心力Fd大小相同,方向沿着各自的径向方向,且与φ无关,可以看作轴对称问题[26],如图2 所示。图2 中,u为微小单元的径向位移,r为微小单元相对圆心位置的半径,φ为力的夹角,σφ为旋转角为φ时的应力,σr为径向应力。

图2 等厚旋转圆盘受力示意图Fig. 2 Schematic diagrams of force of rotating disc of equal thickness



2 轮轴等效模型建立及数值模拟
2.1 实物轮轴模型参数
高速列车轮轴往往依据普速既有列车轮轴的设计经验选择轮轴过盈配合量,标准TB/T 1718.3—2018[27]中规定动车组轮轴间的过盈量为0.10%dm~0.15%dm+0.06 mm(dm为车轴轮座直径),故将轮轴间的半径过盈量取为0.15 mm,接近过盈量的中间值。真实车轴轮座区域的直径为200 mm,轴身直径为173 mm,车轴轮座直径与轴身直径之比为1.156。空心车轴内孔直径为30 mm,车轴轮座区域左右两侧的突悬量分别为1.635 mm 和3.5 mm,两侧端部过渡圆弧弧长分别为25 mm 和16 mm,卸荷槽半径和深度分别为16 mm和1 mm,实物轮轴模型如图3所示。考虑到模型的对称性,选取高速列车实物轮轴模型的1/4模型,通过有限元仿真软件计算不同初始过盈量下接触压应力在车轴轮座区域的轴向分布,为了获得接触边缘区域的精确应力,在接触边缘区域进行局部细化网格,采用有限元数值求解进行网格划分的最小单元长度和宽度均为400 μm[28],有限元网格模型如图4 所示,仿真计算时在对称面施加对称边界条件。

图4 轮轴1/4对称有限元网格模型Fig. 4 Symmetric finite element mesh model of 1/4 wheel axle
2.2 轮轴等效模型建立及仿真方法
采用有限元软件计算轮轴实物1/4模型在不同过盈量下的接触压应力沿轴向相对位置的分布特征,如图5 所示,轴向正方向定义为有A端指向B端,并以A端为横坐标零点位置。由图5可知:轮轴过盈配合区域的接触压应力与过盈量呈线性正相关关系,相同过盈量下分布呈现中部平缓、数值小,接触边缘应力急剧增大的特征,与文献[15]中试样轴过盈配合部件的接触压应力分布特征一致。实物轮轴过盈配合区域接触边缘左侧的接触压应力比右侧边缘的接触压应力小,这是因为车轴轮座区域左侧突悬量比右侧突悬量小,且左侧过渡圆弧比右侧过渡圆弧大。车轴轮座区的微动疲劳损伤与接触区域的接触压应力、相对滑移幅值及外界振动载荷密切相关,而车轴轮座区内侧边缘的接触压应力远比轮座区外侧边缘的接触应力大,故从接触压应力角度看,车轴轮座区域内侧比车轴轮座区域外侧更容易出现微动疲劳损伤[28]。

图5 不同过盈量下接触压应力沿轴向分布Fig. 5 Distributions of contact compressive stress along axial direction with different interferences
将实物轮轴简化成等效轮轴模型,通过式(1)结合仿真结果中车轴轮座中间区域的接触压应力数据,取平均得到的等效接触压应力Pave,进而求解出车轮的等效外径R3。考虑到轮轴过盈配合中间区域的接触压应力与Lame方程的压应力计算值较接近[29],故选取过盈量为150 μm、轴向相对位置为60~120 mm 的模型有限元节点的接触压应力进行求解,如下式所示:
由于轮轴材料弹性模量相差不大,为了计算方便,可认为轮轴弹性模量相等。取E=E1,υ=υ1,R1和R2分别参考图3 中图4 中轮轴1/4 对称有限元网格模型实物轮轴参数,分别取值为15 mm 和100 mm。根据式(2)可计算车轮的等效外径R3,如式(21)所示,同时考虑到建模方便,将计算得到的R3向上取整为230 mm。
为验证车轮等效外径的准确性,基于式(1)分别计算过盈量分别为100、115、130、150、180和210 μm 时的接触压应力,与仿真求解车轴轮座中间区域的节点接触压应力平均值进行对比,如表1所示,实物轮轴过盈配合中间区域的有限元求解节点平均值与采用等效车轮外径基于式(1)计算的结果相对误差均小于1%,证实了车轮等效外径R3计算结果的合理性。

表1 不同过盈量下仿真平均值与Lame公式计算值比较Table 1 Comparisons of simulation average value and Lame formula calculation value with different interferences
基于高速列车实物轮轴模型过盈配合区域的尺寸参数及求解的车轮等效外径R3,通过有限元前处理软件Hypermesh进行几何前处理建模,建立轮轴过盈配合等效模型。轴部件的内径R1为15 mm,轮部件的外径R3为230 mm,轮轴共同接触区域的半径R2为100 mm,模型参数如图6所示。轮轴过盈配合部件的轴的弹性模量为E1为2.05×105MPa,泊松比为υ1为0.3,轮的弹性模量E2为2.1×105MPa,泊松比为υ2为0.3。采用1/4 轴对称模型进行仿真分析,同时为了在接触区域获得精确的有限元仿真结果,采用精细化网格技术,在接触区域的单元长度为ESmin为1 mm。

图6 轮轴等效有限元模型Fig. 6 Equivalent finite element model of wheel and axle
在轮轴过盈配合部件的轮轴间建立接触对,轴的接触面为接触从面,轮的接触面为接触主面,法向接触行为采用硬接触模拟,主从面节点保证一一对应,接触面间的摩擦因数取0.6,切向行为采用罚函数接触算法模拟,轮轴过盈配合部件的主从面间的过盈量取为0.15 mm。仿真求解在ANSYS软件中求解,共分为2个载荷步:第1个载荷步施加初始过盈量CONF为0.15 mm,同时为避免轮轴主从接触面节点存在初始的间隙,设定初始间隙调整量为0.001 mm,时间步长为2 s;第2 个载荷步施加全局的旋转角速度0~1 207.73 rad/s,时间步长为20 s,表示在20 s时间内,旋转角速度由0 rad/s线性增大到1 207.73 rad/s。
2.3 数值模拟分析
根据前文对离心载荷下过盈配合轮轴过盈量的变化理论公式推导结果,在MATLAB 进行数值模拟仿真。理论计算的过盈接触压应力、轴的径向位移(uaxle)和轮的径向位移(uwheel)及轮轴接触径向位移差随旋转角速度的变化如图7所示。由图7可知:当初始过盈量0.15 mm 时,接触压应力为124.62 MPa,随旋转角速度增大,接触应力不断减小,当旋转角速度增至966 rad/s 时,接触压应力减小至0 MPa。

图7 理论仿真接触参数随旋转角速度的变化Fig. 7 Theoretical simulation of contact parameters as a function of rotational angular velocity
由含初始过盈的轮轴理论公式可知,轴部件外侧接触面和轮部件内侧接触面在径向方向会发生相对位移,其相对径向位移之差与过盈量相同。在离心载荷作用下,轴外表面和轮内表面的径向位移及接触过盈量的变化如图7 所示。从图7 可见:对于初始过盈量为0.15 mm的轮轴部件,当轴部件外侧接触面的径向过盈位移为-0.05 mm,轮部件内表面的径向过盈位移为0.10 mm。旋转角速度小于966 rad/s 时,轮轴接触面的径向过盈位移和接触过盈随旋转角速度增加不断减小,呈非线性特征;当旋转角速度等于966 rad/s 时,轴部件和轮部件的径向过盈位移及接触过盈位移均变为0 mm,接触压应力减小为0 MPa,表明此时轮轴过盈配合刚好由过盈配合状态转变为间隙配合状态,随旋转角速度继续增大,轮轴接触间的间隙不断增大,间隙配合状态时的轮轴间隙的增长速率比过盈配合状态的轮轴过盈量的减小速率大,这是由于在过盈配合状态时,轮轴间存在相互作用约束,而在间隙配合状态时,轮轴接触面相互分开,轮轴间不再存在相互作用。
3 有限元仿真分析
3.1 含初始过盈量的接触压应力仿真
采用有限元软件ANAYS对含初始过盈量下轮轴间接触压应力进行仿真分析,对1/4轮轴等效模型施加平面对称约束,之后施加过盈量0.15 mm。由式(1)可计算出过盈配合轮轴的在初始过盈量下的接触压应力理论值约为124.62 MPa。含初始过盈量的接触压应力有限元仿真结果云图如图8 所示,仿真的过盈接触压应力沿轴向分布特征和公式理论计算结果比较如图9 所示。由图8 和图9 可以看出:理论公式计算的接触压应力与仿真结果近似相等,且在接触边界处偏差较大,这是因为有限元仿真在接触边界存在一定的应力集中,故可以认为有限元仿真的结果与理论值比较吻合。
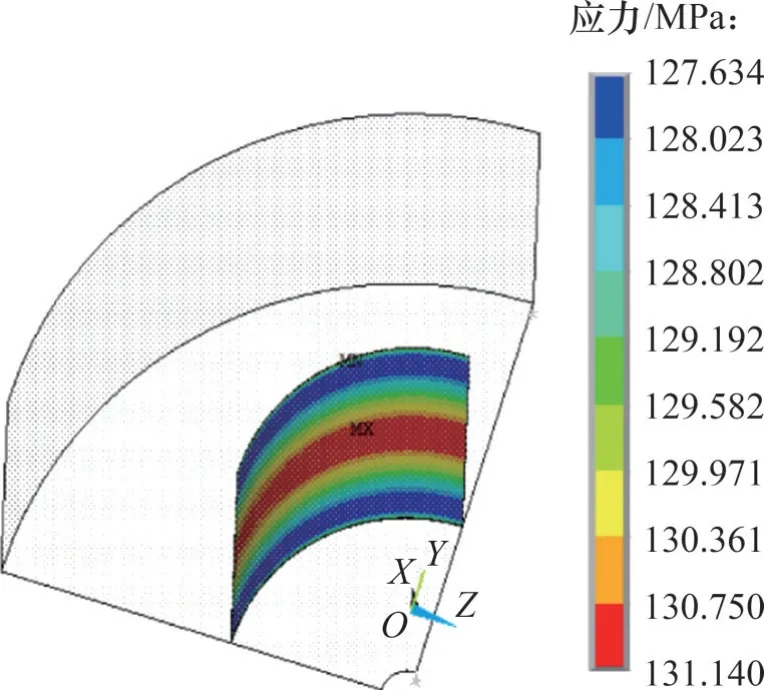
图8 过盈接触压应力仿真结果Fig. 8 Simulation results of interference contact pressure stress

图9 过盈接触压应力沿轴向分布Fig. 9 Distributions of compressive stress of interference contact along axial direction
3.2 离心载荷下的过盈量仿真
采用ANAYS有限元软件对离心载荷作用下轮轴过盈量的减少量进行仿真分析,旋转角速度ω的取值范围为0~1 207.73 rad/s,并在仿真时间步20 s内呈线性增大。选取轮轴轴向位置中间处的节点作为研究过盈接触参数的对象,ANSYS 中接触参数随旋转角速度的变化如图10 所示,其中uaxle、uwheel及Δuaxle_wheel分别为轴的径向位移、轮的径向位移及轮轴径向位移差。初始接触压应力和初始过盈量分别为131.14 MPa和0.15 mm,且接触压应力及基础过盈量随角速度增大而减小,呈现非线性特征。当旋转角速度为953 rad/s 时,接触压应力减小至0 MPa,此时,过盈量减小至0 mm。若角速度继续增大,则轮轴配合由过盈配合状态转变为间隙配合状态,与MATLAB 中的理论数值模拟结果基本一致。
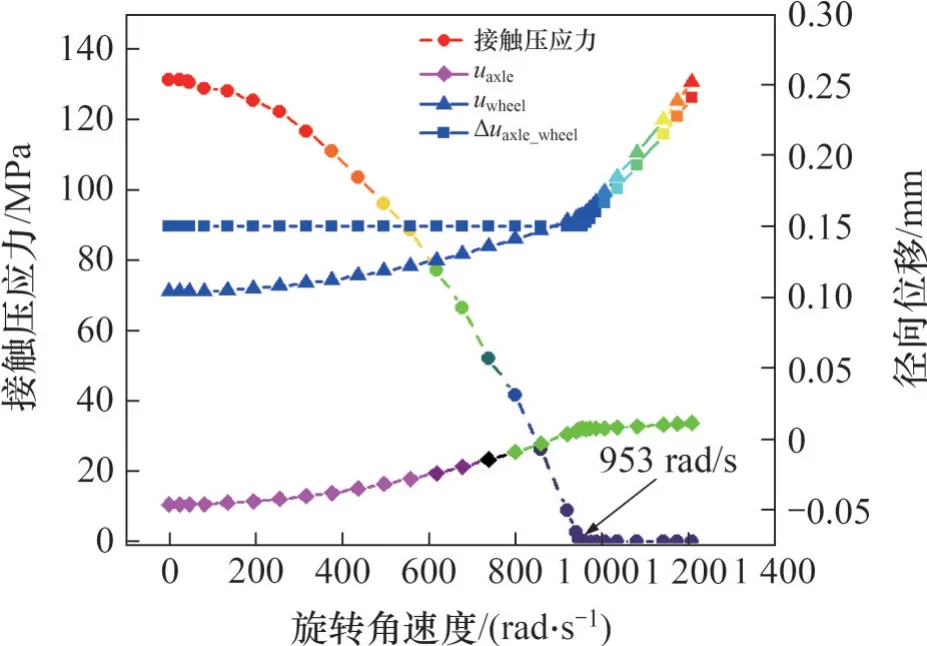
图10 仿真接触参数随旋转角速度的变化Fig. 10 Changes of simulated contact parameters with rotational angular velocity
ANSYS 仿真计算的过盈量在旋转角速度处于0~953 rad/s变化期间,轮轴接触面的径向位移差一直为0.15 mm,数值上与过盈量相等,这与MATLAB 中数值模拟过盈量随角速度增大而减小的现象有所不同。这是因为在ANSYS有限元软件中,含初始过盈量的过盈配合是基于有限元软件算法通过轮轴接触面的径向位移施加实现的,所以,当施加初始过盈量时,轮的径向位移为-0.05 mm,轴的径向位移为0.10 mm。在旋转角速度从0 rad/s增大到953 rad/s时,轮轴的径向位移呈非线性同步增加。但是,径向位移差一直保持为0.15 mm 不变,在此过程中轮轴处于过盈配合状态。接触面的位置是轮轴过盈配合面的共同接触面处,轴部件的外表面和轮部件的内表面一直处于接触状态,并未发生分离。故此阶段的相对位移差一直与初始过盈量的状态一致。当角速度大于953 rad/s 时,轮轴过盈配合由过盈配合状态转变为间隙配合状态,轮轴径向位移差将继续增大,增长斜率基本和轮的内表面径向位移增长斜率基本一致。
3.3 有限元分析与理论模拟对比
含初始过盈量的轮轴过盈配合部件在离心力载荷作用下的接触压应力变化,如图11 所示。由图11 可知:随旋转角速度增大,理论数值模拟和有限元仿真计算得到的接触压应力随旋转角速度的变化曲线基本一致,都呈现非线性特征。理论数值模拟及有限元仿真计算的径向位移差变化曲线如图12 所示。为了将理论数值模拟和有限元仿真计算的过盈量变化结果进行对比,将理论数值模拟的过盈量的变化曲线沿纵轴正向增大0.15 mm得到过盈量偏置曲线,该曲线在过盈量大于0.15 mm后的变化趋势和ANSYS仿真曲线变化趋势一致。

图11 数值模拟及仿真接触压应力变化对比Fig. 11 Comparisons of numerical simulation and simulation contact pressure stress change

图12 数值模拟过盈量变化及仿真径向位移差对比Fig. 12 Numerical simulations of interference change and comparison of simulated radial displacement difference
由图12 可见:有限元软件采用给定接触主从面径向位移差的方式施加初始过盈量。在过盈配合状态转变为间隙配合状态之前,轮轴接触面一直处于零间隙状态,故认为接触面间的径向位移差不变。当轮轴接触状态转变为间隙配合状态时,轮轴过盈配合的间隙在0.15 mm 的基础上继续增加。即当轮轴配合处于间隙配合状态时,有限元仿真得到的径向位移差为初始过盈量和间隙值之和。综上所述,对于含过盈量的轮轴过盈配合结构,在离心力载荷作用下仿真结果与理论数值模拟结果一致,验证了含初始过盈量的轴类过盈配合部件在离心载荷作用下的过盈量减小量公式推导的准确性。
4 结论
1) 不同旋转角速度下的过盈量及接触压应力的理论数值模拟结果与有限元仿真分析结果一致,验证了含初始过盈量的轴类过盈配合部件的过盈量减少量公式的准确性。
2) 随旋转角速度从0 rad/s 增大到1 207.73 rad/s,轮轴间接触压应力及过盈量不断减小,呈现非线性特征。当旋转角速度增大到960 rad/s 左右时,接触压应力及过盈量减小为零,此时,轮轴配合状态由过盈配合状态转变为间隙配合状态,轮轴间接触压应力及过盈量的理论数值模拟结果与有限元仿真结果一致。
3) 由于有限元软件采用对接触主从面施加径向位移差的方式施加初始过盈量,在过盈配合状态转变为间隙配合状态之前,轮轴接触面一直处于零间隙状态。在过盈量减小为零之前,轮轴过盈配合部件的接触面间的径向位移差一直不变。

