高频GARCH模型的最优抽样分析
程凌筠,宋泽芳,b*,张兴发,b,李莉丽
(广州大学 a.经济与统计学院; b.岭南统计科学研究院,广东 广州 510006)
作为资产收益变异程度的一种定量测度,波动率在金融时间序列的不同领域中都扮演着相当重要的角色,如衍生产品定价、对冲投资决策或风险价值(VaR)评估等,都与波动率密切相关。Engle[1]和Bollerslev[2]提出的自回归条件异方差模型,即 (G)ARCH模型,是目前最成熟、最常用的波动率建模模型之一。它已被广泛用于刻画和预测股票价格、商品期货、通货膨胀率和外汇等金融产品的波动率。随着计算机技术的飞速发展,采集、存储数据的成本不断降低,日内高频金融数据的获取也越来越方便。如何使用这类数据推进金融市场波动率的研究成为备受关注的焦点。其中一个方向是对日内波动率的刻画,常见的是基于日内高频交易数据所估计的日内真实波动率,通常称为已实现波动率。学者们运用不同的非线性度量方法提出了许多已实现波动率指标,如已实现方差、已实现双幂次变差和已实现极差等[3-5]。另一个方向是利用日内高频数据来改进日频波动率模型的估计精度。Visser[6]将日内高频信息引入到GARCH模型中,提出尺度模型和波动率代表模型,改进了GARCH模型参数估计的渐近方差,提高了估计的准确性。越来越多的研究也表明,由于高频数据蕴含了更丰富的资产价格变动信息,将高频信息引入低频波动率模型可以有效地提高模型参数的估计精度[7-13]。
在进行高频数据分析处理时,首要面对的是数据抽样问题,不同的频率会对估计的准确性造成不同的影响,即抽样频率过高容易有太多噪音,抽样频率过低又没有充分利用信息,因而关于抽样频率的择优选取就显得尤为重要。徐正国等[14]定义了微观结构误差(MSE)作为最优抽样频率的选择准则,其实证研究表明已实现波动率估计在10 min间隔的抽样频率下MSE达到最小。郭名媛等[15]则考虑MSE和测量误差之和为择优标准,以总误差最小的60 min为最优抽样间隔来计算赋权已实现波动率。唐勇等[16]分别依据已实现波动和已实现极差波动与积分波动之间误差项的渐近分布,给出了最优抽样频率的选择方法。李胜歌等[17]基于已实现双幂次变差和赋权已实现波动,给出了最优抽样频率选择方法。闵素芹等[18]比较了3种已实现波动率的最优抽样频率选择方法。杨建辉等[19]研究了不同抽样间隔下创业板指数已实现波动的分布特征及其最优采样间隔。
已有的这些研究中,学者们讨论高频数据的最优采样间隔大多是针对日内波动率刻画进行考虑,鲜有考虑日频波动率模型。本文进一步研究高频数据应用到日频波动率模型(GARCH)时的数据抽样问题。与传统的研究不同,本文的最优频率抽样问题可以比较方便地通过选择最优波动率代表来进行刻画。波动率代表是运用高频数据估计日频GARCH类模型时构造的一个重要统计量,它是由日内高频数据信息通过加工构造出的一个函数,不同的波动率代表对参数估计效果有直接影响。本文结合GARCH模型的3种估计方法,即基于对数正态分布的拟极大似然估计(log-Gaussian QMLE)、基于正态分布的拟极大似然估计(Gaussian QMLE)和基于拉普拉斯分布的拟极大指数似然估计(QMELE),讨论不同估计方法下最优波动率代表的选择问题及其在高频数据抽样频率的选择问题。
1 波动率代表模型
在日频数据下,使用GARCH(1,1) 模型对波动率进行建模,其形式为
yt=σtεt,
(1)
(2)
其中,yt为资产第t天的收益率;εt是服从均值为0,方差为1分布的一组独立同分布随机误差项,分布未知;对于∀t≥s,εt与ys相互独立;参数ω>0,α≥0,β≥0保证条件方差的非负性。
假设每天可观测到的金融资产价格过程为Pt(u),t=1,…,T,将日内的交易时间设为[0,1]区间,0≤u≤1。当u=1时,Pt(1)恰为第t天收盘价。定义第t天u时刻的高频对数收益率为
Yt(u)=100×[logPt(u)-logPt-1(1)],
即日内的收益过程。在模型(1)~模型(2)的基础上,Visser[6]考虑利用日内收益过程对日频GARCH模型进行扩展,得到如下尺度模型:
Yt(u)=σtZt(u),u∈[0,1],
(3)
(4)
其中,Zt(·)为标准过程,与σt相互独立;∀t≠s,Zt(·)与Zs(·)独立同分布;σt称为尺度参数。当u=1时,Yt(1)=yt,Zt(1)=εt,模型(3)~模型(4)即退化为日频GARCH模型。
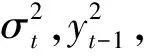
H(ρYt(u))=ρH(Yt(u))>0,∀ρ>0,
(第3.2节有举例详细介绍H函数)对每个交易日,根据正齐次性,由式(3)可得
Ht=H(Yt(u))=H(σtZt(u))=σtH(Zt(u)),
记zH,t=H(Zt(u))>0,由于Zt(u)是独立同分布的标准过程,因此,zH,t是独立同分布的随机变量序列。于是,波动率代表模型可表达为
Ht=σtzH,t,
(5)
(6)
上述模型中,所有变量都是同样的频率,日内高频数据信息体现在波动率代表量Ht上。当波动率代表量Ht=H(Yt(u))=H(Yt(1))=|Yt(1)|=|yt|时,可以看出模型(5)~模型(6)和模型(1)~模型(2)是等价的。一般情形下,模型(5)~模型(6)引入了高频数据信息,同时又和模型(1)~模型(2)具有相同的模型参数。因此,基于波动率代表模型(5)~模型(6)估计的参数,用到了更多的信息,有望得到更为精确的估计。
2 估计方法
对于波动率代表模型,现有的研究主要采用3种估计方法对模型中的未知参数进行估计,分别为对数正态分布拟极大似然估计、正态分布拟极大似然估计和拟极大指数似然估计,下面依次介绍3种方法对模型估计的过程,及估计量的渐近结果。
2.1 对数正态分布拟极大似然估计
Visser[6]给出了基于对数正态分布的拟极大似然估计(log-Gaussian QMLE)及其估计量的渐近正态结果,该方法是将拟极大似然估计(Gaussian QMLE)应用于对数波动率代表log(Ht)。
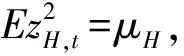
(7)
定义
于是有
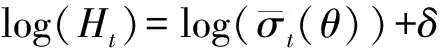
(8)
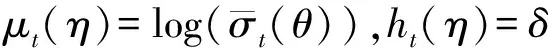
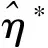
(9)
其中,
这里,G(θ)是关于θ和H,t的矩阵,与无关,具体证明见文献[6]。
2.2 正态分布拟极大似然估计
GARCH模型的常用估计方法是基于正态分布的拟极大似然估计(Gaussian QMLE)。为使用QMLE来估计θ=(ω,α,β)′,需要对残差项zH,t进行标准化,并对模型(5)~模型(6)稍作调整。
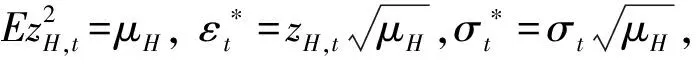
(10)
(11)
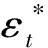
依据模型(10)~模型(11),θ*的QMLE定义为
(12)
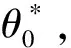
其中,
(13)
(14)
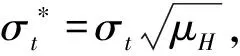
2.3 拟极大指数似然估计
在实际数据分析中,模型残差的分布是未知的,为了弱化矩条件,残差项常被假定为服从标准双指数分布(Laplace分布),因而基于该分布的拟极大指数似然估计(QMELE)也是常用的估计方法。
(15)
(16)
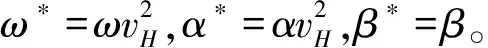
依据模型(15)~模型(16),θ*=(ω*,α*,β*)′的QMELE定义为
根据QMELE的渐近理论(Andersen等[21]),容易得到*的渐近分布为
其中,
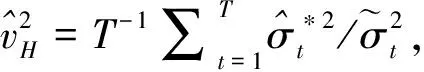
3 波动率代表的选择方法
3.1 波动率代表选择
从第2节可知,参数估计是通过极小化关于波动率代表的似然函数得到的,所以使用不同的波动率代表得到估计量的有效性是不同的,同时基于不同的估计方法,又会存在差异。因而选择合适的波动率代表是获取准确估计的重要前提。
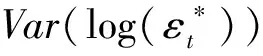
λ=Var(log(Ht)|Fn-1),
(17)
如果λ越小,参数估计的渐近方差就越小,即对应的波动率代表越好。因而,对于log-Gaussian QMLE,寻找最优的波动率代表即为寻找最小的λ值。
(2)对于正态分布拟极大似然估计,Visser[6]并未给出适用于其估计量的波动率代表选择方法。为此,在估计量渐近分布的基础上进行分析,以给出针对QMLE的波动率代表选择标准。
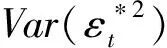
相应地,将上述两式进行相除,即得
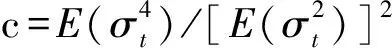
定义
(18)
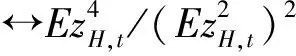
(3)对于拟极大指数似然估计,从渐近分布的角度出发同样可以得到选择最优波动率代表的标准。
于是,依据同样的推导思想,可以推得QMELE下波动率代表的选择标准为
(19)
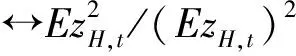
3.2 常见波动率代表
从高频对数收益率的表达式可以看出,计算波动率代表需要通过离散性抽样数据来得到,也就是需要固定一个时间间隔来采集日内的高频数据。令k表示日内时间间隔(单位:min),m表示在抽样频率k下一天内总的收益个数,Yt(uik) 表示第i次抽样的收益率,i=1,…,m。本文考虑以下4种波动率代表,作为模型中主要的选择比较:
①已实现波动率(RV):
②日内收益绝对值之和(RAV):
③已实现极差波动率(RVHL):
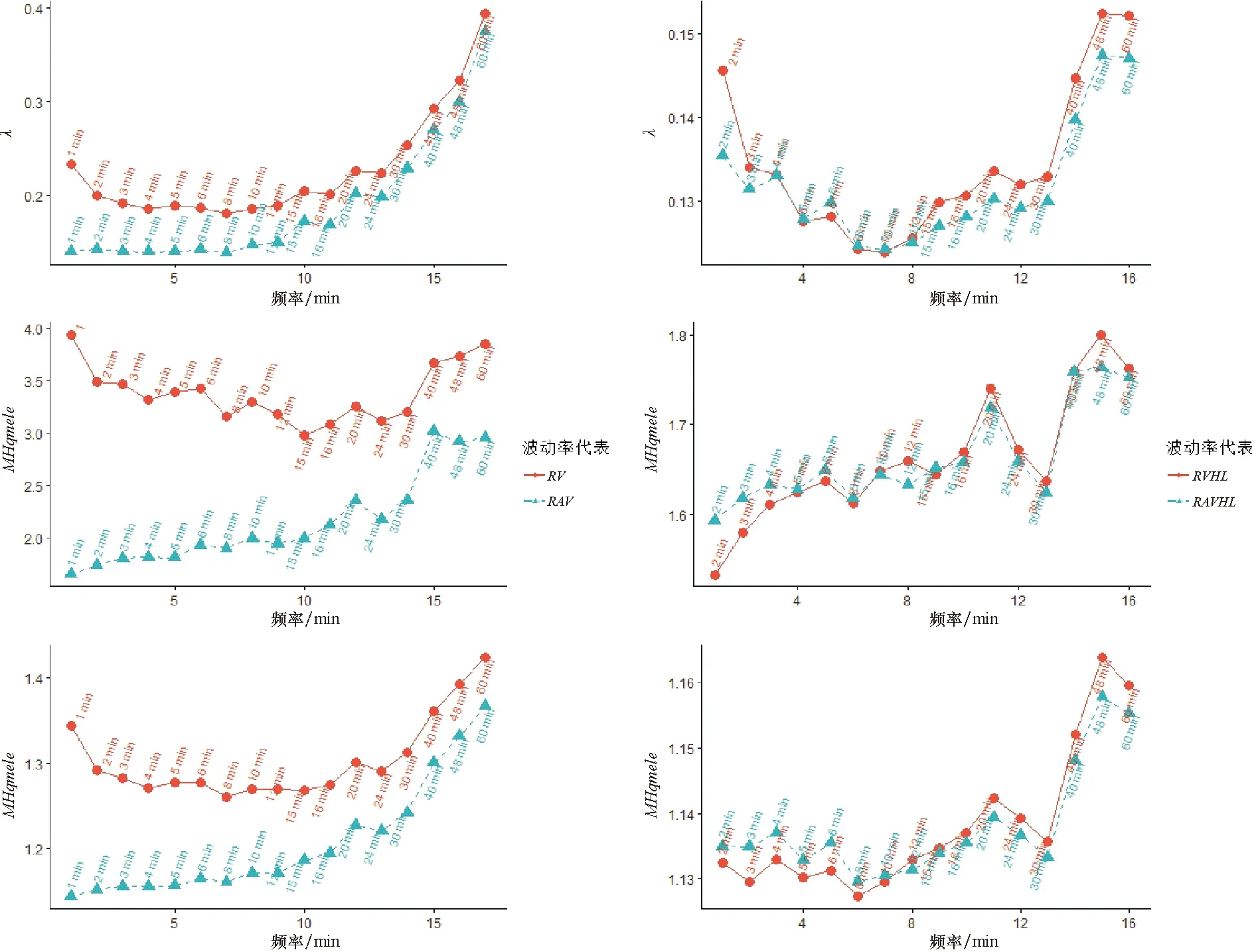
k(i-1)<Δi ④日内极差之和(RAVHL): minΔi(Yt(u))},k(i-1)<Δi 其中,Yt(u0)的值用Yt(0)=0 代替;maxΔi(Yt(u))和minΔi(Yt(u))分别为第i个时间段Δi中的收益率最大值和最小值。 以上RV、RAV、RVHL和RAVHL都是波动率代表Ht的具体例子,容易看出Ht的具体值会依赖于离散化的数据量个数,而将一天内的交易时间等分为多少段最合适即为最优抽样频率的问题。对于同一波动率代表,最优频率对应的Ht才是最优的。因而第3.1节给出的波动率代表选择标准可以提供一个选取最优抽样频率的方法,即波动率代表选择标准达到最小的时间频率为该波动率代表的最佳频率。 图1 波动率代表与抽样频率的关系图 表1 不同波动率代表在不同估计方法下的最优抽样频率 由表1和图1可看出,在不同波动率代表、不同频率、不同估计方法下,得到的估计量有效性均明显不同。通过比较分析发现: (1)在同一频率3种估计方法准则下,比较RV、RAV、RVHL和RAVHL后发现,RV的有效性最差,RAVHL和RVHL是较优的波动率代表函数。可以看到,在频率较高时(2~8 min)RAV和RVHL是最优的波动率代表函数,在频率较低时(10 min以上)RVHL的有效性表现更优。从指标的总体性看,两者相差不大,因此,RVHL和RAV都可作为最优的波动率函数。 (2)对同一波动率代表分别比较不同频率的表现可以发现,RV在不同频率下的有效性波动(数值大小变动)最大,随着抽样频率的增加,每种方法对应的数值大多是先递减后递增;相比之下,RVHL和RAVHL在不同频率下的有效性表现较为稳定,数值变动较小。 (3)比较最优抽样频率下的不同波动率代表发现,采用log-Gaussian QMLE时的最优波动率代表为10 min的RVHL(λ值最小),采用Gaussian QMLE时,则是2 min的RVHL最优(MHqmle值最小),而采用QMELE时是8 min的RVHL最优(MHqmele值最小),意味着在最优抽样频率下,无论使用什么估计方法,最优的波动率代表为RAV。 (4)每个波动率代表在相应频率上达到了最低点。不同波动率代表的曲线趋势存在显著差异。其中,RV的3条曲线均呈“低谷”状态;而RAV的3条曲线整体上均呈现递增趋势;RVHL和RAVHL随时间频率的变化趋势相同,或呈曲折递增,或大致地递减后再递增。 基于表1的结果,选择以2 min为间隔的RVHL进一步使用高斯QMLE估计出GARCH(1,1)模型的参数。该波动率代表具有最小的MHqmle值,那么根据式(12)和式(14)得到的估计量是最有效的QMLE,拟合沪深300指数收益率的GARCH(1,1)模型为 yt=σtεt, (20) (21) 于是,基于模型(20)~模型(21)可以获得更为准确的波动率估计。另外,若选用QMELE方法或对数正态分布QMLE方法,则分别需要以8 min和10 min的频率来构造RVHL,这样得到的QMELE和log-Gaussian QMLE的估计有效性是其中最好的,便于更准确地建立模型和估计波动率。 为了检验结果的稳健性,本文再将全样本分成了两个子样本(2017年9月1日-2018年6月30日和2018年7月1日-2019年7月12日),进行同样的波动率代表和频率选择分析。汇总结果见表2。 表2 子样本在最优波动率代表下的最优抽样频率 由表2可以发现: (1)同频率两个子样本下,RV波动率代表函数的有效性是最差的,RVHL和RAVHL仍然是两个差别不大的最优波动率代表函数。 (2)针对两个不同的样本,基于最优准则下选择的最优波动率代表会有所不同,同时在不同估计方法下选择的最优频率也会有所差异,表2中列出了两个子样本选择的最优波动率函数,以及不同估计方法下,基于最优波动率函数选择的最优频率。在2017年9月至2018年6月的第一个子样本中,选择的是RAVHL为最优波动率函数,3个估计方法下所对应的最优频率分别为8 min、30 min和10 min;在2018年7月至2019年7月的第二个子样本中,选择的是RVHL为最优波动率函数,3个估计方法下所对应的最优频率分别为3 min、2 min和2 min。 总的来说,本文可以得到一个稳健的结论是在全样本和子样本下,RVHL和RAVHL都可考虑选择为最优波动率函数,且不同频率下它们的表现模式也很相似。在选择最优频率时,除了考虑选择最优波动率函数,还要考虑不同的估计方法,同时也会依赖不同样本下的情况,但就整体而言,最优频率在2 min、8 min和10 min中选择,也启示了研究者和实践应用学者们在实际中对抽样频率进行谨慎选择。 通过波动率代表,可以将日内高频数据应用于改进GARCH模型的参数估计,不同的波动率代表提高估计精度的效果不同。本文介绍了波动率代表模型的3种估计方法,针对不同的估计方法给出了波动率代表的选择标准,并将这些准则进一步应用于解决高频数据抽样频率的选择问题。最后,采用沪深300指数的高频数据做实证研究,通过比较研究发现,不同波动率代表、不同抽样频率都会对GARCH参数估计量的有效性造成明显差异,而且在不同估计方法下的表现也不同。已实现极差波动率(RVHL)和日内极差波动率(RAVHL)是有效性表现较优的波动率代表,但它们都会依赖于抽样频率,其最优频率也会依赖具体的估计方法,但主要是在2~8 min中选择,具体的选择也需考虑更多的因素,未来可以考虑一个自适应样本的方法对最优频率进行选择。4 实 证
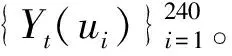


5 结 论

