建构弹性碰撞模型 “悟”入深度教学

霍良平

(旬阳第二中学,陕西 旬阳 725741)

深度教学是教师、学生、教材在课堂中的深度作用、融合过程.课堂教学中,教师是智者,在深度掌握学情(谁要学)、深度整合教学内容(学什么)、深度教学目标(预期效果)以及深度研究高考(解答问题)的基础上,主导学生以目标为导向、任务为驱动、知识为基础、会用为要求、提升为发展,实现学生以需要解决什么问题为目标导向,深度学习物理知识,深度悟透物理原理,深度归纳应用拓展.通过教师的深度输入,赢得学生的深度输出.本文以弹性碰撞模型的建构与应用为例,感悟践行深度教学.

1 强化教师主导作用,诱发课堂教学深度输入

以能解决生活中的碰撞类问题为目标导向,深度挖掘弹性碰撞模型教学,突出模型的基础性、规范性、学科性、生成性和应用性,预判、诱发、纠正学生在弹性碰撞模型构建中的错误点和疑难点,深度输入开启深度教学[1].

演示实验一:以牛顿摆为素材,引导学生改变不同的实验方案、观察不同的实验现象,诱发学生求知欲.

师:比如体育运动项目:台球、飞碟射击.生活中的交通事故:两辆汽车发生对碰、两辆汽车发生追尾,它们都是生活中的碰撞,今天我们来学习碰撞的基础知识,并用之解决生活中的碰撞问题.

建构弹性碰撞基础模型一个运动的小球与一个静止的小球在光滑的水平面上发生对心弹性碰撞.

对碰撞模型的认识误区碰撞瞬间完成,碰撞是一个状态,不是一个过程.

视频一:一个运动的台球与一个静止的台球发生对心碰撞.

师:同学们观察台球碰撞完成的快慢程度以及碰撞位置的变化情况?

生:两个台球的碰撞瞬间就完成了,台球的碰撞几乎在原位置就完成了.

师:同学们听到什么?

生:听到台球碰撞的撞击声,而且声音很强烈

师:同学们谈谈你对碰撞的总结?

生:两个台球的碰撞瞬间就完成,但是碰撞很剧烈.

对碰撞模型的认知难点发生弹性碰撞两个台球的形变很微弱,同学很难感知到形变.

师:两个台球的碰撞很剧烈,说明碰撞力很大,小球一定会发生形变,但是形变太小、太快,我们来不及观察到,你能设计一个方案,实现对形变过程的观察和分析吗?

设置物理情境:物体B的左侧固定一轻质弹簧,静止在光滑水平面上,物体A以速度v0与物体B发生正碰,如图1所示.

图1 物体A与物体B正碰

引导学生完成理论推理、分析并归纳出弹性碰撞模型的特征,如表1.

表1 弹性碰撞模型的特征

碰撞特点:碰撞完成需要经历两物体的压缩和分离过程,即碰撞是一个过程,但碰撞过程时间很短,碰撞剧烈,作用力很大[2].

对碰撞模型的认知易错点两物体发生弹性碰撞分离时,两物体的速度一定相反.

理论推导:质量为m1的小球A以速度v0与静止的质量为m2的小球B两球在光滑的水平面上发生弹性对心碰撞,求碰后A、B两球的速度分别为多少?

分析归类:

(1)当m1=m2时,v1=0 ,v2=v0碰后两物体互换速度;

(2)当m1m2时,v1为正值,v2v0碰后两个物体同向运动;

(3)当m1m2时,v1为负值,v2v0碰后两个物体反向运动.

说明:两个物体运动方向相反只是实现分离的一种情况.

2 落实学生主体地位,确保课堂教学深度输出

学生经历碰撞基础知识的学习过程,归纳出弹性碰撞的特点以及特征,从弹性碰撞类基础性问题的模仿处理入手,逐步拓展应用,尝试完成复杂的碰撞问题,甚至是创新、陌生情境下的碰撞问题,全面提升碰撞问题的理论水平,实现课堂深度输出[3].

2.1 模仿应用

学生能准确运用动量守恒以及动能守恒解决基础性的弹性碰撞问题.

例1如图2所示,在光滑的水平面上,质量为m1的小球A以速率v0向右运动,O点处有一质量为m2的小球B处于静止状态．小球A与小球B发生正碰后均向右运动,小球B被Q处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO.若小球间的碰撞及小球与墙壁间的碰撞都是弹性碰撞且碰撞时间极短,则两小球的质量之比m1∶m2为____.

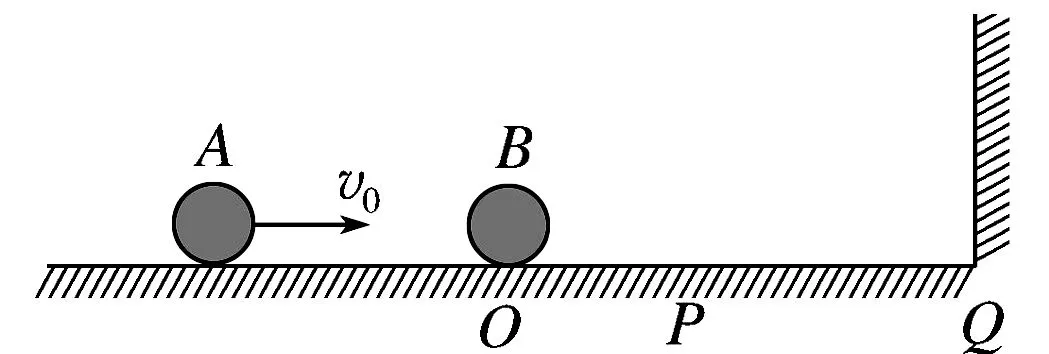
图2 小球A向小球B运动

学生模仿应用弹性碰撞的两个守恒定律,完成计算m1∶m2=3∶1

2.2 理解应用

通过对比分析弹性碰撞和非弹性碰撞,进一步加深对弹性碰撞的认识与理解.

以图1情境为例,同学们尝试分析,在物体A和B碰撞的压缩过程,若在弹簧压缩量达最大时,将弹簧锁定或弹簧发生了范性形变,即物体A和B无法实现分离过程,A、B两物体的碰撞还是弹性碰撞吗?

压缩过程中,A、B系统不受外力,满足动量守恒,减少的动能转化为弹簧的弹性势能或内能,动能不守恒.且弹性势能或内能无法再转化为系统的动能,即不属于弹性碰撞.物理学中将系统动能减少最大的碰撞叫完全非弹性碰撞.

结论:发生弹性碰撞的两个物体,必然要经历压缩过程和分离过程,且在分离的过程中,将压缩阶段累积的势能全部转化为系统的动能.

2.3 创新应用

模型舍去了原型的一些次要的细节、非本质的联系,以简化和理想化的形式再现原型的各种复杂结构、功能和联系,是连接理论和应用的桥梁.模型学习后的深度输出主要表现为学生能在陌生的碰撞情境中,分析、判断、运用弹性碰撞基础模型知识,正确处理复杂的实际问题[4],如例2.

例2如图3所示,一质量为M的滑块放置在光滑水平面上,滑块的一侧是一个四分之一圆弧EF,圆弧半径为R=1 m,E点切线水平,另有一质量为m的小球以初速度v0从E点冲上滑块,若小球刚好没有跃出圆弧的上端,已知M=4 m,重力加速度g=10 m/s2,不计一切摩擦,求小球的初速度v0以及小球再次回到水平面时的速度?

图3 小球向圆弧斜面运动

2.4 综合应用

碰撞类情境问题种类繁杂,但碰撞基础模型知识是一样的,学生学习的深度输出就表现为:能否正确运用碰撞的特点、特征处理不同物理碰撞情境问题,能否灵活运用碰撞模型基础知识准确解答综合类碰撞问题,如例3.

例3如图4所示,光滑的水平杆上套有一质量为1 kg、可沿杆自由滑动的滑块,滑块下方通过一根长为1 m的轻绳悬挂着质量为0.99 kg的木块.开始时滑块和木块均静止,现有质量为10 g的子弹以500 m/s的水平速度击中木块并留在其中,重力加速度g=10 m/s2,求木块能上升的最大高度以及再次回到最低位置时的速度?

图4 子弹射向木块

课堂为教学的输入与输出提供舞台,教师要合理利用舞台导演“深度课堂”这部戏,做好基础知识内涵式深度备课是前提,让学生清晰课堂任务目标是关键,引导、启发学生领悟知识、熟练运用知识处理学科情境化问题是重点,实现学生深度输出是目标.以教师深度的教为入,学生深度的学为出,实现深度课堂.