基于概率稀疏自注意力的IGBT模块剩余寿命跨工况预测

钟智伟, 王誉翔, 黄亦翔, 肖登宇, 夏鹏程, 刘成良

(上海交通大学 机械与动力工程学院, 上海 200240)

绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)是一种电压驱动式功率半导体器件,具有较小的导通电阻、饱和压降及驱动电流,同时兼具较快的开关速度[1],这些优势特性使得IGBT在工业界被广泛应用,包括以航空航天为首的重工业领域以及电动汽车一类的新兴领域[2].工业界调查显示, 功率器件是电力电子系统中最易失效的部件之一[3].研究证明,热疲劳是导致IGBT模块失效的最主要因素[4].随着IGBT模块应用领域的扩大,对其可靠性和使用寿命的要求也不断提高,剩余寿命预测可为元件维修更换提供参考,减少检修和停机时间,提升系统整体可靠性[5].

IGBT剩余寿命预测的方法根据预测机理主要分为基于物理模型、基于解析模型以及基于数据驱动共3类.基于物理模型的方法在实际使用中,通常根据IGBT模块实际参数建立物理模型并通过有限元分析来预测剩余寿命.Huang等[6]基于IGBT模块键合线的应力应变模型,建立电-热-力多物理场耦合模型,对键合线的寿命进行分析.基于物理模型的预测方法在实际工况下难以应用,需通过专家知识建立合适的物理模型,且需要获取产品的几何、电气参数.基于解析模型的预测方法根据IGBT模块运行过程的失效数据建立老化循环次数和指定物理量之间的数学模型.Coffin-Manson模型和Lesit模型建立了结温与IGBT模块寿命之间的关系[7],但上述两个模型仅考虑单一物理变量的影响;Norris-Landzberg模型和Bayerer模型等考虑多物理量对寿命的影响,一定程度上提高了预测的准确性[8].基于解析模型的预测方法需大量实验数据,且需手工建立合适的数学模型,难度大.基于数据驱动的方法通过挖掘IGBT模块运行的各种数据信息,结合预测模型对寿命进行预测,无需复杂的数学建模和专家知识.刘子英等[9]以集射极关断电压峰值为失效依据,建立Elman神经网络模型进行IGBT模块的寿命预测;葛建文等[10]基于IGBT模块的壳温、结温等数据计算模块热阻,利用Transformer神经网络来预测剩余寿命.上述方法都是在单个工况的IGBT模块上基于故障前历史数据进行预测,而更可靠的方法是使用一个在IGBT模块完整退化过程数据上训练得到的模型来预测其他IGBT模块的寿命,但实际情况下,不同电压电流工况下IGBT模块的各种参数差别较大,模型适应性差.

为解决现有序列预测方法无法并行处理、效率低及跨工况预测效果差的问题,提出一种基于概率稀疏注意力与迁移学习的方法,实现从已获取全生命周期退化数据的源工况迁移到全新目标工况IGBT模块寿命预测,基于IGBT模块的加速老化试验原理,搭建试验平台,获取不同工况下IGBT模块老化过程中的瞬态热阻数据,进行跨工况剩余寿命预测对比实验。实验结果表明,本方法在IGBT模块剩余寿命的跨工况预测效果上明显优于其他对比方法.

1 IGBT剩余寿命预测方法

1.1 概率稀疏自注意力

Transformer[11]的出现使得自注意力机制在各个研究领域占据了一定的统治地位,尤其是在序列预测方面.在剩余寿命预测领域,自注意力机制已经应用于轴承[12]和涡扇引擎[13]的研究中.

自注意力机制本质上是对样本进行权重分配,注意力函数被用来实现这种机制,其作用是将一个查询向量和一组键值向量映射到输出向量上.对于输入X∈RL×d中的一个样本向量xi∈Rd,首先计算出对应的查询向量、键向量、值向量:

(1)

(2)

(3)

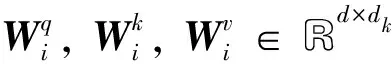
(4)

为了关注不同特征在不同表征子空间的信息,通常会采用多头注意力方式,表达式为

M(Q,K,V)=

(5)

hi=Attention(Q,K,V)i

(6)

式中:WM∈RHdk×d;dk=d/H,d为嵌入空间维度;H为多头的数量.

但上述传统自注意力的时间复杂度和空间复杂度较高.经研究发现,传统自注意力机制不同的查询值对应的注意力权值分布并非全都有所侧重,部分可能趋近于均匀分布,被称为惰性分布,相应有所侧重的部分被称为激活分布,如图1所示.

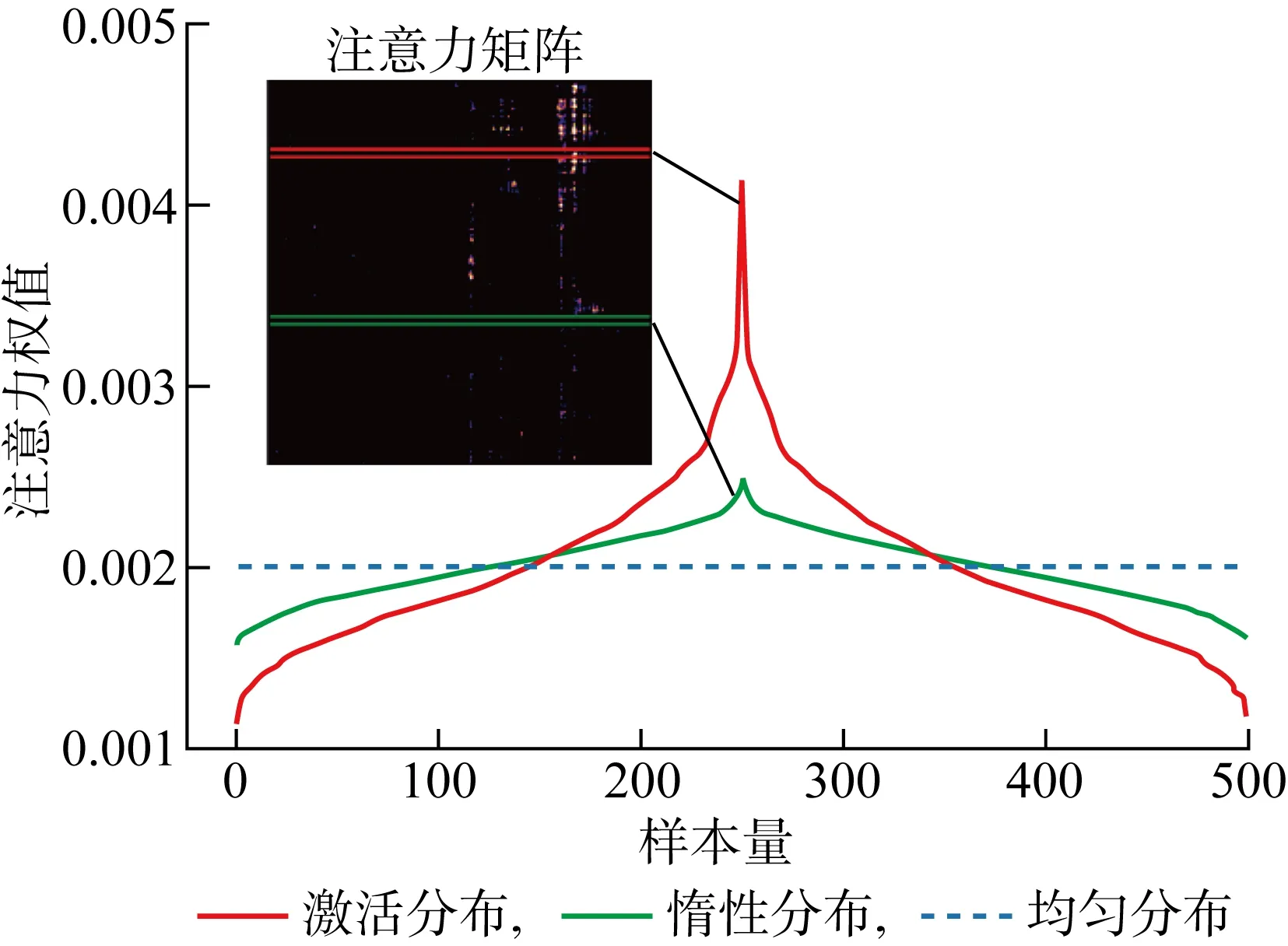
图1 经典自注意力权重分布Fig.1 Canonical self-attention weight distribution

利用KL散度可以对这两种分布度量进行区分,得到第i个查询向量与对应键向量的近似概率分布评估函数[14]为

(7)

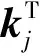
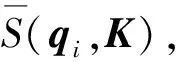
式(1)～(7)说明了概率稀疏自注意力机制优化计算效率的数学原理,为了实际对比其计算速度优化效果,将在后文与传统自注意力机制进行对比.

1.2 基于概率稀疏自注意力与迁移学习的预测模型

基于概率稀疏自注意力机制和迁移学习构建的剩余寿命预测模型如图2所示.图中,T为当前时刻,t为起始时刻,MK-MMD为多核最大均值差异.

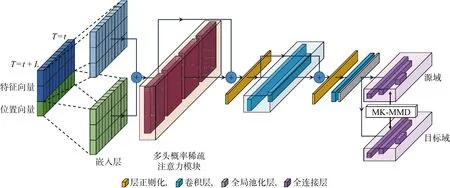
图2 所提出的模型结构Fig.2 Proposed model structure

IGBT模块退化过程数据包含时序信息,在不使用循环神经网络(RNN)结构的情况下,位置编码是使模型能够有效利用这种时序信息的方法[15].对于一个输入特征序列x=(x1, …,xL),xi∈Rf,f为提取特征维度,将其映射到高维空间得到V=(v1, …,vL),vi∈Rd,对于输入序列的位置向量p=(0, …,i, …,L),i为序列中每个样本的位置序号,使用正余弦位置编码方式[11]将其映射到相同维度的高维空间得到P=(p1, …,pL),pi∈Rd,最终嵌入层的输出为

X=V+P

(8)

式(8)为多头概率稀疏自注意模块的输入,使得注意力机制能充分利用数据特征信息及其潜在的时间先后关系.多头概率稀疏自注意模块将传统多头自注意力中单头的注意力计算方法改为前文所述的概率稀疏注意力计算方法,并加上残差连接,将序列中对预测结果影响更大的样本赋予更高的权重,使模型提取到更有效的信息.后面的卷积层、池化层则是为了进一步提取深度特征,保留有效信息,去掉冗余信息,避免全连接层参数量过大.最后的全连接层则是根据深度特征信息进行拟合,输出预测的剩余寿命.

IGBT模块在不同工况下的衰退过程特征变化规律差异较大,在一个特定工况下训练的模型很难直接预测其他工况下IGBT模块剩余寿命,故模型需要进行领域自适应,减少源域和目标域特征分布的差异性,使其提取到的深度特征更具有泛化性.本文在全连接网络层使用MK-MMD[16]来衡量源域和目标域的差异,多核函数定义为

(9)

式中:k为多核函数;ku为单个核函数;βu为每个核函数的权重,则MK-MMD计算公式为

(10)

最终该模型的优化目标由损失函数和MK-MMD距离组成:

(11)

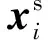
式(9)～(11)说明了领域自适应原理,通过修改损失函数对模型参数优化进行一定限制,从而减小不同域深度特征的差异,最终提升不同域下模型的预测性能.

2 IGBT加速老化试验

2.1 加速老化试验原理

IGBT模块在实际运行过程中的寿命周期较长[17],短时间内很难收集到足够的退化过程数据.加速老化试验在保证相同失效机理的前提下,提升试验产品所承受的应力水平,加速其失效,目的是快速获取产品退化数据,分析失效原理,根据高应力下产品的老化规律对正常情况下的产品进行寿命预测[18].

绝大部分IGBT模块失效由热应力引起,加速老化试验通过对IGBT模块施加热激励来提高热应力水平,从而加速其老化过程.根据应力施加方式的不同,加速老化试验采用的应力施加方式主要有恒定应力、步进应力和序进应力[19].恒定应力具有试验理论成熟、试验过程简单成功率高的特点,故本文将其作为施加方式.根据热激励的来源,热激励施加方式包括主动激励和被动激励[20],前者通过提高主功率电路内的电压电流使器件自身发热以达到设定温度;后者通过改变环境温度来使器件达到设定温度.主动激励的方式无需借助恒温箱类额外设备,试验方案简单、成本低且更符合实际运行工况,故选择主动热激励的方式.

2.2 加速老化试验台

根据加速老化试验原理,搭建加速老化试验台,其电路原理图如图3所示.图中,GND为接地端,ENA为使能信号端,FPGA为现场可编程门阵列,PC为计算机,R为电阻,L为电感.

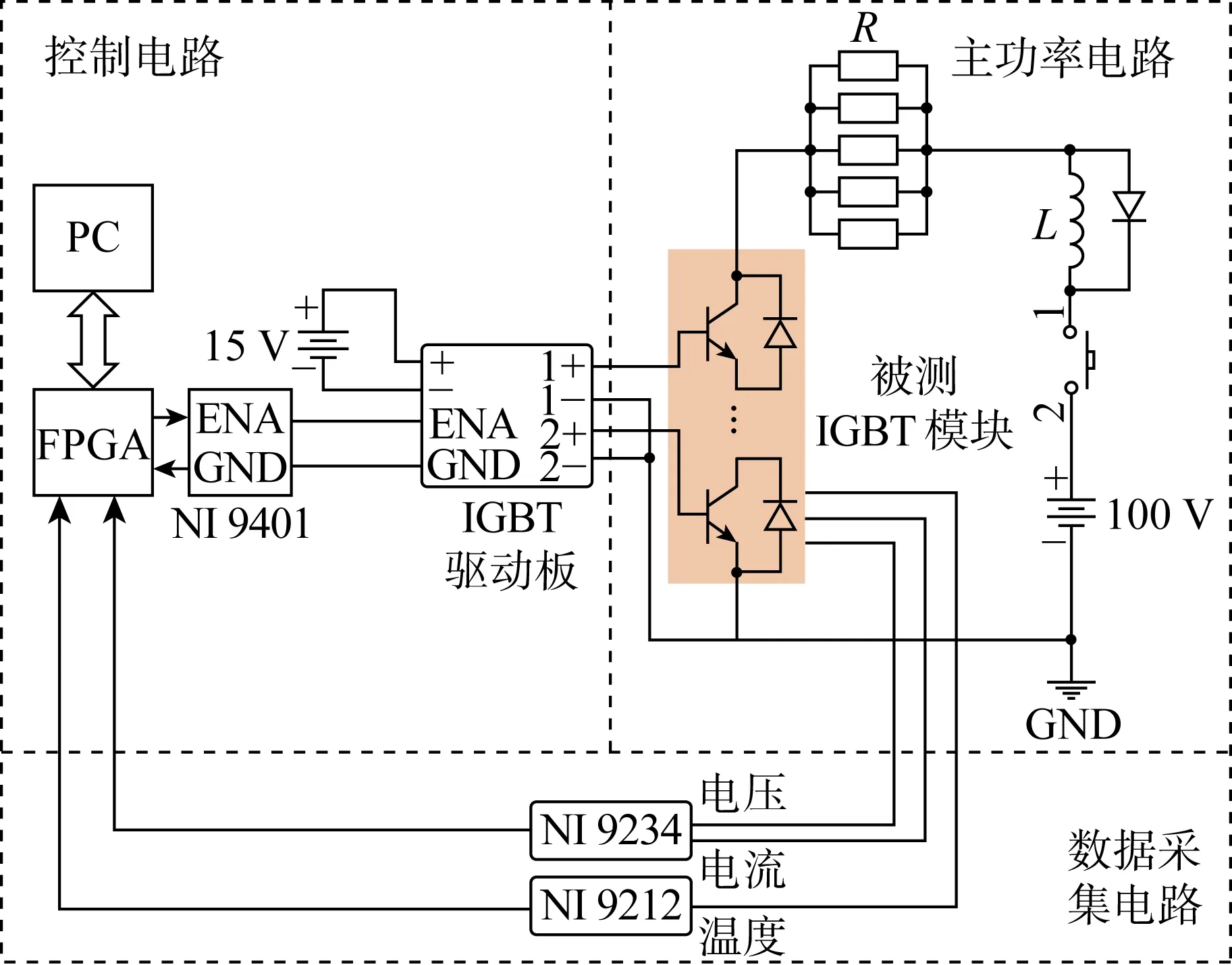
图3 加速老化试验台电路原理图Fig.3 Circuit schematic diagram of accelerated aging test bench

加速老化试验台实物如图4所示,核心试验台根据不同层的设备,分为电源层、负载层、IGBT模块层及驱动数采层.温度信号采集使用的传感器为超细焊点K型热电偶,测量范围为-20～200 ℃,通过NI 9212采集卡将热电偶的电压转化为实际温度,电压电流通过NI 9243采集卡进行采集.

图4 IGBT加速老化试验台Fig.4 IGBT accelerated aging test bench

2.3 加速老化试验方案与结果

Smet等[21]研究发现结温差ΔTj和平均结温Tjm是决定IGBT寿命的重要因素,二者的表达式分别为

ΔTj=Tj_max-Tj_min

(12)

(13)

式中:Tj_min为结温的最小值;Tj_max为结温的最大值.

本文主要研究相同结温差下不同平均结温工况IGBT模块焊料层疲劳导致的寿命问题,瞬态热阻是表征焊料层失效程度的关键参数[22],因此以其作为寿命表征参数.研究表明,当结温差大于100 ℃时,IGBT模块以键合线失效为主;当结温差小于 80 ℃ 时,以焊料层失效为主[23].将控制IGBT模块在结温波动范围为80 ℃但平均结温不同的情况下进行加速老化试验,初始状态的电流循环曲线和温度循环曲线如图5所示.图中,Tj为结温,Tp为壳温,I为通过IGBT模块的集射极电流.

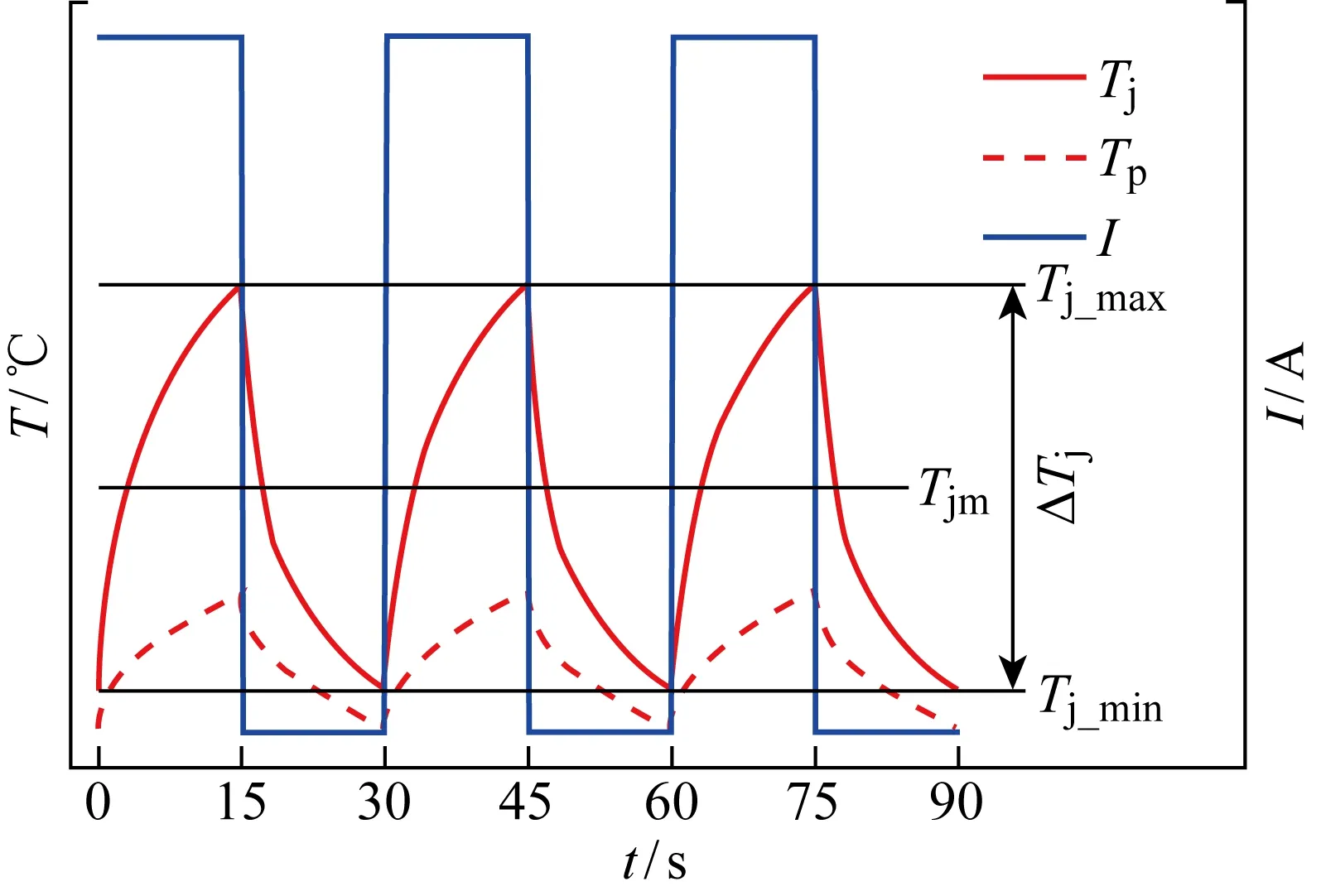
图5 直流老化循环曲线Fig.5 Curves of DC aging cycle

每个循环周期开始时,IGBT模块被导通,结温Tj不断上升直至到达设定的最大值Tj_max,此时IGBT模块被关断并开启冷却系统,直到结温Tj下降到设定的最小值Tj_min,如此不断重复.统一工况实验下随着循环次数不断增加,Tj_min和Tj_max不变,而不同工况实验下Tj_min和Tj_max不同.

实验选择的IGBT模块型号为英飞凌FF50R12RT4,最高工作温度为150 ℃,额定电流为50 A.在3种工况下进行加速老化试验,均出现热阻增加的焊料层失效形式,实验工况及对应结果如表1所示.不同工况下Tj_min和Tj_max对应图5中的Tj_min和Tj_max,N为IGBT模块失效时老化循环次数.

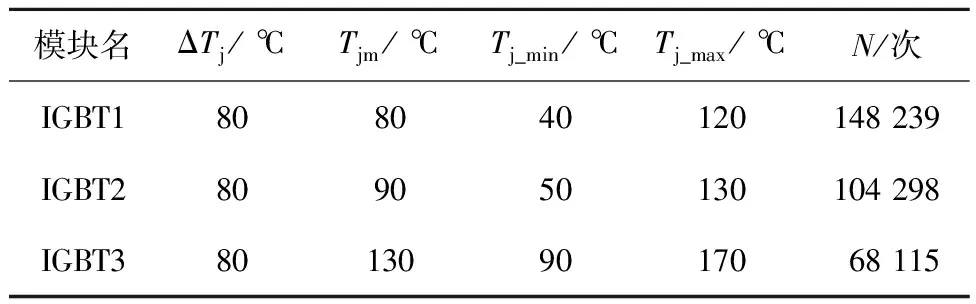
表1 老化试验工况及结果Tab.1 Aging test conditions and results

在相同结温差下,随着平均结温的增加,IGBT模块寿命减少,符合Smet等[21]的研究结果.

IGBT模块热阻在其导通一段时间内是变化的,为了充分利用热阻信息,可根据下式计算时刻t模块的瞬态热阻:

(14)

式中:Tj(t),Tp(t)分别为t时刻IGBT模块的结温和壳温;Vce_on(t),I(t)分别为t时刻IGBT模块集射极的电压和电流.实际采集过程只能获得离散数据,每隔0.1 s采集一次数据.

以IGBT3为例,经过不同次数老化循环周期后一个完整周期内瞬态热阻的变化曲线如图6所示.实验初期,瞬态热阻的变化与老化循环次数的关系并不明显,随着老化循环次数的继续增加,模块瞬态热阻的最大值明显不断增加,曲线斜率也相应变化,且瞬态热阻上升的时间即IGBT模块导通时间不断减少,这是因为随着老化循环次数的增加,模块热阻增加,结温上升速度会加快,从Tj_min上升到Tj_max需要的时间也会相应减少.图5则对应图6中循环次数较低热阻曲线的电压电流变化过程,随着老化循环次数的增加IGBT导通的时间会相应缩短.

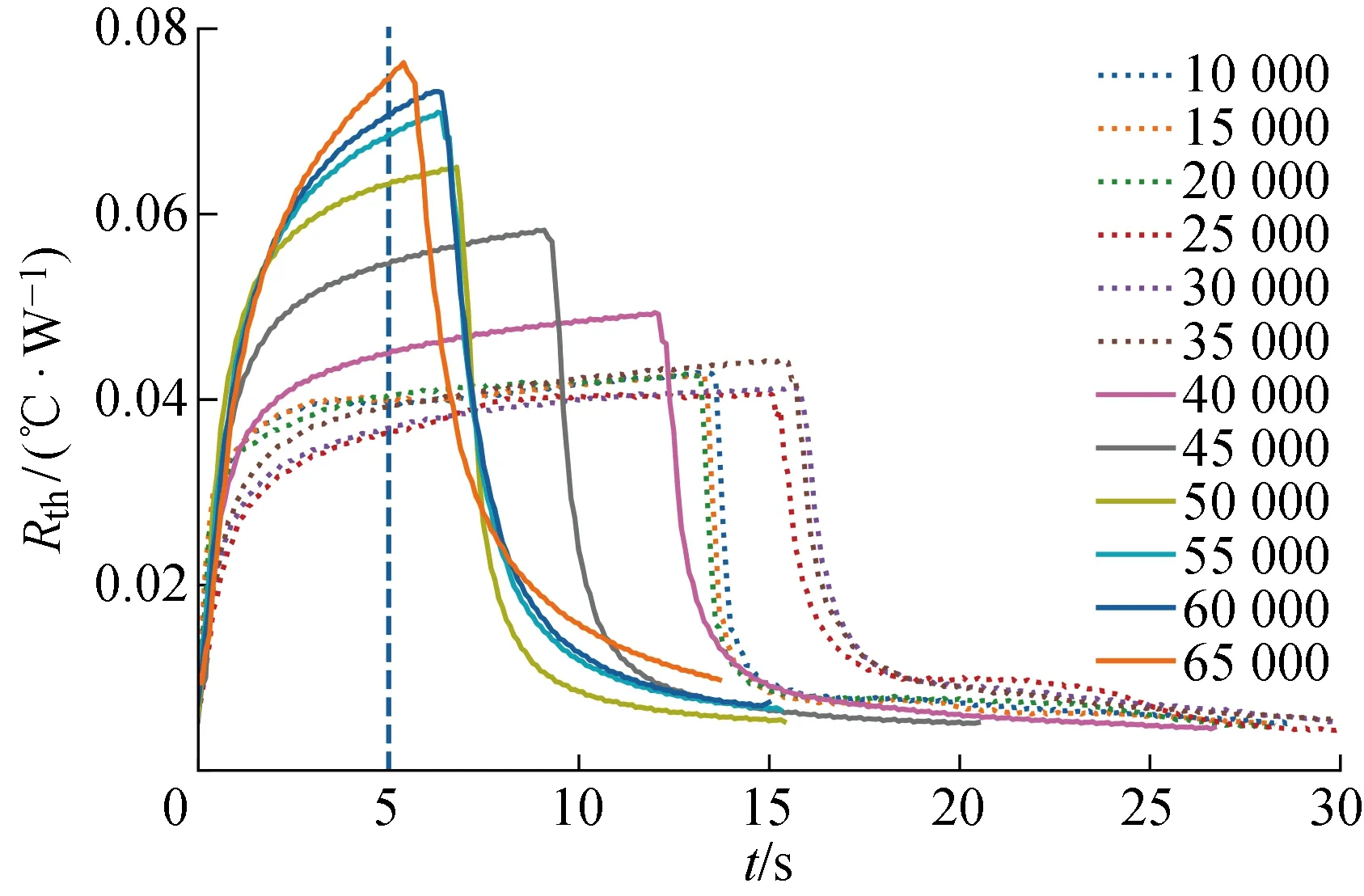
图6 不同老化循环次数IGBT3的瞬态热阻Fig.6 Transient thermal resistance of IGBT3 with different aging cycles

因本文提出的预测模型只能输入固定长度的序列数据,为统一不同老化循环次数数据序列长度,取前5 s瞬态热阻数据进行IGBT模块寿命预测,保证数据都位于热阻上升阶段(见图6),避免数据所处阶段不同对预测结果造成影响.

3 实验与对比分析

3.1 有效数据截取

IGBT模块与轴承等部件类似,在很长时间内会保持稳定的健康状态[24],这段时间内特征信息没有衰退信息,故无法从最初时刻开始预测剩余寿命,而应该从表现出衰退趋势的时刻开始预测.基于导通后5 s内瞬态热阻最大值使用3σ准则[25]确定模块开始退化的时刻,同样以IGBT3为例进行说明,如图7所示.基于前 10 000 个循环热阻最大值计算得到3σ范围,当连续25个点超过该范围,则认为对应的老化循环次数为IGBT模块开始退化的时刻.

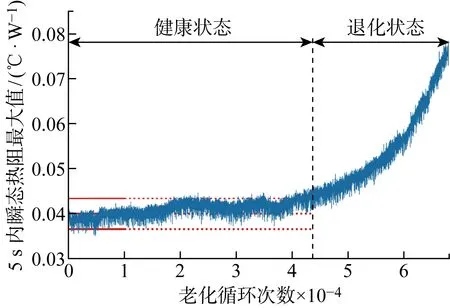
图7 IGBT3开始退化时刻的确定Fig.7 Determination of the time when IGBT3 starting to degrade

3.2 瞬态热阻特征提取与筛选

端到端模型对数据量要求大且会排除有用的人工设计,对每个循环的瞬态热阻数据进行特征提取与筛选后再输入网络模型,达到简化模型的效果.共提取了22个特征,如表2所示.

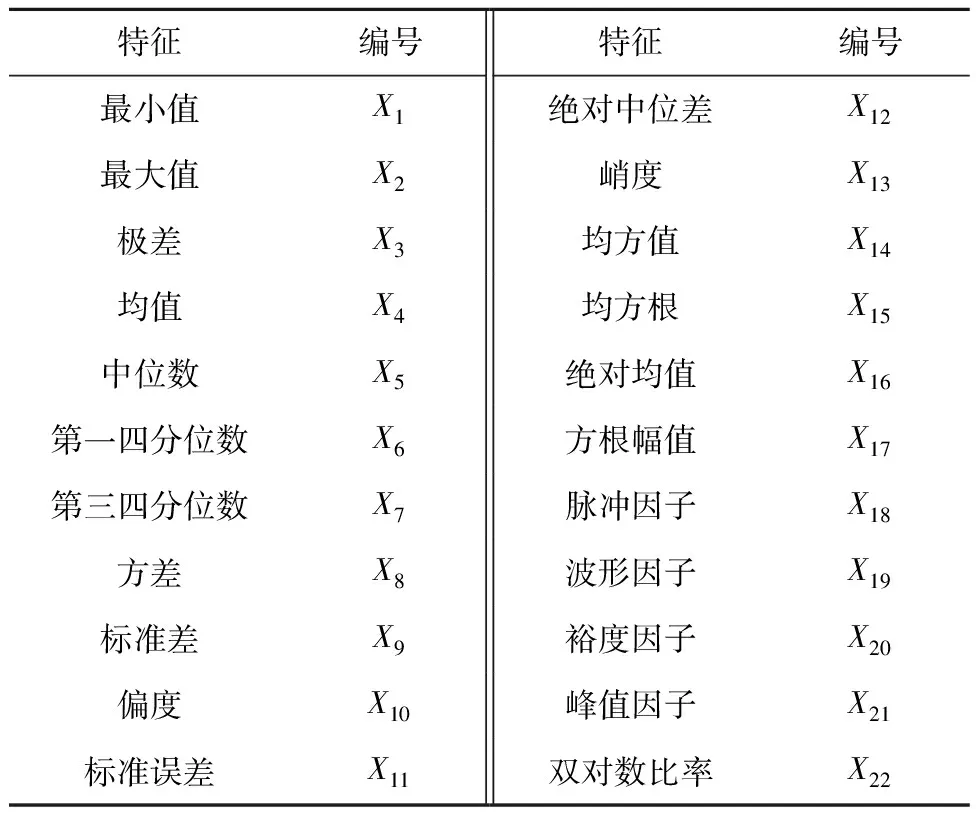
表2 瞬态热阻特征Tab.2 Features of transient thermal resistance

为了去掉与IGBT模块退化过程无关信息,对所提特征进行筛选.相关性可以衡量特征的变化趋势与衰退过程的一致性,若某特征的相关性计算结果越大,说明特征能更好地表征衰退过程的变化,表达式为

Corr=

(15)

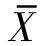
IGBT模块的剩余寿命应该是关于老化循环次数单调的,若某特征单调性计算结果越大,则说明其能更好地表征衰退过程,单调性的表达式为

(16)

式中:ΔX为特征在相邻循环的变化值;N(ΔX>0)为变化值大于0的数量;N(ΔX<0)为变化值小于0的数量.

为了兼顾上述两个指标,定义特征选择标准为二者的均值:

(17)

截取每个实验工况下IGBT模块处于退化状态的数据作为有效数据,分别以不同工况下有效数据进行特征表征能力计算并最终取其平均值,设定特征选择阈值为0.5,最终共筛选出12个有效特征作为后续模型的输入,如图8所示.其中,12个有效特征对应图中12个绿色柱状图.

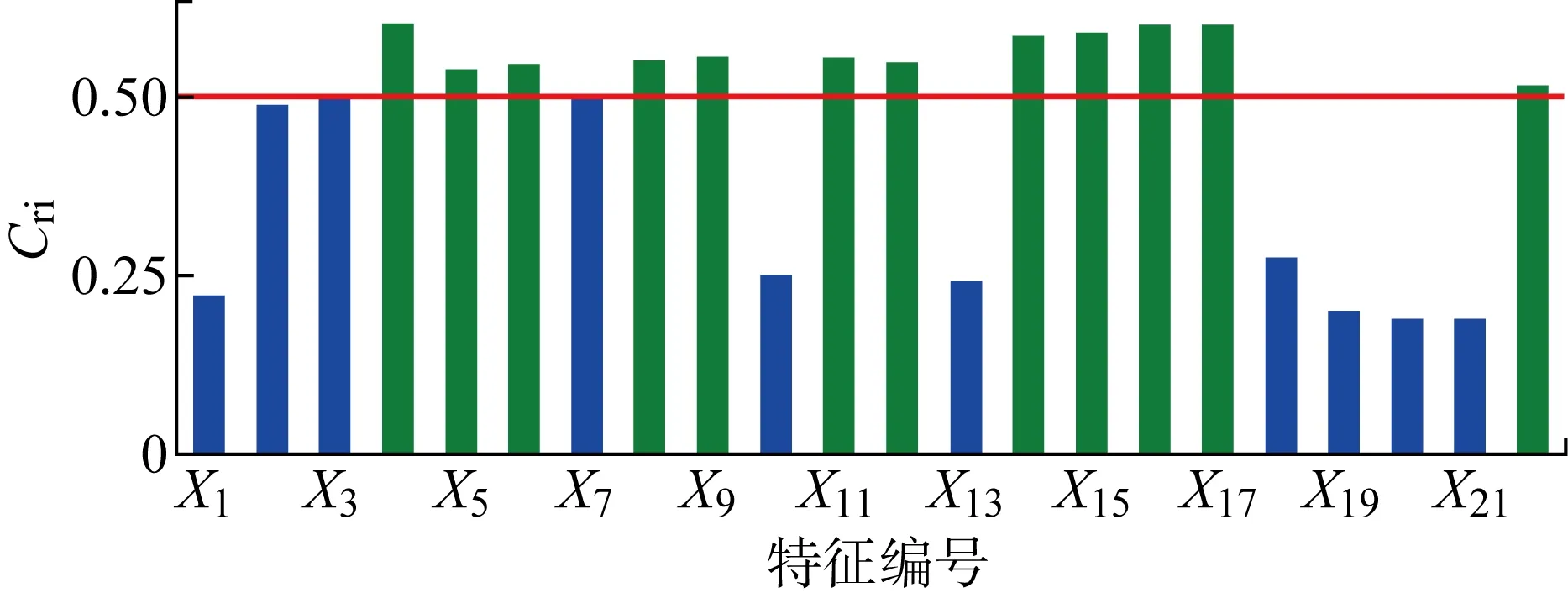
图8 衰退特征表征能力Fig.8 Degradation characteristic ability

3.3 模型设置

对于所有实验模型,输入为筛选得到的特征序列,输出为IGBT模块对应老化循环次数下的剩余寿命比例.输入序列长度设为50,即每个输入样本为x=(xt, …,xt+50),xy∈R12.具体输入样本来源于不同工况下IGBT热阻特征向量的滑动窗口切分,如第1个样本为x1=(x0, …,x50),第2个样本为x2=(x1, …,x51),其中xy为y个老化循环热阻特征向量,因此IGBT1对应样本数为 148 190,IGBT2对应样本数为 104 249,IGBT3对应样本数为 68 066.训练集或测试集会根据工况选择对应IGBT切分得到的整个样本集.

参数优化方法选择随机梯度下降算法,学习率初始值设为0.01,每轮训练衰减为原来的1/2,每次迭代使用的数据样本数量(batchsize)设为64,模型主要参数如表3所示.

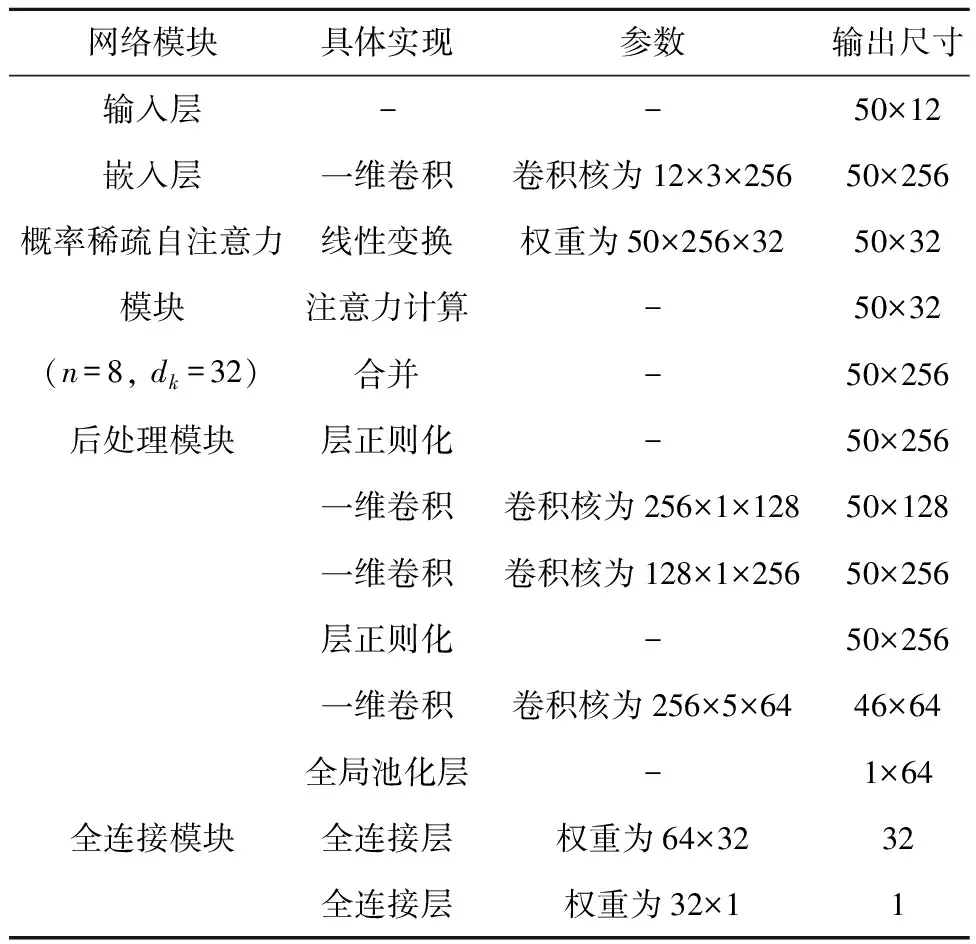
表3 模型结构参数Tab.3 Parameters of model structure

3.4 结果对比分析

使用提出的模型在3个实验工况下两两进行迁移,对比了由多层感知机组成的gMLP[26]和经典时序模型长短期记忆网络LSTM这两个无迁移模型及这两个模型结合传统迁移方法迁移成分分析(TCA)[27]和CORAL[28]的预测效果,如表4和图9所示.为了直观比较各模型的预测性能,选择均方误差MSE和平均绝对误差(MAE)评价指标进行对比衡量:

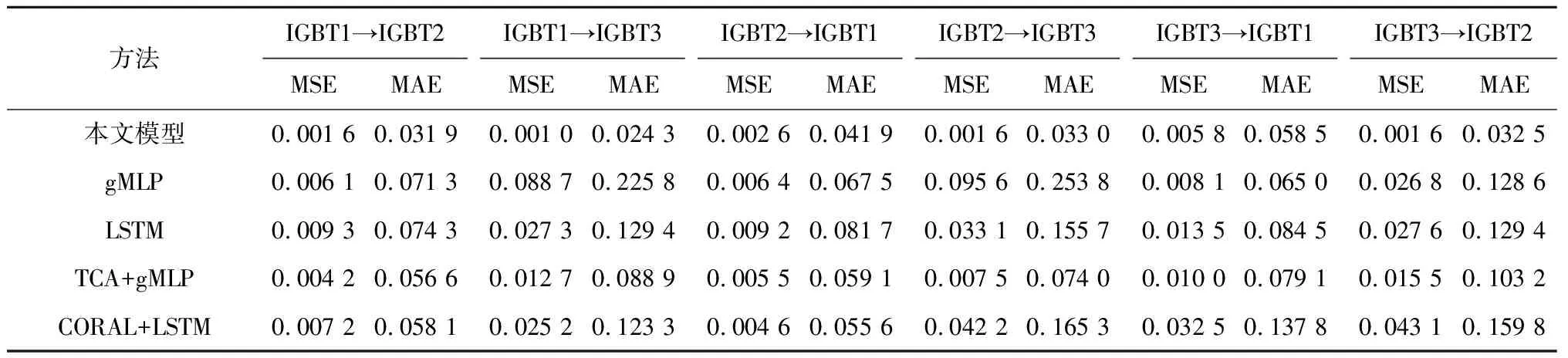
表4 不同模型预测结果Tab.4 Prediction results of different models

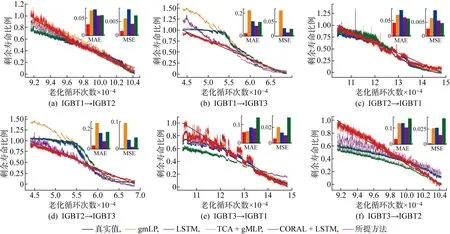
图9 不同模型IGBT模块剩余寿命预测结果Fig.9 IGBT module RUL prediction results of different models

(18)

(19)

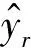
IGBT1→IGBT2为一个迁移任务案例简要叙述其意义,如图9(a)所示.IGBT1代表源域,即有标签数据集合;IGBT2代表目标域,该部分只有特征数据,没有剩余寿命标签;无迁移模型只使用有标签的源域数据进行监督训练,直接在目标域数据上进行预测,即训练集为有标签源域数据集,测试集为目标域数据集.本文提出模型在内的迁移模型则在源域数据监督学习,在目标域数据上无监督学习并预测剩余寿命,即训练集为有标签源域数据和无标签目标域数据,测试集为目标域数据.结果可知,本文提出的模型在所有迁移任务上实现了最好的预测效果,在IGBT模块退化的整个过程都能较好地预测其剩余寿命.

进一步分析发现进行实验的无迁移模型和迁移模型都能在IGBT模块衰退后期较好地预测剩余寿命,说明提取的IGBT模块的瞬态热阻特征在衰退后期的变化规律比较一致,差异性较小,而早期特征则有较大差异,因此迁移模型在大部分任务上的预测效果要明显优于无迁移模型.IGBT1和IGBT2的实验平均结温较接近,所有对比方法在这两个工况之间的任务预测效果都优于其他任务,符合实际情况,而这两个IGBT模块的实验工况与剩余一个工况差别都较大,对比方法效果均出现明显下降,CORAL+LSTM方法甚至在IGBT3→IGBT2和IGBT3→IGBT1任务中出现了明显的负迁移现象, 证明IGBT3模块的实验数据与其余两个模块数据域间差距大,且CORAL方法无法有效地将它们的数据映射到一个合适的空间来减小这种差距.

为验证本文模型使用MK-MMD进行领域自适应的必要性,在6个任务上进行领域自适应前(不使用MK-MMD,直接在源域上训练,目标域上预测)和领域自适应后的结果对比,如图10所示.领域自适应后,模型预测结果的MSE和MAE相比领域自适应前均有不同程度下降,在IGBT1和IGBT2的相互迁移上提升最小,与前文所述工况相近,无迁移模型预测效果相对较好;其他迁移任务上由于工况差别较大,不使用MK-MMD进行领域自适应模型很难学习到目标域下特征在衰退过程中的变化趋势;同时,从严苛工况到相对宽松工况的迁移效果更好,例如IGBT3→IGBT1优于IGBT1→IGBT3,IGBT3→IGBT2优于IGBT3→IGBT2,分析认为是严苛工况下短时间内退化信息更明显、信噪比更高、噪声影响更小,模型能够学习到更有效的特征.

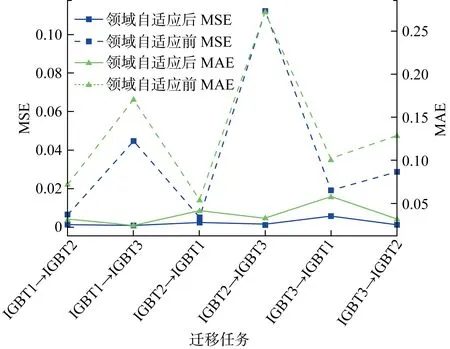
图10 领域自适应前后结果对比Fig.10 Comparison of results before and after domain adaptation

为了更直观显示MK-MMD对模型提取特征的影响,使用t分布随机近邻嵌入(t-SNE)将领域自适应前后源域和目标域数据在全连接第一层的特征向量降至2维,数据从剩余寿命比例由1到0对应的样本中均匀抽样.

领域自适应前,IGBT模块不断老化过程中,目标域和源域的深度特征整体分布有很大差异,只有在老化到一定程度时,特征变化才有相对接近的变化趋势,与前文实验结果显示的所有模型在老化后半段预测效果相对更好的现象符合,如图11(a)所示.领域自适应后,在整个衰退过程中,模型学习到的目标域深度特征和源域分布都较接近,因此使用MK-MMD进行领域自适应是必要的,如图11(b)所示.图11中颜色从深到浅表示输入样本的剩余生命比例标签从1到0.

图11 领域自适应前后全连接层源域和目标域的特征表示Fig.11 Feature representation of source domain and target domain of fully connected layer before and after domain adaptation

为验证概率稀疏自注意力机制相比传统自注意力机制在降低计算开销、加快计算速度的同时,也能很好保持预测性能,将模型的注意力模块替换为传统注意力模块,并分别在6个迁移任务下进行多次实验,得到了每种迁移任务下相对表4中4种对比方法表现最差的预测结果提升,如图12所示,以及单次迭代(batch)下使用两种注意力机制模型的平均计算时间对比(GPU为RTX3070),如表5所示.

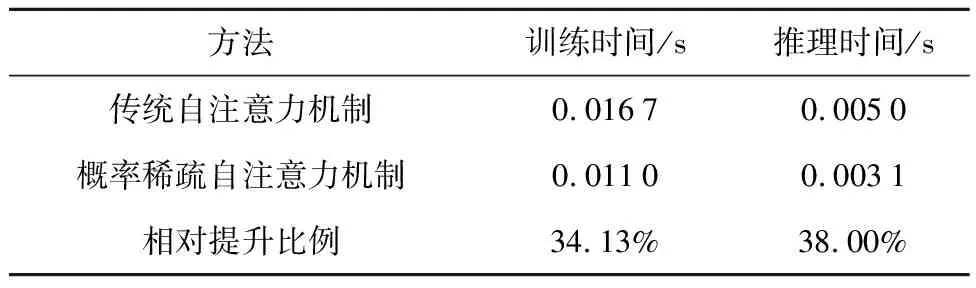
表5 平均计算时间对比Tab.5 Computational speed comparison

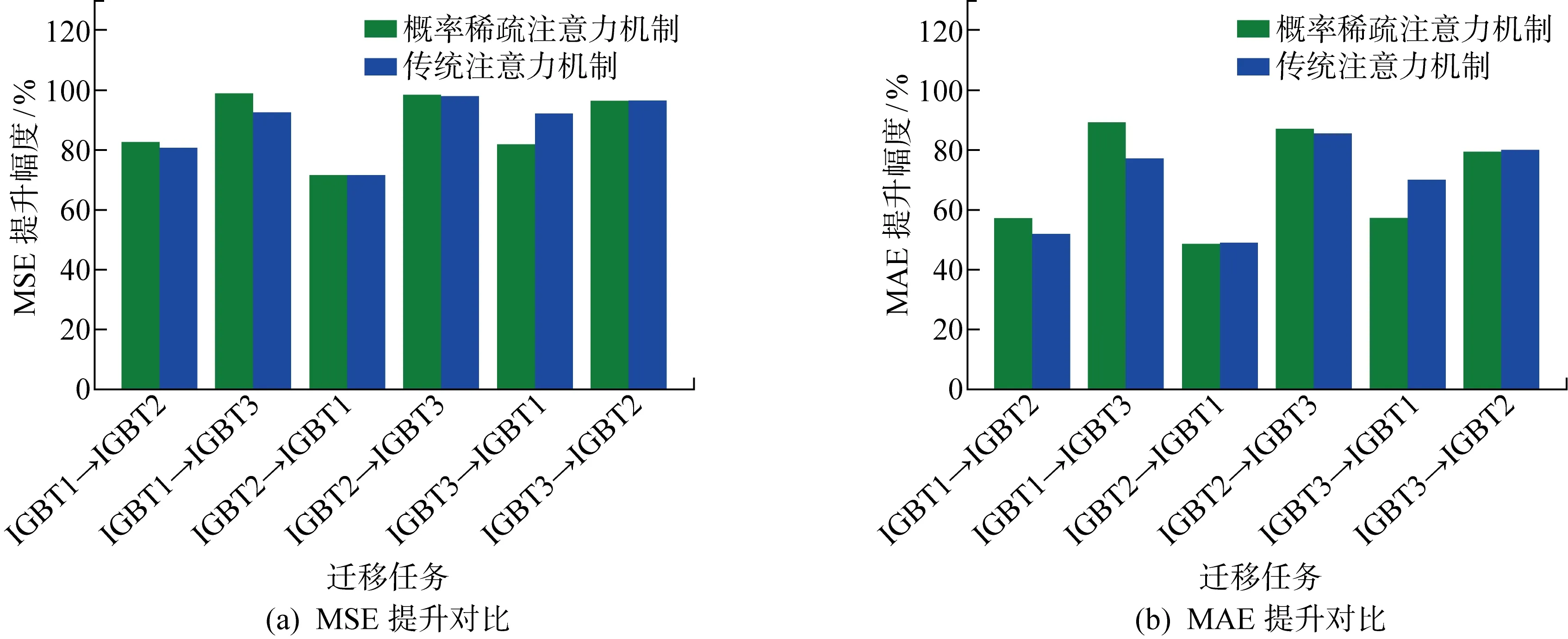
图12 预测性能提升对比Fig.12 Comparison of prediction performance improvement

使用概率稀疏自注意力机制的模型相比使用传统自注意力机制的模型在训练时间和推理时间上都缩短了超过30%,而二者在预测性能上基本相当,MSE提升幅度最大相差不超过10%,MAE提升幅度最大相差不超过13%,因此概率稀疏自注意力机制在大幅提升计算速度的情况下仍保持了优秀的预测性能.

4 结语

为了实现更准确的IGBT剩余寿命预测来提高其可靠性,在不同工况下对IGBT模块进行了加速老化试验,提出了一种基于概率稀疏自注意力机制和迁移学习的方法,利用瞬态热阻在模块衰退过程的变化数据,实现了IGBT模块剩余寿命的跨工况预测.该方法能够减小目标域样本和源域样本深度特征分布的差异,从而在所有迁移任务上达到最优效果,大幅提升了IGBT模块早期衰退过程中的剩余寿命预测精度,同时证明了两个相近工况模型迁移较容易,而两个相差较大的工况,从更严苛的工况迁移到更宽松的工况与反向迁移相比提升更加明显.