组合立管系统内气液两相流特性及管道共振分析
亢嘉颖,王琳,丁超群,李连顺,杨康,向绍宏,徐进杰
1.中国石化胜利油田海洋采油厂;2.西南石油大学机电工程学院
0 引言
气液两相流诱发的管道振动对管道系统的安全性和完整性有很大影响[1]。当立管系统中有气液两相流通过时,流体密度、压力等参数随时间变化,可能引起管道系统的参数共振和组合共振。尤其在上升管路中,两相流流型会剧烈变化,使得通过流型整改来抑制管道振动的方法难以奏效。而立管系统的支承防护和基础设计,需要充分考虑气液两相流与立管系统的耦合振动效应。因此,建立气液两相流立管系统的振动模态分析方法,分析不同流动状态下的振动特性是非常必要的。
与单相流管道相比,管内复杂的两相流特性使得管道振动特性很难预测。因此,很多学者通过实验手段研究了两相流引起的激振力。Riverin 等[2]测量了空气-水混合物在弯管和汇管处产生的时域的流体力,并将这些力与局部测得的含气率进行关联。Liu 等[3]通过试验测试了两相流对弯头的脉动流体力。Gong[4]分析了一例化工厂中蒸汽管路的断裂事故,认为液塞在水平管内加速引起较大瞬态冲击力冲击立管,造成了管道在连接处断裂。Hara[5]对段塞流引起的水平管振动进行了理论研究,并与实验结果进行了对比,结果表明:两相流气液比对管道振动影响较大;当管道固有频率与段塞频率比值为1/2、1/1、3/2…时,管道振动强烈。Pettigrew 等[6-8]对两相流引起振动的机理进行总结,并对两相流横掠管束的振动进行了深入研究。Tay等[9]提出了一个塞状流模型,用来预测水平弯头受到的时域冲击力。另外,一些研究中应用商业软件和计算程序来模拟管内多相流引起的管道系统动力响应[10-11]。管道中气液两相流动的理论特性非常复杂[12-16],即使在管道不振动的情况下都是如此[17]。因此,气液两相流立管系统耦合振动问题仍需进一步研究。
1 实验装置
实际管道空间分布复杂。利用下倾管道和上升管道的组合来简化模拟存在地形起伏的管道系统,可用于研究地形起伏诱发的复杂的两相流流动。利用立管实验装置对气液两相流的流动特性和管道的振动特性进行测试。气液混合物从卧底管道进入,从立管顶部流出,管道系统如图1 所示。
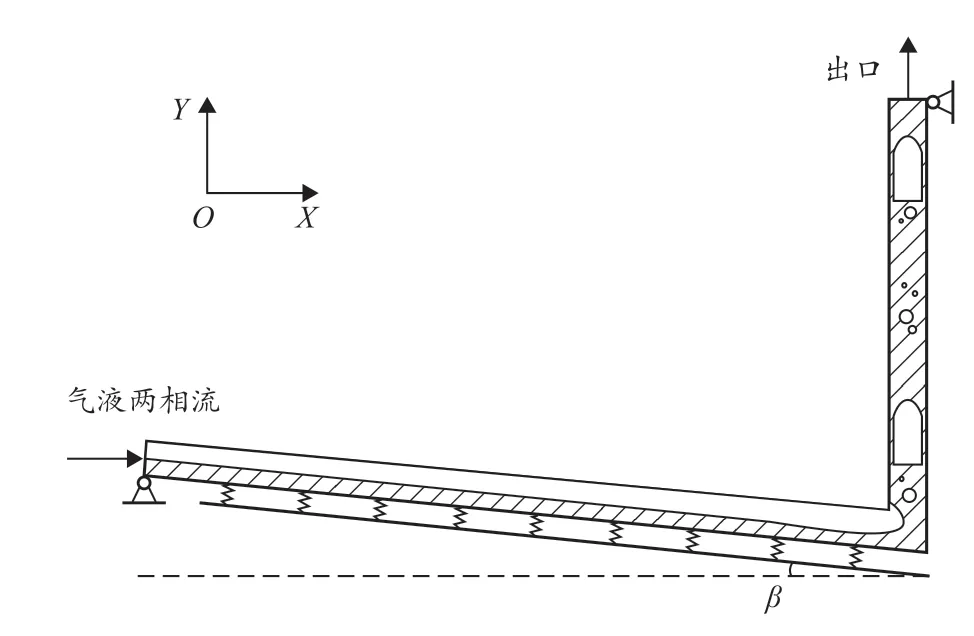
图1 管道系统示意
两相流实验装置的环路主要由一个35 m 长的水平管路和12 m 长的下倾管段及3.5 m 高的垂直上升立管连接而成,其中立管系统由下倾管和垂直管形成的组合立管来模拟。实验装置流程如图2 所示。实验中流体介质为水和空气。水由两个0.5 m3的储水罐提供,其中一个罐也用做环道回水的缓冲罐。液体输送的能量由两个排量为12.5 m3/h,扬程25 m的卧式离心泵提供。两个泵可并联也可串联,可提供压力最大为0.5 MPa。空气由排量为61.5 L/s、工作压力为1.25 MPa 的往复式压缩机提供。压缩机后有一个2 m3的气体缓冲罐用来稳压。气体流量由下游的节流阀控制。立管系统上安装有MPM480 压力变送器,对两相流压力特性进行测试。位移传感器选用米朗®KPM 型直线位移传感器,量程为10 mm,线性精度±0.1%,信号无断解析。下倾管弹性基础的弹性系数为10 000 N/m2。
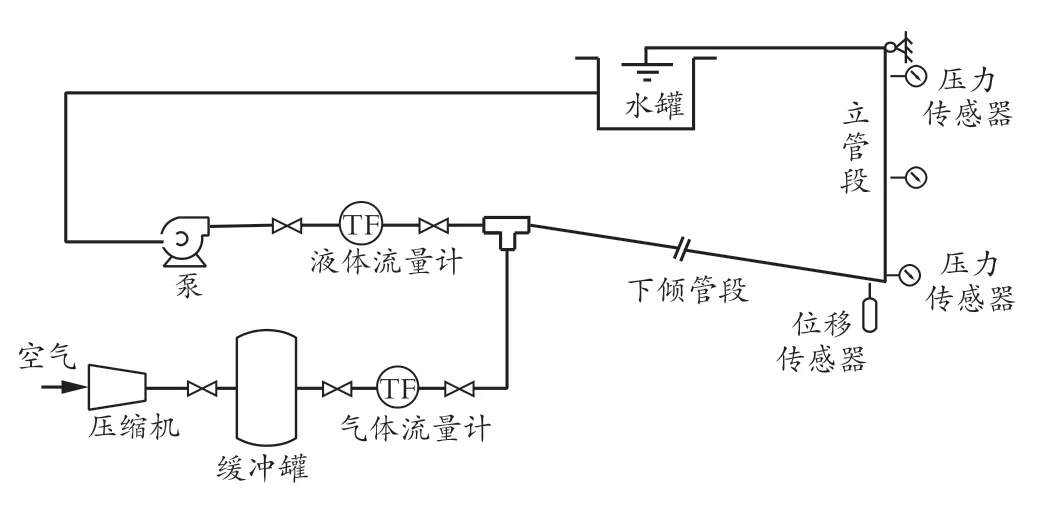
图2 气液两相流立管实验装置流程
2 数学模型
为了避免实验装置与两相流发生共振,通过对实验装置进行模态分析,确定实验装置的约束条件。由于管道的长细比很大,其剪切变形可以忽略,将管道简化成Euler-Bernoulli(欧拉-伯努利)梁模型[18],同时考虑管道的横向和轴向位移。管道单元的广义位移矢量可表示为:
式中:Ue——单元节点位移矢量;uA、vA——A节点的轴向和横向位移,m;θA——A 节点的旋转角,rad;uB、vB——B 节点的轴向和横向位移,m;θB——B 节点的旋转角,rad。
管道单元动力学方程[19]的矩阵形式表示如下:
式中:Me、Ce、Ke——质量、阻尼、刚度矩阵;Pe——单元节点力向量;——单元节点位移矢量的一次、二次导数。
卧底管道的弹性基础可以按Winkler 基础来处理[20],并且考虑管内流体的附加质量,则:
式中:Mes、Mef——管材、管内流体的质量矩阵;ρs——管材密度,㎏/m3;As——管材横截面积,m2;Af——流体通道横截面积,m2;N——形函数矩阵;NT——形函数矩阵的转置;s——沿管道轴向的一维坐标,m;αe——管道单元的平均体积含气率;ρ1——管内流体密度,㎏/m3;l——管道单元长度,m。
式中:Kes、Kew——管道单元结构、弹性基础的刚度矩阵;E——弹性模量,Pa;B——应变矩阵;k——基础的弹性系数,N/m;dA——面积的微分变量。
系统的总体动力学方程可表示为:
式中:M、C、K——总体质量、阻尼和刚度矩阵;U、P——总体节点位移和力向量。
阻尼对固有频率的影响可以忽略,且线性阻尼和低流速对管道的固有频率的影响较小。因此,自由振动频率即管道的固有频率,系统的自由振动方程如下:
此二阶常系数齐次微分方程解的形式为:
式中:ω——管道系统的固有频率,Hz;φ——相对应的位移向量相应的振型。
公式(3)中,管道单元的平均含气率如下:
式中:α——管道单元的局部体积含气率。
局部体积含气率可表示为:
式中:αP、αr——卧底管道、立管内的局部体积含气率。
卧底管道内的体积含气率由Mukherjee-Brill 关联式[21-22]计算,Mukherjee-Brill 关联式如下:
式中:Ngw——气体流速数;NLw——液体流速数;β——管道倾角,°;N1——液体黏度数。王琳等[23]分析了公式(10)中相关变量的数学模型求解方法及验证。
3 结果分析
3.1 流型演化
立管内观察到的流型总体上分为严重段塞流(SS)、第二类严重段塞流(SSII)、过渡流型、稳态流和水力段塞流。
典型严重段塞流出现时的气液流量都很小,流动具有阶段性,可分为4 个阶段:液塞生成、液塞流出、气液喷发和液体回落阶段。各阶段立管内的典型流态如图3(a)~图3(e)所示。液塞生成阶段,下倾管内气液分层流动,液体在立管底部累积,封堵了气体流动通道,使气体在下倾管内聚集,同时,随着液体在立管底部的不断累积,立管内的液位逐渐上升,造成下倾管内静压不断增大,压缩下倾管内的气体,液塞尾部向流动方向相反方向移动。当立管中的液位上升到立管顶部后,立管底部静压不再增大,而此时随着下倾管内气体的逐渐累积,液塞尾部(气液界面)逐渐向立管移动,液塞在立管顶部不断流出,此为液塞出流阶段。当气体空间的压力超过立管内液体的静压力时,气体进入立管,使气体空间的静压突然减小,气体加速膨胀,推动液体加速喷出。喷发阶段结束后,少量液体回落,液体重新在立管底部累积,周期性流动进入下一个循环。典型严重段塞流的典型特征是立管内可以充满液体,立管出口处存在液体断流阶段。

图3 立管内各种流动形态
在严重段塞流的基础上,液体流量继续增大,间歇性的弥散气泡和泰勒气泡进入立管,如图3(f)、图3(g)所示。此时,液塞长度小于立管长度,而卧底管道内呈现分层流,我们将这种流动形态定义为第二类严重段塞流(SSII)[24]。而在严重段塞流基础上,气体流量继续增大,气体将以气团和泰勒气泡的形式不断进入立管,如图3(h)、图3(i)所示。此时卧底管道里面呈分层流。此时,立管内的泰勒气泡更大,含气率更高,立管内流动状态不稳定,且规律性不强。这个区域是严重段塞流向稳定流动过渡的状态[24],因此,称之为过渡流型。
当气体和液体的流量都增高时,两相流动状态趋于稳定,立管内主要体现为气泡流和混状流,如图3(j)、图3(k)所示,此时卧底管道内呈现气团流或者分层流。我们将这种流动状态定义为稳定流动。
当气体和液体的流速都较大时,卧底管道中形成的水力段塞不断流过立管。此时立管内也是水力段塞流,只是形态上与卧底管道中略有不同,如图3(l)、图3(m)、图4(f)、图4(g)所示。

图4 卧底管道内的流动形态
根据不同气液流量下的流型观测结果,绘制流型图如图5 所示,给出了5 种流型所处气液表观流速的范围。
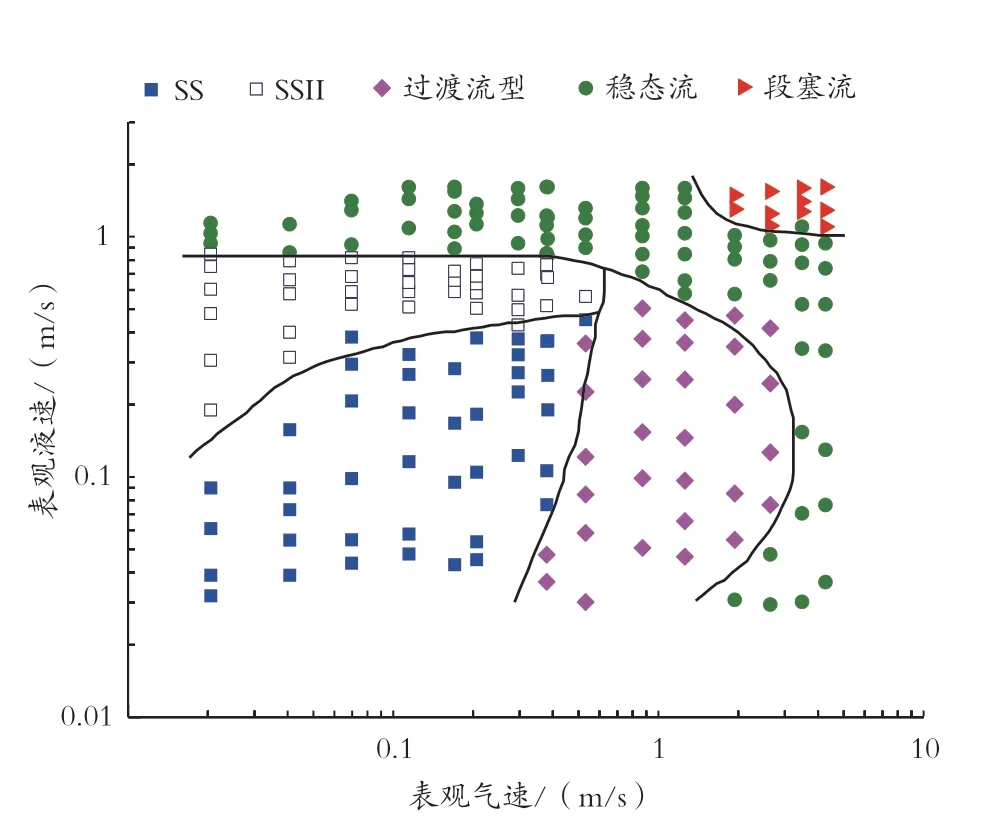
图5 立管内的流型划分
3.2 压力脉动特性
图6 为对管内两相流进行压力测试时3 种工况下的入口条件。“▼”工况下的气体表观流速恒定在0.07 m/s,“■”工况下的液体表观流速恒定在0.60 m/s,“▲”工况下的标况含气率恒定在70%。
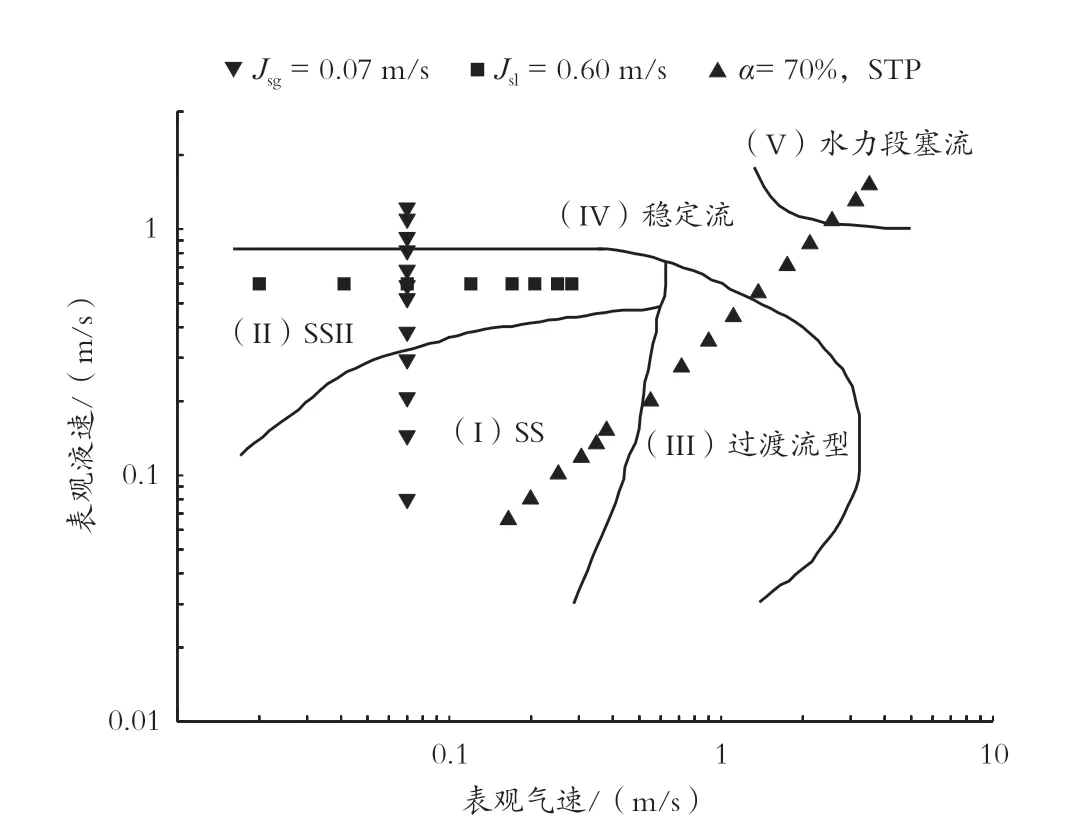
图6 压力脉动测试的入口工况
图7 为气体表观流速恒定在0.07 m/s 时不同液体表观流速下的压力脉动特性。可以看出,立管底部平均压力随液体表观速度线性增长,而压力波动幅值不断减小。图7(c)显示了不同流型的压力频谱,可以看出,严重段塞流在低频段有较大带宽,而第二类严重段塞流在高频段有较小的带宽,另外,稳定流的压力波动非常小。
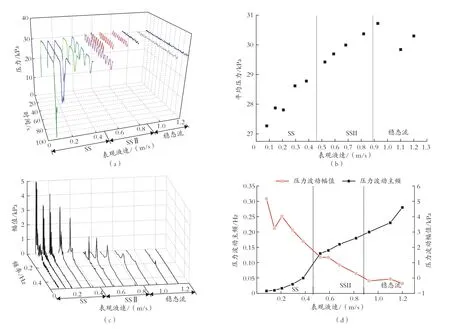
图7 表观气速为0.07 m/s 时的压力脉动特性
图8 为液体表观流速恒定在0.60 m/s 时不同气体表观流速下的压力脉动特性。可以看出,平均压力随气体表观速度线性减小,而压力脉动主频随表观气速的变化非常小,而幅值随表观气速的增大而增大。
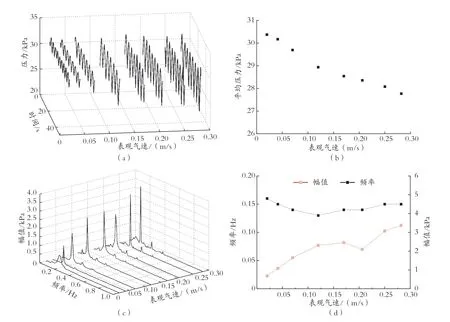
图8 表观液速为0.60 m/s 时的压力脉动特性
图9 为含气率恒定在70%时时不同混合表观速度条件下的压力波动特性。可以看出,过渡流型的平均压力最低,其压力波动频谱在0.14 ~ 0.27 Hz,振幅也较低。而水力段塞流的压力波动幅值较大,主频集中在0.3 Hz,这种显著的压力波动主要是由于长气泡和液塞交替在立管系统内流过。
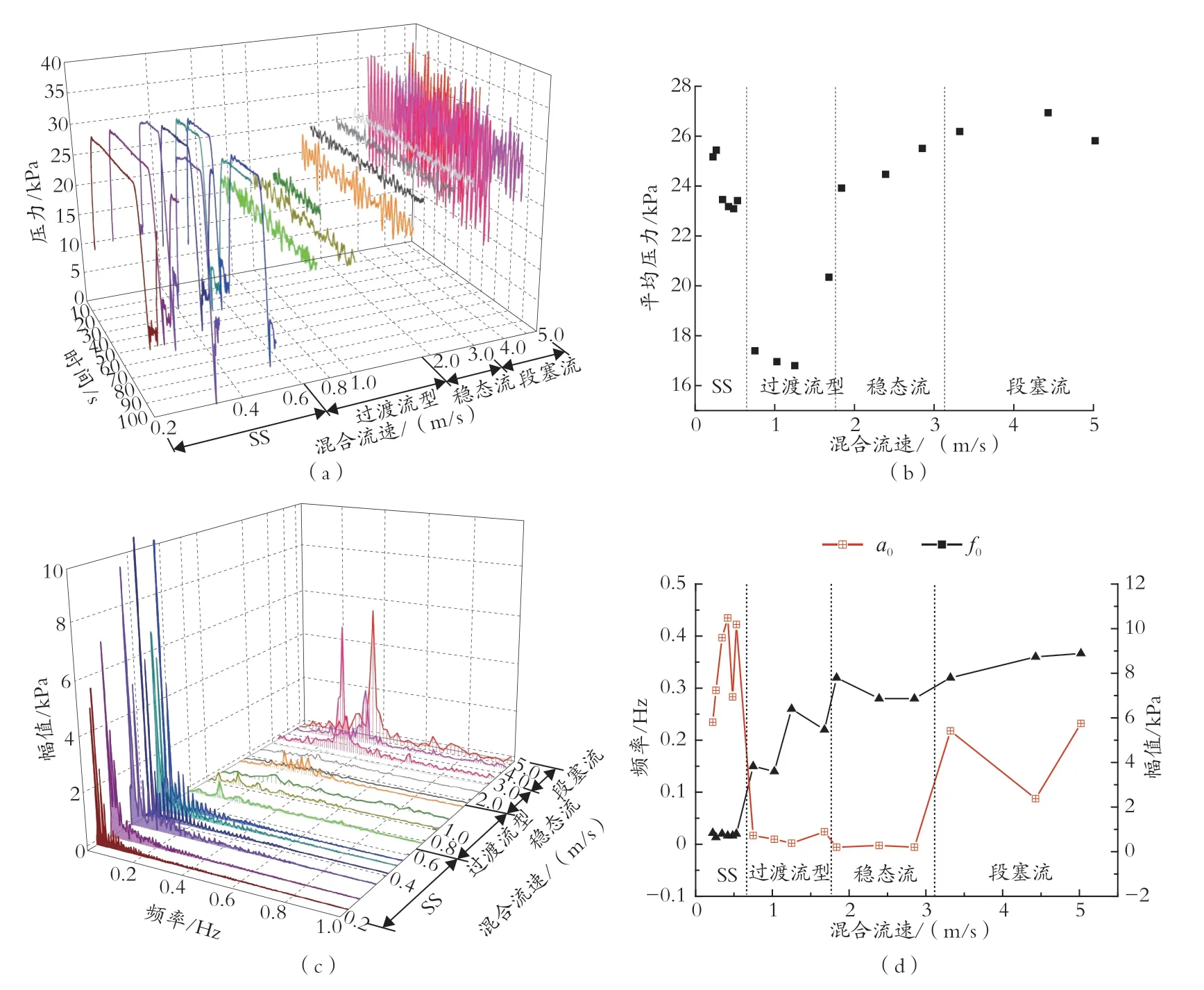
图9 含气率为70%时的压力脉动特性
3.3 含气率对固有特性的影响
图10 不同入口条件下的管内含气率和管道前三阶固有频率。可以看出,较高的入口含气率会使管内含气率也较高,同时对应的固有频率也更高。
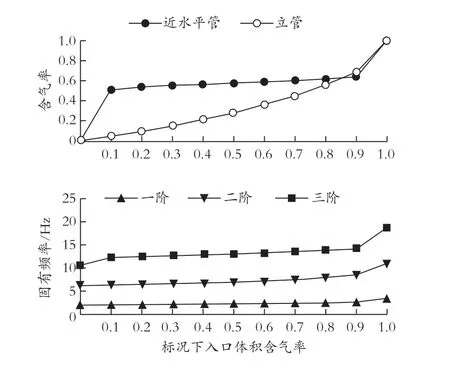
图10 不同入口条件下的管内含气率和管道固有频率
3.4 弹性基础对固有特性的影响
图11 所示为弹性系数为0 ~ 10 000 N/m2之间时的立管系统的固有频率,可以看出,较高的弹性系数会对应较高的固有频率。
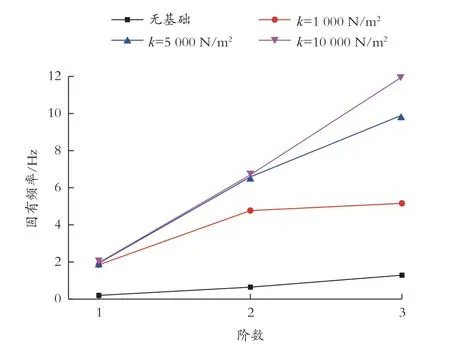
图11 弹性基础对立管系统固有频率的影响
图12 为不同弹性系数下立管系统的前三阶振型。可以看出,弹性系数对振型有很大影响,较大的弹性系数对低阶振动模态有显著的抑制作用。
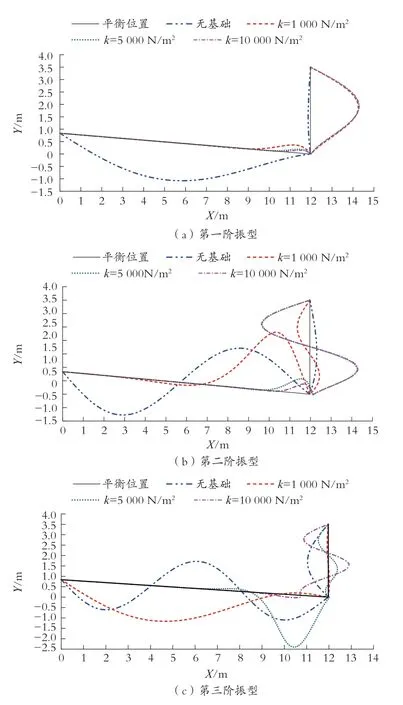
图12 弹性基础对前三阶振型的影响
3.5 共振分析
图13 为各种流型压力波动的幅频特性,包括波动频率和幅值的变化范围。可以看出,严重段塞流,第二类严重段塞流,过渡流型,稳定流动和段塞流的脉动频率依次增大。而严重段塞流和水力段塞流的压力波动幅度比其他几种流型都大。
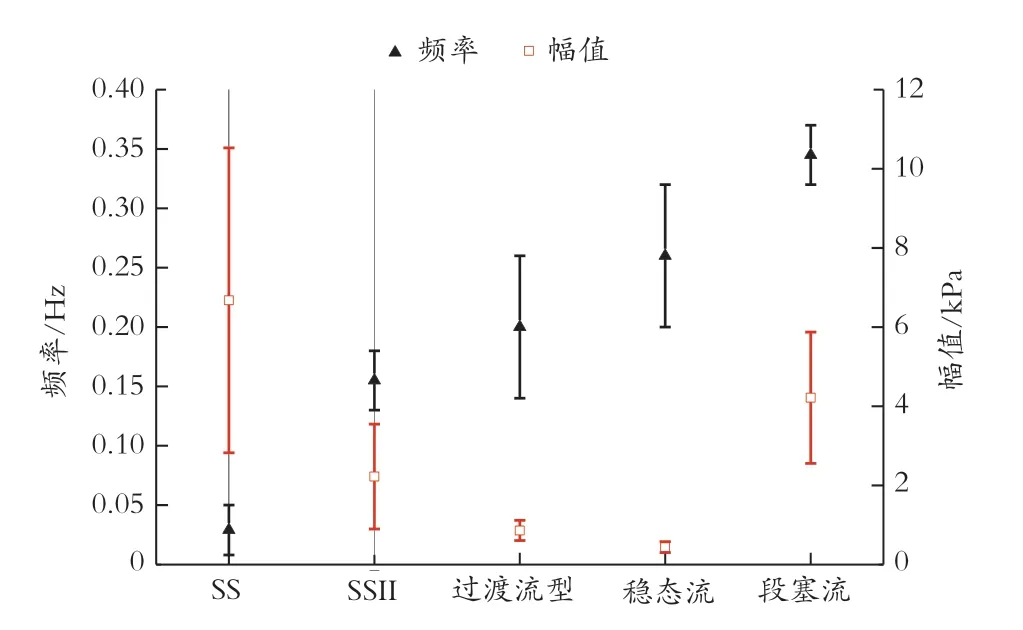
图13 两相流压力波动的幅频特性
图14 为两相流波动主频与管道(无基础)固有频率的对比。可以看出,第二类严重段塞流、过渡流型和稳定流动的波动主频与无基础时的管道系统的基频重叠。这表明,管道系统如果没有基础支撑时,会与这3 种流型共振。而当基础支撑存在时,即便弹性系数较小,管道系统的固有频率也会大大提高,远离共振区。
4 结论
立管中观测到的流型被分为5 类,同时,卧底管道中观察到了段塞流、气团流以及水力段塞流。
立管系统中两相流的压力脉动主要集中在低频,其中严重段塞流、严重段塞流II 及水力段塞流的压力脉动比较剧烈。
立管系统固有频率随管内持液率的升高而降低,随基础弹性系数的升高而升高;气液两相流和基础弹性系数对立管系统的振型影响很大,两个因素共同作用下振型呈非对称性。
严重段塞流和水力段塞流可能引起应力超限和疲劳损伤,因此,应尽可能避免这两种流动形态。

