基于接壤城市数据的居民用气量复合模型及预测

王歌，刘世章，戴松霖

昆仑数智科技有限责任公司

0 引言

随着中国城镇化率的不断提升，以及“碳达峰、碳中和”目标的提出，作为清洁能源，天然气在能源消费中的占比快速增加。国家能源局发布的《中国天然气发展报告（2021）》显示，2020 年全国天然气消费量同比增长6.9%，从消费结构看，城市燃气同比增长10.5%，占比32%［1］。其中，根据国家统计局公布的数据，2020 年居民生活天然气消费总量为560×108m3，同比增长11.5%。可以预见的是，未来随着城市燃气的发展和“煤改气”逐步推进，居民用天然气的市场份额将不断扩大。作为城市燃气中的基础，居民用气的稳定供应关乎百姓民生。然而，近年来供暖季“气荒”现象却频频出现，利用历史数据对居民用气规模进行准确预测，以实现对天然气资源采购、管网铺设及市场销售的合理规划，成为当下亟待解决的问题。

目前对于居民用天然气需求预测的研究按照时间跨度可分为短期、中期、长期预测3 种：短期预测通常是预测未来一周、一天或者一小时的负荷，以对天然气短时间内的使用情况提供理论依据，实现资源的合理调配；中期预测一般是以月或者季度为单位进行预测，为决策者合理安排计划、进行人员调动、设备维修维护等提供指导；长期预测通常以年为单位，通过对宏观数据的预测，为城市提供管道建设的理论依据［2］。在模型选择上，既有时间序列模型、回归模型、灰色预测、不均匀系数等传统预测模型，也有为处理大规模数据中所蕴含的规律而使用的SVM（支持向量机）、小波分析、神经网络等深度学习模型，还有由此衍生出的用以提升预测精度的组合模型，包括对组合中各预测方法加权平均、多个模型结果取最优、将一个模型的输出结果作为另一个模型的输入等组合方式。

针对不同类型的天然气需求预测，学者们选择了不同的数学模型对其进行预测。胡凯［3］利用2015—2018 年合肥燃气公司的季度数据拟合Holt-Winter 加法模型实现了对燃气负荷的季度预测，最终将模型的预测误差控制在10% 以内。武海琴［4］在对北方某城市的冬季用气数据进行分析后，建立了居民用气负荷与日均气温的回归模型，得到较好的预测效果。张超等［5］使用支持向量机建立以气候因素为主要因素的预测模型，最终预测结果与实际值误差在2% 左右。在组合预测上，舒漫［6］利用成都市天然气日负荷数据及季度负荷数据，建立了XGBoost（eXtreme Gradient Boosting，极端 梯度提升）预测模型，将预测平均绝对百分比误差降至2.1%。

通过以上文献的梳理可以看到，以往对居民用天然气需求的预测研究，更多的是基于目标城市的居民用天然气消费数据，通过拟合模型实现对未来需求的预测，但是该类方法不能对无法获取历史数据的城市进行预测。因此，考虑到同省份地域接壤城市在居民用气习惯、天然气市场份额、管网规划等方面往往具有相似性，本文拟使用同省份与目标城市接壤城市的宏观统计数据和历史用气数据，利用回归分析和随机森林模型相结合的方式，建立居民用气需求预测模型，提升模型的可解释性与准确度，实现对无法获取历史数据的城市居民用天然气需求量的准确预测。本文所预测的居民用气数据颗粒度为城市居民用气量的月度值。

1 模型设计

1.1 模型设计思路

在实际的预测研究中，常常会遇到研究对象历史数据无法取得的情况，如在天然气新建管网时期，就需要在缺乏可参考数据的情况下对目标城市用气量进行合理预测。由于邻近城市的政策与经济发展状况相似、人口基数接近、生活习惯类似、气候相近，因此本文借鉴Chong 等［7］、张璇等［8］的思路，使用与目标城市接壤的地级市数据进行模型的拟合。具体而言，在选择用于建模的城市时，主要考虑以下两方面：一是要综合考虑目标城市所属省份各城市的地理位置情况，选择与目标城市接壤的城市，例如对于内陆城市，则应在保证数据质量的情况下尽可能选择同样为内陆城市的接壤城市；二是考虑到接壤城市的历史数据应具有一定规模且用户用气情况稳定，因此本文以同省份各城市用户数量的中位数为标准，在符合条件的接壤城市中选择用户数量在中位数以上的城市。

而在预测模型的选择上，本文使用回归分析与随机森林模型相结合的组合预测方式，具体流程如下：

1）本文的研究对象是无法获取历史数据的城市，在变量选取上考虑与接壤城市有共通性的宏观变量，并采用定性与定量相结合的方式，即先根据过往研究成果及接壤城市与目标城市的现状，定性居民用天然气消费量的影响因素，而后使用回归分析，定量确定影响需求预测的变量。

2）将选定的变量传入随机森林模型，利用接壤城市数据构建居民用气量的预测模型，并以此来预测目标城市的居民天然气用量。其中，随机森林建模过程如下：①读入接壤城市数据，并确定随机森林模型中要进行调参的参数，以使模型有更准确地预测效果。本文选取了决策树个数、最大深度、最小分离样本数（拆分决策树的节点要求的最小样本数）、最小叶子节点样本数（每个叶节点需要包含的最小样本数）、最大分离特征数（寻找最佳节点分割时要考虑的特征变量数量）等5 个参数，并在模型训练过程中对各参数的范围进行划定，初步确定参数的最佳范围。②在划定的范围之内，使用随机搜索（Randomized Search CV）的方式，将需要调参的各参数进行匹配，确定最佳的取值组合。为防止此时的最佳组合只是局部最优而非全局最优组合，需在最佳组合的临近范围内重新划定各参数的取值范围并进行网格搜索，通过多次循环此步骤找到最佳的参数组合。③使用②中的参数组合即可得到最终的随机森林预测模型。

相比于以往的模型，此预测方法的优点在于：一是回归分析和随机森林模型均适用于中长期预测［9］，若单独使用回归模型，则无法很好地应对冬季供暖期天然气用量大幅上升的情况，而随机森林模型可以随机选择样本与特征构建多个决策树，既提升了对冬季数据的拟合能力，也能很好地减弱过拟合的发生，同时还具有很好的鲁棒性；二是虽然随机森林有利于提升模型预测准确度，但在模型解释性上表现较差，回归分析则可以很好地弥补这一点。

1.2 预测流程

基于上述模型设计思路，本文的预测流程见图1。

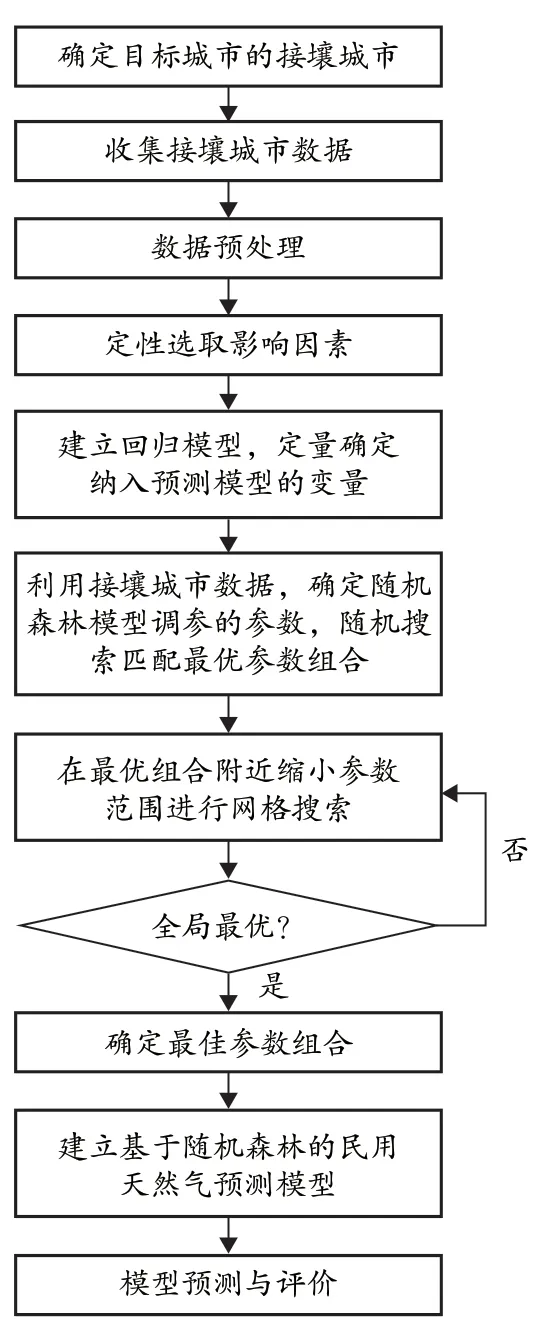
图1 预测流程图

2 数据来源与数据处理

本文以北方某省份为研究对象，所使用的城市居民用气量数据来自某天然气公司的终端销售数据。该数据均为物联网远传表数据，每日定时上传用户当日用气情况，可以真实反映各市的民用天然气消费情况。考虑到用于研究的数据应处于各市的成熟用气阶段，因此本文选取的建模数据时间范围为2020—2022 年。

本文所使用的宏观经济数据，是由该省份各城市统计局官方网站上公布的统计月报整理所得，并根据该省份统计年鉴［10-11］进行修正。

在城市的选择上，本文以该省份L 市作为目标城市，预测其2021—2022 年居民用气情况。同时，选择在2022 年12 月1 日零时，居民用户数量在3 万以上的3 个城市——H 市、J市、A 市为L 市的接壤城市，使用这3 个城市的相关数据构建预测模型。

为提高样本数据的代表性，本文对所使用的数据进行如下处理：①由于原始数据为各城市居民用户的日用气量（远传表上传），需要对居民日用气量进行分月加总，得到各城市的月度用气量；②由于在远传表试运行阶段，用户规模及用气量有时会偏离正常值，有时也会存在数据冲正等情况，所以用气数据在其数据分布曲线的两端均存在较多异常值，因此对接壤城市数据进行双侧10%的截尾处理（将大于90%分位数或小于10%分位数的取值替换为缺失值），以消除异常值对模型的干扰；③由于各城市的经济收入数据为季度数据、人口数据为年度数据，考虑到这些数据在一定时间内具有相对稳定性，因此对其进行均值插补，即对于经济数据，季度内各月取季度均值，对于人口数据，年内各月取年度均值；④由于各变量数据的数量级相差较大，因此使用Z-Score（标准分数，将一个数与平均数的差再除以标准差，见公式（1））对各变量的数据进行标准化处理，以使模型在训练时能够更快的收敛到最优解。

式中：Z——标准分数；X——原始数据；——平均数；s——标准差。

图2 为处理后的接壤城市各月用气量数据。

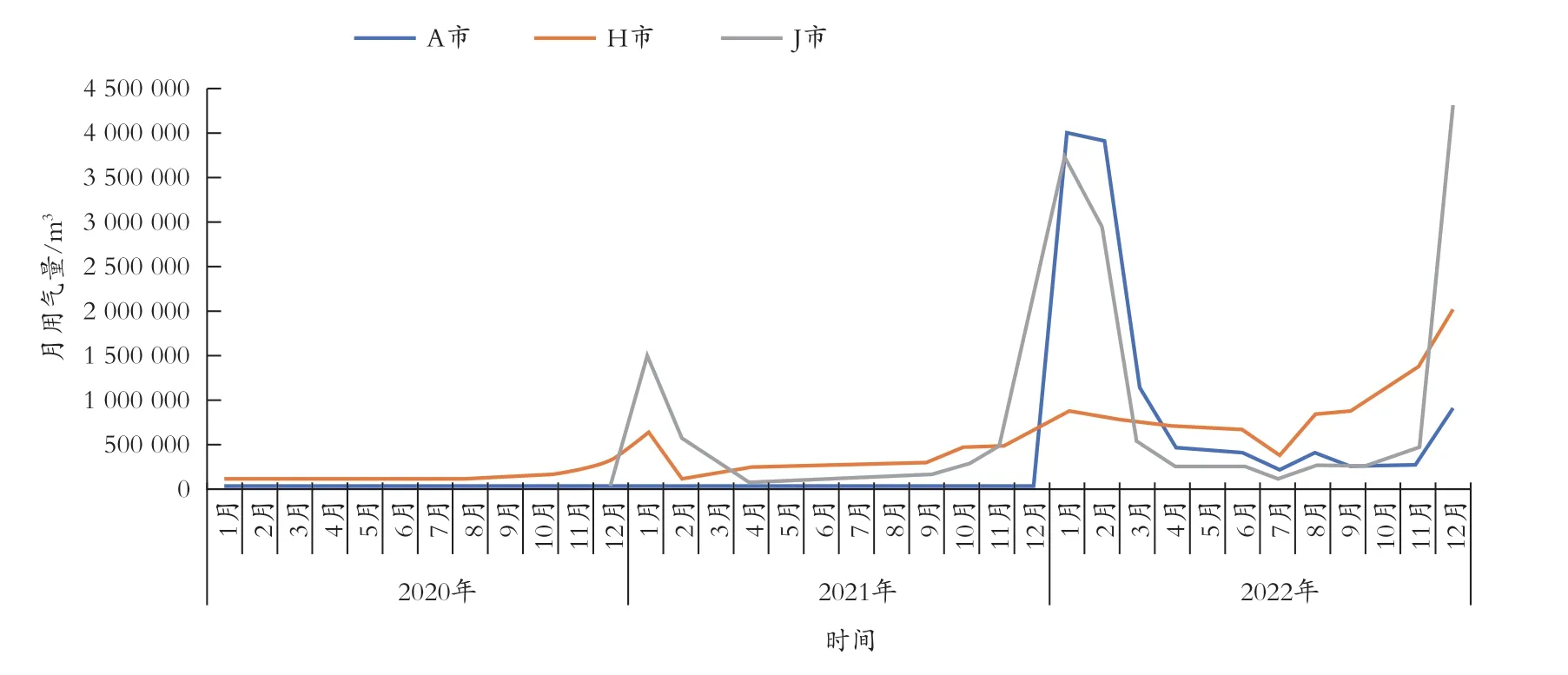
图2 接壤城市各月用气量

表1 为各城市居民月度用气量的描述性统计值，其中用气量一栏为截尾处理前的原始数据，Q为截尾处理后的用气量数据，由于目标城市为预测对象，因此没有截尾数据，只报告原始数据情况。从表1可以看到用气量数据的整体分布情况。原始用气量数据的离群值较多，最大值与最小值相差很大，右侧拖尾严重，同时中位数远小于均值，呈现右偏分布。在进行截尾处理后，变量Q的均值与中位数更接近，说明对其进行10%的截尾处理是合适的。

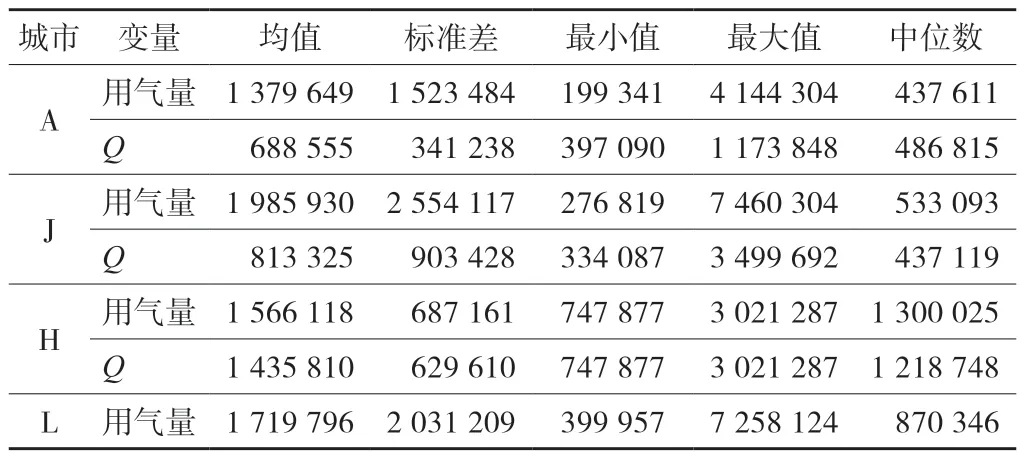
表1 各城市居民月度用气量描述统计信息 单位：m3

3 变量选取

3.1 定性选取影响因素

影响居民天然气使用量的因素复杂多样，鉴于利用接壤城市对无法获取历史数据城市的居民用气量进行预测，因此本文聚焦于宏观因素对用气量的影响。一般而言，影响居民用气量的宏观因素主要有4 个方面。

3.1.1 经济因素

城市的整体经济状况一方面决定着该市居民的收入水平，居民的可支配收入越高，消费意愿越高；另一方面也会对周围城市产生虹吸效应，使该城市的人口维持较高水平的增长。赵立春［12］研究认为，人均可支配收入对高收入和低收入居民的用气量均有较大影响，其中对高收入群体的影响更显著，但这个增长关系并不会一直上升，而是在达到一定程度后保持相对稳定。同时，由于商业的繁荣程度影响着居民的生活质量和水平，因此第三产业与民用天然气用量也有着此消彼长的关系。王钦等［13］通过构建青岛市内四区用气量与第三产业GDP 的一元高次方程，实现了对商业用气量的较好拟合。

3.1.2 人口因素

城市的人口数量及结构决定着民用天然气消费量。城市人口数量越多，民用天然气消费量也越大。对于居民而言，每个家庭人口越多、家庭中老年人占比越大，用户的用气量也会越大。赵立春［12］通过对北京居民进行问卷调查，提出每个家庭人口数、家庭成员年龄结构都不同程度影响着天然气消费量。

3.1.3 气候因素

气候因素主要包括温度、湿度、降雨量、降雪量等。由于用户在不同季节的用气习惯不同，导致温度是对民用天然气用量影响最大的因素。何恒根［14］通过对天气、日最高温、日最低温、日平均温度、风级、湿度等因素与GDP、人口等因素进行主成分分析，实现对城市天然气需求的短期预测。另外，不同温度附近，温度梯度的变化也不同。陈进殿等［15］提出，天然气日负荷的温度梯度在不同地区、不同温度节点处差别较大，在调峰时要关注日负荷温度梯度较大的省市。

3.1.4 其他影响因素

除了以上提及的因素以外，还有许多随机性的外部因素会对居民用气量产生影响。如政府出台的环保法规以及对天然气的扶持政策，燃气公司对天然气价格的不定期调整，以及节假日、冬季采暖等。

因此，本文综合前人的研究以及统计数据的可得性，在模型的变量选择上主要考虑城市的经济、人口、气候等3 方面因素。

3.2 定量确定模型变量

3.2.1 回归模型构建

根据3.1 中选取的前3 方面因素，结合各城市公布的月度统计指标，进一步将各影响因素选取的变量缩小为以下几个：经济因素使用第三产业GDP描绘城市发展状况，同时选取城镇人均可支配收入描绘居民收入情况；人口因素选择城镇常住人口；气候因素选择月均气温。除此以外，本文借鉴严铭卿［2］和王钦等［13］的研究，加入第三产业GDP 的二次项，并构建如下回归模型来定量衡量各自变量是否对用气量有显著影响，以确定用于构建随机森林模型的变量：

式中：Qi——i城市居民的月用气量，m3；Gi——i城市的第三产业GDP，108元；Ii——i城市居民的城镇人均可支配收入，元/人；Pi——i城市城镇常住人口 ，104人；Ti——i城市的月平均气温，℃；β0——模型的常数项；β1～ β5——各变量的回归系数；εi——随机误差项，它包括除模型中各自变量以外影响用气量Q的其他因素。

3.2.2 回归结果分析

利用三个接壤城市数据，建立式（3）的回归模型，本文在回归时使用稳健标准误差以修正模型中可能存在的异方差，使模型显著性结果更稳健。

式中：Q——居民月用气量，m3；G——第三产业GDP，108元；I——居民城镇人均可支配收入，元/人；P——城镇常住人口，104人；T——月平均气温，℃。

模型结果见表2。可以看出，各变量的系数均在1%的水平上显著，说明各变量均对居民的用气规模有显著影响，可以用于建立随机森林模型。

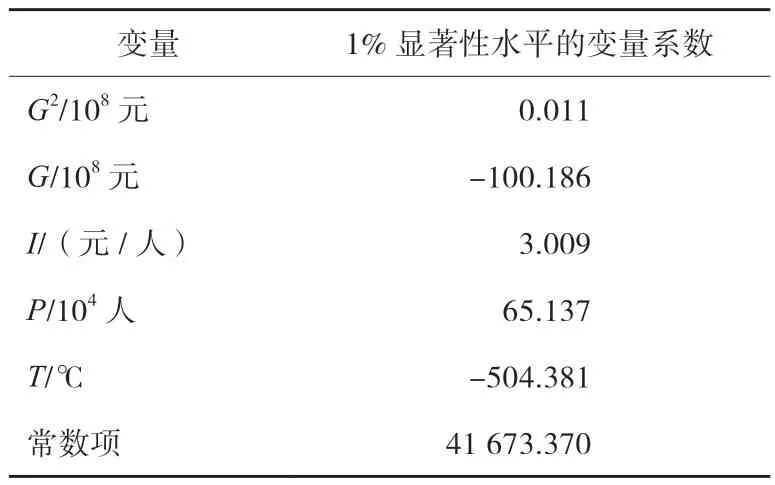
表2 回归模型1%显著性水平下系数

虽然本文中回归模型旨在验证各变量对城市用气规模的影响，但系数的正负与数值大小也在一定程度上反映了各变量对用气规模的影响方向及程度，为模型提供了解释性。分系数来看，G2系数为正，G的系数为负，说明在第三产业发展初期，对居民用气量存在抑制作用，但随着第三产业的不断发展，其促进作用大于抑制作用，这可能是由于经济的发展带来的虹吸效应，吸引了更多的人口聚集到该区域，使其对居民用气量的促进作用超过了抑制作用；I系数显著为正，表明其他条件不变的情况下，随着经济的发展和收入的不断提高，民用天然气消费量也在不断提高；P系数为正，符合预期，说明人口数越多，天然气用量越大；T系数也与预期相符，在其他变量保持不变时，月平均气温每提高1度居民用气规模降低504 m3，表明温度越低，居民天然气用量越大。因此，当季节变换时，要及时调整天然气供应，保证居民用气需求。

3.2.3 回归稳健性检验

为验证上文回归结果的稳健性，本文采用替换自变量的方法进行稳健性检验，将第三产业GDP 及其平方项用GDP 及其平方项替换，并进行回归检验，回归结果见表3，可以看到各变量回归系数依然是显著的。说明前文回归分析模型中，各变量对用气量均有显著影响，验证了回归分析结果的可靠性，可以利用回归模型中的自变量建立随机森林的预测模型。

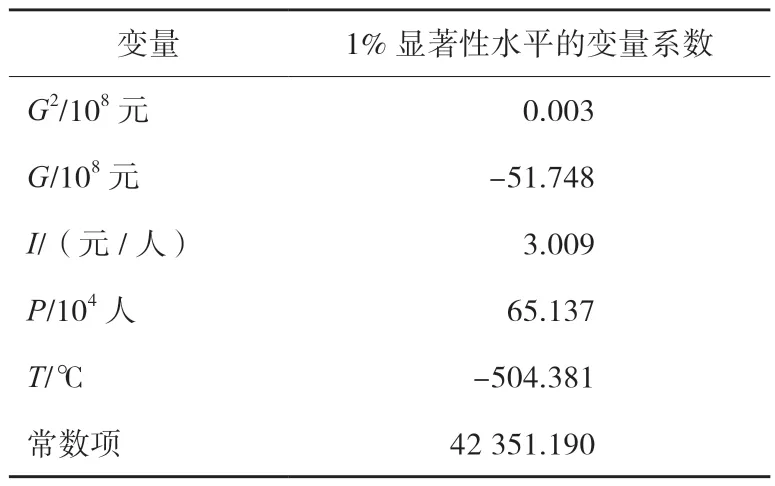
表3 更换变量的稳健性检验结果

4 建模、预测与评价

4.1 模型构建与预测

利用回归分析的结果，将选取的变量作为随机森林模型的输入变量，使用接壤城市数据，利用python 进行随机森林模型构建，根据1.1 中所选择的调参参数，设定各参数的初始取值范围见表4。

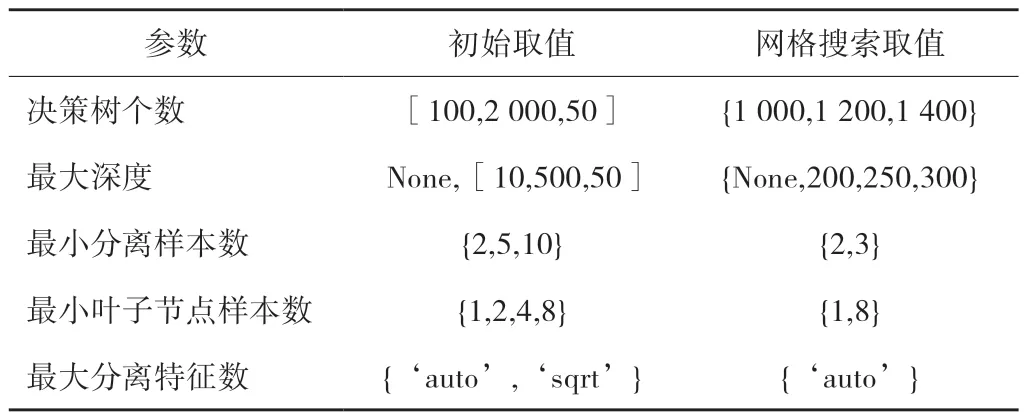
表4 随机森林模型各参数取值

表4 中，决策树个数从100 至2 000，取值间隔为50；最大深度取值不限，或从10 至500，取值间隔为50；最大分离特征数取“auto”（即分枝时考虑的特征个数最大等于决策树个数）或“sqrt”（即分枝时考虑的特征个数最大等于决策树个数的平方根）。

根据初始范围，使用3 折交叉验证与随机搜索（即随机匹配超参数组合，不对所有组合遍历，本文设置匹配200 次）的方式优化参数，得到最优组合，但由于是随机搜索，因此为防止此最优组合为局部最优，在最优值附近划定范围，使用网格搜索对每一种匹配进行遍历，最终得到的随机森林模型各参数取值见表5。

表5 用于预测的随机森林模型各参数取值

根据L 市统计数据，使用上文建立的随机森林模型对接壤城市和L 市2021—2022 年的居民用气规模进行预测。同时，由于在天然气需求的研究中，SVM、XGBoost 也是经常用到的模型，其中既有用于短期预测的研究［5,6,16-17］，也有用于中长期预测的研究［6,18］，因此本文将随机森林的预测结果与SVM、XGBoost 的预测结果进行对比，接壤城市预测结果及目标城市预测结果分别见图3 和图4。

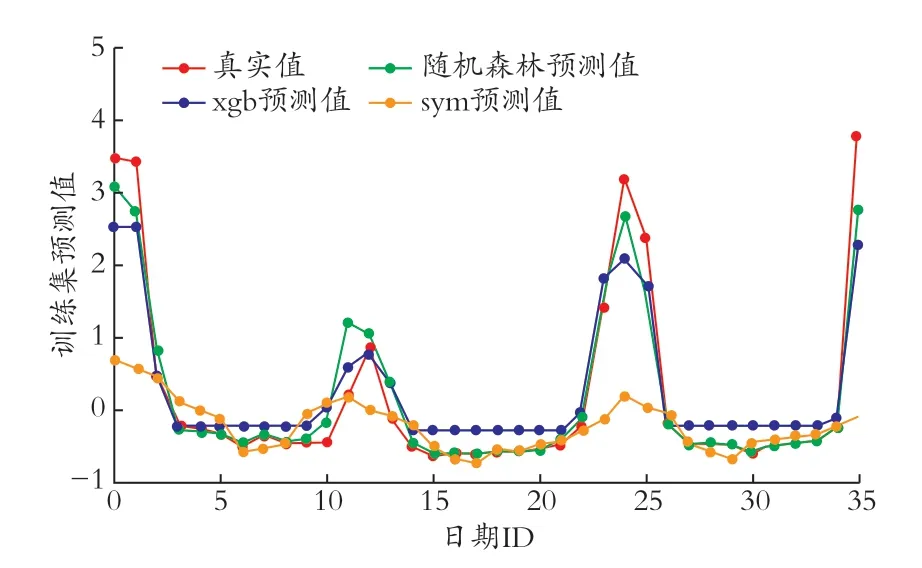
图3 接壤城市训练集各模型预测结果对比

图4 目标城市测试集各模型预测结果对比

其中，由于在建模前对数据进行了标准化，因此纵轴会存在负值，横轴代表日期ID（将2020 年1 月记为0，2020 年2 月为1，以此类推）。可以看到，随机森林较为准确的预测了全年的用气情况，而XGBoost 只追踪到了较高用气量的情况，SVM 则正相反，只能拟合用气量较低的春夏季。

此外，还要对建立的模型进行变量重要性分析，用以确定各变量在建立决策树及划分节点时的重要程度（结果见图5）。在建立模型的过程中，温度是最为重要的影响因素，与回归分析中得到的结论相互印证。主要是短时间内人口、经济状况、收入等因素往往较为稳定，但当跨年度进行预测时，这些变量的作用就会显现。

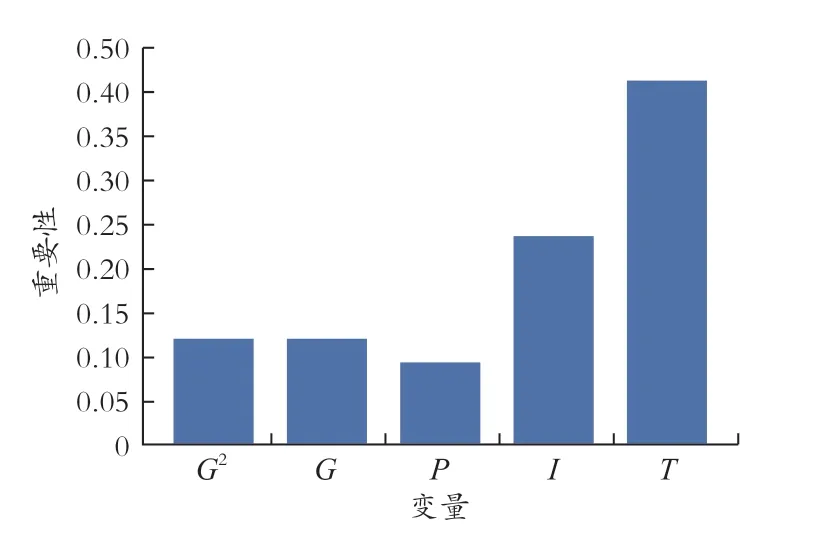
图5 变量重要性分析

4.2 模型评价

本文使用均方误差、模型拟合优度两项指标来衡量随机森林、SVM、XGBoost 模型以及3.2 节中构建的回归模型的预测效果。

式中：RMSE——均方误差；R2——模型拟合优度；yi——用气量真实值，m3；——用气量预测值，m3；——用气量的均值，m3。

以上评价指标均使用目标城市数据计算（结果见表6），可以看到相比于其他模型，随机森林的预测效果最好，RMSE仅为6.4%，这一结果与图4 预测结果对比图中的数值也相吻合。

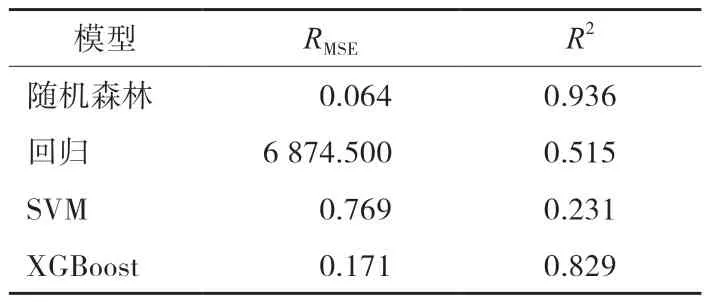
表6 各模型预测效果对比

5 结论与建议

本文针对目标城市无法获取居民历史用气量数据的情况，利用北方某省份2020—2022 年的居民用气数据，结合与目标城市接壤的城市统计月报及所在省份统计年鉴数据，建立了居民用气规模的随机森林预测模型，并与回归模型、SVM、XGBoost 等模型的预测效果进行对比。实证结果表明，通过定性与定量相结合的方式选取模型变量，不仅为机器学习预测模型的变量选取提供了理论及技术依据，同时也为模型提供了可解释性。此外，相比于其他模型，随机森林模型预测的均方误差仅为6.4%，取得了更好的预测效果，能够实现对目标城市各月用气波动的准确预测。

在实际应用中，应根据各城市的用户数量，合理划定用于构建模型的城市范围，尽可能增大用于建模的样本数量，以使模型更好的挖掘其中的规律。另一方面，可根据当地实际公布的统计指标对选取的变量进行灵活调整，实现更好的预测效果。