基于椭圆轮廓模型的重叠烟叶分级方法*

王臣毅 王艺斌 张 滔 张志华 李昀欣

（1.南京理工大学 南京 210094）

（2.南京焦耳科技有限责任公司 南京 210018）

（3.常德市烟草专卖局 常德 415000）

（4.云南烟叶复烤有限责任公司 昆明 650032）

1 引言

烟草是重要的经济作物，在我国的国民经济收入中占有重要的地位，烟叶分级的目的是对烟叶内在质量进行优劣等级划分，以便充分发挥农业资源的作用，以质论价。而内在质量往往是看不见、摸不着的东西，因而只能通过烟叶所表现出来的外观特征确定烟叶的等级。传统的分级方式通常是人工的眼看和手摸去识别，同时对于从业人员有着一定经验的要求，有着较强的主观性的同时，其效率也较低［1］。随着计算机视觉技术的发展，基于视觉的自动烟叶分级技术也在不断的产生，目前大多数学者采用的方法为人工提取特征加单分类器方法设计分级系统，但仍然存在准确率较低的问题［2～3］，并且没有考虑到实际生产中会遇到多片烟叶重叠的问题。为此本文首先提出了一种联合利用纹理、颜色和形状特征提取，并使用集成学习分级的单片烟叶分级方法。进一步，针对重叠烟叶，提出了一种基于椭圆轮廓模型的烟叶分割算法，提升了重叠烟叶的分离准确性，并使用集成分级方法对分割后的单片烟叶逐片分级。多组真实烟叶数据集上的实验证明，本文提出方法在单片烟叶方法优于现有方法，能有效地对重叠烟叶实施分级。

2 单片烟叶分级

2.1 图像预处理

本文使用纹理、颜色和形状特征结合机器学习方法进行分类，数据集单幅图片大小为4096×8000，图片样例如下。

2.2 烟叶纹理特征

纹理指的是图像像素的灰度或颜色的某种变化，其具有周期性和不依赖亮度和颜色本身这两种特点，而纹理特征就是从图像中计算出来的一个值，对区域内部灰度级变化的特征进行量化。

传统的纹理特征有灰度共生矩阵［4～5］、Tamura［6］特征、LBP 特征等特征，在这里我们使用较为常用的LBP 特征（Local Binary Pattern，局部二值模式），它是一种用来描述图像局部纹理特征的算子，具有旋转不变性和灰度不变性等显著的优点。

实验中分别将图片划分为单区域、双区域和四区域进行特征提取。

2.3 烟叶颜色特征

传统的图片颜色是用每个像素的RGB 值来代表一个像素的颜色，但RGB 这种表示方式容易受到光照的影响，鲁棒性不强。故本文使用HSV 特征［7］。HSV 不受光照影响，具有鲁棒性等优点。HSV 分别代表色调，饱和度，明度。HSV 对光照变化具有较好的鲁棒性。

2.4 烟叶形状特征

形状特征也是能描述一个图片的重要特征，常用的形状特征有描述形状区域的表示特征：面积、周长、分散度、伸长度等，和描述形状边界的表示特征：长度、直径、傅里叶描述子等。其中傅里叶描述子是将轮廓点进行傅里叶变化，从任意轮廓点(x0，y0)出发，按逆时针方向在轮廓上搜索时会遇到(x0，y0)，(x1，y1)…，(xK-1，yK-1) ，则对每个坐标对有可以表示为

傅里叶描述子进行归一化后有很好的旋转不变性和尺寸不变性。同时，对于一幅图像，只需要少量的描述子即可描述大体边界信息，只会丢失细节部分［8］。

本实验选择了周长、面积、分散度和前50 个傅里叶描述子作为特征，共53维特征。

2.5 集成学习介绍

集成学习是使用一系列学习器进行学习，并使用某种规则把各个学习结果进行整合从而获得比单个学习器更好的学习效果的一种机器学习方法。在机器学习的有监督学习算法中，我们的目标是学习出一个稳定的且在各个方面表现都较好的模型，但实际情况往往不这么理想，有时我们只能得到多个有偏好的模型（弱监督模型，在某些方面表现的比较好）。集成学习就是组合这里的多个弱监督模型以期得到一个更好更全面的强监督模型，集成学习潜在的思想是即便某一个弱分类器得到了错误的预测，其他的弱分类器也可以将错误纠正回来。

常用的集成学习方法有Bagging、Boosting 和Voting。其中Voting 分为Hard Voting 与Soft Voting两类，Hard Voting 是一种投票的方式，严格遵守一种少数服从多数的思想。而Soft Voting 则认为有时候少数服从多数并不合理，它将计算得出不同分类器的分类概率均值，选择均值最高的作为预测的结果。本实验中分别构造逻辑回归、决策树和SVM三种分类器，并用Hard Voting 方式对三种分类器集成得到一个新的强分类器。

3 重叠烟叶分级

3.1 重叠烟叶分割预处理

由于在实际生产过程中烟叶并不是标准的单片分开的情况，而是多片混合叠加在一起的复杂情况。故要想将之前所做算法模型应用到实际生产中，必须先解决烟叶重叠的问题。本文先解决如何判断是否为重叠烟叶，然后提出了基于颜色类间方差OTSU 和基于椭圆轮廓的两种烟叶分割方法，对两片烟叶重叠情况进行了分割最终得到单片烟叶后进行分级，整个过程的流程如下。

首先是预处理判断工作，在进行分割前先对图片进行判断，若是图片只属于一片烟叶或者是两片烟叶重合率太高，直接进行分类而不用先进行分割。

单片与重叠的判断是一个典型的二分类问题，除直观的面积和周长外，还选取了凹点比例和叶柄数，一共四个特征。

可以看到如图5，两个烟叶重叠时会形成凹点，凹点的个数越多则是两片烟叶重叠的情况可能性越大。

凹点的寻找方法有很多［9～12］，这里采用计算圆形模板面积的方法，先定义一个半径为R 的圆形模板，模板内的总像素点个数为M，遍历每个寻找的轮廓点，对每个轮廓点取该圆形模板，统计模板内里在烟叶轮廓内部的像素点个数设为N。设定阈值C，当时，即认为该点为凹点。再用凹点个数除以整个轮廓点个数得到凹点比K，该值在一定程度上反映了重叠的可能性。

同时可以注意到，就算烟叶是重叠的，但叶柄在很大概率上仍然是分开的，通过叶柄的个数也可以在一定程度上作为判断的依据。

对原图进行阈值化后再使用形态开运算，能够消除叶柄部分，再用原图减去开运算后的图得到剩余叶柄部分，让面积≥1000 的值作为一个连通区域，计算连通区域数量，即可得到叶柄的数量。

以面积、周长、凹点比和叶柄数为特征，选取了一批重叠和单片的烟叶进行分类能得到测试集准确率接近90%的结果，较好地完成了重叠烟叶分级的第一步。

3.2 基于颜色差异的分割

当重叠的两片烟叶之间的颜色差距较大时，整个图片的颜色直方图会有两个较为明显的波峰，能够很容易想到通过一个阈值来将图片划分为两个类别，颜色值高于阈值的为类别1，低于阈值的为类别2，这样即可将重叠的烟叶分割成两片单独的烟叶。

为了使算法更具有普遍性和通用性，我们使用OTSU（最大类间方差）算法来寻找阈值TH。OTSU是一种常用的求分割阈值的算法，用来求出在目标与背景之间差别最大时候的阈值［13］，假设图像灰度值为0～255 之间，则用阈值k 将图像分为0～k 与k～255 两个类别C1和C2，用P1(k)和P2(k)分别表示被分到两类的概率，则有：被分到C1和C2的像素的灰度值均值为

其中m1(k)表示分到C1类的灰度均值，m2(k)表示分到C2类的灰度均值。

用mG表示整个图像的灰度均值，有：

相应地类间方差σ2B［14］为

在使用OTSU 求得阈值后，使用阈值化将低于阈值的像素部分置为黑色背景，用原图与阈值化后的图进行与运算就可得到高于阈值部分的烟叶图片，再做差即可得到另外一个烟叶部分，对上述图片的处理结果如下。

通过结果能够发现，对于颜色差距较大的图片，其分割结果较为理想。为了判断能否运用颜色进行分割，使用OTSU 算法中的最大类间方差作为衡量标准，训练一批图片得到一个阈值K 用于判断，对于最大类间方差＞K 的使用颜色分割方法，否则使用后面介绍的椭圆轮廓分割方法。

3.3 基于椭圆轮廓的分割

基于颜色差距的分割方法虽然简单方便，但适用性有限，因为并不是每个重叠烟叶都能用该方法获得较好的结果。为此进一步提出一种更具有普遍性的椭圆轮廓方法来适应更一般的情形。方法的主要思想是寻找重叠烟叶图片中的凹点，将图片中两个凹点之间的轮廓作为同一段轮廓，最后以找到的轮廓段进行组合拟合椭圆，找到最佳椭圆分割得到上层烟叶，再通过相减的方法得到下层烟叶。

首先使用3.1节中介绍的圆形模板面积法找到重叠烟叶图中的凹点，使用k-means 算法将凹点分为四类（如图8），同时用一个数组保存每个轮廓点的标签，先将刚各凹点标上不同的标签如-1、-2、-3、-4。将其余的各点都用0标记。

从任一点开始遍历，每遇到标签为0 的点就将其标签改为上一个凹点标签，即将两个凹点之间的所有点都归为了同一个轮廓点，用颜色将轮廓段标记出来如下。

可以使用4 个轮廓段的任意组合来进行椭圆的拟合，计算椭圆的面积Ea和烟叶轮廓面积C a，若0.4Ca＜Ea＜2Ca且椭圆在整个烟叶图像内，则将该椭圆纳入候选椭圆中。可以看到图10（b）、（c）都是拟合较好的结果，理论上都可能是上层的烟叶，故除了拟合的椭圆还需进一步进行筛选。

图1 数据集图片

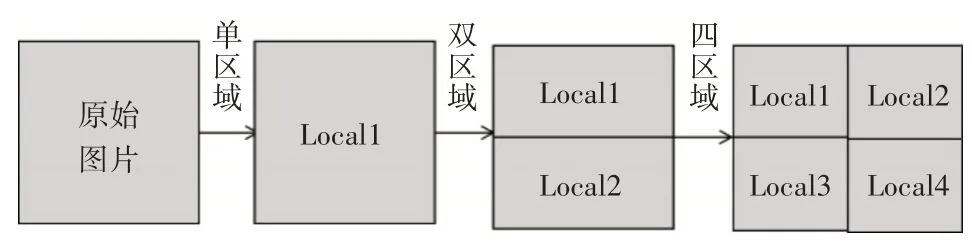
图2 LBP区域划分图

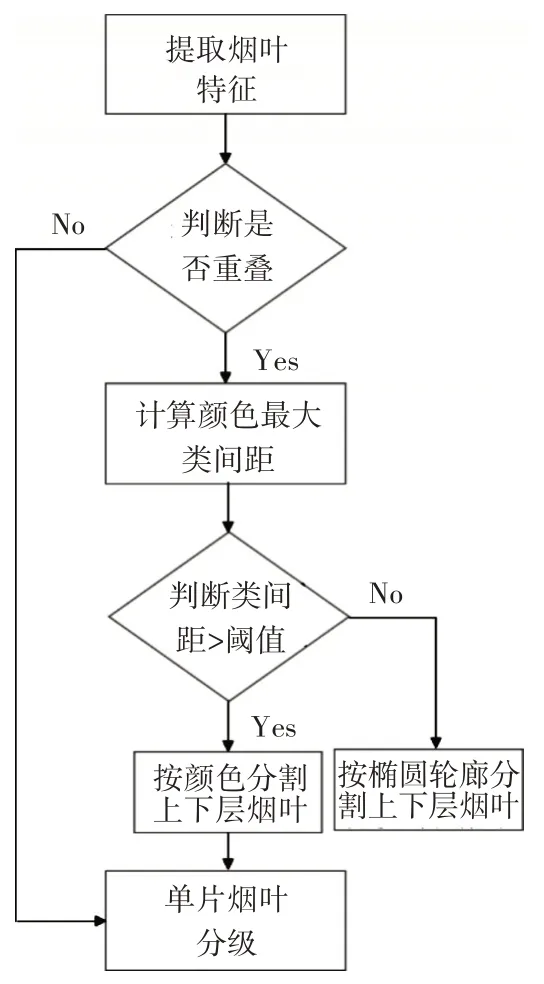
图3 烟叶分级流程图

图4 重叠烟叶图

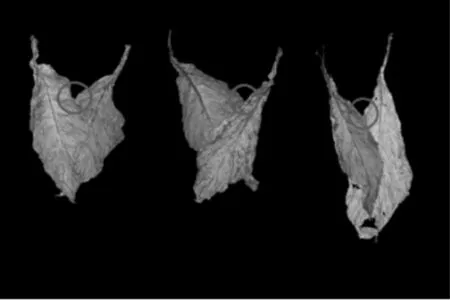
图5 凹点示意图

图6 叶柄剩余图

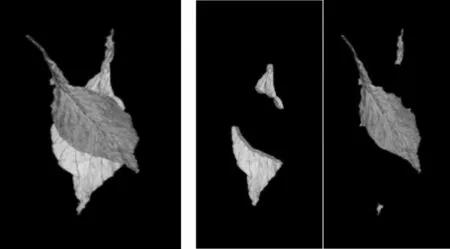
图7 分割前后图

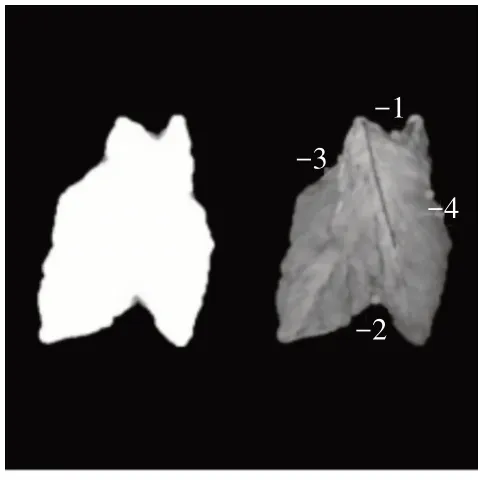
图8 凹点选取

图9 轮廓示意

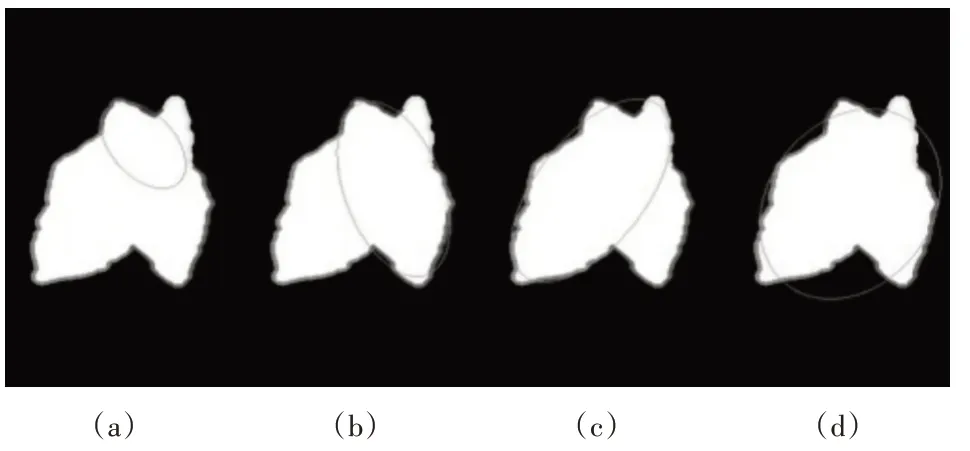
图10 椭圆拟合图

图11 椭圆拟合分割结果

图12 烟叶图及对应标签

图13 分割结果图

对于处于上层的烟叶，能够观察到其较为完整的主梗，而主梗近似为一条直线。故在这里使用Hough 直线检测来进行主梗的检测，首先对原图进行Canny 边缘检测，消除大部分的额外信息，此时只留下了轮廓和一些梯度强度较大的点，而主梗因为颜色较深，往往会保留下来，再以边缘点为圆心，将一定领域圆内的点都过滤，剩下的点中大部分为主梗边缘点。

此时再进行Hough 直线检测得到最佳拟合直线L，求得该直线段与水平方向的夹角Lα，图像的高度为H，计算椭圆中心到直线的距离D，同时定义椭圆紧密度Eρ为拟合出的椭圆内部白色像素占椭圆总像素的比例。计算所有候选椭圆与水平方向的夹角Eβ，椭圆的紧密度Eρ，用如下公式去计算所有候选圆的指标数：

对所有候选圆的Score 数进行排序，选取得分最高的椭圆作为最上层烟叶的拟合椭圆。以该椭圆的掩模可以分割出最上层的烟叶，然后再和原图相减，并通过面积滤波，就可得到最下层的烟叶图像。

3.4 单片烟叶实验结果

本次实验选取了B2F、B3F、C2F、C3F、C4F共五个等级的烟叶图片进行测试，其中共有4 批数据集，各数据集大小如下。

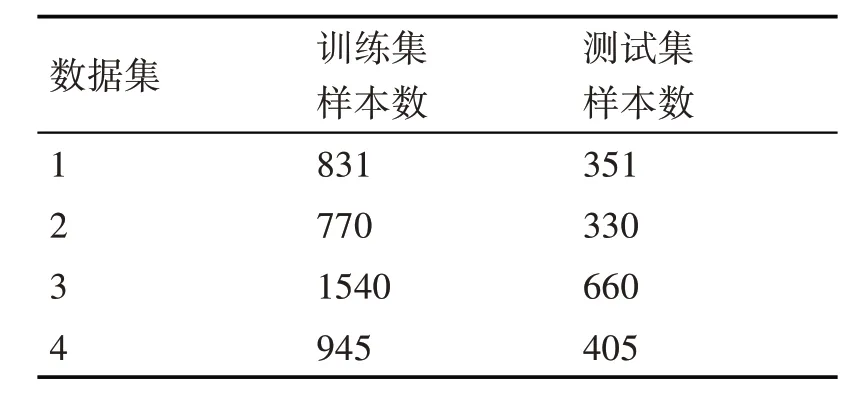
表1 单片烟叶数据集样本划分

在2.2 节中对于纹理特征的提取中我们做了3组不同的划分区域方式，使用数据集1 对3 种不同划分方式的结果进行测试，结果如表2。

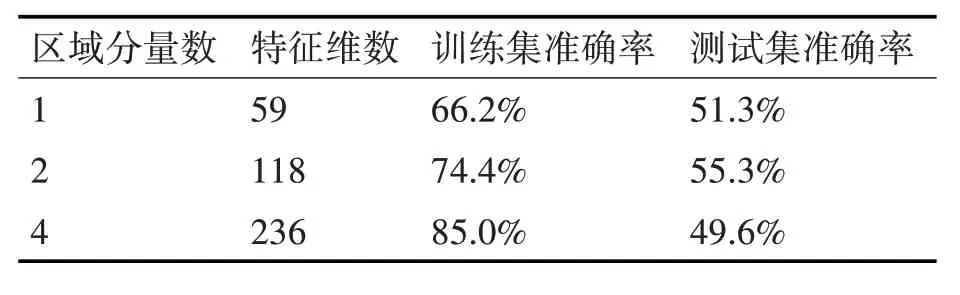
表2 不同区域划分方式结果

其中区域为2 时在测试集的准确率最高，故在后续实验中均使用2区域LBP划分方式。

然后对不同特征组合，固定使用逻辑回归作为分类器，并在数据集1进行测试，结果如表3。可以看出在一开始的纹理特征基础上添加颜色特征和形状特征后，准确率有了不少提高。

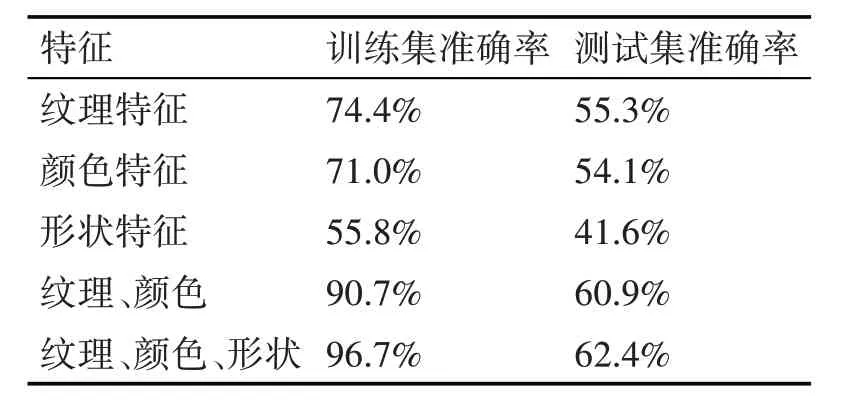
表3 不同特征组合测试结果

然后分别使用逻辑回归、SVM 以及Voting的集成学习方法对数据集进行分类，其结果如表4，从表中能够看出使用了Voting 方法后准确率在四个数据集均有了提升。

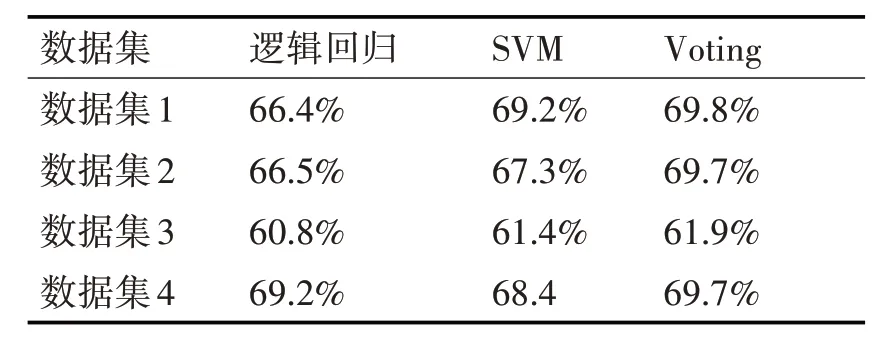
表4 各数据集分级测试集准确率

相应地为了进行分级结果的对比，我们还提取了一些深度特征进行实验，包括vgg16 最后池化层的输出结果、细粒度特征、自动编码器特征以及自监督学习框架SimCLR 提取的特征，在这里呈现出第一批数据集在上述特征下的结果，从表5 中看出上述特征的准确率均不如提出的方法准确率高，在其余三批数据集上的也表现出同样的结果。

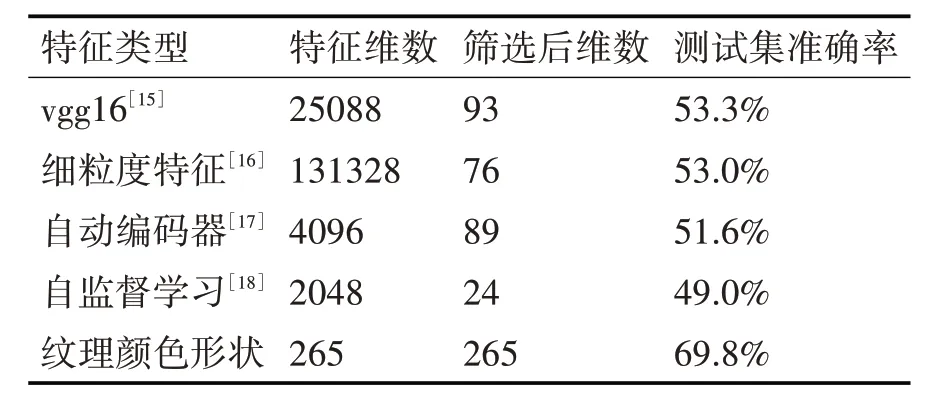
表5 深度网络模型和使用不同深度特征的分级结果

同时还选用了一些文献中的分级方法进行比较，这里我们选取了基于二进制粒子群（BPSO）和SVM 的分级方法、基于改进的聚类算法（ICA），遗传算法（GA），随机森林（RF）的分级方法以及基于PCA-GA-SVM 的分级方法，结果如表6。同样能看出来，上述方法准确率均没有特征提取方法高。

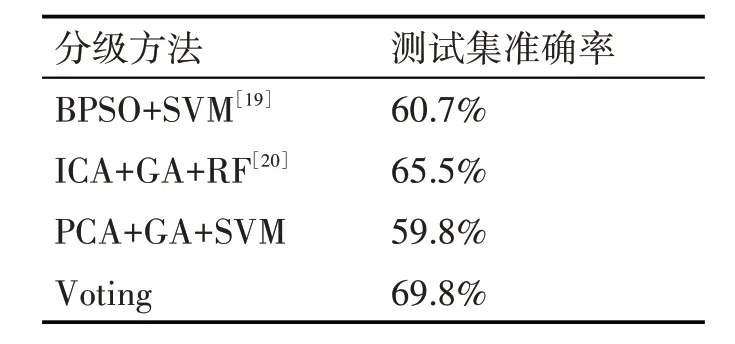
表6 不同分级方法结果

表7 椭圆轮廓分割后分级结果

3.5 重叠烟叶实验结果

选取3.4 节中的数据集1 中训练集的831 张图作为训练集。测试集有重叠烟叶图片200 张，用椭圆轮廓分割算法得到359 张分割后的烟叶图像，剔除不是重叠的烟叶41张和98张面积极其小的分割后的烟叶图像，最终用于分割实验的数据集有220张。

相应地，我们将基于椭圆轮廓分割后的图片同样用颜色标记上相应的标签。由于在合成时候已经获得真实标签，便可比较分割前后同样位置的点标签是否相同，以此定义分割结果指标

通过上面的椭圆轮廓分割方法分别获得上层和下层烟叶后，再用第2 节中的特征提取结合机器学习方法分别对上层和下层烟叶分级，得到最终的结果如下，在第一批数据集训练出的模型下，重叠烟叶的分级准确率达到了36.4%。

4 结语

本文使用了纹理、颜色和形状特征对单片烟叶进行分级处理，在四个样本数据集的准确率有67.5%。同时提出了一种针对特殊情况的基于颜色的重叠烟叶分割方式以及一种普遍适用的椭圆轮廓重叠烟叶分割方式，并对其分割后的结果进行分级测试，最终的结果为36.4%。从实验中看，深度学习目前并没有比传统方法好，下一步我们将分析原因，展开基于深度学习的烟叶分级研究。