基于SPSS 软件对高校成绩线性回归分析与预测*

张 梁 闫永红 赵 荣 张城瑞 文 丽 段珮华 于晋伟

（太原学院 太原 030032）

1 引言

高校教学质量是培养高素质人才的关键保证，因此对专业基础课成绩的科学分析对提高教师教学水平和更有效指导学生具有重要意义［1］。西方经济学和统计学是市场营销专业培养方案中的专业基础课程，从工商管理类角度而言，可以拓展学生思维宽度和角度，使其掌握从多角度，多维度，多层面分析市场营销专业基本理论，同时，经济数学是结合数学理论研究的经济学，具有扎实的数学理论基础又具有经济理论基础，该课程不仅为市场营销专业后续课程提供必备的数学工具，而且是培养工商管理类高校学生数学素养和理性思维能力的最重要途径。鉴于此，对经济数学、西方经济学、统计学卷面成绩的相关性研究显得尤为重要。

SPSS 软件是一组专业的、通用的统计软件包，同时它也是一个组合式软件包，兼有数据管理、统计分析、统计绘图和统计报表功能。突出的特点就是操作界面极为友好，它将几乎所有的功能都以统一、规范的界面展现出来，在学科统计方面已经有了较为成熟的应用［2］。文献［3］利用统计分析软件SPSS 对高校学生线性代数成绩进行差异性检验，得出课程成绩差异性情况和男女同学成绩差异情况和相关性检验，此外通过相关性检验得出线性代数与其他课程相关情况。文献［4］利用统计分析软件SPSS 验证高校多媒体辅助语言学习软件对学生提高英语四级的帮助，结论表明听力、阅读、写作、翻译和总成绩皆与学习软件评分成正相关性，据此给出提高听力、阅读的建议。文献［5］利用统计分析软件SPSS 具体分析了学生数学、语文成绩之间的相关性，并介绍了SPSS 软件在教学中的广泛应用。

但此类研究未见依据已修专业基础课程成绩，进行相关性分析，深入研究学生成绩及其影响因素，优化未修专业课程安排和教师对该专业后续课程成绩进行预测。故笔者依据太原学院管理系2020 级市场营销专业75 名学生的经济数学、西方经济学、统计学已修卷面成绩进行相关性研究，继而针对学生知识水平、班级学习风气进行精准评估和提高教师授课效果。

2 研究对象

所选取的研究对象为太原学院管理系2020 级市场营销专业75 名学生经济数学、西方经济学、统计学已修课程成绩，此成绩来源为太原学院教务处。试卷由教研室教师共同命题，由教务处审核，三门专业基础课试卷分为A、B 卷，均采取闭卷考试，考试完毕由教研室教师流水阅卷，保证了数据样本的真实性，汇总得到学生三门专业基础课卷面成绩。

3 卷面成绩分析

3.1 成绩基础情况描述性统计

选取数据的真实性和可靠性是进行综合评价的重要保障，需要真实客观的学生成绩作为支持，同时所选取的学生考试成绩来源具有权威性，可以保证高质量反映分析对象的特征［6］。运用SPSS 软件进行学生已修课程的卷面成绩进行分析，如表1所示。

由表1 卷面成绩统计量可得出，经济数学、西方经济学、统计学学生已修课成绩平均分分别为66分、68.5分、72.8分，三门科目卷面及格分数均为60 分，由此来看，统计对象全班三门专业基础课成绩属于中下水平；三门专业基础课程成绩最低分为42 分、39 分、39 分，最高分分别为85 分、87 分、93分，三门课最高分均在85分以上（包含85分），课程成绩属于上等水平，虽然没有出现满分和一位数成绩，即描述性统计量中未出现极大值和极小值，但综合分析三门课极小值均未达到及格标准（60分），且三门课最低分均在40 分左右，与最高分比较，说明成绩跨度大，具有深层次分析的必要性；其次结合其他描述性统计量可以看出，此次样本选取对象合理，数据具有真实性，适合对三门专业基础课进行深度的科学分析。

将三门专业基础课成绩运用统计分析软件SPSS进行数据正态性检验，如表2和图1。

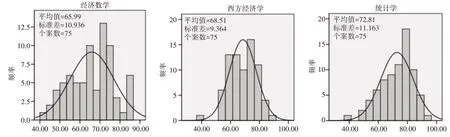
图1 分布直方图

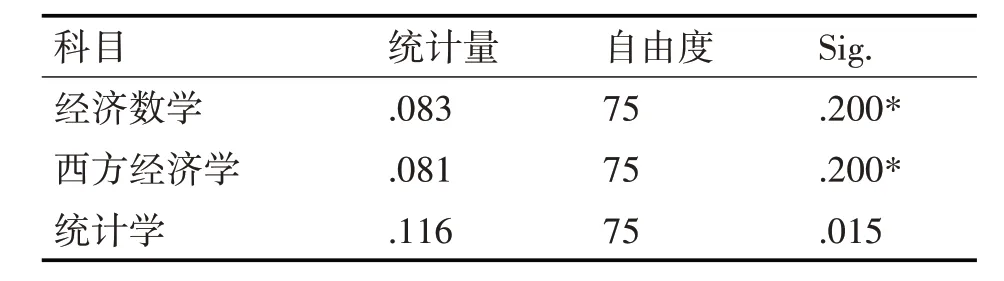
表2 课程成绩正态性K-Sa检验

如图1 课程成绩统计直方图所示，横坐标为成绩分数段，纵坐标为成绩出现的频数，直方图整体表示连续性成绩的频数分布，由图1 可以看出根据直方图汇出的曲线相似正态分布曲线［7］，清晰明了反映出三个科目正态分布情况，进一步分析，由表2 所示，三个科目正态性K-Sa 检验sig。值均大于0.05 证明所研究课程成绩服从正态分布，且P 值越大，越服从于正态分布［8～9］。

综上所述，对三门基础专业课进行描述性统计分析所得结果表明整体成绩集中于60分至80分区间，属于中等偏下水平，一定程度上说明了经济数学、西方经济学、统计学课程需要总结教学经验，提高教学质量，与此同时和班级学风建设，学生学习态度也有密切关系。

3.2 卷面成绩相关性分析

对三门专业基础课的研究过程中，研究对象之间存在相互关联现象，卷面成绩间均为连续数值型变量，并且成绩归属为75 名学生三门科目成绩，即成绩来源为同一群体，鉴于此采用Pearson 相关性分析进一步研究。Pearson 相关系数，又称积差相关系数，是表达数值型变量间线性相关程度及方向的统计指标，故而对其三门科目进行相关性分析具有较大的实用价值［10］。

式中，n 代表数据样本数量，xi和yi分别代表双变量数值。

应用SPSS 软件将经济数学、西方经济学、统计学三门科目进行双变量相关性分析，其运行结果如表3所示。

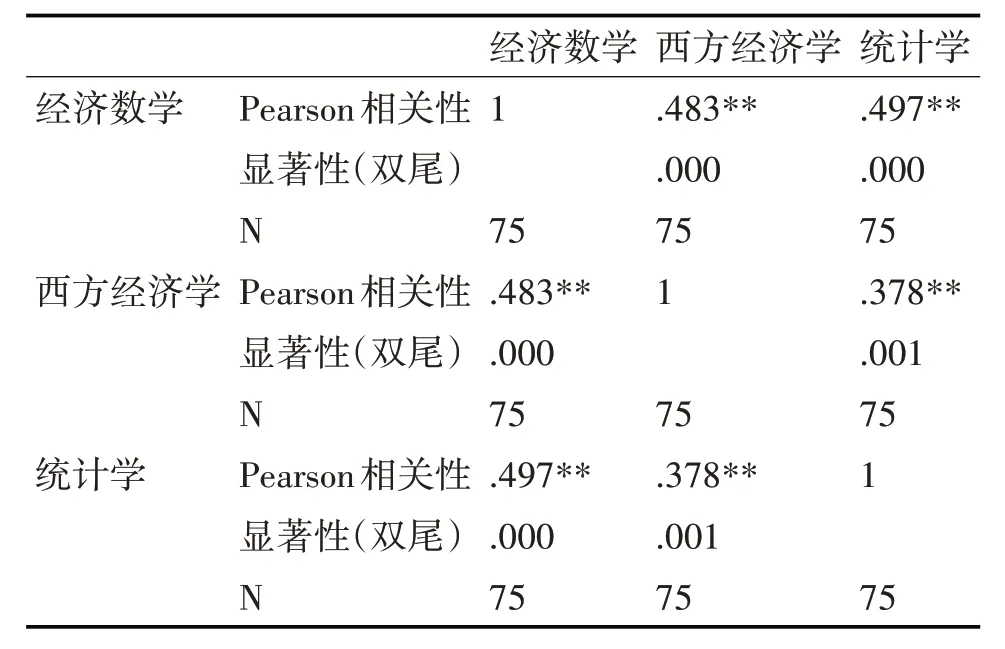
表3 三科目成绩双变量相关性分析表

查阅相关文献，P<0.01 时表明两个变量相关性显著，P 值为0 拒绝原假设（没有相关性），Pearson相关性系数大于0，表明双变量呈线性正相关关系［11～13］。表3中经济数学与西方经济学和统计学关系数分别为0.483 和0.497，P 值为0.000。据此，依据文献和表3 可以判断经济数学与西方经济学和统计学之间正相关性极显著。西方经济学和统计学之间虽然也呈现正相关性，但相关系数仅为0.378，且P值为0.001，表明西方经济学和统计学未达到高度显著性相关。

综上述分析可得，经济数学与西方经济学、统计学在知识体系、学习内容上有很大相同之处，经济数学可视为西方经济学和统计学的基础，经济数学中培养的逻辑思维能力对学好西方经济学和统计学具有重要作用。与此同时，教师在教学过程中应该重点使学生掌握经济数学中侧重于西方经济学和统计学的章节，为学生后续课程奠定扎实的基础。

3.3 卷面成绩多元线性回归预测

多元线性回归指两个及以上影响因素作为自变量来解释因变量的变化，可以在完成三门专业基础课相关性检验的前提下，对因变量进行预测估计［14］。三个科目经过双变量相关性分析后，经济数学，西方经济学，统计学三者之间正相关性极显著，此外学生所学课程顺序（学期）为经济数学，西方经济学，统计学。鉴于此，将经济数学，西方经济学课程成绩视为自变量X1，X2，理论统计学课程成绩视为因变量Y，自变量经济数学和西方经济学与因变量统计学满足线性相关，多元线性回归模型为

Y=b0+b1·X1+b2·X2（2）

其中，b0为常数项，b1为X1、X2固定时，X1每增加一个单位对Y的偏回归系数。

运用SPSS 软件建立对统计学课程成绩预测的多元线性回归模型，多元线性回归模型摘要运行结果如表4。

表4 多元线性回归模型摘要

分析表4，此多元线性回归模型摘要中相关系数R 为0.552，表明2 个自变量X1，X2能够解释因变量Y变化原因的52.2%，即理论统计学课程成绩中有52.2%是由经济数学和西方经济学所影响的。R2称为方程决定系数［15］，代表回归模型中自变量对因变量变异的解释程度，但R2是基于样本数据计算出来的，会夸大自变量对因变量变异的解释程度，调整后的R2剔除了自变量个数的影响，校正了R2对总体自变量对因变量变异解释程度的夸大作用，准确性更好，此方程调整后R2为0.252，大于0.25，表明拟合度较好。

依 据 表5，b0为30.462，b1为0.418，b2为0.215，所以多元线性回归方程为

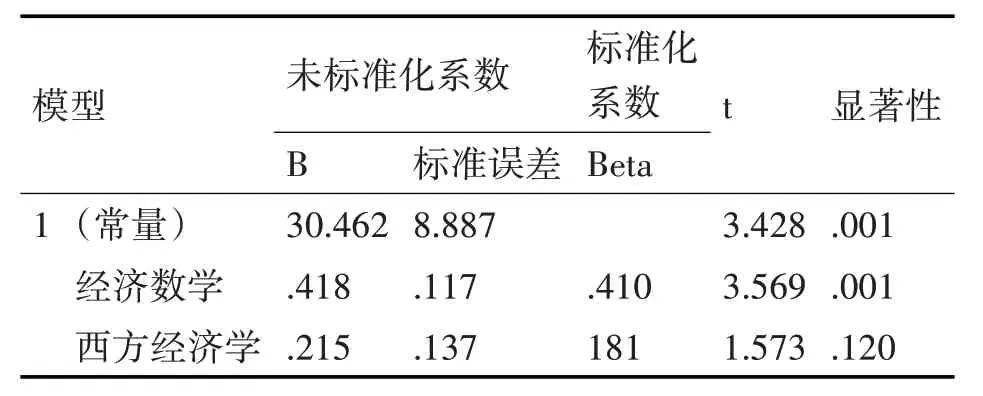
表5 回归系数与显著性表

Y=30.462+0.418·X1+0.215·X2（3）

方程式（3）表示在已知经济数学和西方经济学卷面成绩的前提下，可以理论预估统计学课程卷面理论成绩，以期能够帮助教师在教学过程中抓重点、夯基础、使任课教师在前期对学生基础知识有所了解掌握，进而提高统计学教学效率，更好帮助学生在统计学课业取得更大进步［16～17］。

4 结语

本文以太原学院管理系2020 级市场营销专业75 名学生经济数学、西方经济学、统计学卷面成绩进行正态分布检验及相关性分析，并且建立了卷面成绩多元线性回归模型，得出了经济数学、西方经济学、统计学线性回归方程预测方程。研究结果表明：

首先，将经济数学、西方经济学、统计学成绩进行基础情况描述性统计，分析结果说明所选取对象合理，数据真实；其次运用统计分析软件SPSS 进行数据K-S 检验，运行结果显示三个科目正态性K-Sa 检验sig.值均大于0.05，证明所研究课程成绩服从正态分布，但整体成绩属于中等偏下，需要进一步提高教学质量和学风建设，进一步对三科目成绩进行双变量相关性分析，依据结果判断经济数学与西方经济学和统计学之间正相关性极显著；最后将经济数学，西方经济学课程成绩视为自变量，理论统计学课程成绩视为因变量，得到理论统计学课程成绩多元线性回归方程Y=30.462+0.418·X1+0.215·X2，多元线性回归方程中相关系数R 为0.552，拟合度较好。

据上述研究结果，给出以下建议：

1）针对研究结果经济数学、西方经济学、统计学课程成绩整体属于中下水平，学生应对所学内容进行预习、复习，提高学习效率，转变学习态度，在思想上提高认识，切勿针对考试进行突击性学习攻关，与此同时教师在日常教学过程中提高上课效率，课后对学生学业进行督导，定期对学生学业疑问进行解答帮助。

2）针对研究结果经济数学、西方经济学、统计学课程正相关性极显著，不同科目任课教师应定期进行一定沟通，相互交换学生学习难点、重点，对学业有困难学生任课教师协同发力，帮助其提高学习信心。学生应整体把握三门专业课知识点，对经济数学基础知识进行回顾性复习，对西方经济学、统计学进行针对性预习，全面性复习。

3）教师可依据多元线性回归方程，依据学生经济数学，西方经济学卷面成绩对统计学成绩进行预测，有目的性的调整教学安排，学生可依据自身成绩对即将开始的统计学科目进行预测，争取取得更大的收获。