期望空间分辨率的激光雷达扫描算法*

李树青 林靖宇

（广西大学电气工程学院 南宁 530004）

1 引言

近年来，尽管三维激光雷达已经商用，但二维激光雷达由于价格低廉而非常受欢迎并得到了大量的应用［1～3］。在未知复杂环境中进行扫描和三维场景重建［4］时，常常会因为场景中物体尺寸及距离等问题，使得固定角分辨率的普通激光雷达有着无法调和的矛盾。如果选择分辨率较低的激光雷达，由于远距离造成的采样稀疏，必将导致远距离小物体的漏扫描，而且在点云配准时由于重合度不高造成配准精确度的下降［5］。而当选择分辨率较高的激光雷达时，首先，高昂的价格使得其应用范围较窄［6］。其次，近距离物体表面上的扫描点将变得异常稠密，造成了大量的数据冗余，需要进行点云压缩［7～8］。

普通激光雷达的扫描方式都是固定角分辨率，所以普通激光雷达都存在采样不均的问题，因此在远处的物体，其表面相邻采样点的间距会变得稀疏。例如，图1 中，由于距离激光雷达的远近不同，左侧物体被激光雷达扫描的相邻采样点的空间分辨率η1相较右侧物体的空间分辨率η2要小。

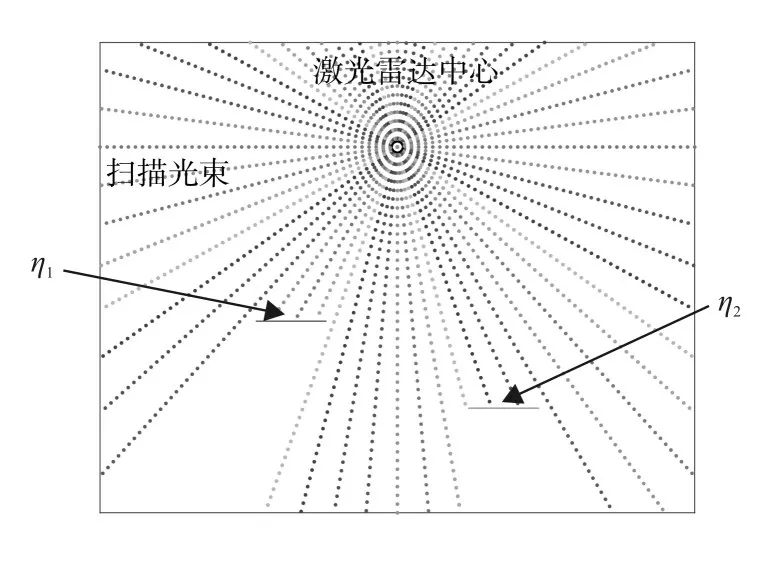
图1 激光雷达扫描示意图

2 系统设计和扫描算法

为了解决采样不均问题，首先对现有系统方案进行回顾，再设计适合自身需要的系统，并进行系统分析和算法设计。

2.1 系统设计

为了提高精度和效率，很多研究者使用二维激光雷达和伺服系统来搭建三维激光雷达系统，在大部分方案中，他们的伺服系统都是旋转平台的转轴处于二维激光雷达的扫描平面中［9～11］，其他方案包括设计一个云台使其有规律的摆动［12］，使用弹簧让其自由的振动［13］，使旋转轴和扫描平面倾斜某个角度［14～15］，但这些方案都没有致力于解决采样不均的问题。基于上述方案的启发，为了达到水平角分辨率可控的目标，提出的系统方案如图2 所示，此三维激光雷达原型系统主要部件为一个二维激光雷达，一个单轴云台和一个长臂支架。长臂支架被安装在云台上使得它可以在水平方向上旋转，而二维激光雷达被安装在长臂支架的另一端并使得它可以进行竖直方向的扫描，这样既把旋转轴从扫描平面中分离了出来，又使得扫描数据的转换变得容易，如式（1）：

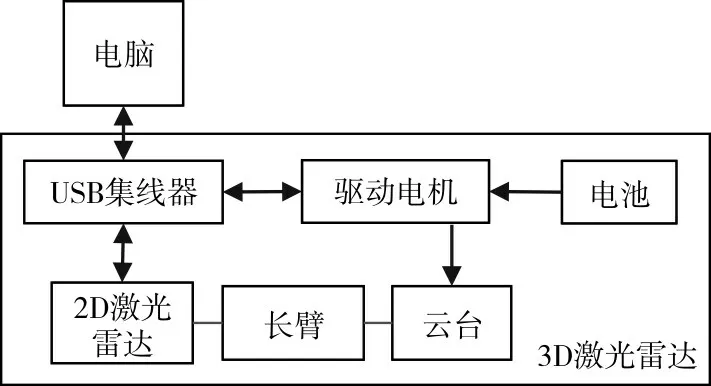
图2 三维激光雷达机电框图（箭头表示电气连接，连线表示机械安装）

这里{x，y，z} 为三维点云坐标，{d，θ} 为二维激光雷达扫描数据，ϕ为云台旋转角，R为长臂长度，Δθ为误差角。

2.2 系统分析

激光雷达系统被用来获取周围环境的结构信息，为了获取足够的细节信息，激光雷达需要采集更加大量的数据，这将导致高额的硬件成本和数据处理成本。

对于激光雷达，在同一水平角度ϕ时，扫描数据处于同一垂直平面，而在同一垂直角度θ时，扫描数据却通常不是处于同一个水平平面。故假定激光雷达以固定的角步进进行水平扫描，有水平角速度ωs与水平角步进Δϕs的关系如下：

其中T0激光雷达的采样间隔时间。

想要控制所有待扫描物体表面的采样密度，需解决如下三个问题：首先是表面检测问题，在空白的区域进行高分辨率扫描将导致数据处理问题，而设置一个密度阈值将导致稀疏的表面采样点被舍弃。其次是如何根据采样密度来确定激光雷达的角步进。最后是如何在一个扫描周期内对物体表面进行再扫描。

对于前两个问题，首先推导密度和激光雷达角步进的关系。因为激光雷达采集到的数据为物体表面的采集点数据，所以密度就是单位平方空间内采样点的数量。故而，它们的关系如下：

其中ρm为物体表面的密度，εm水平空间分辨率，ξm为垂直空间分辨率。

假设物体都是竖直放置的，即物体表面垂直于激光雷达，有εm=dmΔϕs和ξm=dmΔθs，这里Δθs为垂直角步进，而dm为激光雷达到物体表面的距离。在水平面中，当物体表面与激光束的夹角不是直角时（设为β），有：

在此激光雷达原型系统中，由于垂直角步进是固定的，故只能通过调整水平角步进Δϕs来改变水平空间分辨率εm。

对于第一个问题，可以通过角度β的值来检测物体。在一组采样数据中，角步进Δϕs和Δθs，距离dm都是已知的数据，因此角度β就可以通过计算得到。在一个空白的区域，角度β几乎为零，而当角度β较小时，意味着物体平面是非常倾斜的，这几乎无法被激光雷达扫描到。所以，忽略角度β较小的区域不会造成远距离物体表面的漏扫描。

对于第二个问题，在获得密度ρm、距离dm和角度β后，很容易计算角步进Δϕs。

对于第三个问题，由于三维激光雷达原型系统的特殊设计，在不被遮挡的情况下，一个扫描周期内同一物体会被扫描两次（分别定义为正扫描和逆扫描）。所以根据在正扫描位置ϕp获得的空间分辨率εm，可以用来调整逆扫描位置ϕq的角步进Δϕs。它们的几何关系见图3，ϕq能通过如下公式计算：

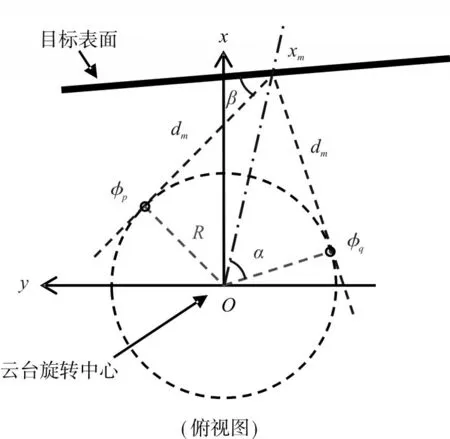
图3 扫描几何原理图

2.3 自适应扫描算法

首先确定期望的空间分辨率εs和扫描距离ds，之后初始化角步进Δϕs0并用于一个扫描周期中的正扫描：

之后在位置ϕp估计扫描点的密度ρ，这里有两种方法进行密度估计，一个是直方图统计，另一个 是核密 度 估计［16～17］。假设有 一 组N 个数据 点{(xn，yn，zn)}，选取二维高斯核进行核密度估计，有

其中，h 为高斯核宽度。选取范围ϕp±Δϕp内的数据进行核密度估计。

在得到扫描平面内所有点的密度估计值ρ之后，可以找到对应的物体表面点的位置xm。而局部最大的密度估计值所在的位置就是物体表面点的位置。

使用xm位置的密度ρm=ρ( )xm，可以通过式（2）求出εm，通过式（3）求出β，通过式（4）求出ϕq，这样，就可以在ϕq处更新扫描角进度Δϕs(ϕq)，使得物体表面的空间分辨率达到期望的εs，当完成正扫描后，在同一扫描周期内使用新的角进度进行逆扫描。

3 实验

在本文的三维激光雷达原型系统中，使用的二维激光雷达型号为Hokuyo URG04LX-UG01，它的角分辨率为0.36°；云台由角分辨率为0.02°的旋转平台和分度高达128 的驱动电机组成，而且ϕ角能直接通过电机驱动程序读取。

为了验证扫描算法的效果，实验场景为激光雷达扫描周围零散的盒子，盒子的大小和距离各不相同，进行多次实验，其中一次的实验布置图如图4所示。通过扫描盒子的表面，对不同距离和方向的盒子表面的采样空间分辨率进行比较。首先以固定的水平角步进Δϕs=0.1°进行扫描（对应的期望距离为1m，期望空间分辨率为2mm），之后使用自适应扫描算法进行扫描（期望空间分辨率为2mm），实验结果如图5所示。

图4 实验布置图

图5 实验结果（点划线为固定分辨率扫描，实线为自适应分辨率扫描，横虚线为期望空间分辨率）

首先，#1～#4 盒子都被正确的检验出来，说明物体检测算法正确的反映了盒子位置。之后，对比固定角步进扫描和自适应扫描得到的数据中物体表面的空间分辨率εm，在图5 的正扫描图中，固定角步进扫描和自适应扫描得到的空间分辨率几乎是一致的，因为它们都使用了同样的角步进。当自适应扫描开始更新角步进后，如图5 的逆扫描图所示，四个盒子的扫描空间分辨率（实线）都降到了期望空间分辨率（虚横线）左右。而固定分辨率扫描的空间分辨率（点划线）仍随距离的变化而变化。

进而，通过实验研究了固定分辨率扫描和自适应分辨率扫描在不同距离和不同角度时对物体轮廓的测量精度的影响。实验条件如下：两个不同尺寸的物体（宽度为0.048m 的椅子脚和宽度为0.15m的抽屉），三种不同的距离（500mm，1000mm 和2000mm）和两种不同的倾斜角度（0°和60°）。对比结果如图6 所示，固定分辨率扫描方式随着距离物体的距离不断变大，扫描精度不断的变差（相对误差从1%增加到15%），而自适应分辨率扫描即便距离增大到2000mm，扫描的相对误差也没有超过2.4%。所以自适应分辨率扫描能有效地克服激光雷达扫描精度随距离增大而变差的缺点，这表明了本算法在测量精度方面的优势。

图6 扫描精度实验结果（虚线为固定分辨率扫描，实线为自适应分辨率扫描）

最后，我们对随意放置在激光雷达周围的物体分别用固定分辨率和自适应分辨率扫描进行尺寸测量，并对比测量精度，三次实验的结果如表1 所示。可知，在绝大多数的测量结果中，自适应分辨率扫描的结果都更加精确（粗体为更好的测量结果）。当固定分辨率扫描已幸运的达到较高的扫描精度时，自适应扫描的精度提升较少，如实验1 的#2 和#3。而当较大的#1 目标处于较远距离时，自适应分辨率扫描都取得了很好的扫描精度（见实验2和实验3）。

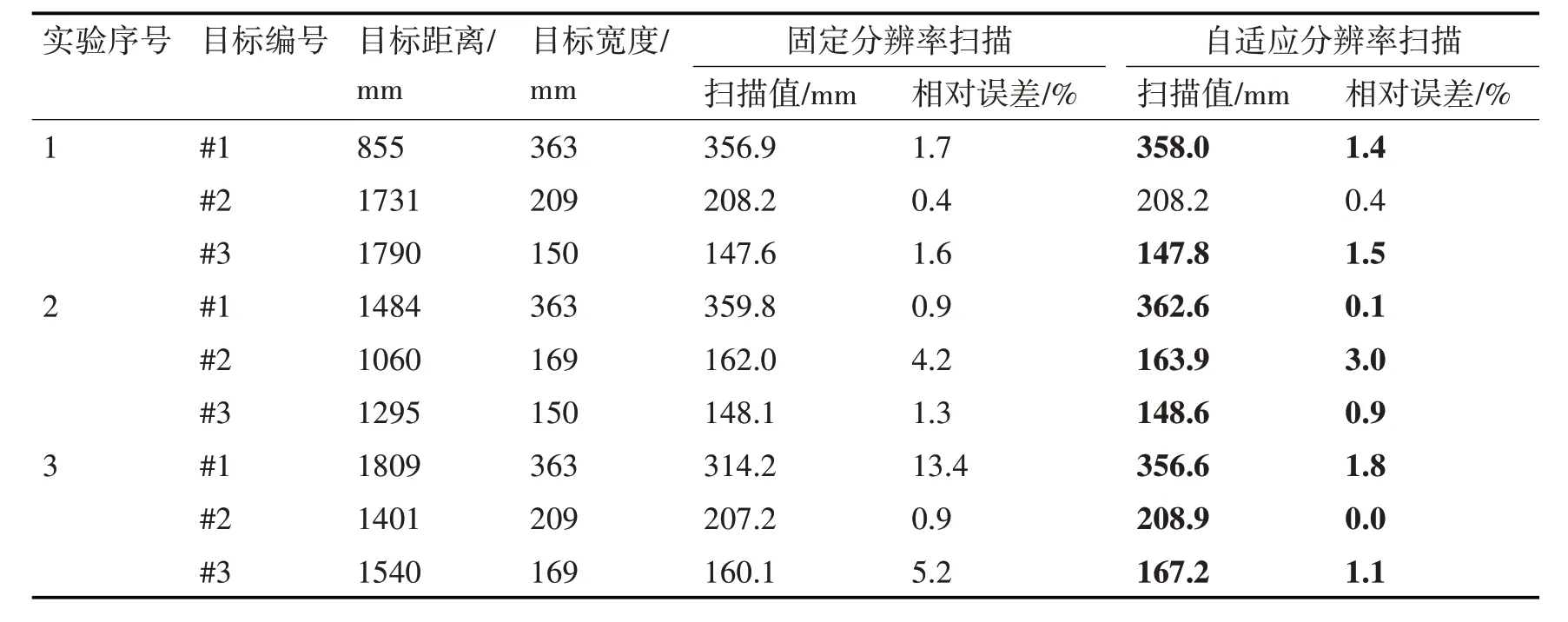
表1 尺寸测量对比表

4 结语

为了解决采样不均带来的远距离小物体漏扫描、近距离数据冗余和扫描测量精度降低等问题，提出了一种自适应分辨率扫描算法，根据物体距离激光雷达的距离和物体表面的角度来调节扫描步进以达到期望值空间分辨率。并通过设计一种新型的激光雷达系统来搭载实现此算法。对比实验表明，本算法能准确定位物体表面且能把扫描空间分辨率调节到期望值，扫描精度对比实验证明了其相比固定分辨率扫描方式能得到更高扫描精度的数据。

由于本激光雷达系统扫描得到的点云数据不是从单一视角获得的，而是从一个宽泛的视角范围获得的。这样的点云数据有可能提高点云配准和三维物体识别的鲁棒性，这是下一步的研究内容。