基于大数据分析的污染物追踪预测算法*

潘欣玉 张孝苗

（中国石油大学（华东）计算机科学与技术学院 青岛 266580）

1 引言

现阶段对于区域环保监测点获取的污染物数据，其应用主要是计算空气污染指数［1］，分析区域环境质量，获取污染物排放量［2］等方面。人工智能与大数据发展迅速，基于大数据分析方法对环保监测点污染物数据［3］进行主要污染物的提取，能够追踪到污染物排放较多的企业行业对其进行有效监控，为环境管理部门提供可靠的技术支持，而且也为大气污染的预防奠定了基础。

现阶段针对获取的污染物数据进行关键污染物获取的方法主要是应用计算Person相关系数法［4］或污染分指数等数理知识进行，然而此类方法结论过于依靠数据量情况，准确性不能得到保证且计算过程复杂通用性不高。目前污染物追踪工作中，主要有无人机遥感监测大气污染源追踪定位［5］、PHP源代码SQL 注入漏洞检测方法［6］，HYSPLIT 提供的聚类分析工具作聚类分析对比［7］，存在着成本开销较大、精度较低、模式复杂适用性不高等问题。针对上述问题，结合PCA 算法［8］可在多维数据指标中进行主要成分提取的功能，以及关联规则算法［9］可挖掘数据参数间关系的优势。我们提出了一种基于大数据分析污染物追踪预测算法，可结合本文方法分析结果比对区域中各类型污染企行业排放物，实现主要污染物的追踪预测。

2 相关工作

目前对于主要污染物的提取工作及追踪工作主要有降维处理污染物数据及采用统计学方法计算空气污染指数、Person系数、平均影响值。SVD［10～11］是一种矩阵奇异值分解技术，Guiqian Liu 等［8］通过分解技术所得的低秩矩阵尽可能逼近原始矩阵，使得低维数据能够充分反映原始高维数据的主要信息，得到可反映全局污染物信息的主要污染物。叶斯琪等［12］采用统计学方法获得各个污染物的空气污染分指数值，降序排列实现对各污染物所占比重的排序从而进行主要污染物的提取。平均影响值（MIV）方法［13］通过计算各个污染物的平均影响值也可筛选出对污染物浓度影响较大的因素。文献［14］采用的Person相关系数法，通过对监测点所有监测指标数据的分析，借助于SPSS 软件确定每种污染物的相关度，据相关度结果发现主要污染物指标。

在主要污染物追踪方面，可运用统计方法和后向轨迹模拟对所获数据进行分析［7］，在获得地区污染物监测数据后，模拟大气气团后向轨迹以反映污染物在区域内的传输特征，利用美国空气资源实验室的HYSPLIT 模型［5］提供的聚类分析工具作聚类分析对比，分析大气污染的输送路径及特征。基于萤火虫算法［15～16］的大气污染源追踪定位方法［17］是由陈晨等人在2019 年提出的，原理是利用萤火虫算法对无人机遥感监测［18］下污染源进行追踪定位，将萤火虫种群分为无数个单独子群，根据各个子群之间信息交流找出污染源追踪查询最优方案，实现大气污染源追踪定位。古添发等［19］应用无线智能遥感监测大气污染源追踪定位系统对污染物进行追踪溯源，樊东红等［20］发明一种基于无线云传感网的大气污染物在线监测系统，设置有用户终端、无线云传感网［21］、系统分析及污染物监测模块等不同功能模块，用户终端通过访问数据总汇终端对大气污染状况及污染物源头信息进行了解控制。

3 基于大数据分析的污染物追踪预测算法

本文提出基于大数据分析的污染物追踪预测算法，首先对区域中主要大气污染物进行提取工作，在提取出区域主要污染物基础上对主要污染物进行追踪。本文基于区域环保监测点下真实数据，应用主成分分析方法（PCA 算法）进行主要污染物提取工作，PCA 算法降维后依据各维度贡献率大小，选取维度之和大于85%的污染物作为主要污染物，在提取出主要污染物的基础上应用关联规则算法进行关联性发现，定性提取出与主要污染物关系密切的污染物，定量发现排放量的关联性。最终结合分析结果比对区域中各类型污染行业排放物，进行污染物跟踪。

3.1 基于PCA算法的关键污染物获取

PCA 算法思想是通过构造由原变量线性组合形成的新变量，使新变量在互不相关的前提下尽可能多地反映原始变量的信息，每个新的特征有其独特的含义，将n 维特征映射到k 维上（k＜n），这k 维特征是全新的正交特征，被称为主成分。主成分是重新构造出来的k 维特征，而不是简单地从n 维特征中去除其余n-k 维特征。每个新的特征有其独特的含义，数据信息主要反映在方差上，方差较大的特征维度可以反映主要信息包含在原来的多个变量中，通常用累计方差贡献率来衡量。一般选取累计贡献率在75%～95%左右的维度作为PCA 降维的参考维度。本文对实际环保监测点的数据样本进行主成分分析，环保监测污染物指标总共6种，通过主成分分析方法确立所有特性指标的主成分，选定累计贡献率85%作为参考维度，通过主成分确立出影响该区域大气环境的主要污染物指标。

式（1）中cov(Zi，Zj)为指标Zi与Zj的协方差，解相关性系数矩阵的特征方程|R-λIm|=0，其中，λ=[λ1，λ2，…，λn] ，将求得的特征值排序，选取的出的主要污染物个数取决于累计方差贡献率，通常累计方差贡献率大于85%时对应的前p个主成分便包含m个原始变量所能提供的绝大部分信息。方差贡献率和累计方差贡献率分别如式（2）、（3）：

取前p 个特征值对应的特征向量构成降维后的坐标系Vp=[ ]V1，λV2，…，Vp，即主成分分析的解，据p 个主成分中特征值的大小，提取出主要污染物。

3.2 基于关联规则算法的污染物排放量关联性分析

污染物指标不仅具有相关性关系，在排放量方面也具有关联关系。为了挖掘这些指标排放量的关联关系，本文使用双重关联规则算法来分析。针对所获得的环保监测数据X，首先对六种环保指标依据排放量数值情况进行分段处理，将预处理后的数据集进行双重关联规则关系发现。

本文对环保指标排放量进行关联性分析，满足支持度阈值的参数形成1_项频繁关键词集，支持度公式如下：

sup(a→b)表示关键词集｛a，b｝的支持度；P(a∪b)表示关键词集｛a，b｝在数据集中出现的概率0≤P(a∪b)≤1；num(a∪b)表示关键词集｛a，b｝在数据集中出现的次数；num(dataset)表示数据集中数据记录的个数。所以设置支持度阈值时，相对置信度而言可以小一点，如果支持度阈值过大则结果准确度不高。置信度反映了参数之间的关联程度，设置置信度阈值时尽可能大一点。置信度公式如下：

其中，conf(a→b)表示关键词集的置信度；P(b|a)表示在数据集中关键词集｛a｝发生的情况下关键词集｛a，b｝也同时发生的条件概率0 ≤P(b|a)≤1。关联规则集是由所有k_项频繁关键词集得到的满足置信度阈值的所有关联规则组成的集合即为一个关联规则集。若第y 个关联规则为a[y]→b[y]，则关联规则集Rules={a[y]→b[y]}，其中y=（1，2，…r），r为满足条件的关联规则的个数。

4 实验与结果分析

4.1 实验数据

本实验使用实际环保监测数据，数据来源于同一区域不同监测点逐时刻监测结果，共计8 个环保监测点，实验指标有SO2，NO2，CO，O3，PM10，PM2.5六项，共有69340条数据。

4.2 数据预处理

在进行主要污染物提取之前，需对原始监测数据进行数据预处理，以提高后期数据分析的效率、准确度，减少后期算法工作的计算量。数据预处理包括数据清洗、数据标准化。数据清洗主要内容是去除无意义数据、检查数据一致性、处理重复数据；数据标准化主要原因是原始数据不同指标之间数值尺度差别较大，为较少对算法结果影响，采用StandardScaler方法进行标准差标准化，将每一维特征均处理为均值为0方差为1的正态分布。

4.3 关键污染物获取分析

应用主成分分析法（PCA）对环保监测数据进行主成分提取，结果如表1所示。

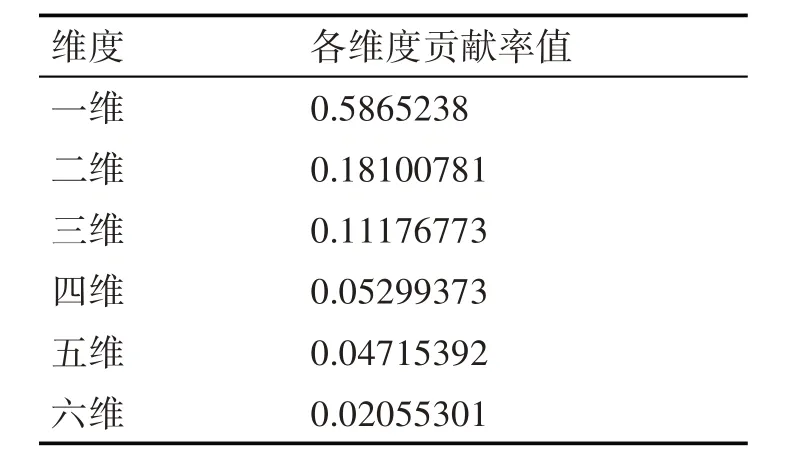
表1 主成分分析后各维度贡献率

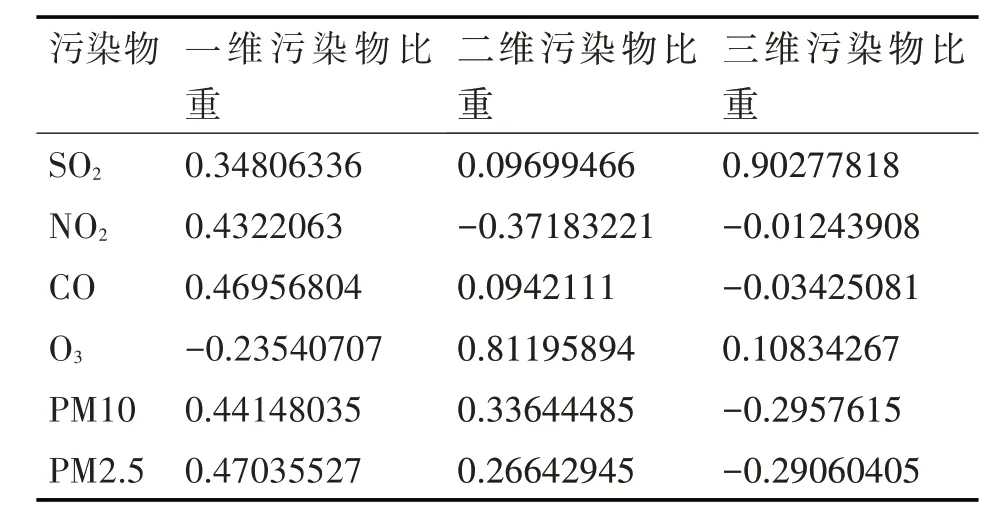
表2 前三维度污染物比重分析

从各维度贡献率中，可以看到，第一维度特征贡献率为58.65238% ；第二维度贡献率为18.100781%；第三个维度贡献率为11.176773%；第四维度贡献率为5.299373%；第五个维度贡献率为4.715392%；第六维度贡献率为2.055301。由六个维度贡献率表明，前3 维度累计贡献率已经达到87.929934%，大于85%，说明这前3 维度特征已经可以反映原始数据特征的绝大部分信息。

由选定的3 个主要特征与污染物变量之间的相关系数。其中，第一维度中所包含的污染物变量中PM2.5 变量的系数最大，为0.47035527，所以可以判定PM2.5对第一维度影响最大，为第一维主因子；第二维度中所包含的污染物变量中O3变量的系数最大，达到了0.81195894，所以可以判定O3对第二维度的影响最大，为第二维主因子；第三维度中所包含的原始变量SO2的系数最大，达到了0.90277818，为第三维主因子，可以判定该区域中主要污染物为PM2.5、O3、SO2。

4.4 关联规则发现验证污染物排放量的关联性

首先对各污染物的数据进行分段，再设置支持度10%，置信度50%进行关联规则关系发现，结果及出现次数、支持度如表3所示。

表3 污染物排放量关联关系表

由 表3 结 果 可 以 发 现，O3与NO2，PM2.5 与NO2、CO、PM10 均具有较强关联性，基于此污染物间关联性结果，比对区域污染企业排放物，可实现污染物的追踪。

5 结语

本文提出了一种基于大数据分析的污染物追踪预测算法。针对获取环保监测数据，首先进行数据预处理，进行数据清洗、数据标准化操作。在关键污染物获取部分应用主成分分析算法对预处理后环保监测数据进行主成分提取，通过累计贡献率，获得关键污染物。针对关键污染物进行关联性发现，挖掘出各污染物之间的关系。最终实现污染物的追踪，可有效提高政府在环境治理中的宏观调控能力。