考虑空间装载约束的智能车间物料调度优化研究*

刘跃强,宋佳佳,张守京

(西安工程大学 机电工程学院,陕西 西安 710048)

0 引 言

在制造业生产加工过程中,生产物流的管理和优化起着重要作用。企业的多品种、小批量的生产制造模式使企业更加依赖对生产物流的管理,物料配送作为生产物流管理的重要环节之一,其关键在于如何合理地调度小车,使工位能够在合适的时间、地点得到合适的物料。优化物料管理、提高物料配送效率,不仅可以保证生产的连续性,还可以减少人力、财力、物力等不必要的浪费。

车辆路径问题和装箱问题是研究空间装载约束下物料调度的两个关键问题。在车辆路径问题(vehicle routing problem,VRP)上,童傅娇等人[1]研究了以工位为中心的优先层级问题;但研究中结合实际问题的约束条件相对较少。ADEBAYO K J等人[2]研究了时间与数量优先级的VRP问题;但其侧重于理论和模型研究,缺少仿真和实验的论证。郭玉洁等人[3]提出了改进的离散鲸鱼优化算法,采用k均值聚类算法进行分类,并引入了邻域搜索策略;但该研究仅局限于算法的改进。胡小建等人[4]分析了物料仓储区与工位之间的关系;但该研究仅提供了一种策略,对求解算法的有效性缺乏验证。蒋增强等人[5]结合混流装配生产线特点,设计了动态周期的物料配送策略;但未考虑到物料需求存在时间窗的变化。

<1)，且各件产品是否为不合格品相互独立．

在考虑空间装载约束的车辆路径问题上,AYOUGH A等人[6]提出了两阶段的模拟退火(SA)算法与空间装载算法,分别构建了三维装载车辆路径问题、带容量的三维装载约束车辆路径问题(three-dimensional loading capacitated vehicle routing problem,3L-CVRP),以及带容量和时间窗的三维装载约束车辆路径问题(three-dimensional loading capacitated vehicle routing problem with time windows,3L-CVRPTW)的数学模型;但该研究仅考虑了三维装载的经典路径优化问题。REIL S等人[7]以最少车辆数目和最小行驶距离为优化目标,解决了打包问题;但该研究侧重于通过提高装载率来降低成本,忽略了工位的需求。吴倩云等人[8]以最短配送路径、最大载重率、最小车辆数目等为优化目标,求解了3L-CVRP问题;但该研究未考虑实际生产过程中存在的紧急插单等扰动现象。KOCH H等人[9]考虑了取送货一体、时间窗和空间装载问题,并引入了先进后出策略(first in last out,LIFO);但该研究主要基于确定环境下的优化问题。PACE S等人[10]设计了一种基于模拟退火和迭代局部搜索的启发式方法;但该研究缺乏与车辆路径问题的有机融合。胡蓉等人[11]研究了二维装载车辆路径问题,设计了天际线填充算法优化装箱;但研究对象仅为大件货物,未考虑货物的三维空间。

为此,笔者对空间装载约束下智能车间物料调度优化问题进行研究。首先,确定配送路径,尽可能在规定服务时间窗内按物料需求程度进行配送;然后,检验配送路径上的物料是否能被装载,选出最佳物料调度方案。

1 问题描述与模型构建

考虑空间装载约束的智能车间物料调度是指,鉴于车间生产过程中存在工序优先、紧急产品插单等情况,在满足时间窗、载重、物料需求紧急度、空间装载等约束条件的基础上,保证运输工具(堆放空间有限)能够装载每一条配送路径的全部物料。

1.1 假设条件

1.1.1 路径约束

1)物料超市约束。只有一个物料超市,是小车出发点和返回点;

2)行程约束。一次配送服务中,小车行驶的总距离始终在最大行驶距离之内;

3)路况约束。小车在配送过程中匀速行驶,不考虑堵塞、排队等待情况;

4)物料订单约束。不进行订单拆分配送;

5)需求紧急度约束。按照物料需求紧急程度来确定工位的优先级;

6)时间窗约束。针对违反物料配送时间窗约束的行为,进行成本惩罚;

7)载重与体积约束。小车所装载物料总重量和总体积均小于小车参数的最大上限。

1.1.2 空间装载约束

1)箱体类型约束。小车配送箱规格只有一种,并且标准物料箱规格均已知;

2)方向性约束。物料箱体的边界总是与配送箱体的边界平行或垂直,且高度方向始终平行于水平面的垂直方向;物料箱体不可倒置,且只存在水平面90°旋转;

3)稳定性约束。物料箱体的接触面积必须达到80%,才能保证其稳定性;

4)可行性约束。物料箱堆叠后所形成的不规则体始终在小车配送箱体内。

1.2 模型构建

笔者以车辆派遣数目最少、总配送成本最低为目标,建立物料调度优化模型。

最少车辆派遣数目如下:

(1)

物料配送的总成本(包括小车派遣成本、行驶距离成本和时间成本)如下:

(2)

式中:C为总配送成本;c1为单辆小车派遣成本;ui为第i个工位的时间惩罚成本;xijk为小车k是否从工位i到达工位j;yik为小车k配送工位i所需物料时是否违反时间窗;dij为各工位间的曼哈顿距离,且dij=dji;η为单位距离的行驶成本。

从节约车间资源的角度出发,笔者提出车辆数目优化偏好型路径规划模型[12],即先优化车辆派遣数目再优化配送路径。

1.2.1 路径约束

针对所有工位进行一次配送服务,表示如下:

(3)

保证到达和离开工位的小车相同,表示如下:

(4)

所有小车均从物料超市出发,最后再返回出发点,表示如下:

x0ik=xi0k,∀i∈N,∀k∈K;

(5)

物料配送的次序按照工位对物料需求的紧急程度进行排序,表示如下:

(6)

式中:Ii为第i个工位对物料需求紧急度高低的优先级参数。

若第i工位物料需求紧急程度Ii高于第j工位物料需求的紧急程度Ij,即i工位需求的最佳时间小于j工位需求的最佳时间,则先将物料配送至i工位,再配送至j工位。

针对违反时间窗的行为,进行成本惩罚,表示如下:

(7)

式中:α,β为早于或晚于工位服务时间窗到达的惩罚参数;si为到达第i个工位的时间点;ati,bti为工位服务时间窗上限和下限。

1.2.2 装箱约束

标准物料箱体边界总是平行或正交于配送箱体边界,表示如下:

(8)

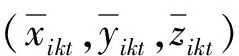
标准物料箱可以进行水平方向90°旋转,但不可倒置,表示如下:

(9)

式中:hik为小车k上第i工位所需标准物料箱的高度。

堆叠后的标准物料箱尺寸不可超出箱体最大边界尺寸,表示如下:

(10)

式中:Lk为小车k配送箱体的长度;Wk为小车k配送箱体的宽度;Hk为小车k配送箱体的高度。

笔者提出假设:任意两物料箱在同一车厢存在重叠摆放现象,即A(j,m)与物料箱Eikt放在同一配送箱中的其他箱子集合[13]。

标准物料箱在空间内部是不重叠的,表示如下:

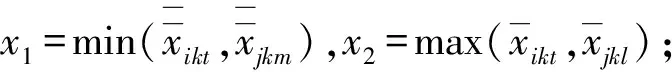
x1≤x2或y1≤y2或z1≤z2

(11)

式中:(x1,y1,z1)为标准物料箱的最小右后上角坐标;(x2,y2,z2)为标准物料箱的最大左前下角坐标。

重叠箱体平面投影图如图1所示。

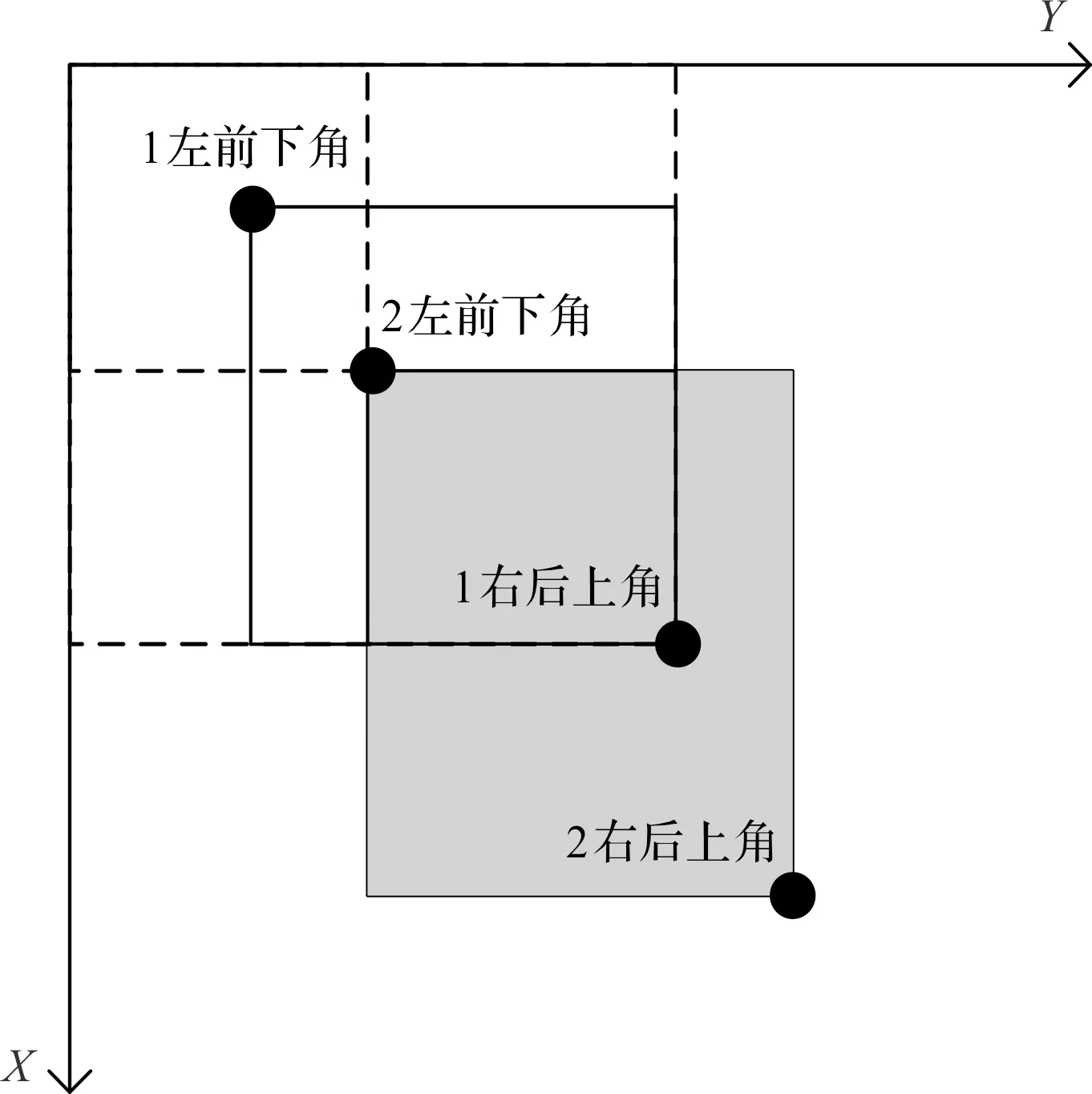
图1 重叠箱体平面投影图

图1中:两个标准物料箱在X-Y水平面投影—阴影区域表示重叠部分;如果箱体不重叠,则水平面投影也无阴影区域。

标准物料箱的重叠存在支撑面约束,表示如下:

∑(x1-x2)(y1-y2)≥flikt·wikt·hikt,

x1>x2,y1>y2;

(12)

式中:f为支撑面约束的参数。

2 两阶段混合算法设计

笔者设计了一种鲸鱼算法(WOA)和SA相结合的两阶段混合算法,即改进鲸鱼优化算法(WOA-SA)。

两阶段混合算法求解流程图如图2所示。

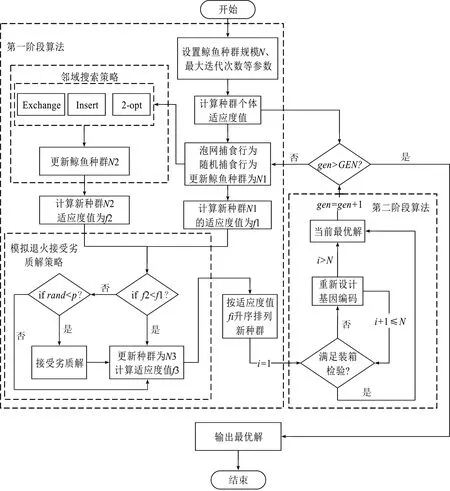
图2 两阶段混合算法求解流程图

第一阶段,以WOA为基本框架求解路径优化问题;第二阶段,利用装箱算法检验物料的可装载性,以确保路径是可行的。

2.1 改进鲸鱼优化算法设计

笔者对鲸鱼算法中包围猎物、发起泡泡网攻击猎物、再捕食猎物等行为进行适当删改和再定义。

2.1.1 编码与解码

将鲸鱼算法中连续性变量转换成离散化变量,即对工位进行整数编码。假设某车间工位为n={1-1*,2-2*,3-3*,4-4*,5-5*,6-6*,7-7*,8-8*,9-9*,10-10*}。其中,*表示工位所需的物料。某一次工位配送顺序为1-2-3-4-5-6-7-9-8-10,按照重量、容积等约束的限制可能需要3辆小车进行配送,则解码成0-1-1*-2-2*-3-3*-4-4*-0,0-5-5*-6-6*-7-7*-0,0-9-9*-8-8*-10-10*-0。其中,0为物料超市。

2.1.2 鲸鱼位置更新

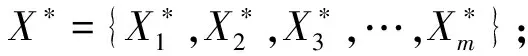
2)泡泡网捕食。该过程是鲸鱼针对猎物的局部搜索过程。发起泡泡网攻击的捕食行为存在两种方式:收缩包围机制和螺旋吐泡机制,即鲸鱼以一定概率选择捕食方式,从而更新鲸鱼个体位置。假设现有工位配送顺序为x={x1,x2,x3,x4,x5,x6,…,xn},则鲸鱼个体位置更新的操作,如下:

(13)

式中:xn为第n个工位;p为捕食方式的概率;

3)随机搜索捕食。鲸鱼以反转、插入操作方式更新位置,从而靠近猎物。若更新后的种群适应度值C2低于原种群适应度值C1,则保留更新后的工位配送顺序;反之,则工位配送顺序保持不变,如下:

(14)

式中:C2为种群更新后的个体适应度值;C1为种群更新前个体适应度值。

2.1.3 邻域搜索策略

为了增强算法的空间搜索能力,笔者将模拟退火接受劣质解思想与邻域搜索策略相结合,提出了随机交换算子(Exchange)、2-opt算子、随机插入算子(Insert)相结合的邻域搜索策略。

1)Exchange。随机选择两个工位点进行点对点交叉操作;

2)Insert。随机选择两个工位点进行前后的插入操作;

3)2-opt。随机选择两个工位点,并对两工位点之间所有工位进行反转操作。

2.1.4 接受劣质解准则

Metropolis接受准则是模拟退火算法的核心,旨在筛选出优质解,并控制接受劣质解可能性。准则表示如下:

(15)

式中:P为接受劣质解的概率;T为模拟退火的温度;f1为邻域操作前的个体适应度值;f2为邻域操作后的个体适应度值。

关于P值求解涉及退火过程,表示如下:

Tgen+1=Tgen×s

(16)

式中:gen为算法迭代次数;Tgen为第gen代的模拟退火温度;s为冷却因子。

2.2 装箱检验算法设计

2.2.1 物料装载策略

假设所有物料只能从箱体正上方进入,在不超出配送箱体尺寸的情况下,优先对尺寸完全相同的标准物料箱进行打包,然后将包装后的物料箱与未包装的物料箱按照摆放策略统一装箱。

2.2.2 空间摆放策略

1)“先左后右”优先级策略。将标准物料箱摆放在配送箱体的最左下端位置,然后进行选择性堆叠。当左侧空间不足时,进行右侧空间摆放;

2)“自下而上”优先级策略。将第一个标准物料箱摆放至最左侧空间后,优先考虑第二个标准物料箱摆放其上层空间。

2.2.3 摆放规则

如1.1节假设条件已描述空间可行性、支撑面稳定性、旋转方向性等约束,故笔者不再赘述。

2.2.4 坐标确定方法

坐标点的确定是通过保留每个标准物料箱的3个关键顶点以选择出合适的摆放点。

空间摆放策略如图3所示。

图3 空间摆放策略

图3中:摆放第一个物料箱,并记录1、2、3号点共3个关键点坐标,且存在优先级关系依次为:1-2-3;摆放完成后,记录4、5、6号点循环上述操作。

如果配送路径上的物料不能够被完全装载,则选取次优配送路径进行装箱检验,直至选出满足条件的配送路径。

2.3 WOA-SA混合算法实现步骤

根据上述设计的WOA-SA和空间装载算法可知,两阶段算法的主要步骤如下:

1)鲸鱼种群初始化,种群规模为N、最大迭代次数MAXGEN等参数;

2)计算鲸鱼种群的个体适应度值;

3)泡泡网捕食行为,通过两种泡泡网捕食行为来更新鲸鱼群的位置。当p<0.5时,鲸鱼个体螺旋吐泡攻击猎物;当p≥0.5时,鲸鱼个体进行收缩包围攻击猎物;

4)随机捕食行为,通过反转和插入操作再次更新鲸鱼群位置并计算适应度值,选出较优的鲸鱼群位置;

5)邻域搜索策略,通过Exchange、Insert和2-opt操作增加邻域结构和邻域解;

6)模拟退火接受劣质解策略,计算邻域搜索操作后的个体适应度值并以一定概率接受劣质解,更新鲸鱼种群的位置;

7)空间装载检验算法,对优化后鲸鱼种群个体按优劣顺序逐一进行检验,筛选出符合约束条件的最优解;

8)判断gen是否满足最大迭代次数MAXGEN,如果满足条件,则跳出此次循环;反之,跳转至Step3,继续迭代;

9)输出全局最优解,记录最优物料调度方案。

3 实例仿真与分析

笔者实现两阶段算法的仿真环境如下:操作系统为Windows 10家庭中文版,计算机内存为4 GB,CPU型号为Intel Core i5-7200U,算法编程软件为MATLAB 2019a。

3.1 实例数据与参数设置

笔者以文献[2]1469中车间数据及算法参数选择为基础,结合某车间物料信息并对物料重量(G)进行调整。

考虑装载约束的车间物料配送过程示意图如图4所示。

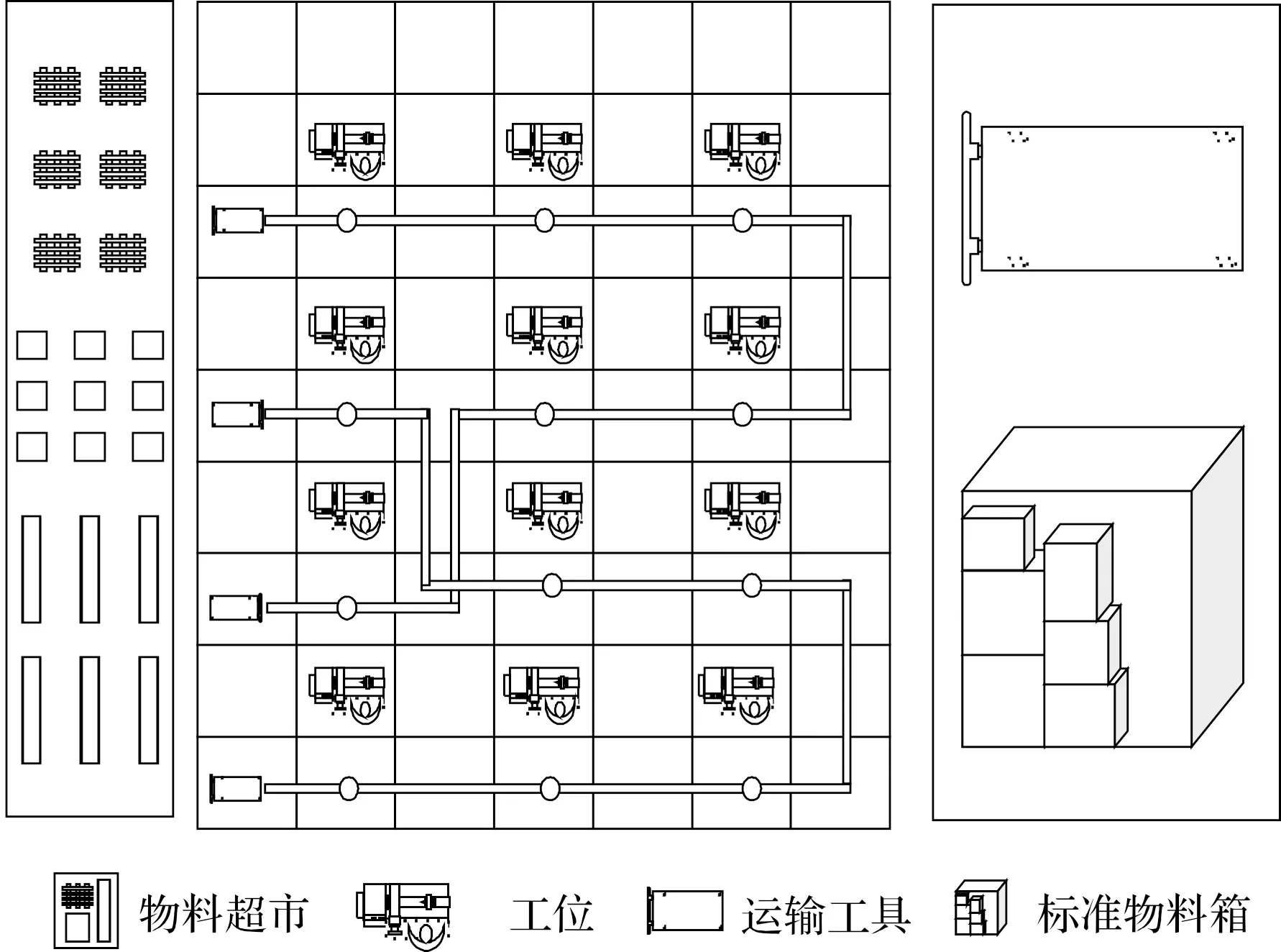
图4 考虑装载约束的车间物料配送示意图

已知配送小车配送箱体的长度为0.75 m、宽度为0.8 m、高度为0.75 m、最大负载为100 kg,标准物料箱规格有8种。

标准物料箱规格及需求工位如表1所示。

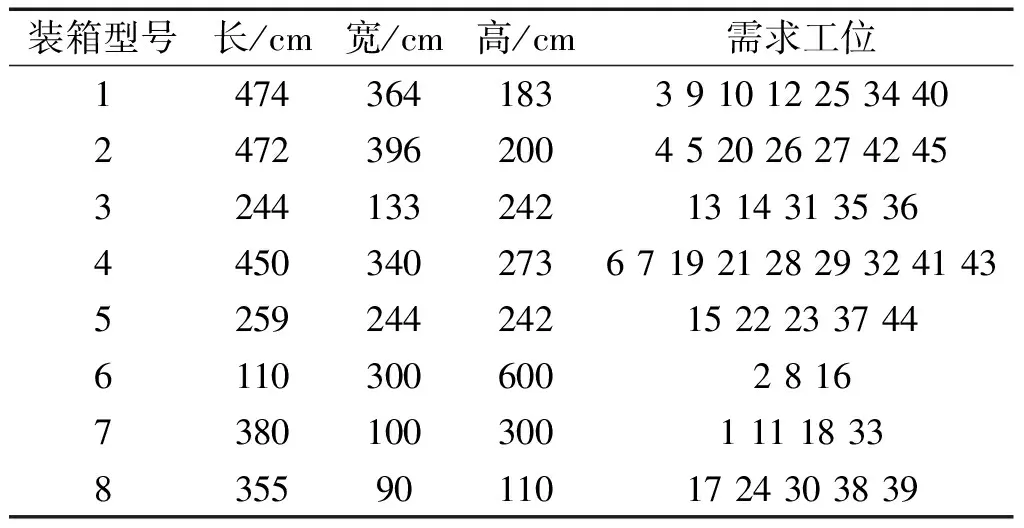
表1 标准物料箱规格及需求工位

工位所需物料重量如表2所示。

表2 工位所需物料重量表

WOA-SA参数设置:种群规模N=100,最大迭代次数MAXGEN=500,模拟退火温度为1 000 ℃;早于时间窗到达工位的惩罚系数为60,晚于时间窗到达工位的惩罚系数为900;小车的行驶速度为5 km/h,小车的固定使用成本为250元,单位距离的行驶成本为1.5元/km。

综合以上数据,笔者将通过实例来验证改进算法的有效性,并分析不同约束条件下求解带时间窗有能力限制的车辆路径问题(CVRPTW)的结果。例如,工位满意度是指按物料需求程度进行配送,且在规定时间窗内送达工位的数量占总工位数量的比率。

3.2 模拟退火算法参数分析

模拟退火算法接受劣质解的概率影响着WOA的寻优能力,冷却因子是关键参数之一,故笔者针对模拟退火算法冷却因子取值进行对比分析。

经调研可知,冷却因子s在[0.7,0.99]范围内进行不等距取值,以最佳配送成本(bestC)、平均配送成本(avC)为衡量指标并运行算法10次,模拟退火算法参数对比分析如表3所示。

表3 模拟退火算法参数对比分析

由表3分析可知:当s=0.80时,算法求解的最佳配送成本和平均配送成本均为最优。s值过大,不易接受劣质解;s值过小,会出现淬火现象,错失优质解。故取0.80为最佳值。

3.3 对比实验与分析

为了更好地验证WOA-SA混合算法求解CVRPTW的能力,笔者将其与引入交叉变异算子的SA[14]、WOA、遗传算法(genetic algorithm,GA)[15]和引入精英策略的混合粒子群算法[16](particle swarm optimiz-ation and genetic algorithm,PSO-GA)进行实例求解的横向比较(算法参数如第3.1节、第3.2节中的表述所示);以最佳配送成本(bestC)、平均配送成本(avC)和平均耗时(avT)为衡量指标,采用不同算法分别运行10次。

算法求解情况对比结果如表4所示。

表4 算法求解情况对比

不同算法求解的成本曲线图如图5所示。

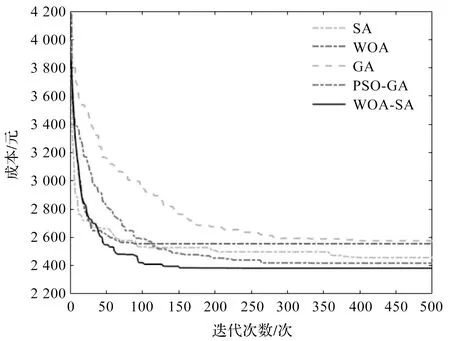
图5 不同算法求解的成本曲线图

从表4中可看出:WOA-SA求解的成本最优,相对其他算法,其计算消耗的时间是可以接受的。

图5中:笔者设计的改进算法求解CVRPTW问题的成本最低,且曲线收敛速度较快,相对其他算法具有一定的优越性。

笔者研究不同约束条件的CVRPTW问题,以车辆派遣数目(num)、最佳配送成本、平均配送成本、工位满意度(JS)、平均工位满意度(avJS)为衡量指标进行10次仿真实验。

不同约束的CVRPTW问题结果对比如表5所示。

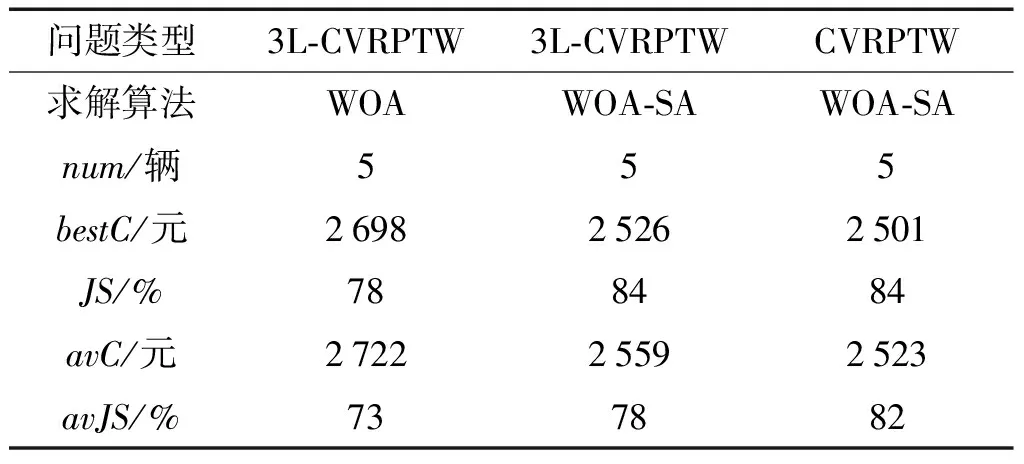
表5 不同约束的CVRPTW问题结果对比

笔者选取10次仿真实验的最优解进行对比分析,采用混合算法求解不同约束CVRPTW问题,结果如图6所示。

图6 混合算法求解不同约束CVRPTW问题

图6(a)中:分析曲线波动可知,WOA收敛速度较快,但易陷入局部最优;WOA-SA混合算法收敛速度相对缓慢,但可得出全局较优解。

表5中:两者最佳配送成本相差172元,工位满意度相差6%。就平均结果而言,WOA-SA混合算法的平均成本相对节约了6%,平均工位满意度提高了5%,证明了混合算法求解多约束问题仍具有较好的寻优能力。

由于WOA-SA混合算法拥有较好的寻优性,笔者研究了空间装载约束条件对求解考虑物料需求紧急度的CVRPTW问题的影响。

图6(b)中:采用WOA-SA改进算法求解3L-CVRPTW问题时,曲线收敛速度较快,但最优配送成本略高。

从表5中可以看出:3L-CVRPTW问题的求解结果无论是最佳配送成本、平均配送成本,还是平均工位满意度都差于CVRPTW问题的求解结果。因此,当路径上的所有物料不能被完全装载,将改变物料配送次序,增加了配送成本。

由改进后的WOA-SA混合算法求3L-CVRPTW问题的最优配送路径可知:配送过程的行驶成本为1 256元,车辆使用成本为1 250元,时间惩罚成本为20元。

最优物料配送结果如表6所示。

表6 最优物料配送结果

4 结束语

在生产过程中,装配制造车间会受到多种因素干扰,因此,笔者建立了多约束物料调度数学模型,并采用两阶段混合算法得出了物料调度优化方案。

研究结果表明:

1)将装载问题与车间物料配送问题有机融合,提出了WOA-SA混合算法,并验证了模型的可行性及算法的有效性;

2)考虑车辆空间装载能力和物料需求紧急度等约束条件,提高了工位服务满意度及配送的准确度;

3)构建了以总配送成本为次目标的车辆数目偏好型车辆路径问题,利用两阶段混合算法使成本降低了172元,工位服务满意度提高了6%。

在目前的研究中,尚未考虑LIFO原则。今后,笔者将结合装载问题,探究小车电量限制、车间道路堵塞以及不确定环境下物料的调度问题。