基于蜻蜓翅几何及刚度相似性的仿生扑翼结构

贺媛媛，杨炫，韩慧，王琦琛，张航

北京理工大学 宇航学院，北京 100081

微型飞行器现如今处于高速发展的阶段，在军事和民用上被运用得越来越广泛。按照飞行器的布局形式与飞行原理可以将微型飞行器分为固定翼微型飞行器、旋翼微型飞行器和扑翼微型飞行器［1］。近年来，通过对鸟类及昆虫等飞行生物的观察、试验以及数值仿真研究，仿生扑翼飞行器受到越来越多学者的关注［2-3］。相对于固定翼飞行器与旋翼飞行器，大量扑翼飞行器具有气动效率高、机动性好、能垂直起降并保持悬停等优点，但同样存在机械系统复杂等缺点。针对扑翼飞行器的弊端，英国克兰菲尔德大学的Guo 等［4］提出了扑旋翼的概念，结合扑翼与旋翼的技术特点，通过安装一对中心对称的翼使得扑翼在上下拍动的同时在两侧翼面上产生一对力偶，带动扑翼实现旋转，在保留扑翼优点的同时使得结构较为简单，能耗降低。

目前，世界上微型扑翼飞行器与扑旋翼飞行器的研究主要集中在实现仿生拍动的驱动机构设计方面［5-6］和对飞行器气动特性进行的数值模拟和试验验证方面［7-13］。Keennon 等［14］对扑翼构型进行研究，分析翼膜材料、扑翼展弦比等对于升力产生的影响。Chen 等［15］通过对于扑翼形态和惯性参数的改变探究其对于飞行器飞行性能的影响。周超等［16］基于扑旋翼飞行器的发展，提出了扑旋翼增升设计。而在对昆虫翅翼的研究方面，蜻蜓翅翼由于薄且轻但在拍动、滑翔和悬停等飞行状态下的稳定性和承载能力都极其优异因而受到研究者们的广泛关注［17-19］。宏观上，蜻蜓翅翼由翅脉和翅膜组成［20］。翅膜轻薄，为透明状，使蜻蜓飞行时产生空气动力，翅脉纵横交错，主要起到支撑作用。从微观角度来看，翅膜的成分为结构性蛋白，包括背部层、中间层和腹部层［21］。表面不同部位微观结构的不同有效减少了蜻蜓飞行过程中的阻力。此外，部分学者还对翅翼的材料和力学性能进行了研究。Kempf［22］使用纳米压痕技术发现翅脉的弹性模量为（2.9±0.8） GPa，翅膜的弹性模量为（1.5±0.5） GPa，且前翅的弹性模量和硬度大于后翅。张金［23］和潘春祥等［24］分别对蜻蜓翅翼的前缘脉、径脉和后缘脉进行了纳米力学性能研究，得到了蜻蜓翅翼翅脉弹性模量和纳米硬度沿翅翼展向的变化关系。

在目前的电机电池等部件尺寸和重量的条件限制下，可实现飞行仿生扑翼微型飞行器的尺度和重量都比昆虫大一个数量级，而到目前为止，仿生研究实际上都是在模仿昆虫翅的拍动模式，对昆虫翅本身而言，无论是按照几何相似仿制昆虫翅，或是制作简化外形和结构的扑翼，尚无统一而成熟的设计制作方法。本文基于自然界中不同尺度下昆虫翅翼抗弯刚度与几何形态参数的关系，并依据蜻蜓翅刚度实验结果得到其展向抗弯刚度与展长的关系，建立了适用于仿蜻蜓翅的扑翼设计刚度相似性准则。首先采用拓扑优化方法建立仿生扑翼构形分布，进而根据刚度相似性准则确定具体结构的参数，设计制作出仿蜻蜓翅扑翼，最后通过扑旋翼模型试验验证了基于刚度相似性研制的扑翼能够明显增升并提高效率。

1 基于主成分分析法的昆虫翅翼刚度

1.1 主成分分析法

主成分分析法是一种多元统计方法，用于实现多个变量之间相关性的考察，基于对各个变量构成的矩阵进行研究，分析其内部关系，将多个存在相关性、阐述不同信息的指标转换为尽可能少的不相关的综合指标［25］。

主成分分析法的基本步骤如下：

1） 假定有n个样本，每个样本共有p个变量，构成一个n×p阶的数据矩阵：

2） 计算相关系数矩阵：

式中：rst为原变量xs与xt的相关系数（s，t=1，2，…，p），且rst=rts，其计算公式为

3） 计算相关系数矩阵R的特征根与特征向量，确定主成分。由式（4）所示的特征根方程式可求得p个特征根λs：

式中：I为单位矩阵。

按其大小顺序排列为λ1≥λ2≥…≥λp≥0。由式（4）可知，每一个特征根对应一个特征向量es。

4） 计算主成分贡献率，根据累计贡献率确定主成分个数。

主成分zs的贡献率为

累积贡献率为

主成分分析中在确保损失的信息量尽可能少的前提下选取尽量少的m个主成分进行综合评价，通常选择累计贡献率的特征值对应的第1，2，…，m(m≤p)个主成分。

5） 计算主成分载荷。

原变量xt在诸主成分z1，z2，…，zm(m≤p)上载荷的计算公式为

6） 记x1，x2，…，xp为原变量指标，各主成分z1，z2，…，zm为新变量指标。各主成分的得分为

1.2 昆虫翅翼刚度分布

昆虫翅翼在飞行中由于气动力、惯性力和翼结构弹性力的耦合作用产生被动的气动弹性变形，虽然不同尺寸和类型的昆虫翅外形和脉结构有所差异，但整体具有相似的刚度分布特性。

部分昆虫的翅长度、弦长、面积、昆虫质量和翅70% 展长处的展向截面抗弯刚度EI 数据如表1 所示［26］。从表1 中可以看出，随着翅翼长度、翅翼弦长、翅翼面积和昆虫质量的增加，昆虫翅翼展向抗弯刚度逐渐增大。为了得到各个参数的综合指标对扑翼展向抗弯刚度的影响，采用主成分分析法进行分析，通过不同尺度下飞行生物翅翼刚度与几何形态参数之间的关系确定刚度相似性准则。

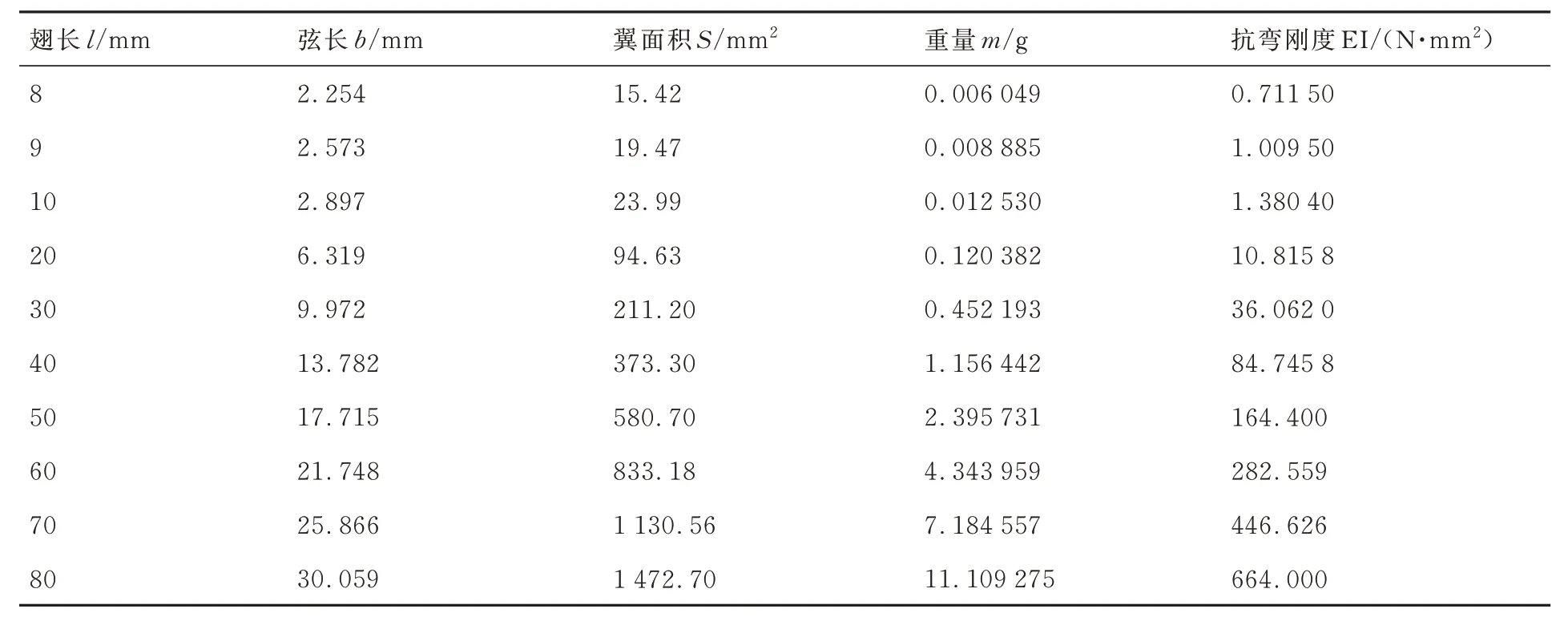
表1 部分昆虫翅尺寸和重量及翼展向抗弯刚度数据［26］Table 1 Size， weight and bending stiffness of some insect wings［26］

以昆虫翅翼翅长、翅翼弦长、翅翼面积和昆虫质量为参数，探究4 者的综合指标对扑翼展向抗弯刚度的影响。首先，取表1 前4 列的数据（翅长、弦长、翼面积、重量）构成如式（1）所示的10×4 的数据矩阵，标准化处理翅长、弦长、翅翼面积和质量的相关数据，通过主成分分析法计算得到相关系数矩阵为

通过计算得到特征值及各个主成分的方差贡献率如表2 所示。由表2 可知，第1 主成分的累计贡献率高于85%，故只需求出第1 主成分即可。对于特征值λ1=3.884 6，求出其特征向量，再计算得到各变量在主成分上的载荷，则主成分z1得分表达式为

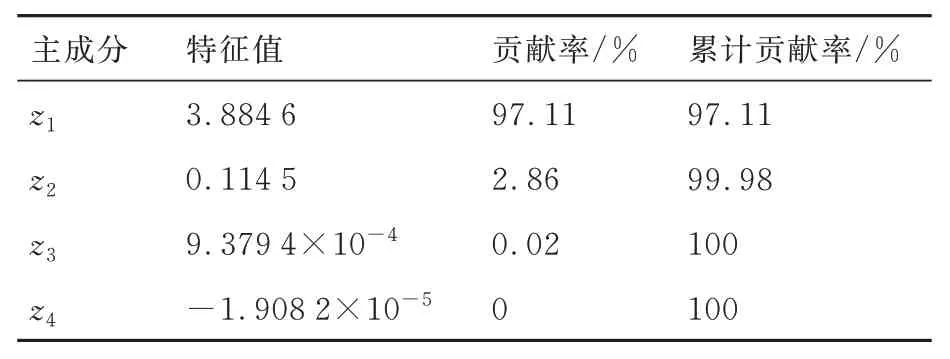
表2 特征值及主成分贡献Table 2 Eigenvalues and principal component contribution

采用对数函数对由翅长、弦长、翅翼面积和质量组成的第1 主成分与昆虫展向抗弯刚度的数据进行拟合，得到由翅长、弦长、翅翼面积和质量组成的综合指标z1与昆虫展向抗弯刚度EI 之间的关系式为

2 蜻蜓翅刚度实验

蜻蜓具有前飞、滑翔、倒飞、垂直飞行和悬停等多种飞行性能，翅翼拍动频率低，飞行速度快，在有翼昆虫中的综合飞行性能最优，但却是仿生飞行器实现飞行最具有挑战的模式。蜻蜓翅展弦比相对其他昆虫大，在飞行中会发生大幅度的弯曲变形和扭转变形，刚度分布和大小对飞行性能的影响大。以图1 所示的黄蜻为例对蜻蜓翅翼的展向抗弯刚度进行进一步分析。

图1 黄蜻Fig.1 Yellow dragonfly

蜻蜓翅样件几何形态参数测量结果如表3 所示。由于蜻蜓后翅较多采集样件破损，因此只基于蜻蜓前翅进行刚度测试实验。同一蜻蜓的2 个前翅的长度和最大弦长基本相同。

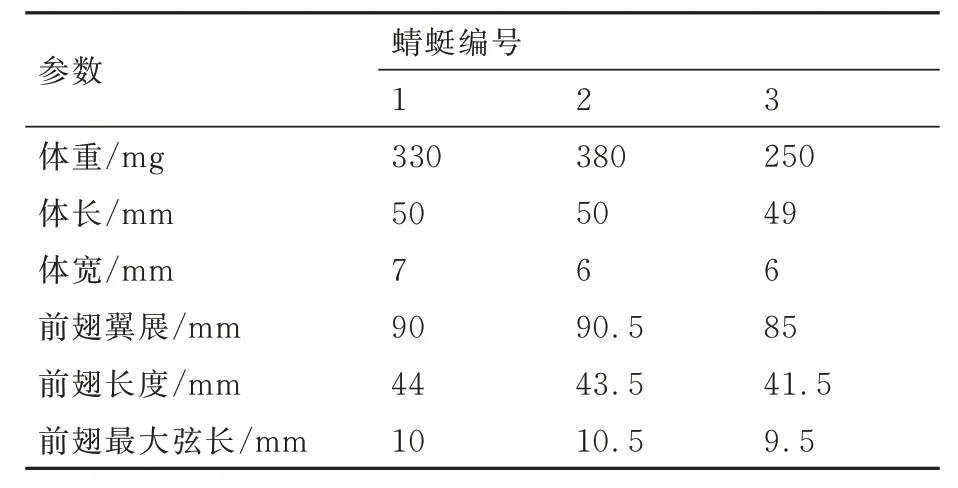
表3 蜻蜓几何形态参数测量结果Table 3 Results of dragonfly geometric morphological parameters measurement

对蜻蜓前翅进行刚度实验，采用悬臂梁弯曲试验方法测量其抗弯刚度。测量黄蜻翅翼抗弯刚度方法如图2 所示。将蜻蜓翅根粘接在固定支座上，再将质量块通过细线连接在翅脉上，测量加载荷点处的位移。

图2 蜻蜓翅翼刚度测量Fig.2 Measurement of stiffness of dragonfly wings

根据测量的位移结果，结合式（12）可计算得出蜻蜓翅在展向不同截面的抗弯刚度。为提高精确度，同一位置反复施加不同大小载荷得到平均值，加载力的大小以线弹性变形为准则，加载力和位置及计算结果如表4～表9 所示。

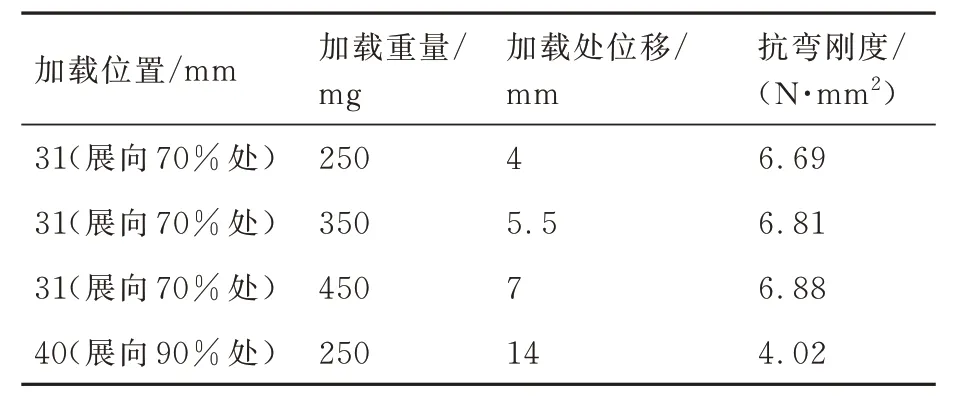
表4 1 号蜻蜓右翅刚度实验测量结果Table 4 Experimental measurements of right wing stiffness of Dragonfly 1

式中：F为翅所受的加载力；L为翅根到加载截面的距离；δ为加载点处的位移，如图2（a）所示。

表4 和表5 的测量结果显示，1 号蜻蜓左右两翅在相同展向位置处的抗弯刚度存在较大差异，这是因为在实验之前将1 号蜻蜓左右两翅同时从蜻蜓上摘下，导致做完右翅实验时，左翅随着时间流逝变干，刚度增大，相同载荷下位移变小，这说明翅翼的刚度与生物体的活性有关，因此后续的实验中没有同时摘下翅翼，而是在做完一只翅翼的试验后再摘下另一只翅翼。

表5 1 号蜻蜓左翅刚度实验测量结果Table 5 Experimental measurements of left wing stiffness of Dragonfly 1

由于1 号蜻蜓左翅是在翅翼活性降低刚度增大的情况下测得的，误差较大，所以将忽略表5 测得的1 号蜻蜓左翅刚度，不将其计入后续数据处理。根据表4 及表6～表9 所示的蜻蜓翅在不同展长处加载的位移实验结果，可以得出如图3（a）所示的蜻蜓翅不同展长处载荷大小与位移的变化关系。结果显示，在相同展长位置施加载荷时，载荷与位移基本呈线性关系，说明实验是在蜻蜓翅的线弹性变形范围内，满足式（12）的条件。因此，根据式（12）计算可得表4 及表6～表9所示的各蜻蜓翅的刚度结果。取上述实验结果的平均值，得到如图3（b）所示的各蜻蜓翅在不同展向位置抗弯刚度。

图3 蜻蜓翅刚度实验结果Fig.3 Results of dragonfly wing stiffness experiments

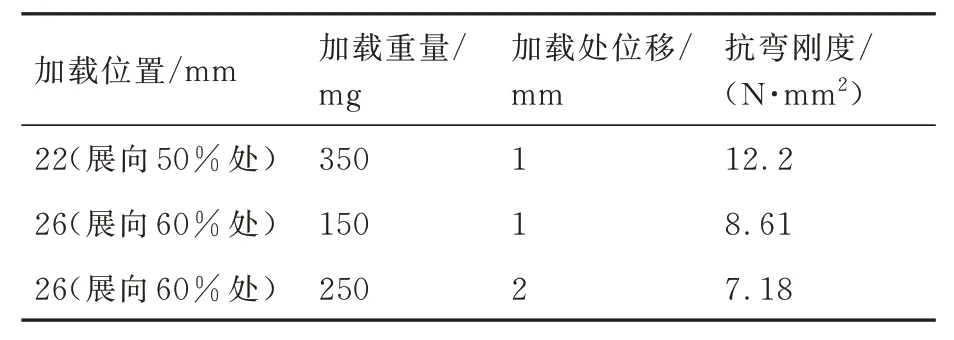
表6 2 号蜻蜓左翅刚度实验测量结果Table 6 Experimental measurements of left wing stiffness of Dragonfly 2

表7 2 号蜻蜓右翅刚度实验测量结果Table 7 Experimental measurements of right wing stiffness of Dragonfly 2

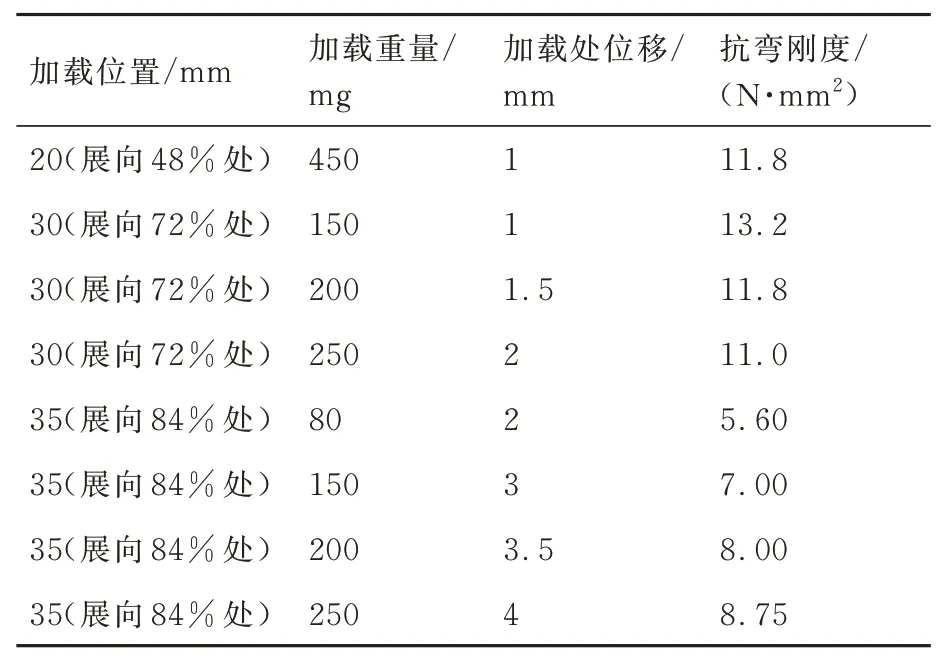
表8 3 号蜻蜓左翅刚度实验测量结果Table 8 Experimental measurements of left wing stiffness of Dragonfly 3

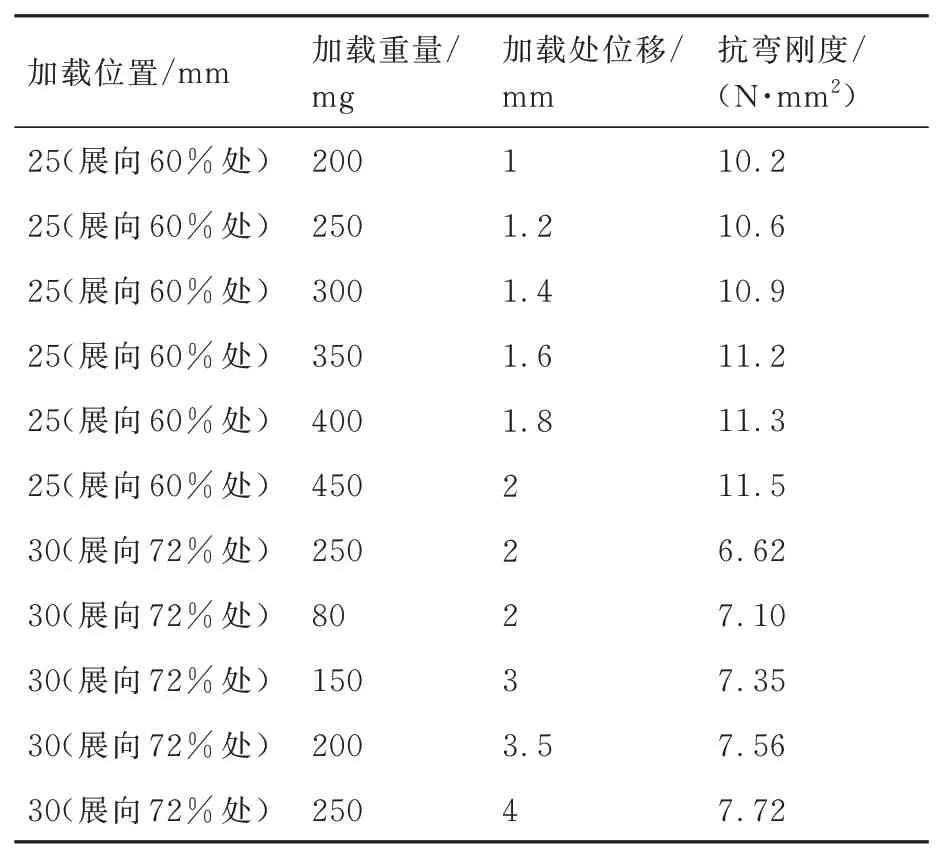
表9 3 号蜻蜓右翅刚度实验测量结果Table 9 Experimental measurements of right wing stiffness of Dragonfly 3

由图3（b）可见，蜻蜓翅翼的抗弯刚度从50%展长至90%展长处逐渐减小。目前的研究发现蜻蜓翅翼刚度分布从翼根到翼尖大致呈线性关系变化［27］，结合图3（b）可以得出蜻蜓翅刚度与展长关系的拟合计算式：

式中：E为翅材料的弹性模量；Ii为扑翼展长i×10%处的截面惯性矩（i取0，1，…，10）；m为Ii沿展长变化的线性一次函数的斜率；n为线性一次函数的截距。

3 基于刚度相似性的扑翼结构优化设计

3.1 扑翼结构拓扑优化

蜻蜓翅翼上具有很多的微观结构，翅脉纵横交错，即便采用3D 打印加工方法也难以做到对其翅脉分布完全复制或仿制，也不能保证其刚度和质量分布与蜻蜓翅的相似性，所以首先采用拓扑方法对仿生扑翼结构布局进行优化，对仿蜻蜓翅的扑翼结构采用壳单元建立的有限元模型如图4 所示。蜻蜓由于前缘脉是蜻蜓翅承力的主要部件，翅脉直径相对大，是不可或缺的悬臂梁，因此将前缘脉位置（即图中蓝色区域）模型定义为非设计域，图中紫色部分为结构设计域。蜻蜓在实际飞行中的气动力变化复杂，此处简化为垂直于翅翼表面的均布载荷，其合力为蜻蜓体重的一半。另外，在翅翼根部设置六自由度约束，模拟蜻蜓翅与体的连接。

图4 蜻蜓翅翼平面结构有限元模型Fig.4 Finite element model of plane structure of dragonfly wing

扑翼需要具有一定的承载能力以承受飞行过程中产生的气动载荷，这就对扑翼的刚度有所要求。此外，减重是扑翼设计一直致力的目标。因此，建立如式 （14）所示的结构拓扑优化数学模型，其中，设计变量为各个单元的伪密度，优化目标为结构节点力下所做的功，约束条件为材料保留比。

式中：xα为第α个单元的伪密度；C为结构节点力F所做的功；F为结构节点力向量；U为结构节点位移向量；M为结构质量；M0为结构原质量；f为材料保留比，表示优化后结构保留的材料占原结构材料的比例；K为结构整体刚度矩阵；xmin为防止刚度矩阵奇异引入的单元伪密度最小值。其中，C值越小代表结构刚度越大。

对于如图4 所示的仿蜻蜓翅扑翼平面结构有限元模型，利用ABAQUS 软件中的Optimization模块进行结构拓扑优化，插值模型罚系数取p=4，材料保留比分别取f=0.189～0.191，0.199～0.201，0.219～0.221，0.259～0.261，0.299～0.301，得到的结构拓扑优化结果如图5 所示。

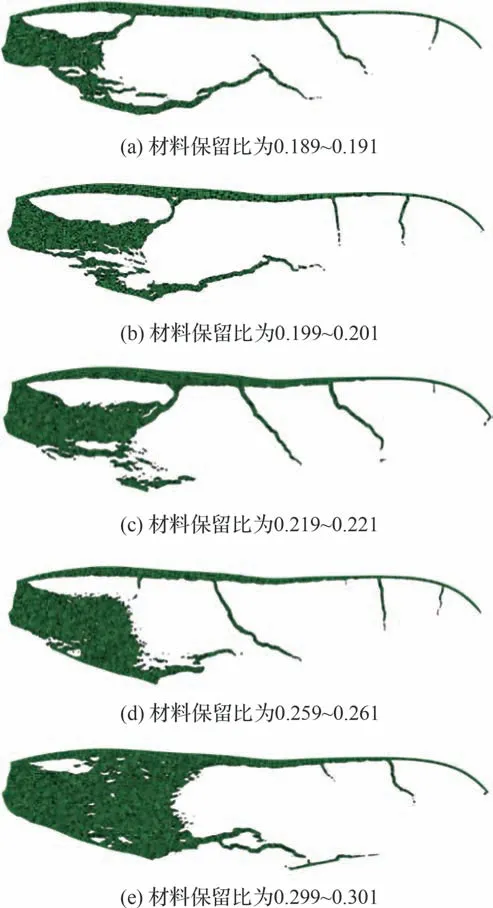
图5 不同材料保留比设置下的结构拓扑优化结果Fig.5 Results of structural topology optimization with different settings of material retention ratio

从拓扑优化结果可见，对应不同材料保留比的扑翼结构都具有较为清晰且与蜻蜓翅相似的脉络分布，翼根处的脉络密度高，材料保留量大，是由于该处应力集中并承受全部载荷。在扑翼前缘梁处和后缘中部延伸出多条脉络，将分布载荷传递到翼前梁。

在对扑翼结构进行拓扑优化过程中，由于将复杂的气动力简化为垂直于翅翼表面的均布载荷，忽略了前缘涡的增升作用，因此导致拓扑优化的模型前缘脉络细节缺失，与蜻蜓翅脉有差别。而蜻蜓翅具有更多细致分布的主脉和从脉，如图6 所示，基于蜻蜓翅的脉络分布，在拓扑优化的有限元模型上添亚前缘脉、横脉和中部主脉等缺失的细节，得到仿蜻蜓扑翼的基本结构模型如图7 所示。

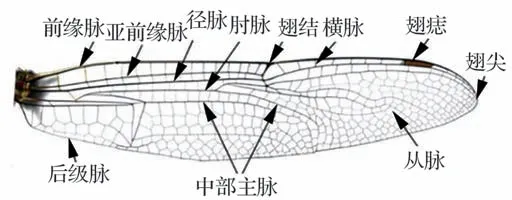
图6 蜻蜓翅翼样本及脉络分布Fig.6 Dragonfly wing samples and vein distribution

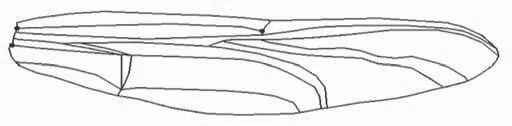
图7 仿蜻蜓简化翅翼设计模型Fig.7 Simplified design model of dragonfly wing

3.2 基于几何相似性的扑翼设计

基于上述扑翼的结分布模型，可进一步针对各翼脉细节进行仿生设计分析。如图8 所示，蜻蜓翅脉为环形空心结构，根据文献［28］中对蜻蜓翅的尺寸测量，取翅长度为47.6 mm，将翅脉截面简化为外围半径为0.067 5 mm、厚度为0.025 mm 的圆环，翅膜厚度为0.004 mm。鉴于加工技术的限制，将该翅脉截面简化为相同刚度的梁单元模型。根据计算得出，在材料参数不变的情况下，半径为0.064 7 mm 的圆形截面梁单元模型具有和空心翅脉相同的刚度。

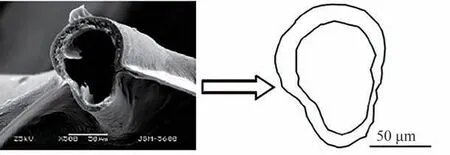
图8 蜻蜓翅脉的横截面及其几何构型［28］Fig.8 Cross section of dragonfly wing veins and its geometric configuration ［28］

进而可根据需要设计的微型仿生飞行器的扑翼尺度对仿蜻蜓翅扑翼模型按几何相似比例放大。以半展长160 mm 的扑翼为例，翼展放大比例为3.36（=160/47.6），在原始模型中对每个截面的展弦比按照3.36 倍进行放大，按照原始模型脉络走向与趋势连接新的点形成放大后的翅翼脉络，以此保持原始模型的翅翼外形结构、脉络分布不变，同时将模型中翅脉的截面半径放大为0.217 5 mm（=0.064 7×3.36）。考虑到加工因素，将翅脉截面设计为矩形，在保持截面积不变的情况下，选定截面尺寸为0.4 mm×0.37 mm，得到按几何相似性设计的扑翼模型如图9 所示。

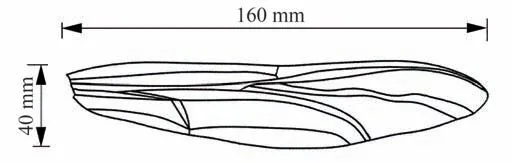
图9 基于几何相似性放大的扑翼模型Fig.9 Flapping wing model based on geometrical similarity amplification

3.3 基于刚度相似性的扑翼设计

3.3.1 扑翼刚度分布

在设计和制作时需根据所采用的材料参数和尺寸限制按照刚度相似性准则确定扑翼模型中各梁元的刚度，以同样的扑翼模型为例，其半展长、最大弦长、表面积和设计飞行器重量分别为：l=160 mm，b=40 mm，S=5 000 mm2，m=30。根据建立的刚度相似性准则式（10）及式（11），再结合式（13）得到该扑翼模型展向抗弯刚度随展长的变化为

根据式（15）可计算出扑翼在不同展长处的抗弯刚度如表10 所示。

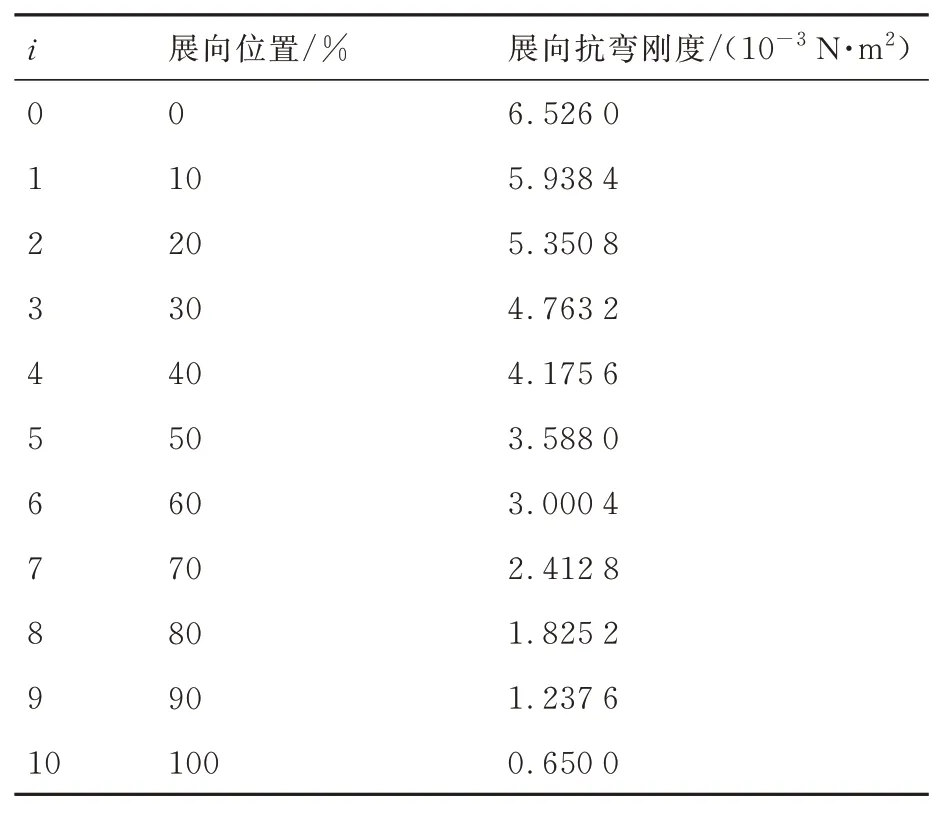
表10 扑翼沿展长的展向抗弯刚度Table 10 Bending stiffness along span of flapping wing

3.3.2 变截面扑翼参数优化

由于蜻蜓翅脉的截面尺寸从翅根到翅尖，从前缘到后缘都逐渐减小，且沿展长的抗弯刚度按线性函数减小，因此设扑翼脉络尺寸从翼根到翼尖，从前缘到后缘的变化也用线性函数描述。为了在满足扑翼刚度要求的同时使结构最轻，对扑翼进行优化设计，优化数学模型为

式中：lj=aj x+bj为各个梁的线宽函数，x为脉络延伸方向上某点的位置，aj为线性一次函数的斜率，bj为线性一次函数的截距；Ii为扑翼展长i×10%处的截面惯性矩（i取0，1，…，10）；j为第j条脉络；W为扑翼模型的质量；lmin和lmax为表示线宽的上下边界。

基于式（16）以扑翼质量最小为优化目标，各梁线宽函数的参数为变量，以表10 所示各展长处的刚度相似性和变量的上下边界为约束条件，采用序列二次规划方法和Matlab 中的Fmincon 工具箱对图9 所示的仿生扑翼各条脉络尺寸进行多次优化计算，并取每次优化结果平均值获得最终结果。图10 所示为优化过程的迭代收敛曲线，在迭代次数达到约为15 次时，目标函数值开始收敛到接近一个常数（扑翼质量约为1.1 g）。

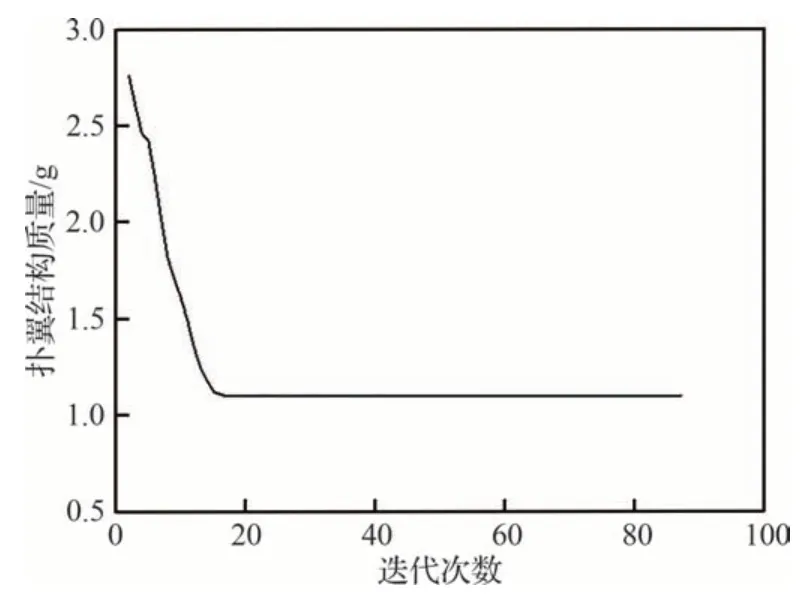
图10 扑翼质量在优化过程中的迭代收敛结果Fig.10 Iterative convergence results of flapping wing mass in optimization process

根据优化结果得到7 条脉络梁的线宽函数中的参数aj和bj，如表11 所示。根据表11 中的线宽函数参数aj和bj的优化结果可以确定扑翼模型中7 条脉络的线宽，线宽沿展向变化的结果如图11 所示，结合图12 所示的仿生扑翼模型的脉络分布可见，扑翼各脉络梁的线宽由翼根到末端、从前缘到后缘逐渐减小，脉络l1和脉络l3所处位置对应蜻蜓翅翼的前缘脉和径脉，由于前缘脉和径脉是蜻蜓翅翼中承力的主要构件，因此对于设计的扑翼这2 处梁的尺寸较大，符合自然界中飞行生物翅翼的结构特点。

图11 扑翼各脉络线宽优化结果Fig.11 Optimal results of flapping wing choroids width

图12 基于几何和刚度相似性的扑翼优化模型Fig.12 Optimized flapping wing model based on geometry and stiffness similarity

表11 扑翼模型部分梁线宽函数的参数Table 11 Parameters of partial beam line-width function of flapping wing model

虽然上述刚度相似性是基于第2 节中昆虫翅的展向刚度测量值获得的，但基于蜻蜓翅脉的分布对仿生扑翼开展的结构拓扑和优化结果也部分包括了弦向刚度的相似性。前期对相近尺寸的扑旋翼的展向和弦向刚度与升力关系的试验研究结果表明［29］，在展向刚度不变的情况下，扑旋翼的平均升力随着弦向刚度的增加而增加，例如展向刚度与弦向刚度比值为30，对应的升力为35.7 gf；当展向与弦向刚度比值减小到12 时，平均升力提高36%。随着弦向刚度增加或随着展向刚度与弦向刚度的比值减小，平均升力呈继续增大的趋势。表11 和图11 所示的结果表明，优化的仿生扑翼的展向和弦向刚度比小于12，例如在70% 展长与弦长处的展向刚度（2.418×103N·mm2）和弦向刚度（6.786×102N·mm2）比值大致为4，符合升力随弦向刚度增加的趋势。由于扑旋翼的最优弦向刚度与拍动升力和旋转推力的比例相关，换言之，最优弦向刚度需根据一个扑旋翼的设计目标是最大升力还是最大效率而决定。

4 实验与结果

4.1 升力测试实验

4.1.1 扑翼升力测试系统

采用课题组研制出的微型扑旋翼飞行器作为实物测试模型，轴对称安装在模型两侧的扑翼通过齿轮和连杆传动机构在电机的驱动下实现上下拍动，在拍动过程中产生方向相反的推力使扑翼同时绕中心轴产生旋转运动。模型试验测试平台由压力传感器、信号放大器、直流电源、NI数字采集系统、固定夹具、计算机组成，测试平台原理示意图及实物图分别如图13 和图14所示。

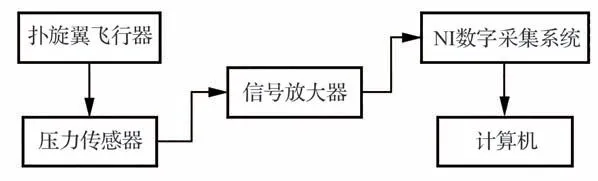
图13 升力测试系统平台示意图Fig.13 Schematic diagram of lift test platform

图14 扑旋翼升力测试系统实验平台Fig.14 Experimental platform of flapping wing rotor lift test system

由夹具固定在压力传感器上方的扑旋翼模型在试验中将沿竖直方向上产生的力传输至压力传感器（SKU-314990000），压力传感器将力信号转换为电信号且传输至信号放大器（RWST01A）放大并由NI 数字采集卡（NI USB-6009，采样率1 000 Hz）采集数据，最后传输至计算机对数据进行处理与存储。

升力测试实验流程包括：① 扑翼称重；② 传感器标定；③ 扑旋翼实验样机组装；④ 升力实验数据测试；⑤ 升力实验数据与结果分析。

4.1.2 扑翼模型制作

扑翼由骨架和翼膜组成，其中骨架按照图9和图12 的设计结果采用碳纤维板机加切割制成，翼膜选择厚度为0.015 mm 的聚酰亚胺薄膜，通过胶水粘连到扑翼骨架上。将图15（a）所示基于几何相似性设计制作的扑翼命名为JH 翼，图15（b）所示兼顾几何和刚度相似性制作的扑翼命名为GD 翼。

图15 仿蜻蜓扑翼实验样件Fig.15 Test samples of dragonfly flapping wing test

为了将仿生扑翼与目前扑翼飞行器研究中通常采用的矩形扑翼进行对比，设计制作了一对矩形扑翼。矩形扑翼的面积和展弦比与仿生扑翼一致，骨架由主梁、次梁和斜次梁构成，如图16（a）所示。由表10 可知，刚度沿展向线性变化，于是设置翼根处与70%展长处的刚度与仿生扑翼相同并满足表10 中刚度要求。各梁具体尺寸见表12。矩形扑翼的骨架采用碳纤维杆制成，翼膜采用与仿生扑翼相同的薄膜，通过胶水粘接得到如图16（b）所示的试验件实物，将该矩形翼试验件命名为JX 翼。

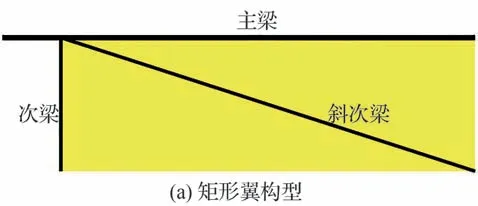
图16 矩形扑翼实验模型Fig.16 Test sample of rectangular flapping wing

表12 矩形翼模型的各梁尺寸Table 12 Dimensions of each beam of rectangular flapping wing model

4.2 升力实验结果与分析

4.2.1 GD 翼升力随电压的变化

为明确GD 翼在不同电压下的升力表现，进行了不同电压下GD 翼的升力测试研究，表13和图17 为实验得到的GD 翼的升力测试数据及变化规律。实验结果表明，GD 翼的升力随着电压增加而提高。当电压较低时，最大升力和最大负升力的数值比较接近，随着电压的升高，最大升力的增长趋势较快，最大负升力的增长趋势相对较缓，导致平均升力增加。这是由于GD 翼刚度沿展向减小，随着电压和频率的提高，扑翼在气动力作用下发生扭转，减小了上拍过程中产生的负升力，符合自然界中昆虫的运动方式。在电压为3.4 V 时升力达到了14.7 gf，接近文中用于试验的仿生扑旋翼模型的重量，可实现垂直起飞。

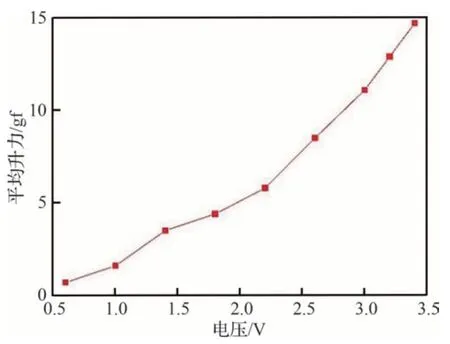
图17 GD 翼平均升力随电压变化结果Fig.17 Increase of average lift with input voltage

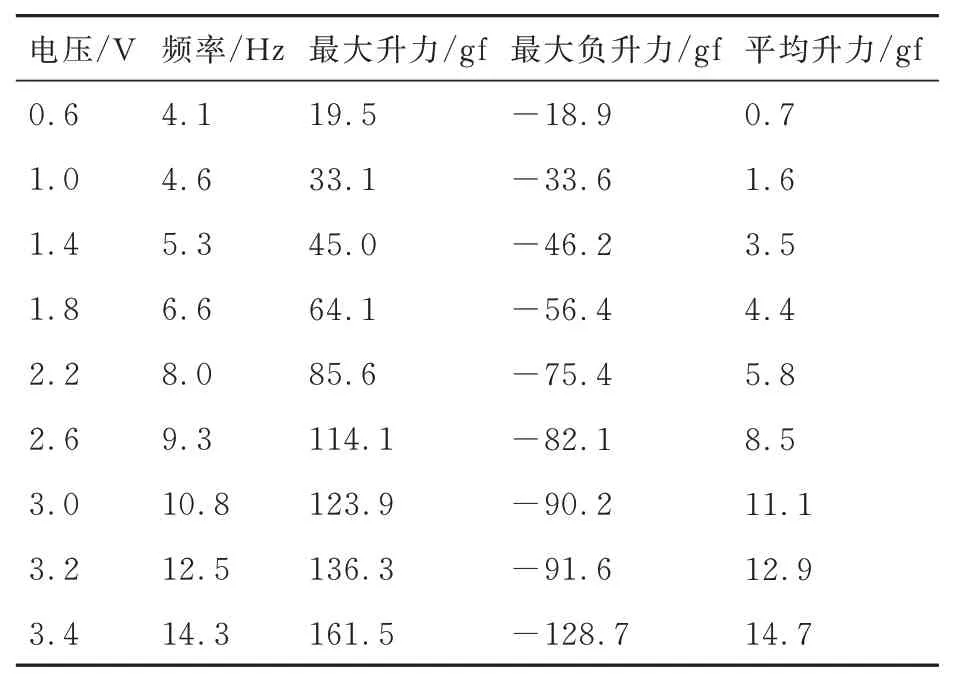
表13 不同电压下GD 翼升力测试结果Table 13 Results of lift of GD wing at different voltages

4.2.2 GD 翼与JH 翼的升力对比实验

为了探究扑翼刚度对升力的影响，将JH 翼的升力测试结果与表13 的GD 翼升力结果进行对比。由于JH 翼仅根据几何相似性设计制作而成，忽略了刚度相似性准则，且刚度相对小，为获得稳定的测试数据，将试验的拍动频率定义在较低范围进行。JH 翼在不同拍动频率下的升力测试结果如表14 所示，二者在不同拍动频率下的升力变化情况如图18 所示。

图18 GD 和JH 翼在不同拍动频率时产生的平均升力Fig.18 Average lift of GD wing and JH wing at different flapping frequency

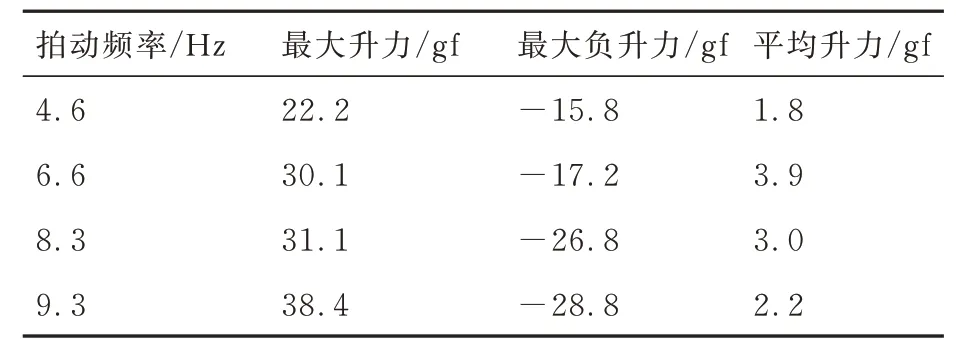
表14 JH 翼升力测试结果Table 14 Test results of lift from JH wing

由图18 可知，GD 翼的平均升力在4.5～9.5 Hz 的低频拍动范围内随拍动频率的提高呈线性增加，与之不同，JH 翼的平均升力在4.5～6.6 Hz 低频拍动时随拍动频率呈线性提高，且与GD 翼的结果接近，但在高于6.6 Hz 的拍动频率时升力急剧下降，这是因为JH 翼的刚度偏小，其弹性变形随着拍动频率和相应的惯性力和气动力的提高而超出了承受范围。由表14 可见，尽管JH 翼在9.3 Hz 拍动频率时产生的正负力峰值均大于6.6 Hz 时的结果，但得到的平均升力却明显减小，而基于几何和刚度相似性设计的GD 扑翼所产生的升力比仅基于几何相似性设计的JH 扑翼高出2 倍以上（表15）。

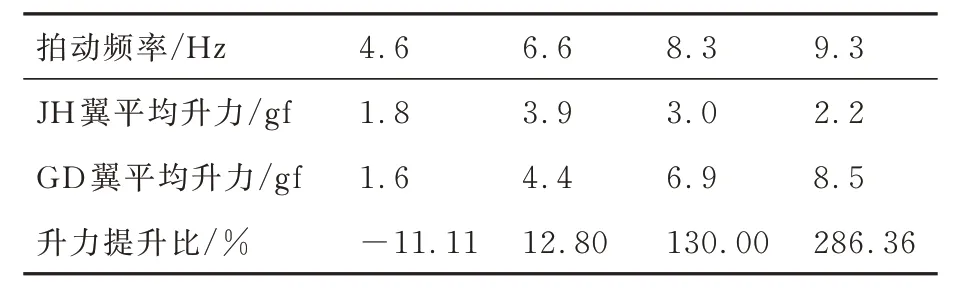
表15 不同拍动频率下GD 翼与JH 翼的平均升力及提升比Table 15 Average lift and increasing ratio of GD wing and JH wing at different flapping frequency

4.2.3 GD 翼与JX 翼的升力对比实验

明确了兼顾几何和刚度相似性的GD 翼升力特性优于仅考虑几何相似性的JH 翼，为了进一步验证仿生扑翼形状和结构对提高升力的影响，采用前文设计制作的JX 翼进一步开展了实验研究，对比GD 翼与JX 翼在试验条件下的升力表现。表16 为JX 翼的升力测试结果，GD 翼和JX翼平均升力的变化情况如图19 所示。

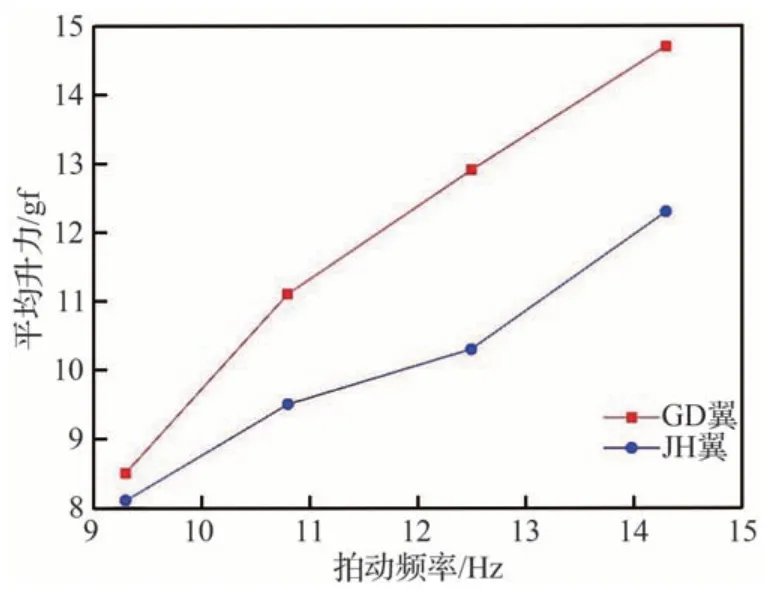
图19 GD 翼和JX 翼在不同拍动频率时产生的平均升力Fig.19 Average lift of GD wing and JX wing at different flapping frequency

表16 JX 翼升力测试结果Table 16 Test results of lift from JX wing

由图19 可知，GD 翼和JX 翼的平均升力随着拍动频率的增加都以近似线性变化增加。GD翼的平均升力显著高于JX 翼，且由表17 可知，在12.5 Hz 的拍动频率时比JX 翼的平均升力提高了25.2%，说明仿生扑翼形状与结构对扑旋翼的气动力起到了有效的增升作用。但本研究限于气动模拟方法对几何外形进行优化，仅限于与传统矩形翼为初始设计开展刚度相似性的研究，所以不能对该仿蜻蜓翅几何外形即为最优外形下结论。

表17 不同拍动频率下GD 翼与JX 翼的平均升力及提升比Table 17 Average lift and increasing ratio of GD wing and JX wing at different flapping frequency

5 结 论

基于主成分分析法获得的昆虫翅几何参数与抗弯刚度的关系，通过蜻蜓翅的刚度实验数据可建立用于仿生扑翼设计的刚度相似性准则。基于拓扑方法和几何相似性设计制作了仿蜻蜓JH 扑翼，进而采用刚度相似性准则确定仿蜻蜓JH 翼的结构参数，设计制作了GD 扑翼。为了深入对比分析，仅基于刚度相似性设计制作了普遍采用的由主次梁构成的矩形JX 扑翼。最后通过扑旋翼模型试验测试了3 种扑翼的升力表现，结果对比验证了仿蜻蜓GD 翼具有显著的气动力增升效果，并得到如下结论：

1） 昆虫翅脉结构分布和几何相似性可作为仿生扑翼设计的必要条件，但不是充分条件。因为结构刚度不足的扑翼产生的升力仅在低频拍动时随频率提高而线性增加，但升力也偏小；当拍动频率提高到一定值后（JH 翼大于6.6 Hz），升力反而随频率的提高而明显下降。换言之，扑翼的刚度应根据飞行器设计的升力要求而定。

2） 基于昆虫翅的刚度相似性也可作为仿生扑翼设计的必要条件，但仍不充分。如采用通常的矩形扑翼简化结构，基于刚度相似性确定其主次梁参数后制作的JX 翼，在拍动频率为9.3 Hz时产生的升力是仅基于几何相似性设计的JH 翼的4 倍。虽然JX 翼相比JH 翼在拍动频率和升力上都可成倍提高，但仍不够理想，这也是迄今为止仿生扑翼优化面临的问题。

3） 将昆虫翅脉分布几何相似性和结构刚度相似性相结合的准则可作为仿生扑翼设计的必要和充分条件。试验结果表明，基于这一准则设计制作的GD 扑翼在5～15 Hz 拍动频率范围内测试的升力都明显优于仅基于几何相似性或刚度相似性的JH 翼和JX 翼。例如，在拍动频率12.5 Hz 时GD 翼产生的平均升力比矩形JX 翼提高了25.2%，即在满足仿生几何外形和仿生翅刚度相似性的条件下GD 翼是最优设计。

4） 实验验证了扑旋翼结构和刚度以及仿生扑翼形状对升力有显著的影响，根据几何和刚度相似性制作GD 翼产生的升力随输入电压的提高而增加，在电压达到3.4 V 时产生的升力达到14.7 gf，接近用于试验的仿生扑旋翼模型的重量，可实现垂直起飞。